Niederbayern88 schrieb:Ich habe wohl vergessen, dass die Mandelbrotmenge etwas mit der Chaostheorie zu tun hat. Je Tiefer man also in ein Fraktal eindringt, umso verwirrender scheint alles. Dass es eine gewisse Ordnung gibt, will ich jetzt weder befürworten noch verneinen.
Dahingehend kommt mir auch die Erinnerung an ein Video über Primzahlen, was ich vor gar nicht allzu langer Zeit auf Youtube fand.
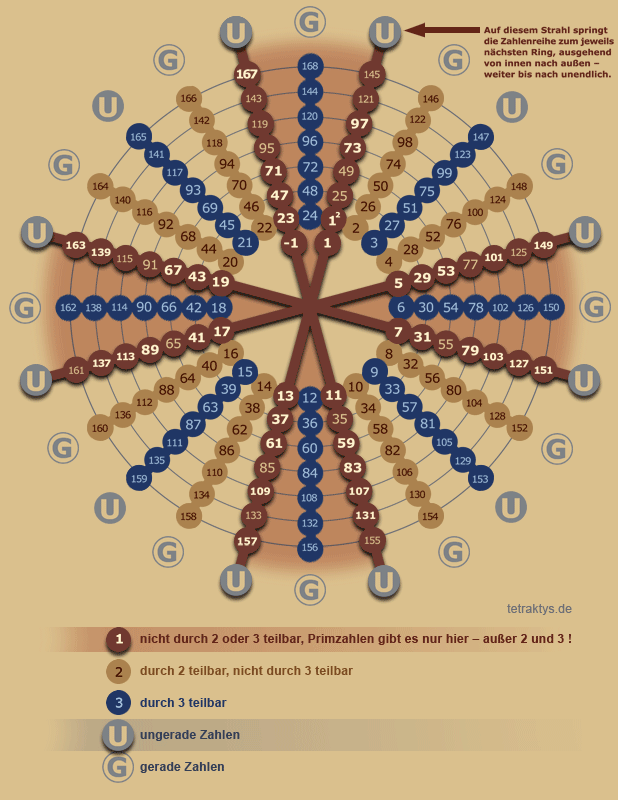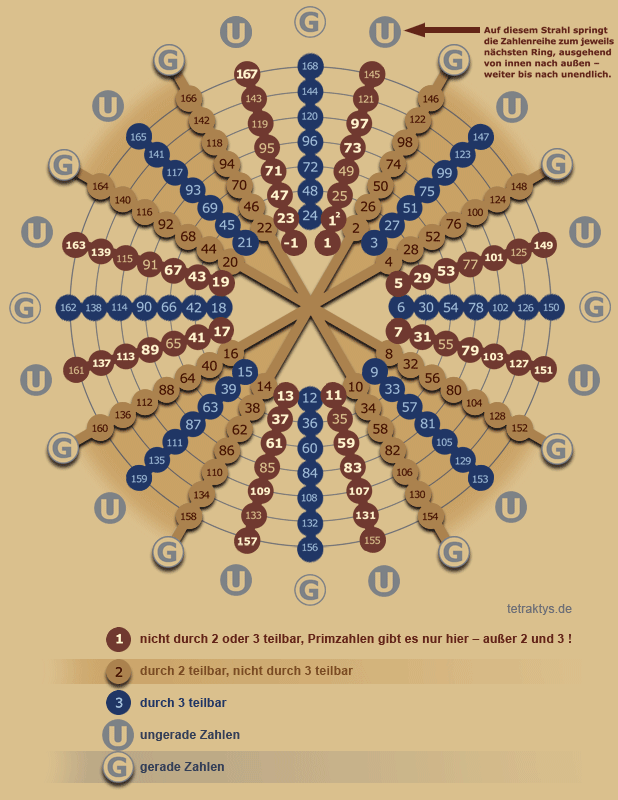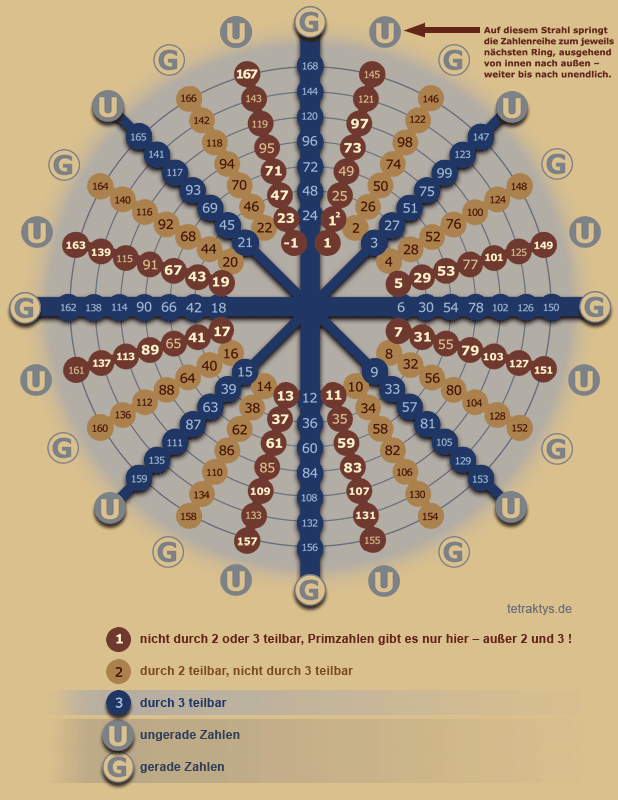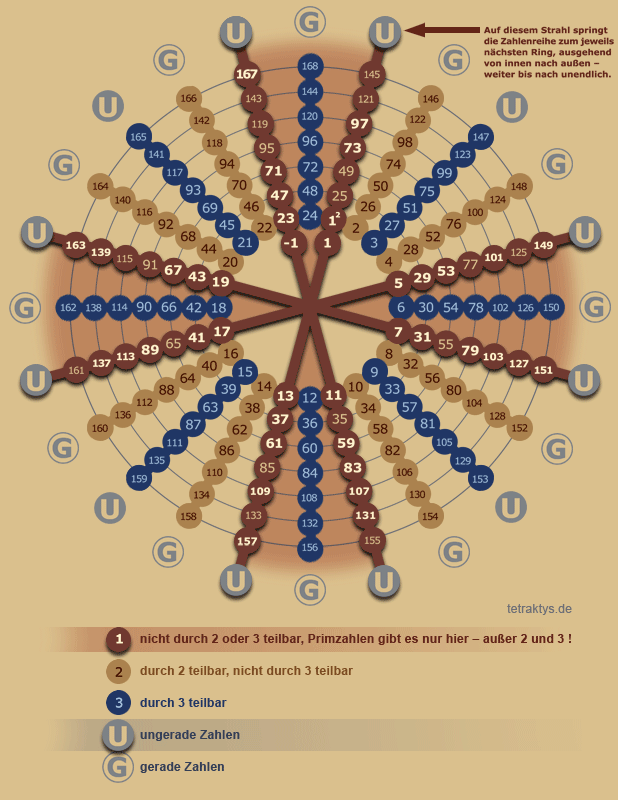
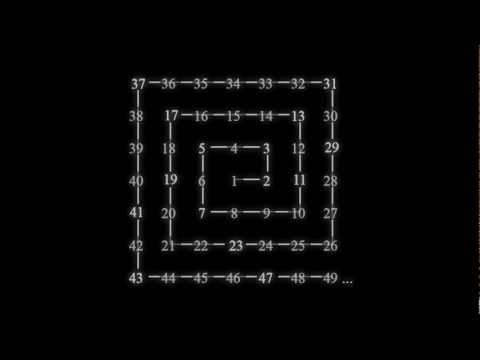
Dabei ging es darum die natürlichen Zahlen in einer Art eckigen Spirale nacheinander anzuordnen und dann den Primzahlen bezüglich einer gewissen Eigenschaft einen Kreis zuzuordnen.
Könnte sein, dass dabei der ganzzahlige Rest der modulo 2 Division als Radius hergenommen wurde, ich weis es aber ehrlich gesagt einfach nicht mehr, nach welchem Kriterium die Radien für die Kreise gewählt wurden.
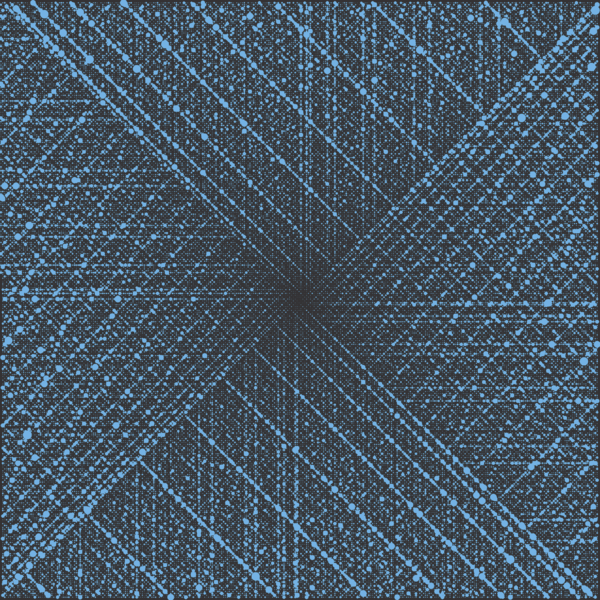
Letztlich lief es aber darauf hinaus, dass man dies mit einer großen Menge durchführte und nach dem entsprechenden Muster diese Kreise einzeichnete und dann einmal herauszoomte.
Dabei entstand ein Muster, bei dem man von der Ferne das Gefühl bekam, dass da im Großen und Ganzen doch kein allzu schlimmes Durcheinander vorherrschen könnte.
Mir persönlich kam dann noch die Erinnerung an die Jahre in denen ich mit dem Programm Apophysis gearbeitet hatte, weil das im Video gezeigte Muster eines war, das zumindest von der Ferne wie etwas aussah, was man auch mit wenigen Handgriffen über ein solches iteriertes Funktionensystem erstellen konnte - zumindest schematisch.
Letztlich kommt bei Primzahlen ja auch "nur" die Frage auf, ob eine natürliche Zahl eben die Primzahleigenschaft hat oder nicht. Was so gesehen auch nichts anderes ist als eine Gruppe von Studenten im Hörsaal nach ihrer Augenfarbe zu fragen.
Es ist zwar auch wieder nur mehr Spekulation als alles andere, aber da die Primzahlen eben doch momentan in Ansätzen doch so etwas wie Regelmäßigkeiten aufzeigen, könnte man vielleicht auch da mit Algorithmen, die es noch gar nicht gibt, Muster von Selbstähnlichkeiten finden.
Alles in allem ist die Geschichte der moderneren Mathematik noch gar nicht so alt.
Nicht nur was den noch jungen Bereich der Rechenwerke bzw. Computer angeht, so findet man in nahezu jedem mathematischen Bereich etwas, was wir heute fast als selbstverständlich verstehen, was aber gleichzeitig erst innerhalb der 100-150 Jahre ordentlich ausgearbeitet wurde.
Und gerade der Bereich der Faktalen Geometrie hat erst durch die modernen Rechenwerke überhaupt wieder Beachtung gefunden.
Ich bin wirklich gespannt, was da die nächsten 50 Jahre noch bringen werden.
