Das selbst-identische Universum

@fritzchen1

Ich weiß doch das wir da schon bei sind. :)

Macht das Ganze dann aber auch nicht Verständlicher.

Oder vielleicht doch?!?
Da bin ich mir jetzt auch nicht einig. :D


Gruß
Mailo

Jedenfalls ist ein Fraktal zumindest eine Möglichkeit sich diese Unendlichkeit in zwei Richtungen (eigentlich in alle), in den räumlichen und zeitlichen Dimensionen, wie auch im kleinen und großen vorstellbarer zu machen. Ich denke mal das wir in einem Multiversum existieren, jedoch sie die anderen Universen auch wieder nur Teil eines nächst größeren. Irgendwie so ähnlich:

The Simpsons[Homer's Head]

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Mailo schrieb:Macht das Ganze dann aber auch nicht Verständlicher.

Macht auch nichts, da heute völlig offen ist wo die Expansion in einem inflationären Universum noch enden soll.

@fritzchen1
Ja da bekommt man Kopfsurren von.

Auch wenn man bedenkt, das der Raum ja durch die Expansion erst entsteht.
Worin expandiert er dann?

Gruß
Mailo

Mailo schrieb:Worin expandiert er dann?

Um mich meinem Vorredner noch mal anzuschließen. In einem Denkenden Individuum und nicht wie das die Moderne Physik beschreibt.

https://www.youtube.com/watch?v=Lwbm-m3X_eg

@fritzchen1

In Homers Schädel.
Jo, da is auf jeden noch genug Platz für einige Universen. :D

Wir spammen.

Gruß
Mailo

https://dl.dropboxusercontent.com/u/24509641/Das%20selbst-identische%20Universum.pdf

Einfachheit im Ergebnis durch Komplexität am Boden

Die letzten Posts waren nicht unbedingt von Ernsthaftigkeit geprägt. Wir sind jetzt beim Thema des Threads angelangt und ich habe inzwischen damit begonnen, es zu umreißen. Mein Anliegen dabei ist es nicht, vielleicht eine Konfetti-Bombe für Neujahr vorzubereiten oder ein paar ulkige Raketen in den Himmel zu schießen. Ich werde im weiteren zu erklären versuchen, dass über mein Konzept der 3-dimensionalen "Anzeige-Tafel" durchaus plausibel dargestellt werden kann, was Raum tatsächlich sein könnte - was es mit den Wahrscheinlichkeiten in der Quantenphysik auf sich haben könnte - wie es zu unserem Bewusstsein kommen könnte und vieles mehr.

Ich wäre froh, wenn dazu die eine oder andere Bemerkung käme, Anregungen oder ernst-gemeinte Diskussionsbeiträge. Die letzten Posts sahen mir so ein wenig danach aus, als sähe man die Geschichte nur als einen zu spät gekommenen Geck für den 11.11.

SO ist es nicht gemeint! Ich will ernsthaft versuchen, an diesem bildhaften Denk-Modell darzulegen, dass man wieder zu intuitivem Verstehen zurückfinden kann. Der Preis dafür ist allerdings die ungeheure Komplexität, die ich am Boden des Modells ansetze.
In diesem geht es also nicht von unwissenden, nichts verstehenden, blinden und bewusstlosen Elementar-Teilchen in einer langen Entwicklung hinauf zur Geburt von Sternen, Planeten-Systemen, Leben und schließlich zum Erscheinen intelligenter Lebensformen. Vielmehr bündelt sich in meinem Bild alles zu einem einzigen Großen-Ganzen, in welchem vor dieser Entwicklung schon eine andere Entwicklung stand, die wahrscheinlich unermesslich viel länger dauerte - und es steht davor auch ein höheres Prinzip - es steht davor eine Leistungsfähigkeit, verglichen mit der unser kleines Bisschen menschliches Denken nur wie ein Staubfaden erscheint, der durch einen riesigen atmosphärischen Ozean getragen wird und in dem sich nur ein klein wenig das spiegelt, was das große Orchester des Seins erst ermöglicht.

Ich verwende nicht den Begriff "Gott" und werde das nie tun, weil ich weder mit Religion/en noch mit spirituellen Fragen oder mit Esoterik innerlich etwas zu tun habe. Ich bin am Problem interessiert, das ich sehe - an sonst überhaupt nichts. Und was ich an diesem Problem sehe, das dreht sich mehr oder weniger immer wieder um folgenden Kern:

Wer in seine Erklärungs-Ansätze aus Unwissenheit etwas Entscheidendes nicht einfließen lassen kann, der kann die Sache tausendfach wenden und wird doch niemals sehen, wie sie tatsächlich aussieht. Wer (vor der Zeit des Fernsehens) noch niemals z.B. in Indien war, mag sich die blumigsten Bilder zusammen-reimen. Wenn in seinen Phantasien aber etwas Grundlegendes fehlt, was für ein Verständnis unabdingbar ist, dann wird da nie ein Schuh draus aus dem, was er sich zusammen-reimt. Gerade vorhin habe ich Makro geschaut. Da erzählt ein Emirati: "Als ich ein kleiner Junge war, hat man mir erzählt, dass in Europa die Menschen völlig nackt herum-laufen und die Frauen vollkommen ohne Scham in der Öffentlichkeit geküsst werden"... Inzwischen ist er mit einer Engländerin verheiratet uns sie haben etliche Kinder zusammen.

Nun - und das, was in unseren Welt-Erklärungs-Modellen eventuell fehlt, das KANN man ja zunächst nur in einem spekulativen Denk-Ansatz voraus-ahnend zu skizzieren versuchen. So entstehen schließlich immer Hypothesen oder Theorien. Wir haben gewissermaßen immer schon die Ahnung des Ergebnisses in unserer These, noch bevor wir uns auf den Weg machen können, diese zu begründen - genau so wie der Komponist bereits die Ahnung einer gesamten Symphonie in sich trägt noch bevor er sich daran-macht, diese in einzelnen Noten zu festzuhalten.

Und ich sehe in meiner Ahnung eben, dass an unserer Sicht auf die Welt schlicht und ergreifend elementar etwas nicht stimmt. Sie steht für mich irgendwie auf dem Kopf. In dieser Haltung stehe ich nicht alleine. Es gibt unzählige Menschen, die alle auf ihre Art bereits versucht haben, diese Vor-Ahnung in ein Gesamt-Konzept einzubinden - wie eben auch Amit Goswhami, über den ein Video ja bereits auf der aller-ersten Seite dieses Threads verlinkt worden ist. Er sieht (im Ergebnis und in der Interpretation zwar anders als ich) vom Ansatz her genau das gleiche Problem:
Man kann sich dieses Sein nicht erklären, wenn es aus völlig Blindheit heraus gestartet sein sollte. Und wer dann um ein tieferes Verständnis ehrlich bemüht ist, der sagt das nicht nur. Er versucht plausibel zu machen, wie er auf seine Gedanken kommt - oder wie er sich das "Getriebe der Welt" vorstellt: Ich habe ein Gedanken-Modell, anhand dessen ich (natürlich zunächst einmal nur mir selbst) vor Augen zu führen versuche, wie es nicht nur sein, sondern auch wie es funktionieren könnte.

Deshalb hoffe ich und setze sehr darauf, dass unter den ja ohnehin sehr wenigen Teilnehmern an diesem Thread ab jetzt (so wie zu Beginn und bis vor kurzem) auch wieder einige sein werden, die an ernsthaften Betrachtungen interessiert sind - die sich ernsthaft beteiligen möchten - die ein Gespräch bereichern und es nicht nur mit Albereien total verwässern möchten.
Bitte nicht missverstehen: Humor, Witze, ironische Bemerkungen usw. usf.: Alles herzlich gerne! Nur eben nach Möglichkeit nicht die schiere Alberei und nur noch Blödelkram. Die letzten Posts gingen leider so ein wenig in diese Richtung, was zum Schluss auch eingeräumt worden ist.
Daher nochmals: Ich möchte wirklich in ernsthafter und in tief-gehender Auseinandersetzung mit dem Thema darzustellen versuchen, wie es sein könnte - bzw. wie es AUCH sein könnte (wenn man es so lieber hört - wie man es gerade haben möchte).
Ich bin aber hier nicht dabei, einen Sketch zu schreiben, damit ich zu Silvester von Dieter Nuhr eingeladen werde, um meine Gedanken unter "Nuhr Selbst-Identisches" dann neben ihm auf der Bühne zum Besten geben zu dürfen!

So - nach dieser Zwischenrede werde ich mich wieder dem Thema zuwenden und es immer weiter ins Detail hinein langsam ausbreiten.

sunaJJanus schrieb: Die letzten Posts sahen mir so ein wenig danach aus, als sähe man die Geschichte nur als einen zu spät gekommenen Geck für den 11.11.

Das is ma bitter.

:/

Einfachheit im Ergebnis durch Komplexität am Boden

Das "Nicht-zu-fassen-Kriegen" MÜSSEN wir uns jetzt unbedingt tiefer vornehmen - auch wenn schon das von mir bis hier-her Gesagte bei Vielen, die in die Thematik einmal kurz hinein-geschnuppert haben, schon dazu geführt haben mag, sich so rasch auch wieder abzuwenden, wie dieser kurze Schnupper-Moment währte.

Ein Teil unserer Gesellschaft ist immer noch im Sinne der von Peter Scholl-Latour definierten Spaß-Gesellschaft zu verstehen: "Events" (ganz gleich ob nun tatsächlich im reinen Unterhaltungsbereich oder eher im Bildungs-Sektor angesiedelt), werden vornehmlich im Hinblick auf ihre zeitlich eng begrenzte Brauchbarkeit im HIER und HEUTE (vielleicht noch ein weeenig darüber hinaus) "ab-gecheckt" - und wer es sich eben leisten kann, der checkt diese Brauchbarkeit nur noch unter einem einzigen Aspekt ab: Dem "Spaß-Faktor".
Jeder hat da so sein eigenes Maß in sich, das durchaus der Zuschauer-Quote vergleichbar ist: Es muss ein bestimmter "Spannungs-Wert" erreicht werden: Wird er überschritten, dann hält mich "das Dingens" - es "fesselt mich". Der Wert wird aber fort-dauernd weiter-gecheckt: Und sowie der "Quoten-Wert" deutlich unterschritten wird, zappt man dann weiter - im ewigen Fluss und bei der fortdauernden Suche nach neuen, ausreichend hohen "Spannungs-Werten":

Aber ich lese mal weiter mit, und schau dann mal, wo Du diesen Fred hinsteuern möchtest oder kannst.
Hast im Eingangspost ja auch ordendlich Spannung aufzubauen versucht. :popcorn:

Sagt eigentlich alles (auch das Popcorn ist von Bedeutung!) - muss nur ein klein wenig umgedeutet werden:

Ich habe am Anfang nichts anderes versucht, als mich dem Thema langsam zu nähern. Ich hab auf das Erzeugen von Spannung gar nicht geachtet. Aber bei dem Interpreter hat der "Quoten-Zeiger" ausgeschlagen, weil BEI IHM offensichtlich ein Spannungs-Wert überschritten worden ist und somit sein Interesse geweckt war.

Bei weiteren Bemerkungen wird es dann allerdings hoch-interessant - JETZT für mich! Nun wurde bei mir ein "Interessens-Wert" überschritten, der bei mir anzeigt:

"Mann - das passt ja hervorragend - das lässt sich ja fast ideal in das einbinden, was es zu erklären gilt."

Chronologische Reihenfolge: ohne Gewähr! :

Jo, instandvideos die sind geil..

Wenn wir dann die Zeit noch Hypnosaften wird Es noch verwirrender.

Alles ist nur im Wandel, da kommt nichts dazu ud geht auch nichts Verloren.

Muss ich jetzt was schlaues schreiben?
Dann vielleicht sowas:
Ein Eindruck ist nur das Resultat von Etwas erlebtem. Der Eindruck selbst sagt nur sehr wenig über das Etwas aus.

Zusammen-genommen entsteht ein bestimmter EINDRUCK (siehe letztes Zitat !).
Und nun ginge es ÜBER den Eindruck zum Problem, sich VERMITTELS dieses Eindrucks ein Bild von diesem "Etwas" machen zu sollen (zu dürfen / zu können).

Im Grunde genommen nimmt der Zitierte (oder DAS zitierte "Etwas") die Antwort bereits vorweg:

Der Eindruck selbst sagt nur sehr wenig über das Etwas (den Zitierten) aus.

Das stellt sich folgendermaßen dar:

1: Der geschriebene Spruch IST ein schlauer Spruch: TRUE !
2: Der geschriebene Spruch hinterlässt einen Eindruck über den geschriebenen Spruch
3: Der geschriebene Spruch hinterlässt einen Eindruck über den Schreiber.

Frage: Korrelation zwischen Schreiber und geschriebenem Spruch ?

Antwort: Aus dem Schreiben eines schlauen Spruches darf auf die Schlauheit des Schreibers geschlossen werden: FALSE !


Es besteht die Möglichkeit, dass dieses Etwas (des Schreibers) aus sehr vielen und auch aus sehr vielen komplexen und hoch-strukturierten Informationen bestehen könnte.
Nennen wir das die Möglichkeit A - und setzen wir A einmal mit Schlauheit gleich.
Weiter gibt es die Möglichkeit, dass dieses Etwas (des Schreibers) aus sehr wenigen und auch aus sehr wenig komplex strukturierten Informationen bestehen könnte.
Nennen wir das die Möglichkeit B - und setzen wir B einmal mit Debilität gleich.
Schließlich gibt es alle noch erdenklichen Übergänge zwischen A und B.

Der Schreiber könnte also intelligent sein bis dumm wie Brot in allen Übergängen.

AAAABER:

WIE wir ein "Etwas" erleben, das prägt im naiv-realistischen Verständnis-Modell fortwährend unser SAGEN !
Fortwährend machen wir Aus-Sagen über Etwas, was wir erleben - MEINEN dabei aber nicht nur eine Aussage zu machen über unseren Eindruck, sondern über das Etwas selbst, das wir erlebt haben.

Wenn wir also etwa über unser Auto reden, so glauben wir, dabei über DAS Auto zu reden, was "draußen in der Welt vor unserer Garage steht". Wir sagen aber in Wahrheit nur etwas über die Eindrücke aus, die dieses Auto "dort draußen" in uns hinterlassen hat.

Dass wir nicht über das Auto "in seiner Gesamtheit" reden - dass wir nicht von einem Ding oder einem Etwas reden, das wir mit unserem SAGEN (mit unseren Beschreibungen) all-umfassend wiedergeben könnten:

Das ist eigentlich JEDEM von uns klar. Aber auf eine etwas "schwammige" Art.

Warum?

Weil wir als Menschen einen "Mechanismus" in uns tragen, der sich "Identifikation" nennt und der es uns erlaubt, Wissen, das wir selbst nicht haben, dennoch als uns selbst gegeben voraus-setzen zu dürfen:
Es ist zwar nur extern vorhanden. Aber wenn mein Auto kaputt geht und ich einen Mechaniker brauche, weil ich selbst nun nicht mehr weiter-komme mit dem Bild, das ICH von Autos habe, dann weiß ich den Weg zu diesem Auto-Mechatroniker:
Das erweiterte Mechatroniker-Wissen ist zwar MIR verborgen - es ist aber dennoch PRINZIPIELL ZUGÄNGLICH !

Ergo glauben wir, die Gleich-Setzung des Bildes, das ich von meinem Auto habe mit dem Auto selbst SEI EBEN DOCH STATTHAFT (was es in Grenzen eben auch ist).

Kommen wir nun aber zu der Frage, wie die Dinge liegen, wenn dieses "Etwas" ein Mensch ist.

Ist es dort genau so statthaft, den Eindruck, den ich von DIESEM Etwas (dem Menschen) gewinne, gleich-zu-setzen mit diesem Etwas selbst? Wieder weil ich davon ausgehe, dass zwar MIR nicht alle Informationen zugänglich seien, wodurch dieser Mensch gekennzeichnet wäre. Der Menschheit insgesamt seien sie aber zugänglich?

Nun - hier kommen wir also bei tieferen Fragen an, die der naive Realismus aufwirft.

Zuvor aber zu einer hier ebenfalls notwendig werdenden Unterscheidung:

NAIV versus NAIVER REALIST

Ein Mensch, der nach obigem Beispiel den Sprecher eines schlauen Spruches GLEICH-SETZT mit einem schlauen Menschen ist naiv.

Ein Mensch, der dies NICHT tut aber gemäß des anschließend beschriebenen Identifikations-Prinzips davon ausgeht, dass die Schlauheit eines Menschen prinzipiell messbar sei, der ist in ziemlich exakt DEM Maße ein naiver Realist, in dem er hier von einer exakten Bestimmbarkeit ausgeht.

Naiver Realismus als Phänomen ist also relativ einfach fassbar:
Je genauer ein Mensch glaubt Bescheid zu wissen, wenn er sich zu Fragen äußert, die ER SELBST nicht genau bestimmen kann, je stärker ist er einem naiven Realismus verhaftet.

Und nun werfen wir die Frage auf, ob eine Ermittlung der Schlauheit des Schreibers möglich wäre:

Wir stoßen darüber auf das PRINZIPIELLE Problem, dass wir in der Analyse eines "Etwas" als Menschheit zwar immer weiter voran-schreiten. Uns offenbart sich JETZT aber ein Circulus Vitiosus:

JA - wir steigen zwar immer tiefer und immer tiefer in unseren Betrachtungen und gewinnen dabei immer mehr und immer mehr Eindrücke von einem "Etwas" - von einem Gegenstand unserer Betrachtung.

GRUNDSÄTZLICH kommen wir aus dieser Nummer aber nicht heraus!

IMMER beschreiben wir nur die Eindrücke, die wir gewinnen - und NIEMALS dieses Etwas selbst, welches in uns die Eindrücke hinterlässt!

Ich hoffe, damit habe ich die Grundlagen des Konstruktivismus leidlich verständlich und einigermaßen nachvollziehbar umrissen. Wer dort nachlesen möchte, findet einen Link zum radikalen Konstruktivismus (den auch ich selbst unter gewissem Vorbehalt sehe).

Einfacher verständlich wird es noch, wenn wir uns vor Augen halten, dass wir IMMER nur auf "Oberflächen" schauen. Der Begriff "Oberfläche" muss nur ein wenig modifiziert werden.

Selbstverständlich kann ich die Dinge "aufbrechen" und tiefer in sie hinein-schauen.
Generalisiert im Sinne eines Prinzips gilt aber, dass wir beim Tiefer-Steigen IMMER nur von Oberfläche zu Oberfläche gehen - NIEMALS aber ins "INNERE des Etwas" schauen können, das in uns einen Eindruck hinterlässt.

Mit noch so vielen Oberflächen gelingt es aber NICHT, dieses "Etwas" all-umfassend-all-umfänglich zu erfassen! Und das Holographische Prinzip hat daraus kurzer-hand einen umgekehrten Schuh gemacht:

ES GIBT überhaupt nur Oberflächen! Wahrnehmungen in höheren Dimensionen des Raumes und der Zeit sind Illusion.
Na, na, na....

Ich drehe es also wieder herum und rücke es zurecht:

Das holographische Prinzip ist in dieser Weise eine Fehl-Interpretation.

Es sagt nichts anderes aus, als dass Information in dem Maße mehr und immer mehr RAUM (Leere um sich herum) braucht, in dem sie sich HÖHER STRUKTURIERT.

Das Schloss des Königs im Vergleich zur kleinen Hütte des Waldarbeiters bietet eine wunderschöne Metapher!
Und jetzt heißt es: Junge Geister dieser Welt: Macht euch daran, diese Relation irgendwie wissenschaftlich zu fassen zu kriegen!

Wieso hängt das RAUM-GREIFEN komplexer werdender uns sich höher strukturierender Information mit EBEN diesem neuen Paradigma zusammen?
Wieso ist es gerade DIESE Relation, die wir da gefunden haben?
Weshalb müssen die "Paläste" unserer Welt um eben ein Maß größer werden, das in einem Verhältnis steht zu der sie umhüllenden Fläche, wenn die Information, die sie bergen, nicht nur MEHR ist, sondern auch komplexer und höher strukturiert vorliegt (nehme man irgend-einen Konzern - eine Bank - eine Handelskette)?
Warum fällt der REALTIVE Raumbedarf ergo gerade SO aus bei immer höherer Strukturierung?
Warum muss ein doppelt so komplexer Konzern, der auch doppelt so strukturiert organisiert ist und mit (rein quantitativ) doppelt so großen "Informations-Mengen" umgeht, nicht ein Warenlager bauen, das doppelt so viel Volumen enthält?

Eine aller-erste Vor-Ahnung könnte man haben: Schaue man sich etwa das
"Just-in-time-Management"
der modernsten Betriebe an! Das spart ungeheuer viel Lagerkapazität ein, die man sonst vorhalten müsste.

Und NOCH EINMAL zum Holographischen Prinzip

Ich werde mir damit selbst untreu, weil ich mich eigentlich schon von diesem Thema verabschiedet habe. Aber es hat mich ein wenig am Wickel - es fasziniert. Jeder, der sich damit beschäftigt und einen "Touch" davon kriegt, wird vielleicht in gleicher Weise "affiziert"... Susskind betonte auf vielen seiner Vorträge und in Vorlesungen immer wieder, dass er im Holographischen Prinzip eines oder DAS tiefste Prinzip sieht, das in der Natur waltet. Er sieht es in Zusammenhang mit dem Energieerhaltungssatz und den 4 Hauptsätzen der Thermodynamik und nennt es deshalb auch manchmal "Das minus-Erste-Gesetz".

1. - 1. (minus erster) Hauptsatz: Bekenstein-Grenze :
Entspricht der Entropie in einem sphärischen Raumbereich mit bestimmter Oberfläche A (der Oberfläche beim Schwarzschild-Radius / Event-Horizon). Es ist die Entropie, die in einem Schwarzen Loch dieser Größe enthalten ist. Da die Größe eines Schwarzen Loches proportional zu seiner Masse ist, ist die Informationsmenge, die in einer Raumsphäre enthalten sein kann, proportional zum Quadrat der enthaltenen Masse und damit proportional zur Oberfläche A.

0. Hauptsatz: Einführung der Temperatur als physikalische Grundgröße:
Stehen zwei Systeme jeweils mit einem dritten im thermodynamischen Gleichgewicht, so stehen sie auch untereinander im Gleichgewicht. Diejenige Zustandsgröße, die bei diesen Systemen übereinstimmt, ist die Temperatur.
1. Hauptsatz: Die Energie eines abgeschlossenen Systems ist konstant.
2. Hauptsatz: Thermische Energie ist nicht in beliebigem Maße in andere Energiearten umwandelbar.
3. Hauptsatz: Der absolute Nullpunkt der Temperatur ist unerreichbar.

Die Formulierung des Holographischen Prinzips aus der Bekenstein-Grenze ist allerdings bei genauem Hinsehen eine seltsam bleibende Verknüpfung des bereits Bekannten unter Einbeziehung der Quantenphysik und der Relativitätstheorie.
Ganz wesentlich dabei ist die Überlegung, dass ein und der-selbe Vorgang, nämlich das Hinein-Fallen in ein Schwarzes Loch, EINMAL von außen betrachtet und einmal aus der Perspektive des Hinein-Fallenden selbst, kommutativ sei. Dabei geht es letztlich um Relativitätstheorie - die "Bilder" des Außenstehenden Beobachters, der ein Rauschiff sieht, das spagettisiert und zerrissen wird und das Bild das sich ein Besatzungs-Mitglied macht, müssen "gleichberechtigt" sein und in einer Transformation in-einander zu überführen sein, was sie rein mathematisch auch sind.
Ich weise aber nochmals auf die extreme Schwachstelle der Theorie hin:

Rein mathematisch werden nur OBERFLÄCHEN fassbar - bereits VOR dem Hinein-Fallen in das Schwarze Loch ! Halte man sich vor Augen, dass ein Hologramm nichts anderes ist als eine im Raum dargestellte 3-dimensionale OBERFLÄCHE ! Daran ändert sich auch nichts, wenn Susskind dieses Argument etwa zu entkräften versucht, dass es sich genau so verhalten würde, wenn man statt DIESES Oberflächen-Bildes eine Computer-Tomographie nehmen würde. Eines solchen Hinweis halte ich nicht nur für hochgradig zirkulär - nein: Zudem kann DIES mit den derzeitigen mathematischen Modellen schon nicht mehr nachvollzogen werden!
Das typische dieser Zirkularität im Denken ist jedoch (wie immer und immer wieder) eine GLEICH-SETZUNG! Oberflächen-Bilder werden mit realen, 3-dimensionalen Objekten, die sich noch dazu im Fluss der Zeit befinden, gleich-gesetzt. Die tief-gehende Fehl-Interpretation, die hier ihren Ausgangspunkt hat, berücksichtigt nicht, dass komplex strukturierte Gebilde die Charakteristik ihrer Eigenart ja eben gerade durch besondere räumliche Anordnungen erhalten, die sich durch die Zeit hindurch bewahren!
Selbstverständlich bekomme ich ein erweitertes (in die Tiefe gehendes) Bild eines Menschen, wenn ich diesen durch einen Computertomographen schicke. Ein REAL in hauchdünne Scheiben zerschnittener Mensch ist aber?

TOT !

Die alles um- und überspannende Fehl-Interpretation der modernen Physik liegt aber in einem Glauben begründet, die diese hier an einem konkreten Beispiel aufgezeigte Gleich-Setzung NOCHMALS ausweitet und zum Boden der Physik ganz allgemein macht (oder glaubt machen zu müssen / zu dürfen / zu sollen):

1. UNTERHALB der Strings finden wir NICHTS mehr
2. Strings haben bereits KEINE Dicke mehr - der Durchmesser der Fäden ist NULL
3. Auch Branes haben keine Dicke mehr und sind "rein" 2-dimensional
4. Der Aufbau höherer Dimensionen aus Gebilden, die IN-SICH keine räumliche Ausdehnung mehr
haben, muss demnach ILLUSION sein

Das ist der derzeitige Stand, auf den man sich in der "hoch-wissenschaftlichen Welt" zu einigen beginnt.
Ich halte dies alles für grundlegend falsch und gebe den Strings die Dimension einer DICKE. Damit sind sie (für mich) Gebilde, die bereits IN-SICH 3-dimensional sind. Für mich gibt es daher nur einen einzigen Sprung:

Das ist der Sprung vom NICHTS in die 3-Dimensionalität.

Und in der 3-Dimensionalität (einer dem Sein also grundlegend anhaftende Eigenschaft) lassen sich dann alle nur erdenklichen "Zusatz-Dimensionen" simulieren.
Für mich gilt es also gerade umgekehrt herum: Was ÜBER und was UNTER 3 Dimensionen liegt, DAS ist nicht real. Unterhalb von 3-D gibt es nur das NICHTS. Reine 1- oder 2-dimensionale Gebilde sind mathematische, aber nicht reale Konstrukte. Höhere als 3-dimensionale Gebilde sind ebenfalls nur mathematische Konstrukte, die PHYSIKALISCH real sind/werden und daher auch nur physikalisch/mathematisch wahrzunehmen sind: Es entsteht ein GAP - die physikalische Welt lässt sich nicht in die Wahrnehmungswelt (die 3-dimensional ist und bleibt) übertragen. Die Physik kann in dieser Wahrnehmungswelt nicht Gestalt annehmen, weil sie nur mathematische Simulation ist!
So - damit habe ich die Welt ziemlich auf den Kopf gestellt.
Und so wird es denke ich noch eine ganze Ecke weiter-gehen - denn bei tieferen Betrachtungen meines 4-dimensionalen-LED-Anzeigen-Modells sind wir ja noch lange, lange nicht angekommen.

Komme ich heute zum Schluss zu einer hoffentlich wirklich endgültigen Betrachtung des Holographischen Prinzips:

Für mich ist die Bekenstein-Grenze also unbedingt richtig. Das Holographische Prinzip ist nur eine falsche Interpretation. Wie ich mehrfach schon angeschnitten habe, beschäftigt sich dieses Prinzip überhaupt nicht im Geringsten mit DEM unabdingbaren Part des Informations-Begriffs, der komplexe Strukturen und ihre Wahrung über die Zeit kennzeichnet. Was übrig bleibt von Information ist ein letzter "Hauch" des zu fordernden Informations-Begriffs. Es geht um Informations-Bausteine - aber kein Stück um die Betrachtung ihrer räumlichen Anordnung und ihrer zeitlichen Persistenz.
Deshalb komme ich nun nochmals zu meiner Interpretation der Bekenstein-Grenze, die mit Holographie nicht das Geringste zu tun hat:

Kernaussagen sind:

1. Information kann NIE vollkommen verschwinden.
2. In einem Schwarzen Loch existiert die Rest-Information in maximal möglicher Entropie resp. minimal möglicher Negentropie. Das bedeutet NICHT totales Chaos! Vielmehr wird dadurch ausgedrückt, dass die gesamten, durchaus sauber "gelagerten" Informations-Bausteine NICHTS-SAGEND geworden sind. In einem Schwarzen Loch bewahren sich nur noch Informations-Bausteine in dichtest-möglicher Packung.
Aus Schrift ist wieder Tinte in einem Fass geworden !
Für das "Pack-Maß" existiert eine prima-vista seltsam erscheinende Relation. Diese Relation so auszudrücken: Wie viel Tinte in das Fass passt zeigt die Oberfläche des Tintenfasses - das wäre völliger Blödsinn.
Es besagt vielmehr, dass schon das Bild mit der Tinte FALSCH ist. Die Information, um die es im SEIN geht, ist nicht wie Tinte in einem Fass - eher wie Tinte in einer Patrone von HP (die schon früher von diesem Prinzip gewusst haben müssen):
Die Patrone ist NIEMALS ganz voll.
Wir übertragen das aber in ein anderes Bild: Es bleibt auch beim dichtesten Packmaß eine Mindest-Neg-Entropie (Ordnung) erhalten. Diese steht in einem Verhältnis zur Oberfläche des Lager-Raumes (Schwarzen Loches) und NICHT im Verhältnis zu seinem Volumen.
3. Vice versa von DIESER Oberfläche auf andere Volumina in Fortschreibung der im Schwarzen Loch gegebenen Relation halte ich bereits für NICHT statthaft.
4. EINES wird aber deutlich: Komplexer werdende und sich höher strukturierende Information ist RAUM-GREIFEND ! Komplexere Information braucht MEHR Raum als einfach nur gestapelte Informations-Bausteine. Ganz klar: Bei Hornbach findet Mike Krüger seine Baumaterialien dicht gestapelt vor. Sein Haus, das er daraus baut, braucht MEHR Raum. Und das Haus eines Blödmannes, der nix von Statik versteht und deshalb seine Mauern in 3-facher Dicke baut, ergibt bei gleicher Ausgangsmenge Baumaterials ein kleineres Haus als das von Mike Krüger, der sich von seinen Werbe-Einnahmen einen Architekten leisten kann.

Als groben Anhaltspunkt für die in Informationen steckende Komplexität und Strukturiertheit will ich mir mal das Phantasie-Maß KS aus den Rippen schütteln.

Es sei:

Y-Achse A Durchschnittlich Zahl verfügbarer Werkzeuge pro Lösung Ø Wzg
X-Achse B Durchschnittliche Zahl der Lösungen pro Zeit-Einheit Ø Lsg

A x B = KS (Einheit: Werkzeuge/sec) - dies kann als Fläche dargestellt werden.

Dann ist mit dieser Fläche ein MINDESTENS notwendiger Raumbedarf korreliert (mehr Raum geht immer - weniger aber nicht). Und das Volumen des notwendigen Raumes ergibt sich, wenn man aus der Fläche eine zusammenhängende, umhüllende Oberfläche bildet:
Der umhüllte Raum enthält das mindestens notwendige Volumen - für den Fall, dass sich das Holographische Prinzip als durchgängig gültig heraus-stellen sollte.

sunaJJanus schrieb:Der umhüllte Raum enthält das mindestens notwendige Volumen - für den Fall, dass sich das Holographische Prinzip als durchgängig gültig heraus-stellen sollte.

Die Entropie Grösse ist immer im Verhältnis zum Raum zu sehen.

Die Entropie-Größe ist immer im Verhältnis zum Raum zu sehen.


Antwort im wieder etwas voraus-laufenden PDF:

https://dl.dropboxusercontent.com/u/24509641/Das%20selbst-identische%20Universum.pdf

Muss sehen, ob ich noch etwas korrigieren muss. Nehme es dann wieder in den nächsten Post.

Wäre auch dankbar für Rückmeldungen darüber, ob das langsam ankommt, was ich sagen möchte von wegen Raum-Bedarf einer sich komplexer strukturierenden Information.

Fritzchens Einwurf zeigt, dass bis jetzt noch nichts angekommen zu sein scheint.

sunaJJanus schrieb:Fritzchens Einwurf zeigt, dass bis jetzt noch nichts angekommen zu sein scheint.

"Hawking erkannte 1974 nach Vorarbeiten des israelischen Physikers Jacob Bekenstein, dass Schwarze Löcher eine formale Entropie und somit auch eine formale absolute Temperatur T haben."

"Das holografische Prinzip postuliert, dass jede Information, die den Ereignishorizont eines Schwarzen Loches überschreitet, auf der vom Schwarzschildradius aufgespannten Grenzfläche vollständig codiert wird, ähnlich einem zweidimensionalen Hologramm, das eine dreidimensionale Bildinformation enthält."

Heisst der Thread Wie wendet man erfolgreich die Wärmelehre auf schwarze löcher an?




Davon ab das sowohl Hawking Strahlung sowie die Stringtheorie von der du ja scheinbar ausgehst, noch nicht bestätigt wurden, also viel Spekulatius und was das Universum und das selbst damit zu tun hat habe ich überhaupt nicht kapiert, noch welchen Wert von Erkenntnis das überhaupt mit sich bringen soll.

Was im PDF seit gestern also bereits enthalten ist, hier nachträglich wie angekündigt gepostet:


Zitat: "Die Entropie-Größe ist immer im Verhältnis zum Raum zu sehen"

Auf ein Neues - irgendwann wird es jedem klar geworden sein. Und ja, richtig - bei den Grundlagen sollte man einigermaßen sicher sein:

Also nochmals zum Beispiel

a) Baumaterialien bei Hornbach - b) Baumaterialien verbaut im Haus von Mike Krüger.

Gestochen ausgedrückt ist die Entropie ein Maß für die Anzahl der Mikrozustände, durch die der beobachtete Makrozustand eines Systems (hier Mike Krügers Haus) realisiert werden kann. Im Prinzip wäre dafür ein Bauplan notwendig, der für jeden einzelnen Stein die Position im Haus anzeigt, die er einzunehmen hat. Ein Teil der Anweisungen befindet sich in den Gehirnen der Bauarbeiter und es wäre zu berücksichtigen, dass viele Steine kommutativ / d.h. austauschbar sind, weil völlig gleich. Das Ganze muss schließlich noch als Prozess gesehen werden (Dimension Zeit kommt hinzu).
Jedenfalls verringert das "Verbauen" Entropie und vergrößert sie nicht.
In der Thermodynamik ist die Beschreibung der Entropie einigermaßen einfach und kann zumal bei Gasen oder bei Flüssigkeiten in der Einheit der Energie (Joule) pro Grad Kelvin berechnet bzw. ausgedrückt werden:

S =



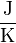
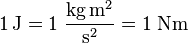
Bei konstanter Temperatur wächst die Entropie demnach mit Zunahme der Masse.
Masse korreliert IMMER mit einem Volumen.
Zunahme der Masse bedeutet (wieder bei konstanter Temperatur) gleichsinnig zunehmendes Volumen (2 10-Liter-Eimer Wasser = 2 mal 10 kg Masse).

Isoliert betrachtet und ohne dass wir uns darum scheren, wie es zustande-kommt und was es normalerweise bedeutet, findet sich also bei der Entropie schon immer eine Relation zu einer Quadrat-Länge - und die ist immer vorstellbar auch als Fläche. Auch wenn so ein "Hinein-Deuten" eines Längenquadrats in der Formel nicht im Sinne des Erfinders ist: Schließlich kommt das so zustande, dass man zunächst von einer Kraft N = kg·m·s−2 ausgegangen war und die Arbeit W verrichtet ist, wenn diese Kraft längst eines Weges auf eine Masse wirkte:

Wenn ich mein Spielzeug-Auto (1 kg schwer) über einen Meter hinweg mit 1 ·m·s−2 beschleunige, habe ich (bzw. die Maschine) die entsprechende Arbeit von 1 Nm (1 Newtonmeter) geleistet, was dimensional der selben Energie E (ebenfalls Nm) entspricht. All das beiseite-gewischt springt uns trotzdem in die Pupille, dass ich in der Entropie-Formel S oben eben ein Längenquadrat und damit ergo eine Fläche habe ! Meter mal Meter gibt nun eben einmal Quadratmeter...

Und nun gibt es eine wunderbare Anekdote über Jacob Bekenstein: Als dieser noch Student war, soll er im Hörsaal einmal aufgespritzt sein und ausgerufen haben:

"Black holes have Entropie !"

Bis zu diesem Zeitpunkt dominierte Steven Hawking die Forschung über Schwarze Löcher fast alleine - bis zu diesem Zeitpunkt war er der Überzeugung, Information würde in Schwarzen Löchern zum einen komplett verschwinden, zum anderen in einem kleinen Teil ausgestoßen werden (Hawking-Strahlung).

Über den Kern-Radius eines Schwarzen Loches konnte man nichts sagen - aber man dachte, dieser sei extremsten-falls Null (nicht mehr definierbar), womit der Begriff Singularität geboren war.

Allemal ist es so, dass man wohl die Masse eines Schwarzen Loches bestimmen kann - jedoch NICHT dessen (Kern-)VOLUMEN.

So - dies nun ist der Knackpunkt der ganzen Geschichte:

Wenn ich ein Warenlager habe, in dem NICHTS drinnen ist, dann stirbt damit auch der Begriff der Entropie. Er wird unsinnig. Wenn ich keine Waren im Lager habe, können diese dort weder geordnet noch ungeordnet herum-liegen.

Nach Hawkings ursprünglicher Auffassung hatten Schwarze Löcher also KEINE Entropie.
Als es Jacob Bekenstein vom Sattel riss und er den Funken seiner Erleuchtung spürte, entsann er sich wohl der Interpretationsmöglichkeit der Entropie:

Sie enthielt ein Längenquadrat/eine Fläche als Dimension. Und er fand seine Formel



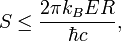
bei der sich nun über die Kugel-Oberfläche am Schwarzschild-Radius ein dazu-gehöriges Kugel-Volumen definiert für einen astronomischen Körper (das SL), dessen EIGENTLICHES Volumen man nicht kennt.

Gerard t'Hooft verallgemeinerte die Formel Bekensteins dann noch:



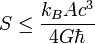
- und in t'Hoofts Formel tritt die Fläche A aus der Verborgenheit nun ans Licht:
A ist nichts anderes als die OBERFLÄCHE eines sphärischen Raumbereichs (also eines Raum-Volumens) das von eben dieser Oberfläche A begrenzt wird.

Hier steht die Entropie S also klar ersichtlich in einem Verhältnis zu einer Fläche A !
Und ich wiederhole nochmals, was ich im vorletzten Post oben dargelegt habe (versucht habe, darzulegen...) :

Minus erster Hauptsatz - minus first law of physics (der Thermodynamik):

Die Entropie in einem sphärischen Raumbereich (in einem Volumen) steht (nach DIESER Formel) klar ersichtlich in einem Proportionalitäts-Verhältnis zur Oberfläche A (der Oberfläche beim Schwarzschild-Radius / Event-Horizon). Verdoppelung der Oberfläche A bewirkt (nochmals: nach DIESER Formel !) eine Verdoppelung der Entropie.

Es ist die Entropie, die in einem Schwarzen Loch einer bestimmten Größe enthalten ist.

Die Größe des Schwarzen Loches wiederum kann NICHT unmittelbar über ein Volumen ausgedrückt werden: Ein SL ist eine Singularität !

Auf jeden Fall aber ist ein Volumen immer proportional zu einer Masse. Die Masse eines Schwarzen Loches kann ermittelt werden.

Und jetzt bitte gaaanz langsam lesen:
Wenn der Schwarzschild-Radius proportional zur Masse wächst (doppelte Masse, doppelter Radius) und die Masse stets einem VOLUMEN adäquat ist, das VOLUMEN in diesem Fall aber nur über den Radius definiert werden kann/muss (das EIGENTLICHE Volumen einer Singularität ist NICHT definiert) so steht hier die Masse NICHT mehr in einer direkten Proportionalität zur Entropie.

Normalerweise geht also der Weg über Masse zum adäquaten Volumen und das Maß der Entropie ist in der "normalen Welt" proportional zum Volumen. In einem Schwarzen Loch muss jedoch von einer Informations-Stapelung bzw. von einer Informations-Dichte ausgegangen werden, die JENSEITS der "normalen Welt" angesiedelt ist:
In der normalen Welt wird AUF-EINANDER gestapelt. In einem Schwarzen Loch wird INEINANDER gestapelt.
Es ergibt sich somit KEIN Proportionalitäts-Verhältnis mehr zwischen Masse und Kern-Volumen, weil dieses Kern-Volumen eines Schwarzen Loches eben nicht mehr definiert / nicht mehr zu ermitteln ist! Über die Masse eines SL kann also NICHT MEHR auf das Kern-Volumen einer Singularität geschlossen werden !
Vielmehr (nochmals auf die Formel von t'Hooft schauen) wird hier ZUERST eine Oberfläche definiert über dem Schwarzschild-Radius.

Die Entropie und damit die Informationsmenge in einem Schwarzen Loch ist NICHT MEHR einem Volumen direkt proportional, sondern DIESER OBERFLÄCHE !

Herumgedreht bedeutet dies (was aber eigentlich unsinnig, weil tautologisch ist), dass (wenn die Masse dem Radius proportional ist und die Entropie/Information der Fläche, die sich über das Quadrieren des Radius ergibt) die Entropie/Information nun ihrerseits wiederum proportional zum Quadrat der in einem Schwarzen Loch enthaltenen Masse ist.

Das hört sich also völlig kontra-intuitiv an - aber das besagt eben nichts anderes, als dass DIESES Volumen (welches NICHT das un-bestimmbare Kern-Volumen des SL ist) in einer Korrelation zu einer Fläche steht! Es geht in dieser Beziehung um eine stets ZUERST ermittelte FLÄCHE (Oberfläche). Das dieser Oberfläche zugehörige Volumen wird SEKUNDÄR berechnet.

Das scheinbar Paradoxe bei dieser Angelegenheit wird sich auflösen, sobald man einen Begriff bekommen hat von
a) komplexer Information
und
b) der "Ineinander-Stapelung" (hyper-dichten Anordnung) in Schwarzen Löchern

Die Konsequenzen des neuen Gesetzes übertragen nochmals auf ein Lager: Das Lager ist niemals vollkommen leer. Information verschwindet nicht vollkommen. In dem Lager können sich maximal eine bestimmte Zahl von Informations-Bausteinen befinden in einem Zustand DORT maximaler Entropie / minimaler Negentropie.
Diese Werte stellen Grenzwerte dar und können NICHT über/unterschritten werden.


Und ein endliches Mal meine Interpretation:

Das Gesetz hat nach meinem Dafürhalten nichts mit einer 2-D-Speicherung der im SL selbst nicht mehr befindlichen Information AUF der umgrenzenden Fläche in Höhe des Event-Horizon zu tun.
Nach meiner Überzeugung schmilzt der Radius eines SL NICHT auf Null. Er bleibt endlich. Ein SL hat IMMER ein Kern-Volumen, wenn dieses auch nicht bestimmbar ist. Und IN diesem Volumen im Kern eines SL liegt die ins SL gefallene Information in einer maximalen Dichte / maximalen Unordnung / maximalen Entropie / minimalen Neg-Entropie hyperdicht gestapelt vor.

Bei einer Ineinander-Stapelung, von der wir bis jetzt keinen Begriff haben, kommt es (das müsste nun für jeden ersichtlich geworden sein) aber zu einer Ent-Koppelung von Masse an ein adäquates Volumen !

Wir haben bis heute jedoch keinen effizienten Begriff der Neg-Entropie, der Struktur-Bildung, der Bildung komplexer Strukturen, komplexer dynamischer Prozesse, die da wären:
Galaxien, Sterne, Planeten, Lebensformen

DAMIT sich Strukturen bilden können, DAMIT höhere und komplexere Strukturen entstehen können, BRAUCHT Information RAUM zur Entfaltung - MUSS lokal Entropie abnehmen / Negentropie zunehmen. Raum zur Entfaltung und Abnahme von Entropie ist aber eigentlich wieder eine Tautologie - es besagt zwei mal das gleiche.

Tatsache ist jedenfalls: Es BILDEN sich im Universum komplexere Strukturen!

Es bilden sich em-Wellen, Elementar-Teilchen, Atome, Moleküle, Gaswolken, Sterne, Galaxien, Planeten, Lebensformen.

DAMIT dies geschehen kann, BRAUCHT Information Raum / Leere / Platz.

Und der benötigte Raum, der benötigte Platz muss auch in einem Verhältnis stehen zur Komplexität der sich in diesem Raum bildenden Strukturen / Organisations-Strukturen, muss in einem Verhältnis stehen zu komplexen dynamischen Gebilden.

Dabei steigt der Raumbedarf NICHT im gleichen Verhältnis mit der über die Entropie fassbaren schlichten Mengen- bzw. Zahlenmäßigen Vergrößerung der Informations-Bausteine!

Organisiert sich Materie komplexer und immer komplexer, so brauchen DOPPELT so viele Informations-Bausteine nicht DOPPELT so viel Platz.

Das ist im Grunde genommen die Kern-Aussage.

Als Bild wieder das Lager: Mit einem Just-in-time-Management ist es möglich, dass erheblich mehr Information pro Zeit-Einheit durch ein Lager geschleust wird. Die Lager-Kapazität muss bei einem intelligenter werdenden Management für die Bewältigung der doppelten Menge NICHT das doppelte Lager-Volumen vorhalten.

So - und die Schlussbemerkung wieder mit einem Zeiger auf das Holographische Prinzip:

Sollte sich das Holographische Prinzip als durchgängig gültig erweisen und sollten wir irgendwann einen effizienten Begriff für komplexe Information entwickeln, so könnte es sein, dass der ZUSÄTZLICHE Raumbedarf bei komplexer werdenden Informations-Strukturen in EBEN diesem über das Holographische Prinzip beschriebenen und bis jetzt verwirrend erscheinenden Relation steht.
DAMIT sich Information höher strukturieren kann, braucht sie Raum. Nur in einem Tinten-Fass befindet sich Information in maximaler Entropie. Je komplexer die Informations-Strukturen, je mehr Raum fordert Information. Aber DIESE Art der Neg-Entropie-Zunahme wächst eben NICHT im gleichen Sinn wie das Volumen.

Koppelung der Negentropie rein an das Volumen hieße schlicht und ergreifend nur, dass man ein Tinten-Fass vergrößern aber niemals damit anfangen würde, zu SCHREIBEN!

Doppelt so HOCH strukturierte Information braucht nicht doppelt so viel Volumen.

Nochmals und ein endliches Mal zum Bild des Lagers:
Bei doppelt so intelligent organisierten Waren-Strömen braucht man für die Bewältigung der doppelten Waren-Menge pro Zeit-Einheit NICHT ein doppelt so großes Lager!

Vielleicht ist aber alles nur eine komplette Fehl-Interpretation und wir werden lediglich auf das Prinzip der hyper-dichten Stapelung verwiesen. Dann besagt das Ganze nichts anderes als dass im einem Kern-Volumen eines Schwarzen Loches (das wir rechnerisch nicht ermitteln können) eine Informations-Menge gelagert werden kann, die dem Quadrat der Masse des Schwarzen Loches entspricht. Das wäre der Rücksturz auf ein recht bescheidenes Resümee. Wie in der Quantenphysik würden wir also hier lediglich auf letzte Grenzen der Physik verwiesen werden, die in diesem Falle hießen:

Wir können zwar die Masse und die in einem Schwarzen Loch gespeicherte Information noch benennen, aber nicht mehr sein Kern-Volumen.

Wie sehr wir in dieser Hinsicht ins Eiern geraten können, das zeigt der Umstand, dass der Physiker rein mathematisch sehr oft das macht, was er eben machen kann:

Er geht beim Ansetzen des spekulativen Radius einer Singularität bis hinunter zur Null.

Im Verhalten des Physikers liegt aber eher der tiefere Grund für gestiftete Verwirrung - und nicht in der Natur. Wenn man einsähe, dass man eben über ein "Etwas", das man nicht kennt (und in diesem Falle auch niemals kennen-lernen WIRD) eben KEINE Aussage machen darf, dann wäre solchen Verwirrungen ein wenig vorgebeugt.

Ich setze spekulativ also ein Konzept dagegen, das mir erheblich sinnvoller erscheint:

Ich gebe den letzten Dingen der Welt ihre Dimension zurück und beraube sie nicht einer Dimension. Ob wir uns dieser Dimension (der DICKE eines String-Fadens) mathematisch werden je annähern können, muss die Zukunft zeigen. Aus ihr ergäbe sich dann aber konsekutiv alles weitere in einer wieder vollkommen intuitiv erfassbaren Art und Weise:

Wir dürften vielleicht davon ausgehen, dass bei hyper-dichter Stapelung String-Fäden bzw. die kleinsten Bausteine der Information (die SUs / Smallest Units) absolut dicht gepackt vorliegen wie die Tinte eben in einem Fass.
Fürs Schreiben auf Papier (2-dimensional) braucht es dann mehr Raum.
Fürs Schreiben in 3 Dimensionen braucht es noch mehr Raum.
Fürs Schreiben 4-dimensionaler Raum-Zeit-Prozesse braucht es wieder mehr Raum
- und schließlich für Komplexität braucht es wiederum Raum (wenn dieser sich nicht bereits aus dem zuvor Gesagten ergibt).
Letzterer nun stünde aber nicht mehr in einer Proportion zur schieren und rein zahlenmäßigen Zunahme der Informations-Bausteine.

Woran es krankt ist eben nur, dass wir bis heute wie gesagt keinen in der Physik anwendbaren Begriff haben für einen Komplexitäts-Zuwachs. Thats it.

Die Formeln müssten für den Allmy-Hintergrund leider invertiert werden. Das ist mir zu viel der Mühe. Sie befinden sich ja gut leserlich sowohl im PDF als auch in entsprechenden Wiki-Artikeln.

sunaJJanus schrieb:Ich gebe den letzten Dingen der Welt ihre Dimension zurück und beraube sie nicht einer Dimension.

Bei wie viel Dimensionen sind wir denn jetzt, gemäß der Stringtheorie?

@sunaJJanus
Ich fände es schade würde es hier nicht weitergehen.
Erlaube mir bitte dennoch die Kritik, das deine Ansichten etwas übersichtlicher formuliert sein könnten.

In so fern, als was hat sich den nun die Information deiner Meinung herausgestellt. Ich lass unter anderem von Dir... "als physisch", ist das so korrekt verstanden?

Z. schrieb:Erlaube mir bitte dennoch die Kritik, das deine Ansichten etwas übersichtlicher formuliert sein könnten

Und die Beiträge dürften gern etwas kürzer gehalten sein, mir fehlt da son bisschen die Möglichkeit, ein punkt um einzusteigen...

ich finde den thread auch sehr interessant.

doch der threadersteller sollte sich doch bitte etwas verständlicher ausdrücken...was sicherlich zum besseren verstehen deiner theorie,deiner gedankengänge etc beitragen könnte.
man liest einen absatz und beim nächsten absatz weiß man nicht mehr wirklich worum es eigentlich im ersten ging.
ich würde es schön finden wenn die ausschweifungen sich etwas eingrenzen und das kernthema verständlich dargelegt wird.

gruß.

Ja manch Verstand ist schwer zu folgen @sunaJJanus.

Ich bin ja begeistert und fühl mich irgendwie auch geehrt, dass ich erwähnt wurde und bildlich zusteuern konnte bei diesem komplexen Thema! Aber auch ich muss Dir sagen, das Du verhältniss mäßig viel Text schreibst. Was im Grunde ja nicht verkehrt ist, Aber ich Persönlich konnte auch irgendwann nicht mehr wirklich folgen. Und dann verliert man das Interesse. Wobei ich zugeben muss, da dieses Thema auch wohl hoch angesetzt ist, ich schon bei der Überschrift meine Probleme hatte :D

@sunaJJanus
Du hast wohl eine Intervention ausgelöst :D. Ich kann mich meinen Vorgängern nur anschließen. Wenn Du nicht das Interesse der Menschen verlieren willst, musst Du lernen Dich kürzer auszudrücken und deine Texte vielleicht noch visueller darstellen.

Es gibt für einen Menschen kaum schlimmeres, als nicht beachtet zu werden!

DTO schrieb:Es gibt für einen Menschen kaum schlimmeres, als nicht beachtet zu werden!

Vorallem dann wenn er sich so viel mühe gegeben hat wie @sunaJJanus ;)