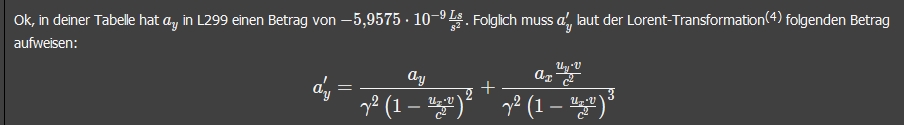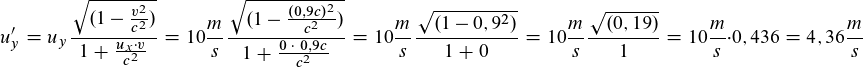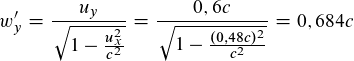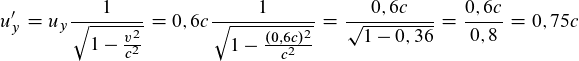mojorisin schrieb:Ich argumentier das es keine Koordinatentransformation braucht bei Werten aus demselben Inertialsystem.
Ok, in deiner Tabelle hat
a_y in L299 einen Betrag von
{-5{,}9575 \cdot 10^{-9}} \frac {Ls} {s^2}. Folglich muss
a_y' laut der Lorent-Transformation
(4) folgenden Betrag aufweisen:
a_y'= \frac {a_y} {\gamma ^2 \left ( 1- \frac {u_x \cdot v} {c^2} \right ) ^2} + \frac {a_x \frac {u_y \cdot v} {c^2}} {\gamma ^2 \left ( 1- \frac {u_x \cdot v} {c^2} \right ) ^3}
a_y'= \frac {-5{,}9575 \cdot 10^{-9} \frac {Ls} {s^2}} {1{,}4018^2 \left ( 1- \frac {0{,}7c \cdot 0{,}7c} {1c^2} \right ) ^2} + \frac {1{,}217 \cdot 10^{-8} \frac {Ls} {s^2} \cdot \frac {0{,}357c \cdot 0{,}7c} {1c^2}} {1{,}4018 ^2 \left ( 1- \frac {0{,}7c \cdot 0{,}7c} {1c^2} \right ) ^3}=5{,}9251 \cdot 10^{-11} \frac {Ls} {s^2}=0{,}018 \frac m {s^2}
Du aber behauptest
a_y' würde
0 \frac m {s^2} und
u_y' konstant
=0{,}5c betragen.
Wie gedenkst du den Widerspruch zu lösen?
So wie all die anderen, überhaupt nicht, einfach ignorieren?
Das deine Behauptungen in Bezug auf
a_y' und
u_y' falsch sind ist hiermit nachvollziehbar belegt. Es ist physikalisch unmöglich, das ein und dasselbe Objekt in einen Bezugsystem auf einer Achse eine Beschleunigung, und in einem anderen Bezugsystem auf der selben Achse keine Beschleunigung aufweist.
Das solltest du nun langsam mal zu Kenntnis nehmen, oder möchtest du behaupten die Lorentz-Transformation
(2)(4) hat für dich keine Gültigkeit, und das Beschleunigungen in der SRT nicht absolut sind
(5)?
Auch solltest du mal zur Kenntnis nehmen das newtonsche Mechanik
mojorisin schrieb am 20.01.2018:a_y'= \frac {\Delta u_y'} {\Delta t'}= \frac {0} {\Delta t'}=0
bei relativistischen Geschwindigkeiten nicht angewendet werden kann, deine obige Gleichung hier somit nichts zu suchen hat.
mojorisin schrieb:Und wenn sich ein Geschwindigkeit ändert und du aber dann deren Beschleunigung einfach = 0 setzt, dann ist das schlicht falsch.
Nein, du verstehst nur die Zusammenhänge nicht. Der Umkehrschluss müsste ja ebenso Gültigkeit besitzen. Du wirst jeden Tag mit
\approx 9{,}81 \frac m {s^2} beschleunigt - und - welche Geschwindigkeit hast du zwischenzeitlich?
Geschwindigkeit ist der Quotient aus Strecke durch Zeit, im GE also
\frac y t respektive
\frac {y'} {t'}. Das bedeutet für das GE, da sich die Detektoren auf der
y-Achse befinden und die Strecke zwischen den Detektoren
0{,}5Ls beträgt und auf der
y-Achse keine Längenkontraktion stattfindet, das
y=y' gilt. Die Strecke bleibt folglich für beide Systeme unverändert und beträgt unabhängig von der Relativgeschwindigkeit immer
0{,}5Ls.
Bei der Zeit verhält es sich anders, für das System
S' ist die Zeit
\left ( t' \right ) aus Sicht von System
S nicht konstant, sondern verändert sich in Bezug auf die Relativgeschwindigkeit zwischen den Systemen. Hier gilt
t'= \frac t \gamma.
Während System
S in seinem Bezugsystem auf der
y-Achse keine Änderung der Geschwindigkeit beobachtet, beobachtet System
S' auf der
y'-Achse, eben weil Geschwindigkeiten relativ sind, eine Geschwindigkeitsänderung
ohne das eine Beschleunigung auf der
y'-Achse stattfindet. Das ist kein Widerspruch, da eine Beschleunigung auf der
x'-Achse stattfindet. Da System
S' sich aber als ruhend defniert, führt diese Beschleunigung aus seiner Sicht nicht zu einer Geschwindigkeitsänderung auf der
x'-Achse.
Es hängt folglich vom Bezugssystem ab, ob auf einer Achse eine Beschleunigung ohne Geschwindigkeitsänderung und auf einer anderen Achse eine Geschwindigkeitsänderung ohne Beschleunigung beobachtet wird, während in einem anderen Bezugsystem auf einer Achse eine Beschleunigung mit Geschwindigkeitsänderung und auf einer anderen Achse weder eine Beschleunigung noch eine Geschwindigkeitsänderung beobachtet wird:
Prämissen bei t_0=0s: u_x=0c, u_y=0,500c, a_x=0,700 \frac {Ls} {s^2}, v=u_x:
Werte System
S bei
t=1{,}960s:
u_x= \frac {{a_x \cdot \left ( t-t_0 \right )}} {\sqrt {1+ \frac {{a_x}^2 \cdot \left ( t-t_0 \right )^2} {c^2}}} \cdot \frac {1} {\gamma _y}= \frac {{0{,}700 \frac {Ls} {s^2} \cdot \left ( 1{,}960s-0s \right )}} {\sqrt {1+ \frac {{0{,}700 \frac {Ls} {s^2}}^2 \cdot \left ( 1{,}960s-0s \right )^2} {1c^2}}} \cdot 0{,}866=0{,}700c \space \space \space \space \space \space \left (1 \right )
Somit haben wir alle Werte des ungestrichenen Systems
S:
v=0{,}700c
t=1{,}960s
u_x=0{,}700c
u_y=0{,}500c
a_x=0{,}700 \frac {Ls} {s^2}
a_y=0 \frac {Ls} {s^2}
Gesucht sind jetzt die Werte für das gestrichene System
S'. Die erhält man
nur über die Lorentz-Transformation:
t'= \frac {t} {\gamma _v}= \frac {1{,}960s} {1{,}400}=1,4s
\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space u_x'= \frac {u_x-v} {1- \frac {v} {c^2} \cdot u_x}= \frac {0{,}700c-0{,}700c} {1- \frac {0{,}700c} {1c^2} \cdot 0{,}700c}=0c \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \left (2 \right )
\space \space \space \space \space \space \space \space \space \space \space \space u_y'=\frac {\sqrt {1- \left ( \frac {v^2} {c^2} \right )}u_y} {1- \frac {v} {c^2}u_x}=\frac {\sqrt {1- \left ( \frac {0{,}700c^2} {1c^2} \right )} \cdot 0{,}500c} {1- \frac {0{,}700c} {1c^2} \cdot 0{,}700c}=0{,}700c \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \left (3 \right )
\space \space \space \space \space \space \space \space \space a_x'= \frac {a_x} {\gamma_v ^3 \cdot \left ( 1- \frac {u_x \cdot v} {c^2} \right ) ^3}= \frac {0{,}700 \frac {Ls} {s^2}} {1{,}4 ^3 \cdot \left ( 1- \frac {0{,}700c \cdot 0{,}700c} {1c^2} \right ) ^3}=1{,}923 \frac {Ls} {s^2} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \left (4 \right )
\space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space a_y'=a_y=0 \frac {Ls} {s^2} \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \left (5 \right )
mojorisin schrieb:a'y hat in meiner Tabelle den Wert 0 denn u'y ist konstant = 0,5c. DIese Werte sind aus Sicht von Bob, und das mach auch Sinn den während er vor sich hinbeschleunigt ändert sich für ihn an seiner Kugeluhr nichts.
Mich interessiert weniger dein Wunschdenken oder was du für sinnig hältst, sondern vielmehr das was du belegen oder nachvollziehbar erklären kannst ohne neue Widersprüche zu produzieren. Also Belege deine Behauptung bitte.
mojorisin schrieb:Das kommt daher das ich die WErte in Bob's System vorgegeben habe und dann in Alice's System transfromiert habe.
In dem hier diskutierten GE wurden aber nur Werte des ungestrichenen Systems angeben, folglich können die Werte für das gestrichene System nur über eine Transformation von
S nach
S' ermittelt werden. Nicht aber durch beliebiges bestimmen deinerseits, tiefen Blick in einer Glaskugel, oder gutem zusprechen irgendwelcher Götter.
mojorisin schrieb:DU gibst die Werte in ALices System vor und transformierst dann nach Bob. Dabei brauchst du natürlich auch keine numerische Integration denn du gehst von einem nichtbeschleunigten Bezugssystem aus.
Werfe doch mal mehr als nur einen flüchtigen Blick in meine
Excel-Tabelle, dann wirst du feststellen das es sich bei dem System
S' nicht nur um ein Beschleunigtes System handelt, sondern das du die Beschleunigung sogar frei wählen kannst. Unabhängig davon spielt die Beschleunigung keine Rolle, wenn nach Werten des gestrichenen Systems, bei
u_x=0{,}7c des ungestrichenen Systems, gefragt wird.
mojorisin schrieb:Es ist aber eh alles egal der Hauptpunkt ist folgender: Wenn Bob auf der Horizontalen beschleunigt, ergibt sich für die Vertikalgeschwindigkeit der Kugel eine Änderung für zumindest einen der beiden Beobachter.
Des Pudels Kern.
Bei mir ist es das System
S'. Dort ändert sich die Geschwindigkeit der Kugel auf der
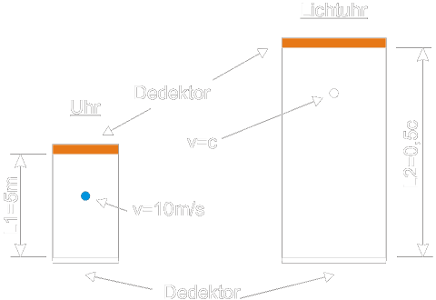
y'-Achse. Die Lichtuhr im System
S' geht aufgrund der Relativgeschwindigkeit
v=u_x=0{,}7c dilatiert, während die Kugel die Strecke von
y=y'=0{,}5Ls (Detektor zu Detektor) absolviert, zeigt die Lichtuhr in System
S exakt 1 Sekunde, und die Lichtuhr in System
S' exakt 0,714 Sekunden an:
u_y= \frac {y} {t}= \frac {0{,}5Ls} {1s}=0{,}5c
u_y'= \frac {y'} {t'}= \frac {0{,}5Ls} {0{,}714s}=0{,}7c
Bei dir verändert sich die Geschwindigkeit der Kugel im System
S auf der
y-Achse
ohne das eine Beschleunigung auf der
y-Achse vorliegt. Also eine Bewegungsänderung
ohne wirkende Kraft (kenne ich sonst nur von Pippi Langstumpf oder Esoterikern). Die Lichtuhr im System
S' dilatiert auch bei dir und zeigt 1 Sekunden an wenn die Kugel die Strecke von Detektor zu Detektor durchlaufen hat, während die Lichtuhr im System
S 1,4 Sekunde anzeigt:
u_y= \frac {y} {t}= \frac {0{,}5Ls} {1{,4}s}=0{,}357c
u_y'= \frac {y'} {t'}= \frac {0{,}5Ls} {1s}=0{,}5c
Der entscheidende Unterschied in meiner Darstellung besteht darin, dass ich keine "wirkende Kraft" aus den Hut zaubern muss um die Geschwindigkeitsänderung auf der
y'-Achse erklären zu müssen.
Du allerdings
musst erklären können woher die wirkende Kraft auf der
y-Achse kommt um die Geschwindigkeitsänderung im System
S auf der
y-Achse widerspruchsfrei zu begründen. Was dir bisher nicht gelungen ist, aber zwingend erforderlich ist.
mojorisin schrieb:Auch deine Kugeluhr unterliegt der Zeitdilatation, und geht daher aus Sicht von Alice zunehmend langsamer wenn Bob sie mitführt bei seiner beschleunigten Bewegung.
Ob die Kugeluhr dilatiert oder nicht, ist hier die Diskussionsgrundlage. Glaubst du diese mit einer bloßen Behauptung für geklärt halten zu können?
Wenn es dir mehr um "Glauben" als "Wissen" geht, kann man das tolerieren. Allerdings hat "Glauben" in dieser Rubrik keinerlei Aussagekraft.
(1) "Einführung in die Relativitätstheorie", 2. Auflage, Ray d'Inverno, Kapitel 3.7, Seite 55, von Wiley-VCH. ISBN: 978-3-527-40912-9
(2)
Wikipedia: Velocity-addition formula#Standard configuration(3)
Wikipedia: Velocity-addition formula#Standard configuration(4)
Wikipedia: Acceleration (special relativity)#Three-acceleration(5) "Einführung in die Relativitätstheorie", 2. Auflage, Ray d'Inverno, Kapitel 3.7, Seite 54, von Wiley-VCH. ISBN: 978-3-527-40912-9
