Schwierigkeit der Längenkontraktion

mojorisin schrieb:Danke für den Link. DIe Erklärungen basieren auf Minkowski-Diagrammen, die wir hier auch schon durchdiskutiert haben.

Richtig, ist hier auch schon durchgekaut worden. Ich finds nur nochmal sehr gut erklärt hier und es recht offensichtlich das die Dilatation eben nicht von der Uhr abhängt, sondern der Konstanz der LG geschuldet ist, denn das Licht übermittelt ja das Signal. Vielleicht äußert sich @pluss ja nochmal dazu.

mojorisin schrieb:Ok wir können das Beipiel etwas einfacher machen und kicken das System S' raus.

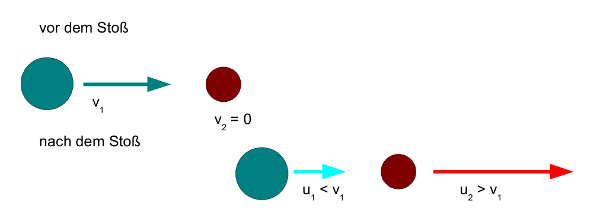
Also nurn noch das unbeschleunigte S. Wir haben die Kugel 2 die bewegt sichmit uy = 0,5c. Von links kommt Kugel 1 mit 0,7c. Nun stoßen sich beide so das Kugel 1 den gesamt IMpuls an Kugel 2 abgibt, aölso stehen bleibt und der gesamte IMpuls in Kugel 2 steckt.

Klar sollte sein der Gesamtimpuls vor dem Stoß sollte gleich sein wie der IMpuls nach dem Stoß .

Wie groß sind ux und uy nbach dem Stoß? @pluss behauptet ux =0,7c und uy =0,5c. das gilt es zu beweisen oder widerlegen.

Hierzu das Bild:



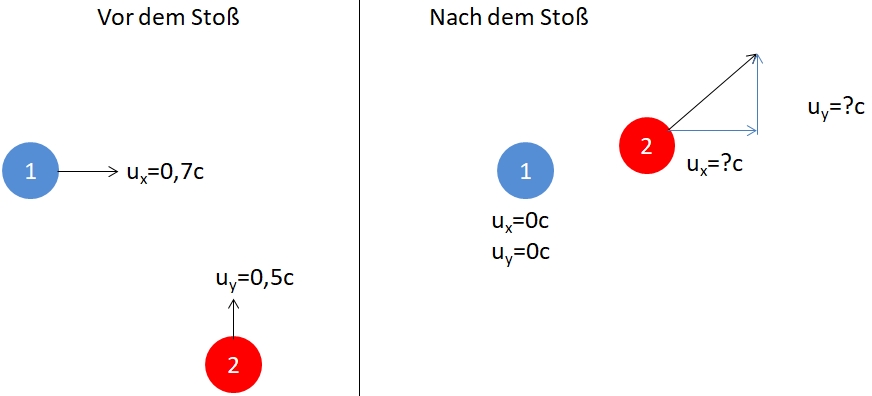
Somit können wir sämtliche Koordiantentransformationen und unterschiedliche System vernachlässigen, dsa einzige worauf wir uns einigen müssen ist das der IMpulserhaltungssatz gilt. Und das setze ich vorraus.

Ich erlaube mir die Aufgabe etwas umzuformulieren, um eine Situation zu erzielen die dem ursprünglichen GE entspricht. Dazu ändere ich

mojorisin schrieb:Von links kommt Kugel 1 mit 0,7c.

in

Von links kommt Kugel 1 mit unbekannter Geschwindigkeit.

ab, um zu erreichen das die Kugel 2 nach dem Stoß auf der x-Achse eine Geschwindigkeit von 0{,}7s aufweist.
Das bedeutet, Impuls und Geschwindigkeit der Kugel 1 muss zuvor berechnet werden. Handhaben wir es nicht so, erzielt die Kugel 2 auf der x -Achse nur eine Geschwindigkeit von 0{,}606c , und ein direkter Vergleich mit dem GE wäre so erschwert.


Da der Geschwindigkeitsvektor u_x der Kugel 2 nach dem Stoß 0{,}7c betragen soll, kann hier die Vektoraddition^[1] angewendet werden.

Vektoraddition


Syntax der Gleichung\begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} \begin{array}{c} \\ + \end{array} \begin{pmatrix} u_x \\ u_y \\ u_z \end{pmatrix}= \begin{pmatrix} w_x \\ w_y \\ w_z \end{pmatrix}= \begin{pmatrix} 0 \\ 0{,}5 \\ 0 \end{pmatrix} \begin{array}{c} \\ + \end{array} \begin{pmatrix} 0{,}7 \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} 0{,}7 \\ 0{,}5 \\ 0 \end{pmatrix}

\mathbf u=\sqrt {w_x^2+w_y^2+w_z^2}=\sqrt {0{,}7^2+0{,}5^2+0^2}=0{,}86c

Damit wäre die Kernfrage schon beantwortet.
Wir können das Ergebnis aber auch auf mehrfacherweise einer Überprüfung unterziehen. Unteranderem stellt sich ja auch die Frage welchen Geschwindigkeitsvektor \mathbf u = \lbrace u_x, u_y, u_z \rbrace und Impuls Kugel 1 haben muss, damit Kugel 2 nach dem Stoß u_x=0{,}7c aufweist.

Geschwindigkeitvektor Kugel 1 vor dem Stoß:

Syntax der Gleichung
\mathbf u_{1_{vor}} =\sqrt {\frac {\mathbf u_{2_{nach}}^2-v_y^2} {1- \frac {v_y^2} {c^2} } }=\sqrt {\frac {0{,}86c^2-0{,}5c^2} {1- \frac {0{,}5c^2} {1c^2} } }=0{,}808c

Impuls Kugel 1 vor dem Stoß:

Syntax der Gleichungp_1=m_0 \cdot \gamma_{u_x} \cdot u_x = 1kg \cdot 1{,}7 \cdot 0{,}808c=1{,}373 kg \cdot c \approx 411{.}600{.}000 \frac {kgm} {s}

Jetzt wissen wir schon welchen Geschwindigkeitsvektor \mathbf {u_1}= \lbrace u_x=0{,}808c, u_y=0, u_z=0 \rbrace =0{,}808c und Impuls p_1 die Kugel 1 vor dem Stoß haben muss, damit Kugel 2 nach dem Stoß einen Geschwindigkeitsvektor von u_x=0{,}7c aufweist.

Zur Kontrolle, ob Kugel 2 nach dem Stoß eine resultierende Geschwindigkeit von \mathbf u=0{,}86c aufweist, wenden wir das relativistische Additionstheorem für senkrechte zu ebene Geschwindigkeiten an:

Syntax der Gleichung\mathbf u_{2_{nach}}= \sqrt {\mathbf u_1^2+ \mathbf u_2^2 - \frac {\mathbf u_1^2 \cdot \mathbf u_2^2} {c^2}}= \sqrt {0{,}5c^2+ 0{,}808c^2 - \frac {0{,}5c^2 \cdot 0{,}808c^2} {1c^2}}=0{,}86c

Oder über die Vektoraddition für relativistische Geschwindigkeiten:



Syntax der Gleichung\begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} \begin{array}{c} r \\ + \end{array} \begin{pmatrix} {\frac {u_x} {\gamma_{v_y}}} \\ u_y \\ u_z \end{pmatrix}= \begin{pmatrix} w_x \\ w_y \\ w_z \end{pmatrix}= \begin{pmatrix} 0 \\ 0{,}5 \\ 0 \end{pmatrix} \begin{array}{c} r \\ + \end{array} \begin{pmatrix} {\frac {0{,}808} {1{,}155}} \\ 0 \\ 0 \end{pmatrix}= \begin{pmatrix} 0{,}7 \\ 0{,}5 \\ 0 \end{pmatrix}

\mathbf u=\sqrt {w_x^2+w_y^2+w_z^2}=\sqrt {0{,}7^2+0{,}5^2+0^2}=0{,}86c

Dabei möchte ich es aber nicht belassen, denn es gibt noch mehr Möglichkeiten zu belegen das obige Berechnungen widerspruchsfrei sind, und zwar mit der Impulserhaltung \left ( p_1+p_2 \right ):





Syntax der Gleichungp_1=m_0 \cdot \gamma_{u_x} \cdot u_x = 1kg \cdot 1{,}7 \cdot 0{,}808c=1{,}373 kg \cdot c \approx 411{.}600{.}000 \frac {kgm} {s}

p_2=m_0 \cdot \gamma_{v_y} \cdot v_y = 1kg \cdot 1{,}155 \cdot 0{,}5c=0{,}5773 kg \cdot c \approx 173{.}205{.}000 \frac {kgm} {s}

\mathbf u_{2_{nach}}= \frac {c} { \sqrt {1+ \frac {m_2^2 \cdot c^2} {p_1^2+p_2^2} } }= \frac {1c} { \sqrt {1+ \left ( \frac {1{,}155kg \cdot 1c} {0{,}5773kg \cdot c + 1{,}373 {kg \cdot c} }\right )^2 }}=0{,}86

Der Gesamtimpuls der Kugel 2 nach dem Stoß beträgt somit

Syntax der Gleichung\mathbf p_{2_{nach}}=m_0 \cdot \gamma_{\mathbf u_{2_{nach}}} \cdot \mathbf u_{2_{nach}} = 1kg \cdot 1{,}96 \cdot 0{,}86c=1{,}687 kg \cdot c \approx 506{.}116{.}700 \frac {kgm} {s}

Eine vektorielle Addition der Impulse muss zu einem gleichen Betrag führen:




Syntax der Gleichungp_1=m_0 \cdot \gamma_{u_x} \cdot u_x = 1kg \cdot 1{,}7 \cdot 0{,}808c=1{,}373 kg \cdot c \approx 411{.}600{.}000 \frac {kgm} {s}

p_{2_{nach}}=m_0 \cdot \gamma_{\mathbf u_2} \cdot v_x = 1kg \cdot 1{,}96 \cdot 0{,}5c=0{,}98 kg \cdot c \approx 294{.}000{.}000 \frac {kgm} {s}

\mathbf p= \sqrt {p_1^2+p_2^2}= \sqrt {\left (1{,}373 kg \cdot c \right )^2 + \left (0{,}98kg \cdot c \right )^2}=1{,}687 \approx 506{.}116{.}700 \frac {kgm} {s}

So, das ist meine Vorstellung einer schlüssigen und nachvollziehbaren Lösung.
Da das aber möglicherweise nicht ausreicht, möchte ich diese Aussage

mojorisin schrieb:Es gibt in dieser Hinsicht keinerlei Spielraum. Genau wie im klassichen Fall müssen die Energien und Impulse erhalten bleiben. Mathematisch gibt es genau eine Lösung die diese Bedingung erfüllt, daher sollte es keine Diskussion geben.

aufgreifen und belegen, wie ein solcher Widerspruch aufgezeigt werden kann. Dafür gibt es zwei (vielleicht auch mehr, ich kenne jedoch nur diese beiden) Gleichungen:

Erste Gleichung:

Zweite Gleichung:

Syntax der Gleichungu_x= \frac {1} { \sqrt {1+ \frac {m_0^2} {p_x^2} } } \cdot \beta_{y_{vor}}

\mathbf u= \frac {c} { \sqrt {1+ \frac {m_2^2 \cdot c^2} {p_1^2+p_2^2} } }

Diese Gleichungen wende ich nun mit Beträgen aus @mojorisin Excel-Tabelle an, um zu überprüfen ob ein Widerspruch auftaucht.



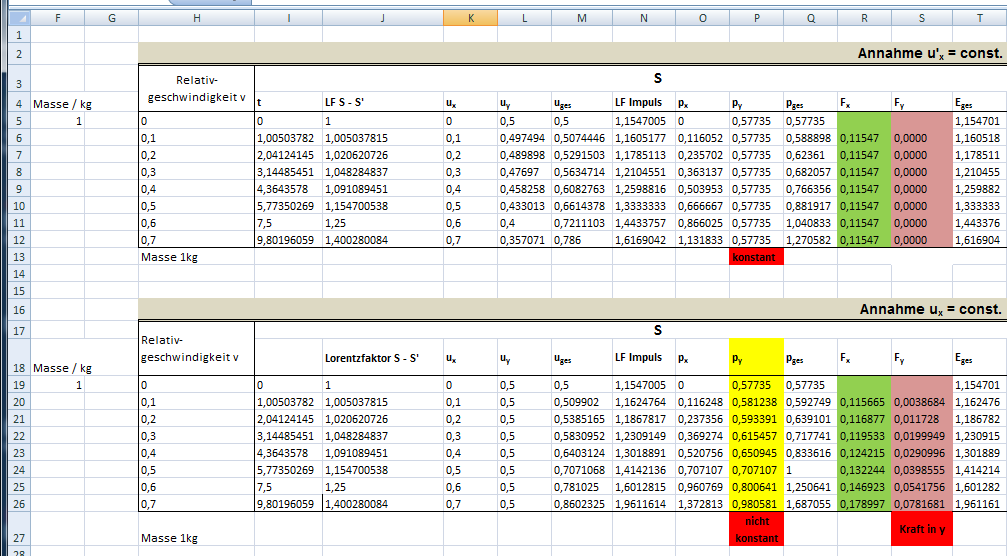
Obere Tabelle System S:

Syntax der Gleichungu_x= \frac {1} { \sqrt {1+ \frac {m_0^2} {p_x^2} } } \cdot \beta_{y_{vor}}= \frac {1} { \sqrt {1+ \left (\frac {1kg} {1{,}1318kg \cdot c }\right )^2}} \cdot 0{,}866=0{,}65c
Das ist ein Widerspruch, denn laut der Tabelle soll u_x=0{,}70c betragen.
Damit ist belegt, dass der Impulserhaltungssatz verletzt wurde.


Syntax der Gleichung\mathbf u= \frac {c} { \sqrt {1+ \frac {m_0^2 \cdot \gamma_{y_{vor}} \cdot c^2} {p_1^2+p_2^2} } }= \frac {1c} { \sqrt {1+ \left ( \frac {1kg \cdot 1{,}155 \cdot 1c} {0{,}5773kg \cdot c + 1{,}1318 {kg \cdot c} }\right )^2 }}=0{,}829c
Das ist ein Widerspruch, denn laut der Tabelle soll \mathbf u=0{,}786c betragen.
Damit ist belegt, dass der Impulserhaltungssatz verletzt wurde.

Untere Tabelle System S:

Syntax der Gleichungu_x= \frac {1} { \sqrt {1+ \frac {m_0^2} {p_x^2} } } \cdot \beta_{y_{vor}}= \frac {1} { \sqrt {1+ \left (\frac {1kg} {1{,}3728kg \cdot c }\right )^2}} \cdot 0{,}866=0{,}70c
Kein Widerspruch vorhanden, denn laut Tabelle soll u_x=0{,}70c betragen.


Syntax der Gleichung\mathbf u= \frac {c} { \sqrt {1+ \frac {m_0^2 \cdot \gamma_{y_{vor}} \cdot c^2} {p_1^2+p_2^2} } }= \frac {1c} { \sqrt {1+ \left ( \frac {1kg \cdot 1{,}155 \cdot 1c} {0{,}5773kg \cdot c + 1{,}3728 {kg \cdot c} }\right )^2 }}=0{,}86c
Kein Widerspruch vorhanden, denn laut Tabelle soll \mathbf u=0,86c betragen.

[1] https://www.mathebibel.de/vektoraddition

P.S.: @skagerak, wie sich die Aufgabe ohne Mathematik lösen lässt folgt noch.

@pluss

Ich werde eine ausführlich Lösung posten, aber das wird noch etwas dauern. Vorab:

pluss schrieb:Damit wäre die Kernfrage schon beantwortet.

Also du passt einfach die Aufgabenstellung der gwünschten Antort an und schon ist die Frage beantwortet.

pluss schrieb:Handhaben wir es nicht so, erzielt die Kugel 2 auf der x x x-Achse nur eine Geschwindigkeit von 0,606c 0{,}606c 0,606c, und ein direkter Vergleich mit dem GE wäre so erschwert.

Wieso erzielt die Kugel auf der x-Achse nur eine GEschwindigkeit von 0,606? Oder anders gefragt:

Die Kugeln sind gleich schwer, also in der Ruhemass. Laut deiner Rechnung wird aber die Geschwindigkeit der Kugel 2 in x-Richtung nach dem Stoß dilatiert, in y-Richtung aber nicht.

Ist die y-Richtung irgendwie besonders konsistent gegenüber Zeitdilatation die x-Richtung aber nicht?
Was passiert wenn ich das Gedankenexperiment um 90° drehe?

Mehr dazu später ich werde meine Rechnung präsentieren, unter anderem werde ich zeigen das @skagerak Recht hatte das die Annahme das Kugel 1 liegen bleibt nicht haltbar ist.

Man sieht das in dem man in das Ruhesystem einer der Kugeln geht und das System so dreht das man einen eindimensionalen Stoß erhält. Dann kann man folgende GLeichungen benutzen:

Wikipedia: Elastic collision#One-dimensional relativistic

In diesem System wird dann Kugel 1 liegenbleiben. Dieses System ist aber gegenüber dem System in der Abbildung bewegt daher wird Kugel 1 im System der Abbildung nicht liegenbleiben.

@mojorisin
@nocheinPoet
@pluss
Was haltet ihr davon mal von der Kugel wegzukommen, zunmal sie für das Phänomen der Zeitdilatation eben auch völlig unerheblich ist?

mojorisin schrieb:Also du passt einfach die Aufgabenstellung der gwünschten Antort an und schon ist die Frage beantwortet.

Was ändert sich denn durch diese Anpassung außer den Geschwindigkeitsvektoren auf der x -Achse?
Glaubst du etwa die Vektoraddition ist nicht mehr gültig wenn Kugel 1 \mathbf u= \lbrace u_x, u_y, u_z \rbrace = \lbrace 0{,}7c, 0, 0 \rbrace aufweist?

Wie auch immer.

Ich nehme die Anpassung hiermit zurück.

Kein Bock über solche Nichtigkeiten zu diskutieren.

Die Lösung deiner Aufgabe lautet somit:







(Vergleiche den Gesamtimpuls mal mit Q12 deiner Excel-Tabelle)

Im Übrigen, die aufgezeigten Widersprüche deiner Excel-Tabelle bleiben erhalten, denn die sind von der Anpassung deiner Beispielaufgabe ohnehin nicht betroffen.

mojorisin schrieb:Wieso erzielt die Kugel auf der x-Achse nur eine GEschwindigkeit von 0,606?

Aus dem gleichen Grund weshalb Körper mit Ruhemasse nie auf Lichtgeschwindigkeit beschleunigt werden können.
Der Impuls geht nicht komplett in die Erhöhung der Geschwindigkeit ein, sondern ein Teil in die Erhöhung der Masse. Solche Basics sollte man aber schon wissen wenn man mit harten Bandagen über die SRT diskutiert.

mojorisin schrieb:Was passiert wenn ich das Gedankenexperiment um 90° drehe?

Verfügt man über Grundkenntnisse der relativistischen Mechanik, stellt sich die Frage nicht. Ich hatte es dir hier im Thread schon einmal aufgezeigt und vorgerechnet. Das Resultat hat neP heute Morgen wiederholt aufgezeigt, zwar ohne Impulsberechnung, aber nicht so schlimm:

nocheinPoet schrieb:Die Kugel bewegt sich im Ruhesystem S' von Bob mit 0,5 c auf der y-Achse. (Auch den Satz, schaden kann das sicher nicht ...)

Nun will Bob wissen, welche Geschwindigkeit Alice in ihrem Ruhesystem S für die Kugel auf der y-Achse messen wird. Darum transformiert er die bei sich gemessene Geschwindigkeit in das Ruhesystem S von Alice. Die beträgt dort dann 0,357 c. Alice misst also eine geringere Geschwindigkeit in ihrem Ruhesystem S als Bob in seinem Ruhesystem S' auf der y-Achse für die Kugel.

Es entspricht dann also exakt dem, wenn die Kugeluhr erst nach der Beschleunigung auf der x-Achse gestartet wird.
Bin gespannt was nach deiner Ansicht passieren würde. Folgt man deiner Logik, müsste sich die Geschwindigkeit auf der x-Achse reduzieren.

mojorisin schrieb:Mehr dazu später ich werde meine Rechnung präsentieren, unter anderem werde ich zeigen das @skagerak Recht hatte das die Annahme das Kugel 1 liegen bleibt nicht haltbar ist.

Natürlich ist so eine Annahme in einem GE haltbar.

mojorisin schrieb:Man sieht das in dem man in das Ruhesystem einer der Kugeln geht und das System so dreht das man einen eindimensionalen Stoß erhält. Dann kann man folgende GLeichungen benutzen:

Dein Beispiel mit den Kugeln ist aber ein zweidimensionaler Stoß.

mojorisin schrieb:Ich werde eine ausführlich Lösung posten, aber das wird noch etwas dauern.

Ist mir nur recht, habe momentan ohnehin viel zu tun. Also mach dir keinen Stress, ich warte lieber eine Woche satt über mehrdeutige Formulierungen oder Flüchtigkeitsfehler zu grübeln, nur weil man sich nicht die nötige Zeit zur Ausarbeitung genommen hat.

@pluss

pluss schrieb:Der Impuls geht nicht komplett in die Erhöhung der Geschwindigkeit ein, sondern ein Teil in die Erhöhung der Masse. Solche Basics sollte man aber schon wissen wenn man mit harten Bandagen über die SRT diskutiert.

Aber wieso passiert das bei dir nur auf der x-Achse und nicht auf der y-Achse?



Zur Erinnerung in den Impuls geht der Lorentzfaktor mit dem Gesamtgeschwindigkeitsvektor ein:






Daraus folgt:




WIe du siehst hängen die gesuchten Werte der x und y Komponenten der Kugel 2 selbst voneinander ab und der Lorentzfaktor für u_{y_{nach }} hängt selsbt von dem gesuchten ab.

--> Da u_{x_{nach}} nicht bekannt ist, ist \gamma_{nach} nicht bekannt und somit ist auch unbekannt. Du hast allerdings einfach 0,7c eingesetzt.

DU rechnest auch manchmal mit \gamma _{u_x} und manchmal mit \gamma _{u_y}. Der Lorentzfaktor berechnet sich aber immer mit der Gesamtgeschwindigkeitskomponente. Ich weiß aber nicht ob du damit nur Kugel 1 und 2 vor dem Stoß gemeint hast. Kann auch sein.

pluss schrieb:Natürlich ist so eine Annahme in einem GE haltbar.

Das stimmt schon im klassichen Fall nicht generell:


http://www.physik.wissenstexte.de/stoss.htm

Der Speziallfall das die Kugel liegen bleibt ist nur wenn die Massen gleich sind. Im GE sind zwar die Ruhemassen der Kugeln gleich durch die höhere Geschwindigkeit der Kugel 2 ist aber deren Trägheit erhöht. Das entspricht klassische einer höheren Masse.

Schon klassisch reichen die reinen Impulsbetrachtungen zur Lösung der AUfgabenstellung gar nicht aus weil sie zuviele Unbekannte haben mit zuwenig Gleichungen. Deswegen nimmt man die Energiebetrachtung mit hinzu.

pluss schrieb:Dein Beispiel mit den Kugeln ist aber ein zweidimensionaler Stoß.

Das mag so erscheinen aus dem betrachteten System. Man kann aber das Koordinatensystem so transformieren das daraus ein 1-dimensionaler Stoß wird. Das geht weil wir die Kugeln als Punktobjekte betrachten. Nur ausgedehnte Objekte führen auch zu einem echten 2D Stoß.

Wikipedia: Elastic collision#Two-dimensional

@pluss

pluss schrieb:Das Resultat hat neP heute Morgen wiederholt aufgezeigt, zwar ohne Impulsberechnung, aber nicht so schlimm:

nocheinPoet schrieb:Die Kugel bewegt sich im Ruhesystem S' von Bob mit 0,5 c auf der y-Achse. (Auch den Satz, schaden kann das sicher nicht ...)

Nun will Bob wissen, welche Geschwindigkeit Alice in ihrem Ruhesystem S für die Kugel auf der y-Achse messen wird. Darum transformiert er die bei sich gemessene Geschwindigkeit in das Ruhesystem S von Alice. Die beträgt dort dann 0,357 c. Alice misst also eine geringere Geschwindigkeit in ihrem Ruhesystem S als Bob in seinem Ruhesystem S' auf der y-Achse für die Kugel.

Es entspricht dann also exakt dem, wenn die Kugeluhr erst nach der Beschleunigung auf der xx-Achse gestartet wird.

Du ich hatte Dir explizit schon erklärt, dass meine Beschreibung auch dann "exakt dem" entspricht, wenn die Kugeluhr schon vor der Beschleunigung gestartet wurde.

Es ist physikalisch egal, ob erst die Kugeluhr gestartet wird und dann beschleunigt und ob sie erst nach der Beschleunigung auf der x-Achse gestartet wird.

Eben auch wegen dem Relativitätsprinzip, welches Du ja explizit nicht anerkennen magst. :D

Die Ruhemasse der Kugel in der Uhr ändert sich nicht, sie ist vor und nach der Beschleunigung gleich. Nur diese Masse ist im System S' von Bob interessant, dort wird dann der Impuls auf die Kugel übertragen, auf der y-Achse.

Wie auch immer der Impulsgeber geartet ist, der wird vor und nach der Beschleunigung der Kugeluhr auf der x-Achse immer den gleichen Impuls auf die Kugel übertragen. Und auch die Ruhemasse hat sich im System S' von Bob nicht geändert.

Natürlich wird dann die Kugel im System S' von Bob immer dieselbe Geschwindigkeit auf der y-Achse besitzen.

mojorisin schrieb:Du hast allerdings einfach 0,7c eingesetzt.

Sag mal willst du mich verarschen?
Was hätte ich denn statt 0{,}7c für einen Betrag nehmen sollen, vielleicht 0{,}815 ?

mojorisin schrieb am 11.02.2018:Wir haben die Kugel 2 die bewegt sichmit uy = 0,5c. Von links kommt Kugel 1 mit 0,7c.

mojorisin schrieb:Schon klassisch reichen die reinen Impulsbetrachtungen zur Lösung der AUfgabenstellung gar nicht aus weil sie zuviele Unbekannte haben mit zuwenig Gleichungen. Deswegen nimmt man die Energiebetrachtung mit hinzu.

Also ich habe deine gestellte Aufgabe schon gelöst. Vielleicht solltest du dich zunächst einmal auf deine Lösung der Aufgabe konzentrieren, als meine zu kritisieren. Da du dein Ergebnis noch gar nicht kennst, solltest du nicht von vornherein ausschließen, dass es meinem entsprechen könnte.

@mojorisin

Ich bin noch immer wirklich dafür, den Impuls auf der y-Achse im System S' von Bob zu behandeln. Einmal vor und einmal nach der Beschleunigung des Systems S' gegenüber dem System S von Alice.

Und dann könnte man beides noch mal machen, nur dieses mal beschleunigt man dann das System S von Alice gegenüber dem System S' von Bob.

Es ist recht leicht zu zeigen, dass in allen vier Fällen der Impuls auf der y-Achse auf die Kugel im System S' von Bob gleich ist und auch die Ruhemasse in allen vier Fällen gleich bleibt.

Damit ist der Drops dann auch gelutscht.

Alle Uhren laufen eben dilatiert, wenn sie bewegt sind, es ist egal ob sie mechanisch sind, oder vor oder nach einer Beschleunigung gestartet werden und auch egal ist es, ob sie selber beschleunigt wurden, oder das andere System. Alleine die Geschwindigkeit ist entscheidend.

Hier muss dann eben @pluss mal erklären, wo und was genau sich in diesen vier Fällen denn unterscheiden soll. Wir haben in jedem Fall immer nur zwei Größen, den Impuls und die Ruhemasse. Daraus errechnet sich dann die Geschwindigkeit der Kugel.

Keine der beiden Größen ändert sich durch eine Beschleunigung im beschleunigten System. Der Impulsgeber wird im System S' von Bob immer denselben Impuls auf die Kugel übertragen, welche dort auch immer dieselbe Masse haben wird.

@pluss ist damit eindeutig widerlegt, und er sollte das auch schon länger begriffen haben. Ich halte das von ihm hier wirklich nur noch für Trollen.

@nocheinPoet
@pluss
@mojorisin
Also geht es konkret darum, ob die Uhr dilatiert wenn sie nach der Beschleunigung gestartet wurde?

Ich versuche mir das konkret vorzustellen.
Sie muss doch einfach auch dilatiert laufen. Wenn auch etwas anders als die andere Uhr, aber sie muss doch dilatiert laufen. Ansonsten könnte man die Dilatation doch auf diese einfache Weise umgehen, oder nicht?

nocheinPoet schrieb:Ich bin noch immer wirklich dafür, den Impuls auf der y-Achse im System S' von Bob zu behandeln. Einmal vor und einmal nach der Beschleunigung des Systems S' gegenüber dem System S von Alice.

Ja dann mach es doch mal. Die Sprache der Physik ist allerdings Mathematik, nicht Rhetorik.

skagerak schrieb:Also geht es konkret darum, ob die Uhr dilatiert wenn sie nach der Beschleunigung gestartet wurde?

Moin @skagerak, löse dich mal von dem Gedanken das wir hier über eine Uhr diskutieren. Die Kugel ist einfach nur ein Körper, dessen Bewegung wir ermitteln möchten. Eben vor und nach einer Beschleunigung auf der x-Achse.

@pluss
Ja aber ich dachte ursprünglich ging es darum und nun darauf hinaus. Steht die Ermittlung nicht dann dafür, dass eine Uhr dilatiert oder eben nicht dilatiert?

skagerak schrieb:Steht die Ermittlung nicht dann dafür, dass eine Uhr dilatiert oder eben nicht dilatiert?

Was für Eigenschaften muss ein Zeitmesser erfüllen, um als "Uhr" im physikalischen sinne zu gelten?
Was versteht man unter physikalischer Zeit?
Existiert die physikalische Zeit bereits, und wir brauchen sie nur noch messen?
Oder produzieren wir diese Zeit erst?
Ist Zeit das, was eine Uhr anzeigt?
Wann geht die Uhr richtig?
Dann wenn ich die Zeit mit einer andere Uhr vergleiche?
Woher aber weiß ich, dass die zweite Uhr richtig oder falsch geht?

@pluss
Puh! ... öhm, ich sag einfach mal: Ja
;-)

@pluss

pluss schrieb:Ja dann mach es doch mal. Die Sprache der Physik ist allerdings Mathematik, nicht Rhetorik.

Du die Sache ist doch nun echt klar, nur Du willst es nicht begreifen.

1. Willst Du bestreiten, dass im Ruhesystem S' von Bob alleine die Größe des Impulses und die Größe der Ruhemasse dort für die Geschwindigkeit der Kugel ausschlaggebend ist?

2. Willst Du behaupten die Ruhemasse der Kugel im Ruhesystem S' von Bob ändert sich durch die Beschleunigung?

3. Wenn nun ein gleichgroßer Impuls auf eine gleichgroße Ruhemasse wirkt, was soll da wohl anderes rauskommen als dasselbe?

So, da reicht echt die Logik und der ganz normale Verstand aus um das erkennen zu können.

Du behauptest aber, es würde einen Unterschied geben um die Kugel nun vor oder nach der Beschleunigung selber einen Impuls erhält. Dann erkläre doch mal, was da zu dem Unterschied führen soll, es kann nur nur die Ruhemasse der Kugel oder die Größe des Impulses auf die Kugel sein. Beides bleibt aber gleich.

Damit bist Du ganz einfach widerlegt.

Quod erat demonstrandum

@skagerak

Ja es geht um eine Uhr, @pluss hat behauptet, eine mechanische Uhr würde nicht dilatiert laufen. Nachdem man ihm einige Grundlagen der Physik und Mathematik vermittelt hatte, behauptete er dann aufmal, nur die nach der Beschleunigung gestartete Uhr würde dilatieren.

Dazu findet sich natürlich nichts im Internet oder der Fachliteratur, es heißt ja auch Zeitdilatation (ZD) und nicht "mechanische-Uhr-nach-der Beschleunigung-gestartet-und-nicht-mechanische-Uhr-Dilatation" (MUNDBGUNMUD). :D

Und an den ganzen Fragen von @pluss hier: Beitrag von pluss (Seite 88) kannst Du sehen, er versucht weiter abzulenken. Ist recht üblich bei Leuten die ihre Behauptungen nicht belegen können, widerlegt wurden, und nun einfach nicht in der Lage sind ihren Irrtum offen einzuräumen. Dann stellt man eben dem Gegenüber ganz viele Fragen.

So, und inzwischen versucht er auch nun über den Impuls das Ganze hier weiter tanzen zu können.

Fachlich ist das alles lange klar, über 100 Jahre schon.

@pluss

Ich finde es ja echt gut, dass Du nun versuchst Bildungslücken zu stopfen und mal die Dinge von Grund auf nachfragst, offenbar hast Du ja da wirklich noch vieles nicht verstanden, darum will ich mal helfen.

pluss schrieb:1. Was für Eigenschaften muss ein Zeitmesser erfüllen, um als "Uhr" im physikalischen Sinne zu gelten?

Er muss die SI-Sekunde lokal richtig messen.

Wikipedia: Sekunde
http://www.quantenwelt.de/einheiten/sekunde.html (Archiv-Version vom 11.02.2018)
https://www.ptb.de/cms/ptb/fachabteilungen/abt4/fb-44/ag-441/realisierung-der-si-sekunde/die-geschichte-der-zeiteinheit.html

---

pluss schrieb:2. Was versteht man unter physikalischer Zeit?

https://www.lernhelfer.de/schuelerlexikon/physik/artikel/zeit
Wikipedia: Zeit#Zeit als physikalische Größe
http://www.xn--relativittsprinzip-ttb.info/faq/was-ist-zeit.html
http://www.audretsch.uni-konstanz.de/activities/download/Die_physiklische_Zeit.pdf (Ruhig mehrfach lesen ...)

---

pluss schrieb:3. Existiert die physikalische Zeit bereits, und wir brauchen sie nur noch messen?
4. Oder produzieren wir diese Zeit erst?
5. Ist Zeit das, was eine Uhr anzeigt?

Siehe 2.

---

pluss schrieb:6. Wann geht die Uhr richtig?
7. Dann wenn ich die Zeit mit einer andere Uhr vergleiche?
8. Woher aber weiß ich, dass die zweite Uhr richtig oder falsch geht?

Siehe 1.

@skagerak

skagerak schrieb:Also geht es konkret darum, ob die Uhr dilatiert wenn sie nach der Beschleunigung gestartet wurde?

Es geht folgendes: Kugel 2 hat bereits eine y-GEschwindigkeit.

Die Kernfrage:

Wenn nun die Kugel mit der Vertikalgeschwindigkeit u_y = 0,7c, horizontal auf der x-Achse beschleunigt wird, was passiert mit der y-Geschwindigkeit u_y = 0,7c?

Bleibt die konstant, wird kleiner oder größer?

@pluss behauptet die y-Geschwindigkeit bleibe im nichtmitbeschleunigten Bezugssystem konstant. Das heißt während die Kugel immer schneller auf der x-AChse wird bleibt u_y konstrant. Dies sei auch der Grund dafür wieso eine Kugel mit einer Vertikalgeschwindigkeit u_y ≠ 0 nur auf eine bestimmte Horizontalgeschwindigkeit beschleunigt werrden kann.

Beipiel: u_{y_{Kugel~2}} = 0,99c



Übertragen wir das z.B. auf einen Laserstrahle. WEnn wir das nun für Licht (also ein Photon) anwenden wissen wir das das nicht sein kann. Ein Photon hat ja schon c, kann aber trotzdem horizontal beschleunigt werden. Da der Gesamtvekotor c erhalten bleiben muss, muss die y-Komponente vom Lichtstrahl kleiner werden. Die Folge daraus wäre Kugeluhren oder Ur-Uhren, gestartet vor der Beschleunigung gehen auch nach der Beschleunigung bei hoher Reltaivgeschwindigkeit nicht dilatiert, während Lichtuhren das machen.

Nun wie würde die Sache dann im horizontal mitbeschleunigten Bezugssystem aussehen?
Da aber gilt
Das heißt im mitbeschleunigten Bezugssystem, in dem die Kugel horizontal ruht, müsste die Kugel bei horizontaler Beschleunigung auch vertikal beschleunigen.

Übertragen auf das Bahnhof-Zug-Beipiel: Ein Kind sitze im Zug und hat einen Pendelball der hoch und runterspringt mit 0,5c.
@pluss Prämisse: Im nichtmitbeschleunigten Bezugssystem bleiben Geschwindigkeiten erhalten. Das heißt: WEnn der Zug losfährt und in relativistische GEschwindigkeiten kommt, würde die am Bahnhof bleibende, nichtmitbeschleunigte Person den Ball immer mit 0,5c hüpfen sehen. Der Junge der hingegen im Zug sitzt und horizontal zum Ball ruht würde merken wie sein Ball zunehmend schneller hüpft obwohl die Zugkraft horizontal ist.
Für den am Bahnhof stehenden: Würde der Junge seinen Ball mit 0,99c hüpfen lassen, könnte der Zug nicht schneller als 0,141c schnell werden, das heißt auch der im Zug sitzenden würde merken er kann nicht schneller gegenüber dem Bahnhof werden als 0,141c.

Wollte der Junge das der Zug nicht mehr starten kann, würde er den Ball mit 0,999999999999999999c hüpfen lassen. Das sind die Konsequenzen in Worte gefasst.

pluss schrieb:Sag mal willst du mich verarschen?
Was hätte ich denn statt 0,7c 0{,}7c 0,7c für einen Betrag nehmen sollen, vielleicht 0,815 0{,}815 0,815 ?

@pluss

Sind folgende Gleichungen richtig?

@pluss

Mein Ansatz ist folgender:




System 1 ist unser urspüngliches System. In diesem ist jedoch der Stoß nicht symmetrisch da die Geschwindigkeiten u_x und u_y schon nicht gleich sind. Man transformiert alos in das Ruhesystem der Kugeln mit den bekannten Transformationsformeln:

Wikipedia: Relativistisches Additionstheorem für Geschwindigkeiten#Definition

Man transformiert ins Ruhesystem der Kugel 2 (man könnte auch Kugel 1 wählen.). Da trägt den gesamten Impuls vor dem Stoß Kugel 1. Nun rotiert man noch das Koordinatensystem, dann liegen nämlich alle Gschwindigkeiten auf einer Achse. Hier ist das Problem symmetrisch und lässt sich einfach lösen den die Kugel 2 muss vor dem Stoß ruhen und nach dem Stoß muss Kugel 1 ruhen.

Wie man sieht hat man einen einfach 1-dimensionalen Stoß, den man mit folgenden Gleichungen lösen kann:

Wikipedia: Elastic collision#One-dimensional relativistic

mojorisin schrieb:Sind folgende Gleichung richtig?

Nein, ist als wenn einer Fragt:

mojorisin schrieb:Mein Ansatz ist folgender:

Meiner ein anderer, aber ist dir ja bekannt.
Zu was dein Ansatz führt, wirst du ja sicherlich noch feststellen.