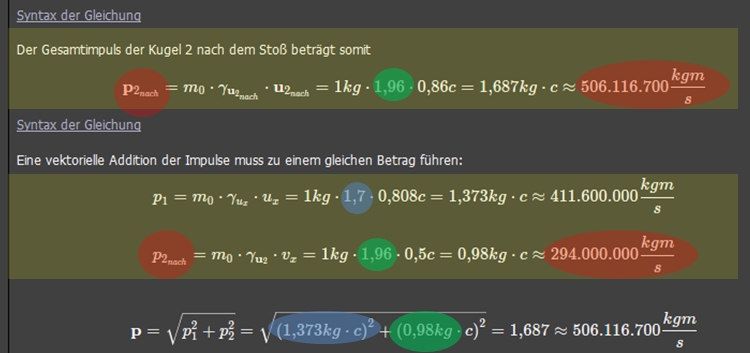
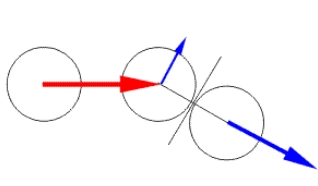
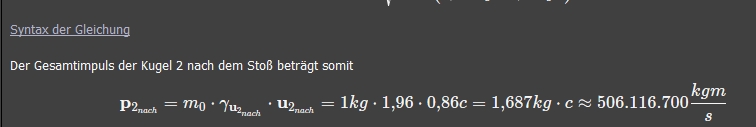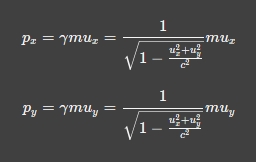@pluss Nun du berechnest ja hier:
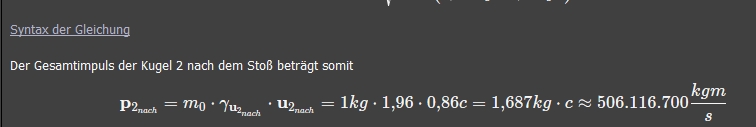 Beitrag von pluss (Seite 88)
Beitrag von pluss (Seite 88)genau die Gleichung nach oben genannten FOrmeln. Wieso ist das bei dir richtig bei mir aber falsch, bzw. Obstsalat?
Und wieso findet man bei Wikipedia exakt den Lorentzfakotor wie ich ihn in den Gleichugnen verwende?
 Wikipedia: Energy–momentum relation#Heuristic approach for massive particles
Wikipedia: Energy–momentum relation#Heuristic approach for massive particlesUNd wieso rechnest du manchmal exakt nach der Formel die ich gepostet habe, powboehl du sie aúgenscheinlich für falsch hälst:
 pluss schrieb am 08.02.2018:Den aus u=(ux,uy)\mathbf u= \left (u_x , u_y \right )u=(ux,uy), also zwangsweise den, der in deiner Impulsberechnung enthalten ist.
pluss schrieb am 08.02.2018:Den aus u=(ux,uy)\mathbf u= \left (u_x , u_y \right )u=(ux,uy), also zwangsweise den, der in deiner Impulsberechnung enthalten ist.
 pluss schrieb:Zu was dein Ansatz führt, wirst du ja sicherlich noch feststellen.
pluss schrieb:Zu was dein Ansatz führt, wirst du ja sicherlich noch feststellen.
Ganz konkret ist das Problem bei deinem Ansatz das sowohl der x als auch der der y-Impuls von der x- und der y-GEschwindigkeit abhäng.
Des Weiteren habe ich deine Resultate auf deren Impulserhaltung überprüft:
Gegeben:
(
INidzes: x,y: RIchtung; 1,2: Kugel; vS: vor Stoß; nS: nach Stoß)
Impulse vor dem Stoß:
---------------------------------------------------------------------------------
Kugel 1:
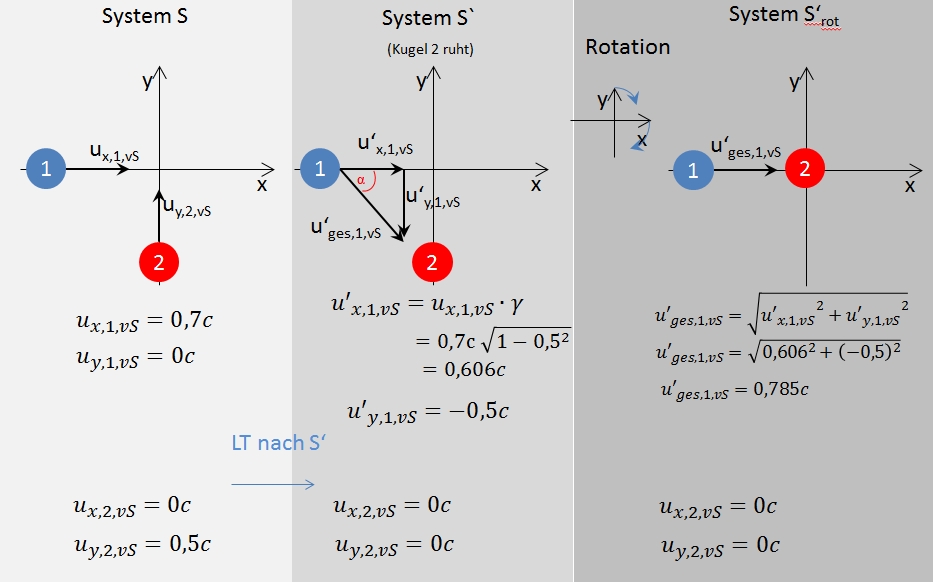
u_{x,1,vS} = 0,7c
u_{y,1,vS} = 0c
Impuls -->
p_{x,1,vS} = \gamma m u_x = \frac{1}{\sqrt{1-(0,7^2+0^2)}}\cdot 1~kg\cdot 0,7 = 0,9802kg\cdot c p_{y,1,vS} =0 Kugel 2:
u_{x,2,vS} = 0c
u_{y,2,vS} = 0,5c
Impuls -->
p_{x,2,vS} =0 p_{y,2,vS} = \gamma m u_x = \frac{1}{\sqrt{1-(0^2+0,5^2)}}\cdot 1~kg\cdot 0,5 = 0,577 kg\cdot c Gesamtimpuls:
p_{ges, vS} = \sqrt{0,98^2+0,577^2} kg\cdot c = 1,138 kg cdot c
-------------------------------------------------------------------------------------
Deine Lösungen ergeben:
Gschwindigkeiten nach dem Stoß für Kugel 1:
u_{x,1,nS} = 0c
u_{y,1,nS} = 0c
Geschwindigkeiten nach dem Stoß für Kugel 2:
u_{x,1,nS} = 0,606c
u_{y,1,nS} = 0,5c
--> Impulse:
p_{x,2,nS} = \gamma m u_x = \frac{1}{\sqrt{1-(0,606^2+0,5^2)}}\cdot 1~kg\cdot 0,606 = 0,9795 kg\cdot c p_{y,2,nS} = \gamma m u_y = \frac{1}{\sqrt{1-(0,606^2+0,5^2)}}\cdot 1~kg\cdot 0,606 = 0,808 kg\cdot c Gesamtimpuls:
p_{ges, vS} = \sqrt{0,9795^2+0,577^2} kg\cdot c = 1,2699kg cdot c
Fazit: Von deiner Lösung passen weder die Einzelimpulse noch die Gesamtimpulse zusammen.
PS: FOlgendes alles aus dem nichtbeschleunigten System (Bahnhof):
DIe y-Impulse können auch gar nicht zusammen passen. Vor dem Stoß hat Kugel 2 nur eine y-GEschwindigkeit daher kommt die gesamte "reltivistische Masse" von daher. Nach dem Stoß hatt die Kugel 2 bei dir diesselbe y-GEschwindigkeit, aber aufgrund der zusätzlichen x-GEschwindigkeit eine erhöhte Masse was automatisch zu einem höhrene Impuls in y-RIchtung führt als vor dem Stoß. DAs ist der Grund warum deine Annahme bei Beschleunigung in x-Richtung bleibe die y-Geschwindigkeit gleich falsch ist.
Hat eine Kugel im Zug eine bestimmte y-Geschwindigkeit und der Zug beschleunigt dann, nimmt aus Sicht des Bahnhofes die reltivistische Masse zu. Damit der IMpuls in y-Richtung erhalten bleibt, aus Sicht vom Bahnhof, muss die y-GEschwinidigkeit runtergehen. Das ist exakt das Beipiel mit der Eiskunstläuferein. DAs zeigen die Formeln der BEschleunigungstransformation usw.
Du kannst das ignorieren aber die Relität ist so. Beziogen auf deine Uhr. Mit zunehmender Relativgeschwindigkeit sieht der Beobahcer vom Bahnhof die Uhr im Zug dilatiert. Egal welche Uhr auch deine Kugeluhr.
PPS:
 pluss schrieb:So, das ist meine Vorstellung einer schlüssigen und nachvollziehbaren Lösung.
pluss schrieb:So, das ist meine Vorstellung einer schlüssigen und nachvollziehbaren Lösung.

Nachvollziehbare Lösung? WIe kommst du auf einen Lorentzfaktor von 1,7? Welche Komponenten stecken da drinne?
skagerak schrieb:Ja aber ich dachte ursprünglich ging es darum und nun darauf hinaus. Steht die Ermittlung nicht dann dafür, dass eine Uhr dilatiert oder eben nicht dilatiert?