Schwierigkeit der Längenkontraktion
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:01Das will ich ja:pluss schrieb:Noch einfacher wäre es natürlich wenn du einfach mal aufzeigst wie die Beträge für System SSS deiner Ansicht nach korrekt berechnet werden,
Aber deine Antwort da drauf:mojorisin schrieb:Ich mache jetzt ne Stichpunkliste und mal schauen ob du allen Argumenten zustimmen kannst:
Ich kann dir aber auch kurz erklären wieso ich die Sache aus Sicht von S' betrachten will. Ganz einfach deshalb weil ich die Geschwindigkeit uy aus Sicht von S nachdem die Kugel beschleunigt hat gar nicht weiß. Diese ist eine Unbekannte die ich nur über Lorentztransformation aus S' berechnen kann. Denn nur in S' kann ich Annahmen treffen die überprüfbar zu unseren bisher bekannten physikalischen Gesetzetn ist. Daher die Frage ob du den 4 Punkten zustimmst.pluss schrieb:Warum jetzt plötzlich von System S auf System S′ wenn noch null geklärt ist wie was in System S zu berechnen ist?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:03@pluss
Ich weiß auf was du hinaus willst: Meine Antwort: Ändert sich die Geschwindigkeit zwischen zwei Systemen ändert sich der Lorentzfaktor.pluss schrieb:Ändert sich der Impuls, wenn sich die Masse des Körpers ändert?
Ändert sich die Masse, wenn der Körper einen Impuls auf der xxx-Achse erhält?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:08Das ist ein Irrtum, ein System S' ist überhaupt nicht erforderlich zur Sachklärung.mojorisin schrieb:Ich kann dir aber auch kurz erklären wieso ich die Sache aus Sicht von S' betrachten will. Ganz einfach deshalb weil ich die Geschwindigkeit uy aus Sicht von S nachdem die Kugel beschleunigt hat gar nicht weiß. Diese ist eine Unbekannte die ich nur über Lorentztransformation aus S' berechnen kann.
Wenn du davon ausgehst das ein Körper seine Geschwindigkeit auf der y-Achse verändert, wenn ein Beschleunigung auf der x-Achse erfolgt, hat das null und nichts mit irgendwelchen anderen Bezugsystem zu tun.
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:18Ein Körper A bewegt sich im System S mit der Geschwindigkeit \mathbf u= \lbrace u_x=0, u_y=0{,}5c \rbracepluss schrieb:Das ist ein Irrtum, ein System S' ist überhaupt nicht erforderlich zur Sachklärung.
Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf u_x=0{,}7c beschleunigt wurde?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:20@pluss
Wie groß ist uy nach dem der Körper beschleunigt wurde?pluss schrieb:Wie sieht der Geschwindigkeitsvektor von AAA im System SSS aus, wenn der Körper auf der xxx-Achse auf ux=0,7cu_x=0{,}7cux=0,7c beschleunigt wurde?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:33Wenn du der Ansicht bist das sich der Geschwindigkeitsvektor u_y ändert, dann solltest du wissen welche physikalische Gesetzmäßigkeit dafür verantwortlich ist und auch die Gleichungen zur Lösung des Problems kennen. Aber nicht jemanden Fragen, der davon überzeugt ist das sich der Geschwindigkeitsvektor u_y nicht verändert, weil er nach durchforsten von 11 Fachbüchern zur SRT und ART, sowie 24 Werken aus der Fachliteratur über Mechanik und Kinetik nicht ansatzweise etwas finden konnte was darauf hinweist das deine Ansicht zutreffend sein könnte.mojorisin schrieb:Wie groß ist uy nach dem der Körper beschleunigt wurde?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:35@pluss

Unter deiner Annahme ist nun die einzige Unbekannte die Geschwindigkeit u'y. Das ist die Geschwindigkeit im System S' das mit der Kugel mitbeschleunigt wurde. Nun wenn deine Annahme stimmt können wir nun anhande der Lorentztransformation in das Ruhesystem deiner Uhr zurückrechnen und können u'y bestimmen.
Wir nehmen die bekannte Formel:
Da u'x = 0 ist können wir einfac h umstellen nach u'y und erhalten:
Daraus ergänzt sich die Tabelle:
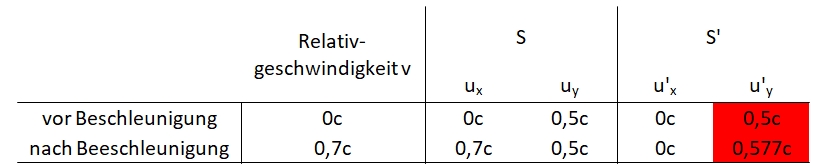
Wir sehen wenn uy kosntant bleiben soll dann mus sich u'y erhöhen. Siehst du einen Fehler in dieser Berechung?
Nun S' ist aber das Ruhesystem deiner Uhr. Natürlich ist das Ruhesystem erforderlich zur Sachklärung.pluss schrieb:Das ist ein Irrtum, ein System S′ ist überhaupt nicht erforderlich zur Sachklärung.
Nun denn schauen wir uns ann was passiert wenn deine Annahme zutrifft das uy konstan bleibt:pluss schrieb:Wenn du davon ausgehst das ein Körper seine Geschwindigkeit auf der y-Achse verändert, wenn ein Beschleunigung auf der x-Achse erfolgt, hat das null und nichts mit irgendwelchen anderen Bezugsystem zu tun.

Unter deiner Annahme ist nun die einzige Unbekannte die Geschwindigkeit u'y. Das ist die Geschwindigkeit im System S' das mit der Kugel mitbeschleunigt wurde. Nun wenn deine Annahme stimmt können wir nun anhande der Lorentztransformation in das Ruhesystem deiner Uhr zurückrechnen und können u'y bestimmen.
Wir nehmen die bekannte Formel:
u_y = u'_y \frac{1}{\gamma\left( 1+ \frac{u'_x v }{c^2} \right)}
Da u'x = 0 ist können wir einfac h umstellen nach u'y und erhalten:
u'_y = \gamma u_y = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} u_x = \frac{1}{\sqrt{1-\frac{0,5^2c^2}{c^2}}} u_x = 0,577 c
Daraus ergänzt sich die Tabelle:

Wir sehen wenn uy kosntant bleiben soll dann mus sich u'y erhöhen. Siehst du einen Fehler in dieser Berechung?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:42Wozu hat sich Hendrik Antoon Lorentz so abgestrampelt?mojorisin schrieb:Da u'x = 0 ist können wir einfac h umstellen nach u'y und erhalten:
Vielleicht um uns mit der Lorentz-Transformation zu beglücken?
Also ich würde einfach die Lorentz-Transformation anwenden um den Betrag des Vektors u_y' zu erhalten. Oder spricht etwas dagegen?
Schwierigkeit der Längenkontraktion
07.02.2018 um 23:48@pluss
Ja, es brauch keinen Betrag, was ich gerechnet habe ist die Standard Lorentztransformation für Geschwindigkeiten. Wenn du im System S die Vertikalgeschwindigkeit der beschleunigten Kugel festnagelst dann ist die Konsequenz das die Kugel im Ruhesystem S' beschleunigt werden muss. Daher erhälst du auch immer Zuwächse des Impulses, denn eine Zunahme der Vertikalgeschwindigkeit im mitbeschleunigtren System in dem Die Kugel horizontal "ruht" kann nur durch eine aktive Beschleunigung erfolgen, also eine Kraftaufwendung.pluss schrieb:Also ich würde einfach die Lorentz-Transformation anwenden um den Betrag des Vektors uy′u_y'uy′ zu erhalten. Oder spricht etwas dagegen?
Schwierigkeit der Längenkontraktion
08.02.2018 um 00:02Bitte @mojorisin, ich habe hier nachvollziehbar vorgerechnet wie ich zu den Beträgen (Geschwindigkeitsvektoren, Impuls und Energie) gelangt bin. Also behaupte nicht nur einfach meine Darstellungen sind fehlerbehaftet, sondern Zeige die Fehler explizit auf, und vor allem zeige auf wie es aus deiner Sicht korrekt berechnet wird.mojorisin schrieb:Ja, es brauch keinen Betrag, was ich gerechnet habe ist die Standard Lorentztransformation für Geschwindigkeiten. Wenn du im System S die Vertikalgeschwindigkeit der beschleunigten Kugel festnagelst dann ist die Konsequenz das die Kugel im Ruhesystem S' beschleunigt werden muss. Daher erhälst du auch immer Zuwächse des Impulses, denn eine Zunahme der Vertikalgeschwindigkeit im mitbeschleunigtren System in dem Die Kugel horizontal "ruht" kann nur durch eine aktive Beschleunigung erfolgen, also eine Kraftaufwendung.
Was erwartest du noch von mir, reicht es nicht wenn ich lückenlos aufzeige wie ich was berechnet habe?
Was muss ich noch liefern?
Wann lieferst du mal deine Berechnung zu System S und vielleicht auch S'?
Schwierigkeit der Längenkontraktion
08.02.2018 um 02:35Bitte sehr:pluss schrieb:Wann lieferst du mal deine Berechnung zu System SSS und vielleicht auch S′S'S′?

Ich habe jetzt mal meinen Ansatz (obere Hälfte, u'y konstant) und deinen Ansatz (untere Hälfte, uy konstant) verglichen und berechnet wie sich die IMpulse unter den Annahmen verhalten:
In der oberen Hälfte sind alle Werte berechnet unter der Annahme das u'y konstant ist, d.h. in der Spalte u'y sind die WErte 0,5c händisch eingetragen, von da ausgehende werden alle anderen Werte berechnet.
In der unteren Hälfte sind alle Werte berechnet unter der Annahme das uy konstant ist, d.h. in der Spalte uy sind die Werte 0,5c händisch eingetragen, von da ausgehende werden alle anderen Werte berechnet.
Für die Geschwindigkeiten wurde jeweils der Lorentzfaktor zwischen den Systemen berechnet also:
LF S-S':
\gamma_{LF~S-S'} = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}
dann berechnet sich in der oberen Tabelle uy wie folgt:
u_y = \frac{u'_y}{\gamma_{LF~S-S'}}
in der unteren Tabelle errechnet sich u'y ähnlich:
u'_y = u_y\gamma_{LF~S-S'}
Für die Impulse wurde der Gammafaktor anhand der Gesamtgeschwindigkeit berechnet:
LF Impuls:
\gamma_{LF~Impuls} = \frac{1}{\sqrt{1-\frac{u^2_x + u^2_y}{c^2}}}
Hier die Excel Datei:
Dateianhang: SRT.xlsx (34 KB)
Folgende Punkte fallen auf:
- Im oberen Fall ist die Kraft in y-Richtung Fy = 0, da sich der IMpuls in y-Richtung nicht ändert.
- Im unteren Fall ergibt sich eine Kraft in y-Richtung Fy da sich der IMpuls auf der y-Achse ändert
- Im unteren Fall: Der Impuls in y-Richtung ändert sich da die y'-Geschwindigkeit u'y im beschleunigten System zunehmen muss, damit im ruhenden System S die Geschwinidigkeit uy gehalten werden kann. Dies entspricht einer realen aktiven Kraft
- Die Gesamtenergie und der Gesamtimpuls ist im oberen Fall im beschleunigten System S' erhalten. Das macht auch Sinn da sich dort die Geschwindigkeit der Kugel nicht ändert. Weiters macht das Sinn im Hinblick auf das Äquivalenzprinzip. Jemand der mitsamt der Rakete beschleunigt kann nicht unterscheiden ob er auf der Erde ist oder sich in einer beschleunigten Rakete befindet. Aus Erfahrung wissen wir das Sachen nicht von alleine senkrecht zur Gravitation beschleunigen
- Im unteren Fall nimmt die Gesamtenergie aus Sicht von beiden Systemen zu. Im System S' kann die kinetische Energie nur auf der y'-Achse zunehmen, da dieses System ja mitsamt der Kugel beschleunigt wird und somit u'x konstant 0 ist.
- Das Wichtigste worauf eigentlcih die ganze Diskussion sich beruft: u'y und uy laufen in beiden Fällen auseinander. Da uy und u'y die Taktfrequenzgeber der Ur-Uhr sind laufen die Uhren in beiden Fällen auseinander, was deine ursprüngliche These ein Uhr würde, gestartet vor Beschleunigung, nicht der Zeitdilatation unterliegen widerlegt.
@pluss
Dein Fehler ist das du die Geschwindigkeit nicht aus dem Ruhesystem der Kugel bzw. der Uhr festhalten willst sondern aus einem System das sich relativ dazu bewegt bzw. nicht mitbeschleunigt wird. Aus diesem System S heraus betrachtet nimmt mit zunehmender Beschleunigung der Kugel jedoch die Relativgeschwindigkeit zu und somit ändert sich laufend der Lorentzfaktor. Das aus horizontal beschleungten Systemen für einen ruhenden Beobachter eine orthogonale Beschleunigung hervorgeht, zeigt sich jedoch in deinem Buch dessen Formeln du bereits verlinkt und den Wiki-Links die ich gebracht habe. Leider ignorierst du diese Herleitungen.
Generell noch: Die Annahme einer konstanten GEschwindigkeit macht physikalscih nur Sinn im Bezugssystem eines Objektes, denn dort ändert sich eine Geschwindigkeit nicht weil die Relativgeschwindigkeit logischerweise konstant = 0 ist. Sehe ich ein Objekt horizontal an mir vorbeifliegen mit zunehmender GEschwindigkeit kann ich nicht davon ausgehen das die damit verbundenen Vertikalgeschwindigkeiten konstant bleiben. Ganz einfach deswegen:
u_y = \frac{\Delta y}{\Delta t} = \frac{\Delta y'}{\Delta t' \gamma}
Das heißt uy hängt vom Lorentzfaktor ab und damit von der Relativgeschwindigkeit zwischen mir und dem Objekt. Nimmt jedoch die Geschwindigkeit zwischen mir und einem Objekt zu und ich nehme an uy bleibt konstant, gehe ich implizit davon aus das der Lorentzfaktor bei Beschleunigung konstant bleibt, was ja wohl keinen Sinn macht.
Schwierigkeit der Längenkontraktion
08.02.2018 um 06:35Hmm das hab ich hier doch schon vor Monaten fast exakt so gelesen.pluss schrieb:Bitte @mojorisin, ich habe hier nachvollziehbar vorgerechnet wie ich zu den Beträgen (Geschwindigkeitsvektoren, Impuls und Energie) gelangt bin. Also behaupte nicht nur einfach meine Darstellungen sind fehlerbehaftet, sondern Zeige die Fehler explizit auf, und vor allem zeige auf wie es aus deiner Sicht korrekt berechnet wird.
@mojorisin
Schon faszinierend wieviel Geduld du hast, wo das Spiel doch jetzt gerade wieder von vorne los geht :)
Schwierigkeit der Längenkontraktion
08.02.2018 um 11:18@McMurdo
DAs korrekt Vorgehen muss also so sein:
Zuerst bestimmt man alle Geschwindigkeitskomponenten eines Objektes in dem System (z.B. im System S) in dem man den Impuls des Objektes bestimmen will. WEnn man nur Geschwindigkeitswerte aus einem anderen System hat (z.B. aus System S'), muss man zuerst alle Geschwindigkeitskomponenten des Objektes in S ermitteln. Daraus kann man dann den Lorentzfaktor bzw die Relativgeschwindigkeit ermitteln der zwischen dem Objekt selbst und dem System S herrscht. Ich hab das lange falsch gemacht bzw. nicht richtig verstanden, jetzt schon :)
@pluss
Die Überschriften in der Tabelle sollen nicht heißen "Annahme u'x = const." bzw. "Annahme ux = const." sondern natürlich "Annahme u'y = const." bzw. "Annahme uy = const."
Immer und immer wieder lernt man selber dazu. Z.B. war habe ich den Lorentzfaktor für den Impuls immer falsch berechnet indem ich immer den Lorentzfaktor eingesetzt habe der zwischen zwei Systemen vorherrscht. Für die korrekte Impulsbetrachtung muss ich aber direkt mit dem Ruhesystem des Objektes vergleichen. Im oberen fdall ist das wahre Ruhesystem der Kugel also nicht S' oder S sondern das wo die Kugel in alle Richtungen ruht.McMurdo schrieb:Schon faszinierend wieviel Geduld du hast, wo das Spiel doch jetzt gerade wieder von vorne los geht :)
DAs korrekt Vorgehen muss also so sein:
Zuerst bestimmt man alle Geschwindigkeitskomponenten eines Objektes in dem System (z.B. im System S) in dem man den Impuls des Objektes bestimmen will. WEnn man nur Geschwindigkeitswerte aus einem anderen System hat (z.B. aus System S'), muss man zuerst alle Geschwindigkeitskomponenten des Objektes in S ermitteln. Daraus kann man dann den Lorentzfaktor bzw die Relativgeschwindigkeit ermitteln der zwischen dem Objekt selbst und dem System S herrscht. Ich hab das lange falsch gemacht bzw. nicht richtig verstanden, jetzt schon :)
@pluss
Die Überschriften in der Tabelle sollen nicht heißen "Annahme u'x = const." bzw. "Annahme ux = const." sondern natürlich "Annahme u'y = const." bzw. "Annahme uy = const."
Schwierigkeit der Längenkontraktion
08.02.2018 um 14:04Ich bin kein Pawlowscher Hund der über eindeutige Flüchtigkeitsfehler herfällt.mojorisin schrieb:Die Überschriften in der Tabelle sollen nicht heißen "Annahme u'x = const." bzw. "Annahme ux = const." sondern natürlich "Annahme u'y = const." bzw. "Annahme uy = const."
Was mir aber aufgefallen ist, die Gesamtenergie im System S ist widersprüchlich. Mir fehlt momentan die Zeit (heute Abend werde ich es ausführlich aufzeigen), aber mach dir mal darüber Gedanken:
E=m \cdot c^2=m_0 \cdot \gamma_\mathbf u \cdot c^2= \sqrt {E_0^2+ \left ( \mathbf p + c \right )^2}
Schwierigkeit der Längenkontraktion
08.02.2018 um 14:24@pluss
Diese Formel:
ist jedoch falsch. Wenn dann gilt:
"p + c" geht nicht, ein Impuls kann nicht mit der LG addiert werden, da stimmen die Einheiten schon nicht.
Ich bin gespannt.pluss schrieb:Was mir aber aufgefallen ist, die Gesamtenergie im System S ist widersprüchlich.
Diese Formel:
E = \sqrt{E_0^2 + (p + c)^2}
ist jedoch falsch. Wenn dann gilt:
E = \sqrt{E_0^2 + (pc)^2}
"p + c" geht nicht, ein Impuls kann nicht mit der LG addiert werden, da stimmen die Einheiten schon nicht.
Schwierigkeit der Längenkontraktion
08.02.2018 um 14:24@mojorisin
Beträge aus System S , Reihe 12 der oberen Tabelle:
Über die letzte Gleichung erhält man eine deutlich geringere Energie. Der Fehler kann nur aus dem Gesamtimpuls begründet werden, denn alle anderen Werte wie Ruhenergie des Körpers und c bedürfen sicherlich keiner Diskussion.
Beträge aus System S , Reihe 12 der oberen Tabelle:
E=m_0 \cdot \gamma_\mathbf u \cdot c^2= 1kg \cdot 1{,}6169 \cdot 300{.}000{.}000 \left (\frac {m} {s} \right )^2=1{,}46 \cdot 10^{17}J
E= \sqrt {E_0^2+ \left ( \mathbf p \cdot c \right )^2}= \sqrt {\left (9{,}0 \cdot 10^{16}J \right )^2+ \left ( 381{.}174{.}600 \frac {kgm} {s} \cdot 300{.}000{.}000 \frac m s \right )^2}=1{,}14 \cdot 10^{17}J
Über die letzte Gleichung erhält man eine deutlich geringere Energie. Der Fehler kann nur aus dem Gesamtimpuls begründet werden, denn alle anderen Werte wie Ruhenergie des Körpers und c bedürfen sicherlich keiner Diskussion.
Schwierigkeit der Längenkontraktion
08.02.2018 um 14:30Ja, Flüchtigkeitsfehler beim erstellen in Latex, gerechnet habe ich mit \mathbf p \cdot cmojorisin schrieb:ist jedoch falsch. Wenn dann gilt:
Schwierigkeit der Längenkontraktion
08.02.2018 um 14:32Welche Lorentzfaktoren nutzt du in der zweiten Gleichung?pluss schrieb:Ja, Flüchtigkeitsfehler beim erstellen in Latex, gerechnet habe ich mit p⋅c\mathbf p \cdot cp⋅c
S im oberen Fall oder S im unteren Fall?pluss schrieb:Was mir aber aufgefallen ist, die Gesamtenergie im System S ist widersprüchlich.
Können wir uns darauf einigen in c zu rechnen? Sonst müssen wir ständig aller Ergebnisse von ineinander umrechenen.
Schwierigkeit der Längenkontraktion
08.02.2018 um 14:34Den aus \mathbf u= \left (u_x , u_y \right ), also zwangsweise den, der in deiner Impulsberechnung enthalten ist.mojorisin schrieb:Welche Lorentzfaktoren nutzt du in der zweiten Gleichung?
