Schwierigkeit der Längenkontraktion

pluss schrieb:Schon möglich das ich einen Knoten in den Gedanken habe. Dann helfe mir doch bitte ihn zu lösen.

Ich schrieb doch schon das die die Zeitdilatation und die Längenkontraktion der Konstanz der Lichtgeschwindigkeit geschuldet sind und nicht den verwendeten Uhren.

pluss schrieb:1. Wie viele Perioden hat die Uhr aus Sicht von Alice nach 1 s ihrer Eigenzeit durchlaufen?
2. Wie viele Perioden hat die Lichtuhr aus Sicht von Alice nach 1 s ihrer Eigenzeit durchlaufen?

Beide Uhren gehen um denselben Betrag langsamer für Alice, wenn sie sich beide mit 0.9c relativ zu ihr bewegen.

McMurdo schrieb:Beide Uhren gehen um denselben Betrag langsamer für Alice, wenn sie sich beide mit 0.9c relativ zu ihr bewegen.

Also ist meine Berechnung falsch?
Wo genau liegt da der Fehler?

P.S.: Und danke das du mir hilfst den Konten zu lösen.

pluss schrieb:Also ist meine Berechnung falsch?
Wo genau liegt da der Fehler?

Ich bin kein Mathematik-Experte aber so wie ich das sehe hast du da mit dem Satz des Pythagoras versucht irgendeine Geschwindigkeit des Pendels auszurechnen. Du musst aber berechnen wie Alice das an ihr vorbeifliegende Pendel sieht. Denn das Pendel legt aus ihrer Sicht eine längere Strecke zurück als das Pendel einer zu ihr unbewegten Uhr. Da die LG konstant ist, vergehen daher die Sekunden der bewegten Uhr für Alice langsamer.

McMurdo schrieb:Du musst aber berechnen wie Alice das an ihr vorbeifliegende Pendel sieht. Denn das Pendel legt aus ihrer Sicht eine längere Strecke zurück als das Pendel einer zu ihr unbewegten Uhr.

Das ist korrekt und habe ich auch in den Berechnungen über den Satz des Pythagoras berücksichtigt.

McMurdo schrieb:Da die LG konstant ist, vergehen daher die Sekunden der bewegten Uhr für Alice langsamer.

Der erste Teilsatz ist natürlich korrekt. Der zweite nur unter bestimmten Bedingungen, nämlich dann wenn die Geschwindigkeit des Teilchens, welche über die zurückgelegte Wegstrecke des Teilchens und der Periodendauer der Uhr ermittelt werden kann, größer als LG ist. Das trifft in meinem Beispiel jedoch nachweislich nur auf die Lichtuhr zu.

Die Resultate meiner Lichtuhr kritisiert ihr nicht, nur die meiner Beispieluhr. Folglich können wir uns auf diese beschränken.
Darum frage ich nochmals, wo konkret liegt der Fehler in den Berechnungen zu dieser Uhr?

@McMurdo

Die Lichtuhr selber ist ja gegessen, geht um diese "Ur-Uhr", klar geht die, wenn sie denn eine richtige Uhr ist, wie die Lichtuhr für Alice langsamer. Mal grob eine Richtung, das Teilchen der Ur-Uhr ist im System von Bob (nenne ich mal so) bewegt und bekommt in diesem System eine Geschwindigkeit zugeordnet.

Dort wird also die Länge und Zeit gemessen.

Im System von Alice kommt nun eine Geschwindigkeit dazu ...



@pluss

Gut mal einen Denkanstoß, setzte die Geschwindigkeit Deines Teilchens im System Bob mal auf 0.9 c und lasse dann die Ur-Uhr ebenfalls mit 0.9 c an Alice vorbeifliegen. Rechne doch mal mit Deiner Methode die Geschwindigkeit des Teilchens der Ur-Uhr für Alice aus. Und sage dann mal, ob das so möglich ist.

Ich denke mal das könnte helfen.

nocheinPoet schrieb:Gut mal einen Denkanstoß, setzte die Geschwindigkeit Deines Teilchens im System Bob mal auf 0.9 c und lasse dann die Ur-Uhr ebenfalls mit 0.9 c an Alice vorbeifliegen. Rechne doch mal mit Deiner Methode die Geschwindigkeit des Teilchens der Ur-Uhr für Alice aus.

300.000.000 m/s

nocheinPoet schrieb:Und sage dann mal, ob das so möglich ist.

Klar ist das so möglich.

@pluss

Ich gebe die Geschwindigkeiten in c an und Du in m/s? Warum nicht in c? Dann schaue mal hier:
http://www.mathematik-wissen.de/addition_von_vektoren.htm (Archiv-Version vom 01.07.2017)

Gegeben sind zwei Geschwindigkeitsvektoren, jeder mit einem Betrag von 0.9 c gesucht ist nun der Betrag des Ergebnisvektors. Rechnest Du klassisch nach Newton solltest Du so rechnen:

√((0.9 c)² + (0.9 c)²) = 1.277 c

Und möglich?

Anders, eventuell kommst Du dann darauf, die Ur-Uhr fliegt nicht seitlich an Alice vorbei, sondern mit 0.9 c auf Alice zu, das Teilchen in der Ur-Uhr bewegt sich dabei auch gerade auf Alice zu, also nach unten.

Dann liegen beide Vektoren in derselben Richtung, klassisch gerechnet wäre das:

0.9 c + 0.9 c = 1.8 c

Und läuten denn nun die Glocken?

Nebenbei bekomme ich da für die erste Rechnung 423.970.560 m/s und nicht 300.000.000 m/s raus.

nocheinPoet schrieb:Gegeben sind zwei Geschwindigkeitsvektoren, jeder mit einem Betrag von 0.9 c gesucht ist nun der Betrag des Ergebnisvektors. Rechnest Du klassisch nach Newton solltest Du so rechnen:

Bei relativistischen Geschwindigkeiten rechnet man so aber nicht, sondern wendet das Relativistische Additionstheorem an:

nocheinPoet schrieb:Ich gebe die Geschwindigkeiten in c an und Du in m/s? Warum nicht in c?

Was soll denn die korinthenkackerei?
Dann eben 1c wenn du dich an 300.000.000 m/s störst.

@pluss

pluss schrieb:Bei relativistischen Geschwindigkeiten rechnet man so aber nicht, sondern wendet das Relativistische Additionstheorem an: ...

Es wird doch, wobei Deine Formel doch wo seltsam ist. Wie findest Du denn diese hier:

u = (u' + v) / (1 + u' * v/c²)

Da ich c gerne 1 setzte dann:

u = (u' + v) / (1 + u' ⋅ v)

Geschwindigkeiten sind dann in c gemessen. So, nun ist das ja ganz nett, diese Gleichung geht aber davon aus, dass beide Geschwindigkeiten in dieselbe Richtung liegen, bei der Ur-Uhr ist das ja nun anders.

@pluss

So, eben noch mal gesucht und ein nettes Beispiel gefunden, schaue es Dir mal an:
http://physikunterricht-online.de/jahrgang-12/addition-von-geschwindigkeiten/

nocheinPoet schrieb: wobei Deine Formel doch wo seltsam ist.

Ist sie falsch?
Wenn nicht, was soll deine unnötige Rhetorik dann.

nocheinPoet schrieb:So, nun ist das ja ganz nett, diese Gleichung geht aber davon aus, dass beide Geschwindigkeiten in dieselbe Richtung liegen, bei der Ur-Uhr ist das ja nun anders.

Das nichts schneller als Licht sein kann stellt wohl keiner infrage. Folglich bräuchte man nicht einmal den Taschenrechner bemühen um deine Frage zu beantworten.

@pluss

pluss schrieb:Ist sie falsch? Wenn nicht, was soll deine unnötige Rhetorik dann.

Natürlich ist das

nicht das Relativistische Additionstheorem, Du willst doch zwei Geschwindigkeiten addieren, wo willst Du die da eingeben? Bedenke mal, c ist eine Konstante, also v und dann?

Und in der Regel hat eine Gleichung ein Gleichheitszeichen, Du hast da nur einen Term hingeschrieben.

pluss schrieb:Das nichts schneller als Licht sein kann stellt wohl keiner infrage. Folglich bräuchte man nicht einmal den Taschenrechner bemühen um deine Frage zu beantworten.

Gut, freut mich ja, wenn Du meinst so klare Dinge kann man als gegeben nehmen und musst diese nicht weiter hinterfragen. Schade dass dieses so nicht bei anderen Dingen ebenso funktioniert.

So, mal konkret, ich hatte Dir ja schon gesagt, dass ich den Beitrag: Beitrag von pluss (Seite 6) unklar finde. Kannst Du ja gar nicht nachvollziehen, wie auch immer, magst Du mal eben zeigen und hier wiederholen, wo Du da die Geschwindigkeit des Teilchens der Ur-Uhr für Alice relativistisch richtig addiert hast, also richtig berechnet?

pluss schrieb:zweite nur unter bestimmten Bedingungen, nämlich dann wenn die Geschwindigkeit des Teilchens, welche über die zurückgelegte Wegstrecke des Teilchens und der Periodendauer der Uhr ermittelt werden kann, größer als LG ist. Das trifft in meinem Beispiel jedoch nachweislich nur auf die Lichtuhr zu.

Und dann dies:

pluss schrieb:Das nichts schneller als Licht sein kann stellt wohl keiner infrage.

Kann ja dann irgendwie nicht stimmen mit der Uhr. Beide Uhren können ihre Information über die Dauer ihrer Pendelperiode nur mit max. LG übertragen. Und wenn sie mit 0.9c an dir vorbei fliegt dauert geht die Uhr langsamer da die Information über die Dauer einer Periode einen längeren Weg zurücklegen muss, immer.

nocheinPoet schrieb:So, mal konkret, ich hatte Dir ja schon gesagt, dass ich den Beitrag: Diskussion: Schwierigkeit der Längenkontraktion (Beitrag von pluss) unklar finde.

Worauf ich eingegangen bin: Beitrag von pluss (Seite 7)
Wenn ich Unklarheiten deinerseits beseitigen soll, solltest du sie schon konkret benennen.

nocheinPoet schrieb:magst Du mal eben zeigen und hier wiederholen, wo Du da die Geschwindigkeit des Teilchens der Ur-Uhr für Alice relativistisch richtig addiert hast, also richtig berechnet?

Hättest du mein posting mit dem Gedankenexperiment gelesen, würdest du die Frage nicht stellen. Aber bitte, für dich wiederhole ich mich natürlich gern:

McMurdo schrieb: pluss schrieb:
zweite nur unter bestimmten Bedingungen, nämlich dann wenn die Geschwindigkeit des Teilchens, welche über die zurückgelegte Wegstrecke des Teilchens und der Periodendauer der Uhr ermittelt werden kann, größer als LG ist. Das trifft in meinem Beispiel jedoch nachweislich nur auf die Lichtuhr zu.

Und dann dies:

pluss schrieb:
Das nichts schneller als Licht sein kann stellt wohl keiner infrage.

Sorry, gebe zu mich unklar ausgedrückt zu haben. Sollte besser "theoretisch größer als LG ist" heißen.
Wo du da einen Widerspruch siehst ist mir nicht ganz klar. Hatte die Bedingung doch genannt:

@pluss

pluss schrieb:

nocheinPoet schrieb:magst Du mal eben zeigen und hier wiederholen, wo Du da die Geschwindigkeit des Teilchens der Ur-Uhr für Alice relativistisch richtig addiert hast, also richtig berechnet?

Hättest du mein posting mit dem Gedankenexperiment gelesen, würdest du die Frage nicht stellen. Aber bitte, für dich wiederhole ich mich natürlich gern:

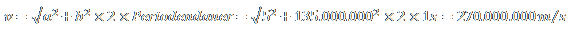
Du ich habe den gelesen. So, da hast Du nun einfach nur den Pythagoras genommen. Und auch wieder alles unklar, wo kommt die 5 her und wo die 135.000.000?

Also, bei Dir sieht es so aus:


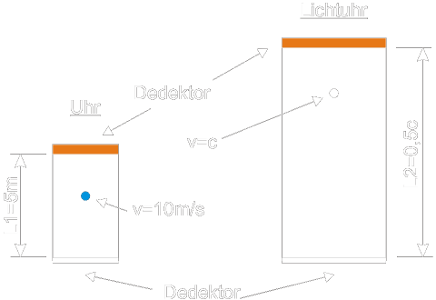
Da hast Du L1 = 5 m, ganz klar eine Länge und auf der anderen Seite hast Du L2 = 0,5 c, das ist aber eine Geschwindigkeit und keine Länge. Also da stimmt offenkundig schon mal etwas nicht.

Nun rechnest Du da mit dem Pythagoras und nimmst 5 und 135.000.000 und bekommst dann eine Geschwindigkeit raus.



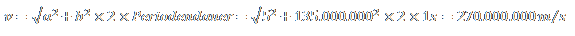
Konkret multiplizierst Du das Ergebnis aus dem Pythagoras mit 2 und dann noch mit 1 s und bekommst am Ende eine Geschwindigkeit raus, da ist die Einheit nun mal m/s. Irgendwie passt da wohl was mit Deinen Einheiten in der Gleichung nicht.

Welche Einheiten sollen den 5 und 135.000.000 haben, wenn Du da etwas nimmst und mit 1 s multiplizierst, dann sollte dieses Etwas die Einheit m/s² haben, wäre also eine Beschleunigung. Denn m/s² ⋅ 1 s = m/s oder?  
 
Wo kommen denn nun die 5 und die 135.000.000 überhaut her, warum steht da nichts im Bild und sonst wo im Beispiel von Dir? Eine 5 findet sich da nur links als Länge, die Geschwindigkeit für das Teilchen gibst Du mit 10 m/s an.

Eventuell wird nun klar, wo die Beschreibung Deines Gedankenexperimentes unklar wirken könnte.

Und dann fragte ich ja nach der relativistischen Addition, Pythagoras ist da ja nun doch was anderes. Hast Du denn nun mal nachgelesen und das hier:



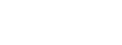
verstanden?

pluss schrieb:Sorry, gebe zu mich unklar ausgedrückt zu haben. Sollte besser "theoretisch größer als LG ist" heißen.
Wo du da einen Widerspruch siehst ist mir nicht ganz klar. Hatte die Bedingung doch genannt:

Es kann auch nicht theoretisch größer als LG sein. Nimm zb die Strecke des Pendels deiner Uhr. Die hast du ja mit 5m angegeben und das Pendel bewegt sich mit 10m/s. Also vergehn bei ruhender Uhr eine Pendelbewegung = 1 Sek. = 10m . Richtig? Das Pendel pendelt immer senkrecht.
Und nun bewege die Uhr und trage die bewegung des Pendels ab. Es entsteht wie in deinem Bild ein Dreieck. Die Strecke die das Pendel aber jetzt zurücklegen muss um einmal hin und her zu pendeln ist nun länger. Da es aber weiterhin mit 10m/s schwingt braucht es zwangsläufig länger für die längere Strecke, ergo geht die Uhr langsamer, da die uhr ja immer erst nach vollendung einer Pendelperiode um 1Sekunde weiterspringt.
So erstmal ganz einfach dargestellt und ohne groß rechnen zu müssen.

nocheinPoet schrieb:Du ich habe den gelesen. So, da hast Du nun einfach nur den Pythagoras genommen. Und auch wieder alles unklar, wo kommt die 5 her und wo die 135.000.000?

Die 5, hast du ja erkannt, was auch absolut unmissverständlich aus meiner Grafik hervorgeht, ist die Strecke vom Dedektor bis zum Spiegel. Die 135.000.000m entsprechen der Hälfte der zurückgelegten Strecke, die die Uhr bei einer gleichförmig geradlinigen Bewegung mit 90% der Lichtgeschwindigkeit zurücklegen würde (in der Grafik als "x" zu erkennen).

nocheinPoet schrieb:Da hast Du L1 = 5 m, ganz klar eine Länge und auf der anderen Seite hast Du L2 = 0,5 c, das ist aber eine Geschwindigkeit und keine Länge. Also da stimmt offenkundig schon mal etwas nicht.

Ja da hast du recht, das ist ein Fehler meinerseits. Zwar dürfte klar sein das damit eine Länge von 150.000.000m gemeint sein dürften, aber gut, man kann sich natürlich auch an Nichtigkeiten stören.

nocheinPoet schrieb:Konkret multiplizierst Du das Ergebnis aus dem Pythagoras mit 2 und dann noch mit 1 s und bekommst am Ende eine Geschwindigkeit raus, da ist die Einheit nun mal m/s. Irgendwie passt da wohl was mit Deinen Einheiten in der Gleichung nicht.

Was passt da nicht?
Bei "Meter x Sekunde" erhält man für gewöhnlich die Einheit m/s.

McMurdo schrieb: Da es aber weiterhin mit 10m/s schwingt braucht es zwangsläufig länger für die längere Strecke

Nein, es braucht nicht Länger. Das Teilchen ändert seine Geschwindigkeit, schließlich wird die Uhr bewegt und somit auch das Teilchen. Diese Geschwindigkeitsänderung hängt eben von der Bewegung der Uhr ab.

@pluss

pluss schrieb:Die 5, hast du ja erkannt, was auch absolut unmissverständlich aus meiner Grafik hervorgeht, ist die Strecke vom Dedektor bis zum Spiegel. Die 135.000.000m entsprechen der Hälfte der zurückgelegten Strecke, die die Uhr bei einer gleichförmig geradlinigen Bewegung mit 90% der Lichtgeschwindigkeit zurücklegen würde (in der Grafik als "x" zu erkennen).

Man schreibt normal ja wohl alle Größen richtig hin.

pluss schrieb:Bei "Meter x Sekunde" erhält man für gewöhnlich die Einheit m/s.

Nein, a ⋅ b = ab und m ⋅ s = ms, eine Geschwindigkeit ist v = m/s also Meter pro Sekunde. Also da scheint doch einiges noch recht seltsam zu sein.

Also generell noch mal, gegeben sind zwei Systeme, S von Bob und S' von Alice, im System S hast Du dann zwei Uhren. System S und S' bewegen sich zueinander mit v = 0.9 c.

Beide Uhren ruhen in S, in S' sind diese dann mit 0.9 c bewegt.

Nun müssen die Größen, also Längen und Zeiten und somit auch Geschwindigkeiten entsprechend von S nach S' richtig transformiert werden, da sollte man dann die LT nehmen.

nocheinPoet schrieb:Nein, a ⋅ b = ab und m ⋅ s = ms, eine Geschwindigkeit v = m/s also Meter pro Sekunde.

Ja, da hast du natürlich recht. Der Fauxpas ist mir unterlaufen weil du vorher mal nach der Geschwindigkeit des Teilchens fragtest und meine Konzentration mehr bei der Arbeit ist. Ist in Bezug auf mein Gedankenexperiment aber ohnehin nicht von Relevanz da der betrachtete Zeitraum eine Periodendauer beträgt und die eben 1 Sekunde.
Also sehe es als korrigiert an, statt m/s natürlich ms.

nocheinPoet schrieb:Also da scheint doch einiges noch recht seltsam zu sein.

Dann immer noch?