Schwierigkeit der Längenkontraktion

nocheinPoet schrieb:Nun gut, ich rechne bei ihm ja nicht mehr mit Verständnis oder Einsicht, aber wenn man sich dann mal dazu im Vergleich einen eigenen Beitrag von @pluss anschaut, ein wenig zurück:

pluss schrieb:
Kann auch die Lösung der weiter vereinfachten Frage aufzeigen:

pluss schrieb:
Ein Körper A bewegt sich im System S mit der Geschwindigkeit u = {ux = 0 , uy = 0,5c}. Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf ux = 0,7 c beschleunigt wurde?

Lösung:

u_x = 0,7c
u_y =0{,}5c

\large |\textcolor{#D0F0E0}{u}| = \sqrt{\textcolor{#D0F0E0}{u_x}^{2} + \textcolor{#D0F0E0}{u_y}^{2}} = \sqrt{ (\textcolor{#D0F0E0}{0,5\:c})^{2} + (\textcolor{#D0F0E0}{0,7\:c})^{2}} = \textcolor{#D0F0E0}{0,86\:c}

verwundert seine Antwort dann doch.


Also @pluss nimmt gleiche Werte wie ich, gleiche Bezeichner, gleiche Rechnung, gleiche Formel und kommt zum gleichen Ergebnis wie ich.

Ach, plötzlich vertrittst du auch meine Ansicht?

Ist ja schön das du deinen Irrtum endlich mal eingestanden hast, jetzt musst du nur noch @mojorisin davon überzeugen das da eben \mathbf u \lbrace 0{,}7,0{,}5,0 \rbrace = 0{,}86c und nicht \mathbf u \lbrace 0{,}7,0{,}357,0 \rbrace =0{,}786c bei rauskommt. Viel Spaß dabei.

@pluss

pluss schrieb:Ach, plötzlich vertrittst du auch meine Ansicht?

Du bist ein Trickser und Lügner, Du hast doch auf meine Antwort mit eben genau dieser Gleichung mit dem Pythagoras geschrieben:

pluss schrieb am 10.03.2018:Du meinst den Bullshit hier: [hier die Gleichung von mir] Bullshit deshalb, weil du so auf Überlichtgeschwindigkeit kommst wenn z.B. \parallel u_x=0,75 + \bot u_y = 0,75c addiert werden sollen.

Wenn Pythagoras, dann den relativistischen bitte. Also, ich Frage dich nochmals: ...

So, das hast Du am 10.03.2018 geschrieben, also vor 16 Tagen. Da warst Du also noch ganz klar anderer Meinung als ich, da hast Du meine Rechnung als Bullshit abgewertet und bezeichnet.

---

Und sogar noch in einem Beitrag darunter dann den "relativistischen" Pythagoras "gezeigt", der genommen werden sollen müsste:

pluss schrieb am 10.03.2018:Kleine Nachhilfe in der SRT für dich @nocheinPoet, der sieht so aus:

\large w=v \perp u=\sqrt{u_y^2+ \left (\frac {dx} {dt} \right )^2 - \frac {u_y^2 \left ( \frac {dx} {dt} \right )^2} {c^2} }

Also wenn, dann vertrittst Du nun auf einmal wohl meine Ansicht und ich nicht Deine. Denn bis hier kam ja nichts in dieser Richtung von Dir, Du wolltest eben diese Rechnung von mir die ganze letzte Zeit nicht anerkennen, hast ja Bullshit dazu gesagt.

---

pluss schrieb:Ist ja schön das du deinen Irrtum endlich mal eingestanden hast, ...

Du, ich habe wie eben belegt und aufzeigt keinen Irrtum eingestanden. Ich erkläre Dir schon recht lange, dass Geschwindigkeiten welche in nur einem System gegeben werden eben so addiert werden, wenn sie rechtwinklig zueinander stehen. Hat man Geschwindigkeiten in nur einem System braucht man keine Lorentztransformation. Auch @mojorisin hat das Dir immer wieder erklärt. Im Team erklären wir es Dir schon einige Monate.

Kann man davon nun ausgehen, dass Du hier nun Deinen Irrtum eingestehst, auch wenn Du es versuchst zu verdrehen und als meinen zu verkaufen?

Kann ich ja kaum glauben ... :D

---

pluss schrieb:... jetzt musst du nur noch @mojorisin davon überzeugen das da eben \mathbf u \lbrace 0{,}7,0{,}5,0 \rbrace = 0{,}86c und nicht \mathbf u \lbrace 0{,}7,0{,}357,0 \rbrace =0{,}786c bei rauskommt. Viel Spaß dabei.

Und wieder versuchst Du hier andere über den Tisch zu ziehen, nun meinst Du Du kommst aus der Nummer raus, wenn Du die Werte einfach so in Klammern schreibst und gar nicht mehr das System dazu nennst. Ich muss da @mojorisin nicht von überzeugen so geschrieben sind es eben immer zwei Geschwindigkeitswerte in nur einem System. Ganz sicher hat also @mojorisin an keiner Stelle hier im Thread auch nur einmal etwas anderes behauptet. Ganz deutlich, wenn Du das hier im System S von Alice misst:

\mathbf \textcolor{#D0F0E0}{u}\: \lbrace \textcolor{#D0F0E0}{0,7\:c}\:|\:\textcolor{#D0F0E0}{0,5\:c} \rbrace = \textcolor{#D0F0E0}{0,86\:c}


sind es die zwei Geschwindigkeiten in ihrem System:

\textcolor{#D0F0E0}{u_x} = \textcolor{#D0F0E0}{0,7\:c}
\textcolor{#D0F0E0}{u_y} = \textcolor{#D0F0E0}{0,5\:c}

zusammen eben |u| = \textcolor{#D0F0E0}{0,86\:c}


Und etwas anders ist es mit:

\mathbf \textcolor{#D0F0E0}{u}\: \lbrace \textcolor{#D0F0E0}{0,7\:c}\:|\:\textcolor{#D0E0F0}{0,357\:c} \rbrace = \textcolor{#D0F0E0}{0,786\:c}


Denn da ist die Geschwindigkeit auf der y-Achse kleiner in ihrem System:

\textcolor{#D0F0E0}{u_x} = \textcolor{#D0F0E0}{0,700\:c}
\textcolor{#D0F0E0}{u_y} = \textcolor{#D0F0E0}{0,357\:c}

zusammen eben |u| = \textcolor{#D0F0E0}{0,786\:c}

---

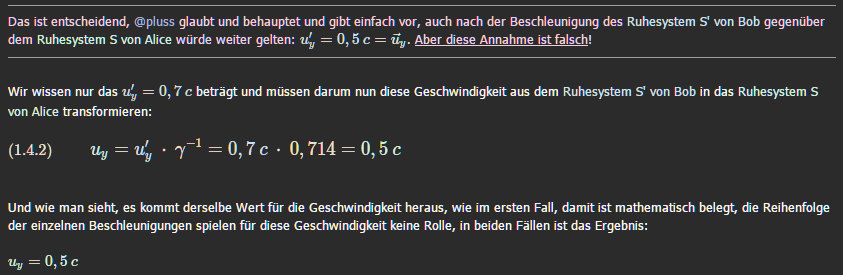
Siehst Du, ich wusste doch, etwas über ein halbes Jahr reichen Dir einfach nicht um diese Dinge richtig zu begreifen. :D Noch immer verstehst Du den Weg aus dem System S' von Bob in das System S von Alice nicht. Schau, Bob misst in S':

\textcolor{#D0E0F0}{u'_x} = \textcolor{#D0E0F0}{0,0\:c}
\textcolor{#D0E0F0}{u'_y} = \textcolor{#D0E0F0}{0,5\:c}


Und nun wird eben die Geschwindigkeit auf der y-Achse \textcolor{#D0F0E0}{u'_y} = \textcolor{#D0F0E0}{0,5\:c} aus dem System S' von Bob mit der Lorentztransformation in das System S von Alice transformiert:

\textcolor{#D0F0E0}{u_y} = \textcolor{#D0E0F0}{u'_y} \cdot \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \textcolor{#D0E0F0}{u'_y} \cdot \gamma^{\:-1} = \textcolor{#D0E0F0}{0,5\:c} \cdot 1,4^{\:-1} = \textcolor{#D0F0E0}{0,357\:c}


So mal am Rande, genau diese Transformation findest Du auch in Deinem Buch auf Seite 207. Genau mit der Gleichung von dort bekommst Du hier auch dieses Ergebnis, Du musst natürlich die Werte richtig in die Gleichung einsetzten:

\textcolor{#D0F0E0}{u_y} = \textcolor{#D0E0F0}{u'_y} \cdot \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \textcolor{#D0E0F0}{u'_y} \cdot \gamma^{\:-1} = \textcolor{#D0E0F0}{0,5\:c} \cdot 1,4^{\:-1} = \textcolor{#D0F0E0}{0,357\:c}


Nein das ist kein Fehler, ich habe auch beim ersten Mal schon die Gleichung von @pluss aus dem Buch von Seite 207 genommen. Aber eventuell hilft es ja, wenn er es zwei mal nach einander so lesen kann, ganz sicher kann es ihm nicht mehr schaden, also wenn man es richtig rechnet hat man dann eben die beiden Geschwindigkeiten im System S von Alice:

\textcolor{#D0F0E0}{u_x} = \textcolor{#D0F0E0}{0,700\:c}
\textcolor{#D0F0E0}{u_y} = \textcolor{#D0F0E0}{0,357\:c}

---

Du machst eben noch immer den gleichen alten Fehler, Du willst eben \textcolor{#D0E0F0}{u_y} = \textcolor{#D0F0E0}{u'_y} = \textcolor{#F0E0D0}{0,5\:c} setzen. Du willst die \textcolor{#D0E0F0}{u'_y} =\textcolor{#D0E0F0}{0,5\:c} aus dem System S' von Bob in das System S von Alice ohne Lorentztransformation übernehmen und dort dann \textcolor{#D0F0E0}{u_y} =\textcolor{#D0F0E0}{0,5\:c} "messen".

Das ist aber einfach falsch, die Geschwindigkeit welche Bob in seinem System S' auf der y-Achse misst, muss mit der Lorentztransformation in das System S von Alice transformiert werden. Eben weil das System S' von Bob sich gegenüber dem System von Alice bewegt. Und das zeigt auch die Gleichung in dem Buch auf Seite 207. Da werden aus den \textcolor{#D0F0E0}{u_y'} = \textcolor{#D0F0E0}{0,6\:c} , welche der mit (auf der x-Achse) bewegte Beobachter misst, nun \textcolor{#D0E0F0}{u_y} = \textcolor{#D0E0F0}{0,48\:c} .


Zu den alten Werten davor zurück, Du kannst es auch so schreiben:

\mathbf \textcolor{#D0E0F0}{u}\: \lbrace \textcolor{#D0E0F0}{u_x}\:|\:\textcolor{#D0F0E0}{u'_y} \cdot \gamma^{\:-1} \rbrace = \lbrace \textcolor{#D0E0F0}{0,7\:c}\:|\:\textcolor{#D0F0E0}{0,5\:c} \cdot 1,4^{\:-1} \rbrace = \lbrace \textcolor{#D0E0F0}{0,7\:c}\:|\:\textcolor{#D0E0F0}{0,357\:c} \rbrace = \textcolor{#D0E0F0}{0,786\:c}


Oder im System S' von Bob:

\mathbf \textcolor{#D0F0E0}{u'}\: \lbrace \textcolor{#D0F0E0}{u_x'}\: | \: \textcolor{#D0E0F0}{u_y} \cdot \gamma \rbrace = \lbrace \textcolor{#D0F0E0}{0,0\:c}\: | \:\textcolor{#D0E0F0}{0,357\:c} \cdot 1,4 \rbrace = \lbrace \textcolor{#D0F0E0}{0,0\:c}\: | \:\textcolor{#D0F0E0}{0,5\:c} \rbrace = \textcolor{#D0F0E0}{0,5\:c}

Also @pluss dann mal schön weiter üben, klar, schon schwer so mit zwei Systemen, aber Du hast doch auch Schleifchen binden geschafft, oder nicht?

... ;)

So, eben mal versehentlich da an einigen Stellen die Farben vertauscht, also alle Werte im System S' von Bob sollen bläulich sein und die in S von Alice grünlich. Kann ja mal vorkommen ...

nocheinPoet schrieb:So, das hast Du am 10.03.2018 geschrieben, also vor 16 Tagen. Da warst Du also noch ganz klar anderer Meinung als ich, da hast Du meine Rechnung als Bullshit abgewertet und bezeichnet.

Bin da auch immer noch anderer Meinung. Auch bleibt deine dortige Antwort Bullshit, nur schnallst du nicht das sich deine Antwort dort auf folgende Frage bezog:

mojorisin schrieb am 11.02.2018:Also nurn noch das unbeschleunigte S. Wir haben die Kugel 2 die bewegt sichmit uy = 0,5c. Von links kommt Kugel 1 mit 0,7c. Nun stoßen sich beide so das Kugel 1 den gesamt IMpuls an Kugel 2 abgibt, aölso stehen bleibt und der gesamte IMpuls in Kugel 2 steckt.

Klar sollte sein der Gesamtimpuls vor dem Stoß sollte gleich sein wie der IMpuls nach dem Stoß .

Wie groß sind ux und uy nbach dem Stoß?

und eben nicht auf diese

pluss schrieb am 07.02.2018:Ein Körper A bewegt sich im System S mit der Geschwindigkeit \mathbf u= \lbrace u_x=0, u_y=0{,}5c \rbrace
Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf u_x=0{,}7c beschleunigt wurde?

Die Frage entspricht meinem GE wenn nach der Beschleunigung der Kugel auf 0,5c der y-Achse, die Rakete und somit auch die Kugel, auf 0,7c aus Sicht von Alice auf der x-Achse beschleunigt wird.

Und da kommst du ja nun, wie ich, auch auf \mathbf u \lbrace 0{,}7,0{,}5,0 \rbrace =0{,}86c und nicht wie @mojorisin auf \mathbf u \lbrace 0{,}7,0{,}357,0 \rbrace =0{,}786c.

@pluss

pluss schrieb:Bin da auch immer noch anderer Meinung. Auch bleibt deine dortige Antwort Bullshit, nur schnallst du nicht das sich deine Antwort dort auf folgende Frage bezog:

mojorisin schrieb am 11.02.2018:Also nun noch das unbeschleunigte S. Wir haben die Kugel 2 die bewegt sich mit u_y = 0,5 c. Von links kommt Kugel 1 mit 0,7 c. Nun stoßen sich beide so das Kugel 1 den gesamt Impuls an Kugel 2 abgibt, also stehen bleibt und der gesamte Impuls in Kugel 2 steckt. Klar sollte sein der Gesamtimpuls vor dem Stoß sollte gleich sein wie der Impuls nach dem Stoß. Wie groß sind u_x und uy nach dem Stoß?

Klar bist Du anderer Meinung, @mojorisin und ich sind eben derselben Meinung wie es die SRT beschreibt, sind uns auch beide einig. Du siehst es anders als wir und stehst damit eben im Widerspruch zur SRT.

Was war denn mit dem Läufer auf dem Zug?

Da hast Du u_x = 0,9 c behauptet, wir haben die beide belegt, Du irrst, es sind eben 0,3923 c. Und das sogar nach Deiner eigenen Rechnung. Habe es Dir ein paar mal erklärt, verlinkt, auch Deine Rechnung dazu, aber Du ignorierst es eben. Denkst wohl, eine Weile warten und dann ist es vergessen. :D

Nein @pluss so geht es nicht, Du hast Unfug behauptet, falsches, stehst sogar zu Deinen eigenen Aussagen im Widerspruch.

---

pluss schrieb:... und eben nicht auf diese:

pluss schrieb am 07.02.2018:Ein Körper A bewegt sich im System S mit der Geschwindigkeit \mathbf \textcolor{#D0E0F0}{u}\: \lbrace \textcolor{#D0E0F0}{0,0\:c}\:|\:\textcolor{#D0E0F0}{0,5\:c} \rbrace. Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf \textcolor{#D0E0F0}{u_x} = \textcolor{#D0E0F0}{0,7\:c} beschleunigt wurde?

Die Frage entspricht meinem GE wenn nach der Beschleunigung der Kugel auf 0,5c der y-Achse, die Rakete und somit auch die Kugel, auf 0,7c aus Sicht von Alice auf der x-Achse beschleunigt wird. Und da kommst du ja nun, wie ich, auch auf \mathbf \textcolor{#D0E0F0}{u}\: \lbrace \textcolor{#D0E0F0}{0,7\:c}\:|\:\textcolor{#D0E0F0}{0,5\:c} \rbrace = \textcolor{#D0E0F0}{0,86\:c} und nicht wie @mojorisin auf \mathbf \textcolor{#D0E0F0}{u}\: \lbrace \textcolor{#D0E0F0}{0,7\:c}\:|\:\textcolor{#D0E0F0}{0,357\:c} \rbrace = \textcolor{#D0E0F0}{0,786\:c}.

Nein das ist nicht richtig. Du versucht mal wieder die Dinge zu verdrehen, ich komme immer auf gleiche Werte wie @mojorisin, da diese sich auch aus der SRT eben so ergeben.

Noch ein weiteres mal, mal wieder, gibst Du in S erst \textcolor{#D0F0E0}{u_y} = \textcolor{#D0F0E0}{0,5\:c} vor und beschleunigst dann das System S' mit der Kugel und Bob auf \textcolor{#D0E0F0}{u_x} = \textcolor{#D0E0F0}{0,7\:c} wirst Du da bei Bob in S' weiter \textcolor{#D0E0F0}{u_y'} = \textcolor{#D0E0F0}{0,5\:c} messen. Aber die Geschwindigkeit auf der y-Achse im System S beträgt dann nur noch \textcolor{#D0F0E0}{u_y} = \textcolor{#D0F0E0}{0,357\:c} .

---

Ich weiß, Dir passt das so nicht und darum versuchst Du die ganze Zeit eben das System S' von Bob zu unterschlagen. :D

Hilft aber nichts, es existiert ja dennoch. Das ist eben das System in dem der Beobachter, hier eben Bob, sich zur Kugel nicht auf der x-Achse bewegt. Und in diesem System werden eben weiter die \textcolor{#D0E0F0}{u_y'} = \textcolor{#D0E0F0}{0,5\:c} gemessen.

So, nun versuchst Du einfach die \textcolor{#D0E0F0}{u_y} = \textcolor{#D0E0F0}{0,5\:c} in S festzunageln. Kann man machen, dann misst man aber im System S' \textcolor{#D0F0E0}{u'_y} = \textcolor{#D0F0E0}{0,7\:c}

---

Weil Du es so nicht begreifen willst, wurde Dir ja schon vorgeschlagen, nicht S' zu beschleunigen, sondern S, auf Grund des Relativitätsprinzips schon klassisch nach Newton kein Problem. Die Szenerie ist physikalisch am Ende gleich.

Aber da stinkst Du dann frech gegen das klassische Relativitätsprinzips an, denn das muss dann einfach falsch sein, weil sonst eben Du ja falsch liegen würdest. :D

Es bleibt wie es ist, Du musst die Geschwindigkeiten und deren Bezeichner einfach klar und richtig in den entsprechenden Systemen vorgeben und dann passt das auch alles. Aber genau das versuchst Du zu vermeiden, Du willst hier verschleiern, nicht die Dinge klären.

Und da Du das so gezielt machst ist einfach lange klar, Du weißt Du liegst falsch.

nocheinPoet schrieb:Du bist ein Trickser und Lügner

Weil du durch deine eigenen Textwände nicht mehr durchsteigst, sollen andere Trickser und Lügner sein?
Dein Problem besteht darin, dass du selbst einfachste Textaufgaben entweder nicht vollumfänglich erfassen kannst, oder dir die grundlegenden Kenntnisse der SRT zur korrekten Lösung fehlen.

pluss schrieb am 10.02.2018:Ich stelle dir mal eine einfache Frage:

Frage an die Natur:
Ein Körper A bewegt sich im System S mit der Geschwindigkeit u= \lbrace u_x=0,u_y=0{,}5c \rbrace
Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf u_x=0{,}7c beschleunigt wurde?

Lässt sich diese Aufgabe deiner Ansicht nach ohne weitere Annahmen lösen?

Darauf antwortete @mojorisin wie folgt:

mojorisin schrieb am 10.02.2018:Ja, ist ja genau unser GE. Ich habe ja die Lösungen in der Tabelle gepostet, daher bin ich am Rätseln warum du überhaupt so eine Frage stellst.

Aus seiner Tabelle (siehe Spoiler) folgt: u_x=0{,}7c und u_y=0{,}357c

Die selbe Frage hast du @nocheinPoet wie folgt beantwortet:

nocheinPoet schrieb:Lösung:

u_x = 0,7c
u_y =0,5c

\large |\textcolor{#D0F0E0}{u}| = \sqrt{\textcolor{#D0F0E0}{u_x}^{2} + \textcolor{#D0F0E0}{u_y}^{2}} = \sqrt{ (\textcolor{#D0F0E0}{0,5\:c})^{2} + (\textcolor{#D0F0E0}{0,7\:c})^{2}} = \textcolor{#D0F0E0}{0,86\:c}

Damit ist deine Aussage

nocheinPoet schrieb: @mojorisin und ich sind eben derselben Meinung wie es die SRT beschreibt, sind uns auch beide einig.

eindeutig wiederlegt.

Nochmals in groß für dich zum mitschreiben:

@mojorisin behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}357c aufweist.

@nocheinPoet behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}5c aufweist.

Spoiler

@pluss

pluss schrieb:Weil du durch deine eigenen Textwände nicht mehr durchsteigst, sollen andere Trickser und Lügner sein? Dein Problem besteht darin, dass du selbst einfachste Textaufgaben entweder nicht vollumfänglich erfassen kannst, oder dir die grundlegenden Kenntnisse der SRT zur korrekten Lösung fehlen. Ich stelle dir mal eine einfache Frage:

pluss schrieb am 10.02.2018:Frage an die Natur: Ein Körper A bewegt sich im System S mit der Geschwindigkeit u= \lbrace u_x=0,u_y=0{,}5c \rbrace Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf u_x=0{,}7c beschleunigt wurde? Lässt sich diese Aufgabe deiner Ansicht nach ohne weitere Annahmen lösen?

Die selbe Frage hast du @nocheinPoet wie folgt beantwortet:

nocheinPoet schrieb:
\large |\textcolor{#D0F0E0}{u}| = \sqrt{\textcolor{#D0F0E0}{u_x}^{2} + \textcolor{#D0F0E0}{u_y}^{2}} = \sqrt{ (\textcolor{#D0F0E0}{0,5\:c})^{2} + (\textcolor{#D0F0E0}{0,7\:c})^{2}} = \textcolor{#D0F0E0}{0,86\:c}

Unglaublich, das ist mal wieder so kack frech gelogen, vor allem wenn man dann mal dem Link eben von Dir zu meinem Beitrag folgt und es dann dort nachliest. Ich habe sogar noch extra die Frage von Dir zitiert, auf die ich antworte:

nocheinPoet schrieb:Vor kurzen fragte mich @pluss nach einer Rechnung:

pluss schrieb am 10.03.2018:Die Frage war "wie werden ebene zu senkrechten und senkrechte zu ebenen Geschwindigkeiten relativistisch korrekt addiert".

Jetzt begriffen?

Das war die Frage, die Frage die ich da in dem Beitrag beantworte und nicht eine andere Frage, Du versuchst nun meine Antwort einfach richtig verlogen an eine ganz andere Frage zu knüpfen. Behauptest frech, meine Antwort wäre ja für diese Frage ... gewesen.

Nein, jeder wird das hier wohl erkennen, Du lügst. Und da Du selber noch den Beitrag von mir verlinkt hast, wo ich eben genau die Frage, welche ich beantworte noch mal extra zitiert habe, kann man kaum glauben, dass Du das nicht verstanden hast. Man muss davon ausgehen, Du machst das gezielt.

---

Und meine Antwort, auf die eben zitierte Frage war auch mehr als nur die Gleichung, auch das unterschlägst Du, eben weil auch daraus klar zu erkennen ist, dass ich eben auf die andere Frage antworte:

nocheinPoet schrieb am 25.02.2018:Hat man nur ein System, braucht man keine SRT, keine Transformation und somit gibt es da auch kein "relativistische" Addition von irgendwelchen Geschwindigkeiten. Die Addition ist einfach ganz normale Vektorrechnung, und wenn da zwei Geschwindigkeitsvektoren in einem rechten Winkel in einem System zueinander stehen, dann geht das über den Pytaghoras und das machst Du ja auch selber schon. Dennoch mal ein aktuelles Beispiel:

\large |\textcolor{#D0F0E0}{u}| = \sqrt{\textcolor{#D0F0E0}{u_x}^{2} + \textcolor{#D0F0E0}{u_y}^{2}} = \sqrt{ (\textcolor{#D0F0E0}{0,5\:c})^{2} + (\textcolor{#D0F0E0}{0,7\:c})^{2}} = \textcolor{#D0F0E0}{0,86\:c}

So und das war eben die Antwort auf die Frage von Dir:

pluss schrieb am 10.03.2018:Die Frage war "wie werden ebene zu senkrechten und senkrechte zu ebenen Geschwindigkeiten relativistisch korrekt addiert".

Und keine andere!

Also natürlich trickst und lügst Du wieder. Oder soll man echt glauben, Du hast den anderen Beitrag von mir echt nicht verstanden, echt nicht begriffen, dass ich die Frage beantworte, welche ich da extra noch mal vorab zitiert habe?

---

pluss schrieb:Nochmals in groß für dich zum mitschreiben:

@nocheinPoet behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}5c =0,357c aufweist.

Nein behaupte ich nicht, Du lügst, Du unterstellst mir was, Du nimmst eine Antwort von mir und versuchst diese mit einer falschen Frage zu verknüpfen. Und dann schreibst Du hier einfach "nocheinPoet würde behaupten, dass ..." was ich so nie behauptet habe. Meine Aussage zur Gleichung unterschlägst Du eben auch extra deswegen, weil sonst eben klar erkennbar ist, was ich behauptet habe.

Ich sage die ganze Zeit, wenn Bob in S' u'_y = 0,5 c misst, dann misst Alice in S eben u_y = 0,357 c. Und zwar wenn sich S und S mit v_x = 0,7 c zueinander bewegen.

Und die |u| = 0,86 c gibt es in S nur, wenn dort schon u_y = 0,5 c vorgegeben ist.

Aber das weißt Du ja alles, muss schon wo hart sein, wenn man da wie Du nicht mehr zurück kann und nun auf so billige Tricks und Lügen zurückgreifen muss. :D

pluss schrieb:@nocheinPoet behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}5c aufweist.

nocheinPoet schrieb:Nein behaupte ich nicht, Du lügst, Du unterstellst mir was

Nein, wie geschrieben, du blickst durch deine eigenen Textwände nicht mehr durch.
Hier nochmals die Frage und deine Lösung (extra rot umrandet damit du weißt was du geschrieben hast:


Quelle: Beitrag von nocheinPoet (Seite 107)

Wenn dir das nicht reicht, hier ein weiterer Beleg das meine Aussage absolut korrekt ist:

nocheinPoet schrieb am 05.03.2018:Und wie man sieht, es kommt derselbe Wert für die Geschwindigkeit heraus, wie im ersten Fall, damit ist mathematisch belegt, die Reihenfolge der einzelnen Beschleunigungen spielen für diese Geschwindigkeit keine Rolle, in beiden Fällen ist das Ergebnis:

\textcolor{#D0F0E0}{{u_y}} = \textcolor{#D0F0E0}{0,5\:c}

Wenn du selbst schon nicht verstehst was du schreibst, wie willst du denn jemals verstehen was andere schreiben? (Rhetorische Frage, spare dir weitere Textwände)

@pluss

Blind bist Du, das ist Zitat, alles und zwar von Dir, Du hast da Lösung geschrieben. :D

Schaue mal das original Geschriebene "Lösung" von Dir:



Also schaue mal genau hin, ich zitiere Dich wie Du Dich selber zitierst, das "Lösung" ist von Dir und Teil des übergeordneten Zitates. Darum habe ich auch das "Lösung" als Lösung geschrieben. Diese Lösung ist samt dem Text "Lösung" von Dir, auch die Rechnung.


Schauen wir nun mal wie genau ich Dich zitiert habe, Du trickst schon wieder, schneidest frech einfach den ersten Teil weg, wo zum ersten Teil des Zitates steht: "pluss schrieb". Hier nun ganz oben im Bild, es ist ein Doppel-Zitat von Dir:



Hier zum Nachlesen: Beitrag von pluss (Seite 83)

---

pluss schrieb:Wenn dir das nicht reicht, hier ein weiterer Beleg das meine Aussage absolut korrekt ist:

nocheinPoet schrieb am 05.03.2018:Und wie man sieht, es kommt derselbe Wert für die Geschwindigkeit heraus, wie im ersten Fall, damit ist mathematisch belegt, die Reihenfolge der einzelnen Beschleunigungen spielen für diese Geschwindigkeit keine Rolle, in beiden Fällen ist das Ergebnis:

\textcolor{#D0F0E0}{{u_y}} = \textcolor{#D0F0E0}{0,5\:c}

Und wieder beschneidest Du gezielt mein Zitat und unterschlägst den Teil, aus dem hervorgeht, woher das Ergebnis kommt, eben steht das "... und wie man sieht" unter einer Rechnung, eben die Rechnung aus der sich die \textcolor{#D0F0E0}{{u_y}} = \textcolor{#D0F0E0}{0,5\:c} ergeben.


Darum hier nun noch mal mein Zitat als Bild mit de Teil, denn man "sehen" soll:




Und hier noch mal als Zitat als Text, mit der Rechnung dazu:

nocheinPoet schrieb am 05.03.2018:Wir wissen nur das \textcolor{#D0E0F0}{{u'_y}} = \textcolor{#D0E0F0}{0,7\:c} beträgt und müssen darum nun diese Geschwindigkeit aus dem Ruhesystem S' von Bob in das Ruhesystem S von Alice transformieren:

\textcolor{#F0E0D0}{(1.4.2)} \large \qquad \textcolor{#D0F0E0}{{u_y}} = \textcolor{#D0E0F0}{{u'_y}} \: \cdot \: \gamma^{-1} = \textcolor{#D0E0F0}{{0,7\:c}} \: \cdot \: 0,714 = \textcolor{#D0F0E0}{0,5\:c}

Und wie man sieht ...

Auch da ist es wieder eindeutig, die \textcolor{#D0F0E0}{{u_y}} = \textcolor{#D0F0E0}{0,5\:c} ergeben sich weil in diesem Fall die Geschwindigkeit der Kugel im System S' von Bob \textcolor{#D0E0F0}{{u'_y}} = \textcolor{#D0E0F0}{0,7\:c} und nicht \textcolor{#D0E0F0}{{u'_y}} = \textcolor{#D0E0F0}{0,5\:c}. Denn bei \textcolor{#D0E0F0}{{u'_y}} = \textcolor{#D0E0F0}{0,5\:c} misst Alice in ihrem System S dann eben die \textcolor{#D0F0E0}{{u_y}} = \textcolor{#D0F0E0}{0,357\:c}.

---

pluss schrieb:Wenn du selbst schon nicht verstehst was du schreibst, wie willst du denn jemals verstehen was andere schreiben? (Rhetorische Frage, spare dir weitere Textwände)

Du bist wirklich peinlich in Deiner Arroganz, Du machst hier einen Fehler nach dem anderen, unfähig richtig zu lesen, unfähig sogar eigene Beiträge richtig zu erfassen und dann Deine erbärmlichen Versuche hier mir falsche Aussagen unterzuschieben.

Du schneidest Dir hier ganz gezieht Teile aus den Beiträgen von mir und willst damit meine Aussagen in einen anderen Kontext bringen.

Echt schon richtig armselig was Du hier nun inzwischen so in Deiner Fehde abziehst ...

Schon traurig das man hier so dreist lügen darf und das nichtmal sanktioniert wird.

@McMurdo

Traurig ist, dass @pluss selber einfach nicht über den Anstand und das Sozialverhalten verfügt sich zu entschuldigen, im Gegenteil versucht er ja weiter aus Frust hier mich auf jede Art zu diskreditieren, eben auch über Lügen und gezieltes manipulieren meiner Beiträge, wenn er diese dann zitiert.

Und so schweigt er nun wieder einfach ...

Davon abgesehen, er hat selber schon in den Rechnungen zu den beiden Fällen ganz klar gezeigt, dass in keinem Fall die Kugel im System S von Alice gleichschnell auf der y-Achse bewegt ist, wie im System S' von Bob.

In beiden Fällen zeigt er, die Kugel ist im System S' von Bob um den Gammafaktor schneller als im System S von Alice. Und auch umgekehrt, die Kugel bewegt sich im System S von Alice immer um den Gammafaktor langsamer als im System S' von Bob.

Je nach Geschwindigkeit der Kugel in einem System und je nach der Geschwindigkeit beider Systeme untereinander errechnet er ja inzwischen, zumindest hat er es, eben das was wir ihm hier seit über einem halben Jahr erklärt haben.

Damit ist seine Behauptung mit der mechanischen Uhr die nicht dilatiert ja durch seine eigenen Rechnungen schon widerlegt. Nun müsste er nun den Anstand haben mal zuzugeben, sich da eben geirrt zu haben.

Wird aber nicht passieren, jede Wette ...

McMurdo schrieb am 27.03.2018:Schon traurig das man hier so dreist lügen darf und das nichtmal sanktioniert wird.

Difficile est, satiram non scribere.

Wenn du der Ansicht bist dem Kontext hier entnehmen zu können das ich Lüge und das gefälligst sanktioniert gehört, dann klick unten rechts auf den "Melden"-Button.
Vergesse aber nicht deine Behauptung entsprechend zu belegen.

---

nocheinPoet schrieb am 26.03.2018:Du bist ein Trickser und Lügner

Du solltest deine Behauptungen schon belegen.

Wie man das macht zeige ich dir mal auf.
Trickserei belegt man z.B so:

nocheinPoet schrieb am 27.03.2018:pluss schrieb:
Nochmals in groß für dich zum mitschreiben:

@nocheinPoet behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}5c =0,357c aufweist.

Du manipulierst Zitate, denn meine Behauptung, ergänzt mit entsprechenden belegen im Spoiler, lautet so:

pluss schrieb am 27.03.2018:Nochmals in groß für dich zum mitschreiben:

@mojorisin behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}357c aufweist.

@nocheinPoet behauptet das nach der Beschleunigung auf der x-Achse der Geschwindigkeitsvektor auf der y-Achse einen Betrag von u_y=0{,}5c aufweist.

Du hast gezielt das Zitat manipuliert indem du dort einfach u_y=0{,}357c zusätzlich eingefügt hast. Das nennt man "tricksen" und erfüllt auch den Tatbestand der Lüge, denn deine Berechnung die zum gleichen Resultat wie von @mojorisin und mir führte

nocheinPoet schrieb am 24.02.2018:Und darüber hinaus wurde ebenfalls mathematisch belegt, dass die Geschwindigkeit der Kugel im Ruhesystem S von Alice auf der y-Achse \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#E0F0D0}{0,357 c} beträgt, sowie dass die Geschwindigkeit der Kugel im Ruhesystem S' von Bob auf der y-Achse \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#F0D0E0}{0,5 c} beträgt.

hast du selbst als falsch wiederufen:

nocheinPoet schrieb am 05.03.2018:Ich hatte zu dem ersten Fall von @pluss ja hier schon mal was geschrieben, muss aber dazu nochmal anmerken, dass ich da die Geschwindigkeit mit \textcolor{#D0F0E0}{{\vec u_y}} = \textcolor{#D0F0E0}{0,357\:c} berechnet habe, jedoch die Werte und Vorgaben für diese Rechnung nicht zu der Erklärung von @pluss passen. Nimmt man die Werte entsprechend der Vorgabe beträgt die Geschwindigkeit \textcolor{#D0F0E0}{{\vec u_y}} = \textcolor{#D0F0E0}{0,5\:c}, und dieser Wert ergibt sich auch im zweiten Fall, wie ich hier mathematisch belegen werde.

Also erst rechnest du explizit vor das man als Resultat u_y=0{,}357c erhält, gefolgt von einer Textwand, in der du versuchst mein Resultat (obwohl es ebenfalls zu u_y=0{,}357c führt) als falsch darzustellen. Nur wenige Seiten später wiederufst du deinen "mathematischen Beweis" und führst ihn somit ad absurdum, jedoch ohne dein neues Resultat, u_y=0{,}5c, mathematisch zu belegen. Also belege dein neues Resultat mathematisch. Wir befinden uns hier in der Rubrik "Wissenschaft" und nicht "Theologie", wo Behauptungen durch Glauben gerechtfertigt werden können.

Warum du so am tricksen bist dürfte auch klar sein:

pluss schrieb am 24.02.2018:erstaunlicherweise kommt von euch nichts zum Fall 2. Denn wenn ihr versucht Fall 2 zu lösen, werdet ihr erkennen dass bei eurer Vorgehensweise Widersprüche auftauchen und die Impulserhaltung dadurch zwangsweise verletzt wird.

Dir ist bei Präsentation deiner Lösung zu Fall 2 aufgefallen das, wenn du gleichzeitig an deiner Lösung von Fall 1 festhältst, damit meine seid Beginn der Diskussion unveränderte Darstellung bestätigst. Was dir wohl nach wie vor noch nicht klar geworden ist, dein Resultat von Fall 2 entspricht meiner Lösung zu Fall 2. @mojorisin war da etwas schlauer als du, er hat sich zu Fall 2 bis heute nicht geäußert, du hingegen bist mit Vollgas in die Falle gerannt und hast prompt meine vorhersage erfüllt, indem du deine Lösung zu Fall 2 aufgezeigt hast. In Folge dessen hast du deine Lösung zu Fall 1 wiederufen und durch eine Behauptung ersetzt, im glauben somit den Wiederspruch zu entfernen. Damit belegst du nur zwei Dinge

1) Du begreifst nicht, dass deine widerrufene Lösung zu Fall 1 nicht im Widerspruch zu deiner Lösung von Fall 2 stand. Zumindest nicht aus physikalischer Sicht. Sie stand nur im Wiederspruch zu deinen eigenen Behauptungen. Deine "Behauptung" aus Fall 1 folgt u_y=0{,}5c, steht im Übrigen in Widerspruch zu deinem Resultat von Fall 2.

2) Belegst du damit das es dir nicht darum geht hier aufzuzeigen was "physikalisch korrekt ist", sondern nur darum deine vorgefasste Erwartungshaltung irgendwie mathematisch erfüllen und belegen zu können, was dir ja ebenfalls auf ganzer Linie vollkommen misslungen ist. Denn aus deiner ursprünglichen Behauptung, das aus beiden Fällen u_y=0{,}357c folgt, ist zwischenzeitlich u_y=0{,}5c geworden. Was im Übrigen, zumindest in Bezug auf Fall 1 im Wiederspruch zu @mojorisins Ansicht von u_y=0{,}357c steht, und somit deine Behauptung:

nocheinPoet schrieb am 26.03.2018: @mojorisin und ich sind eben derselben Meinung wie es die SRT beschreibt, sind uns auch beide einig.

ebenfalls ad absurdum führt.

mojorisin schrieb am 25.02.2018:Die verlinkte Herleitung für den relativsitischen zweidimensionalen Stoß ist aus einem Grundkurs für Bachelor-Studenten an der Harvard-Universität.

Sie ist nicht allzu komplex aber hast du das benötigte physikalische Rüstzeug um die Herleitung auf eventuelle Fehler zu untersuchen?

Ja, denke über das nötige Rüstzeug zu verfügen.
Wie sieht es mit dir aus, reicht dein nötiges Rüstzeug um deine Behauptungen damit zu belegen?

mojorisin schrieb am 18.03.2018:Der Rest folt im Prinzip der Rechnung im ersten Link ich werde aber noch etwas ausführlicher dazu posten.

Kommt da noch etwas?

mojorisin schrieb am 25.02.2018:Geht deine Lösung auch diesen Weg?

Nein, natürlich nicht. Deine Quelle bezieht sich auf einen zentralen elastischen Stoß von Quantenobjekten.
In Bezug auf dein GE ziehe ich einen nicht zentralen elastischen zweidimensionalen Stoß von Makroobjekten zur Darstellung der physikalischen Vorgänge vor.

pluss schrieb:Wenn du der Ansicht bist dem Kontext hier entnehmen zu können das ich Lüge und das gefälligst sanktioniert gehört, dann klick unten rechts auf den "Melden"-Button.

Ach weisst du ist doch viel lustiger wenn du vor aller Welt hier damit weitermachst.

pluss schrieb:Vergesse aber nicht deine Behauptung entsprechend zu belegen.

Oha, erst hochtrabend mit Latein den Beitrag beginnen und dann so ein fauxpas...

Aber seis drum, ich war in Grammatik auch nie eine 1.
Die Belege hat @nocheinPoet ja schon zusammengestellt. Ist ja alles nachlesbar.

@McMurdo

Ja schon heftig, frag mich ob er sich selber das noch glaubt. Und @mojorisin hat wohl auch keine Lust mehr sich hier von @pluss verarschen zu lassen.

@pluss

pluss schrieb am 02.04.2018:Kommt da noch etwas?

Ja. Kann aber noch dauern, nicht weil es zu schwer ist sondern weil ich aufgrund der hier verlinkten Berechnunge eine Excel-Tabelle machen will die die GEschwindigkeitsvektoren vor und nach dem Stoß anzeigt und zwar so dass man GEschwindigkeitevektoren manuell einstellen kann. Allerdings erst wenn ich wirklich mal Zeit habe, denn da gehen 2 oder 3 Std locker drauf.

Übrigens:

mojorisin schrieb am 23.03.2018:By the way:

mojorisin schrieb:
mojorisin schrieb:
mojorisin schrieb:
Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen. Wie kommt es das die Kugel dann schneller wird? Sollte sie nicht eher langsamer werden?

Bitte nicht ignorieren.

mojorisin schrieb:Ja. Kann aber noch dauern

Moin @mojorisin, kein Problem.

mojorisin schrieb:eine Excel-Tabelle machen will die die GEschwindigkeitsvektoren vor und nach dem Stoß anzeigt und zwar so dass man GEschwindigkeitevektoren manuell einstellen kann.

Das ist eine gute Idee die ich ebenfalls umsetzen werde.

@pluss

pluss schrieb:Das ist eine gute Idee die ich ebenfalls umsetzen werde.

Das ist ja schön aber in der Zwischenzweit beantworte mir doch bitte einfach mal diese Frage:

mojorisin schrieb:mojorisin schrieb:
Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen. Wie kommt es das die Kugel dann schneller wird? Sollte sie nicht eher langsamer werden?

mojorisin schrieb:Das ist ja schön aber in der Zwischenzweit beantworte mir doch bitte einfach mal diese Frage:

Nichts anderes mache ich hier seit annähernd 100 Seiten, so wie du versuchst zu belegen das die Annahme

mojorisin schrieb am 11.04.2018:Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen.

korrekte ist.

mojorisin schrieb am 11.04.2018:eine Excel-Tabelle machen will die die GEschwindigkeitsvektoren vor und nach dem Stoß anzeigt und zwar so dass man GEschwindigkeitevektoren manuell einstellen kann.

Im Anhang befindet sich so eine Excel-Tabelle:



Die grünen Felder müssen ausgefüllt werden, wobei die Beträge (im Rahmen des physikalisch möglichen) frei gewählt werden können. Der Rest sollte selbsterklärend sein.

Nachdem du deine Excel-Tabelle hier eingestellt haben solltest, werde ich eine weitere posten die einen zweidimensionalen zentralen elastischen Stoß auf einer nicht ruhenden Kugel darstellt.

Download Excel-Tabelle(88KB): Nichtzentraler01.xlxs

@pluss

pluss schrieb:Nichts anderes mache ich hier seit annähernd 100 Seiten, so wie du versuchst zu belegen das die Annahme

mojorisin schrieb:
Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen.

korrekte ist.

Die logische Konsequenz deiner Aussage ist, das du davon ausgehst das es physikalische Vorgänge und/oder Objekte gibt die nicht der Zeitdilatation unterliegen.

Konkreter: Wenn Bob gegenüber Alice beschleunigt sieht Alice alle Objekte und Vorgänge in Bobs Raktete zunehmende langsamer ablaufen bis auf die Vertikalgeschwindigkeit der Kugel.