Schwierigkeit der Längenkontraktion

pluss schrieb:Was denn dann?

Eine gute Erklärung oder ein Experiment. Du hast es ja auch verstanden Mittlerweile. :) Ist doch positiv!

McMurdo schrieb:Was ist nun anders wenn ich lediglich die Bezeichnungen vertausche?

Der Unterschied besteht darin das Photonen immer eine Geschwindigkeit von c aufweisen, unabhängig vom Bezugssystem.
Gilt das auch für Körper, die einen Geschwindigkeitsvektor von 0,5c aufweisen?

Oder ist die Geschwindigkeit des Körpers relativ, also abhängig vom Bezugssystem?

pluss schrieb:Der Unterschied besteht darin das Photonen immer eine Geschwindigkeit von c aufweisen, unabhängig vom Bezugssystem.

Genau, Photonenbewegen sich immer mit c. Welchen Unterschied macht es dann für die Photonen wenn ich lediglich die Bezeichnungen der Systeme vertausche?
@pluss

Keinen.
Und wie sieht es für einen Körper mit v=0,5c aus?

pluss schrieb:Keinen

Na siehst du, da hast du es doch.

pluss schrieb:Und wie sieht es für einen Körper mit v=0,5c aus?

Was meinst du? Egal wie schnell der Zug an mir vorbei fährt, der Empfänger empfängt immer noch alle 3 Signale gleichzeitig.

Das mag deine Erwartung sein - kannst du sie mathematisch belegen?

@pluss

So, nun komme ich noch mal zu Deiner Wand der Formeln, ich beginne mal mit der ersten:

pluss schrieb:Beschleunigung der Kugel auf der y-Achse aus Sicht von Alice, nach der Beschleunigung auf der x-Achse:

\large u=v \perp u=\sqrt{u_x^{2}+u_y^{2}-\frac {u_x^{2} \cdot u_y^{2}}{c^{2}}}=\sqrt{0,7c^{2}+0,5c^{2}-\frac {0,7c^{2} \cdot 0,5c^{2}}{1c^{2}}} =0,7858c

Du schreibst dazu: "Beschleunigung der Kugel ..." berechnest aber eine Geschwindigkeit, auch wenn "uns" oder mir bekannt ist, was Du eigentlich meinst, ist das echt mehr als schlecht ausgedrückt. Dann das zu den Quadraten, den Fehler da hat Dir ja schon @mojorisin aufgezeigt. Und Du willst doch den Betrag eines Vektors errechnen, dann kannst Du das auch zeigen.

Und Du gibst zwei Beträge für Geschwindigkeiten vor, eben das was Du mir ja als ganz verwerflich angelastet hat. Dabei auch eine Geschwindigkeit, die es ja gerade zu bestimmten gilt, die Du sogar explizit über einen Impuls bestimmt haben willst. Dann sollte es ja wohl mit einem Impuls beginnen, da wäre auch die Angabe der Masse der Kugel sicher sinnvoll.

---

Aber gut, bleiben wir mal bei der Gesamtgeschwindigkeit |u| der Kugel in S, ich gebe mal was vor, und nicht über u'_y wundern, ich erkläre es noch:

Betrag der Gesamtgeschwindigkeit der Kugel in S:

\vec u_x = 0,7 c
\textcolor{#F0D0E0}{{\vec u'_y}} = \textcolor{#F0D0E0}{0,5 c}

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}} = \sqrt{u_x^{2} + \textcolor{#F0D0E0}{{u'_y}}^{2} - \frac {u_x^{2} \: \cdot \: \textcolor{#F0D0E0}{{u'_y}}^{2}}{c^{2}}} = \sqrt{(0,7 c)^{2} + (\textcolor{#F0D0E0}{{0,5 c}})^{2} - \frac {(0,7 c)^{2} \: \cdot \: (\textcolor{#F0D0E0}{{0,5 c}})^{2}}{c^{2}}} = 0,7858 c

So, nun hat Dir das ja schon auch @mojorisin erklärt, warum da eben u'_y und nicht u_y in der Gleichung stehen muss, damit diese richtig ist. Ich habe dennoch mal u'_y farblich extra hervorgehoben und werde mich auch unabhängig von @mojorisin dazu noch mal äußern und es erklären. Und auch u_y habe ich farblich hervorgehoben.

---

Nun schauen wir uns mal den ersten Teil der Gleichung an und lassen den Teil in der Mitte mal weg:

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}} = 0,7858 c

Sieht doch richtig gut aus, ich weiß, dass auch Du weißt, dass man mit dem Pythagoras zwei Vektoren zusammenaddieren kann, wenn diese rechtwinklig zueinander stehen. Die Gesamtgeschwindigkeit der der Kugel in S ergibt sich also ohne Zweifel und jede Diskussion so:

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}}

---

Jetzt setze ich mal die bekannten Werte für die Variablen ein:

\vec u_x = 0,7 c
\textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#E0F0D0}{0,357 c}

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}} = \sqrt{(0,7c)^{2} + (\textcolor{#E0F0D0}{{0,357c}})^{2}} = 0,7858 c

Passt doch alles und sieht richtig gut aus. Stimmt von den meisten Werten auch mit dem von Dir überein. Damit steht die Geschwindigkeit der Kugel im Ruhesystem S von Alice auf der y-Achse mit \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#E0F0D0}{0,357 c} fest.

---

Und nun schauen wir uns mal Deine (von uns korrigierte) Gleichung an, Du hast da Anstelle von \textcolor{#F0D0E0}{{u'_y}} eben falsch \textcolor{#E0F0D0}{u_y} stehen:

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}} = \sqrt{u_x^{2} + (\textcolor{#F0D0E0}{{u'_y}}^{2} - \frac {u_x^{2} \: \cdot \: \textcolor{#F0D0E0}{{u'_y}}^{2}}{c^{2}}})

Unschwer zu erkennen gibt es da zwei Terme in der Wurzel, ich habe den auf der rechten Seite extra noch mal geklammert. Nun ziehe ich diesen Term auf beiden Seiten raus, die müssen natürlich gleich sein:

\large \textcolor{#E0F0D0}{{u_y}}^{2} = \textcolor{#F0D0E0}{{u'_y}}^{2} - \frac {u_x^{2} \: \cdot \: \textcolor{#F0D0E0}{{u'_y}}^{2}}{c^{2}}

---

Ich ziehe mal auf beiden Seite die Wurzel:

\large \textcolor{#E0F0D0}{{u_y}} = \sqrt{\textcolor{#F0D0E0}{{u'_y}}^{2} - \frac {u_x^{2} \: \cdot \: \textcolor{#F0D0E0}{{u'_y}}^{2}}{c^{2}}}

Auch das sollte klar sein. Nun füge ich mal was hinzu und setze die bekannten Werte ein:

\large \textcolor{#E0F0D0}{{u_y}} = \sqrt{\textcolor{#F0D0E0}{{u'_y}}^{2} - \frac {u_x^{2} \: \cdot \: \textcolor{#F0D0E0}{{u'_y}}^{2}}{c^{2}}} = \textcolor{#F0D0E0}{{u'_y}} \: \cdot \: \gamma^{-1} = \sqrt{(\textcolor{#F0D0E0}{{0,5c}})^{2} - \frac {(0,7c)^{2} \: \cdot \: (\textcolor{#F0D0E0}{{0,5c}})^{2}}{c^{2}}} = \textcolor{#F0D0E0}{{0,5c}} \: \cdot \: \gamma^{-1} = \textcolor{#E0F0D0}{0,357 c}

---

---

Damit ist nun mathematisch belegt, @mojorisin möge widersprechen wenn es nicht so ist, dass die Gleichung von @pluss

\large u=v \perp u=\sqrt{u_x^{2}+u_y^{2}-\frac {u_x^{2} \cdot u_y^{2}}{c^{2}}}=\sqrt{0,7c^{2}+0,5c^{2}-\frac {0,7c^{2} \cdot 0,5c^{2}}{1c^{2}}} =0,7858c

falsch oder fehlerhaft ist. Er hatte ein paar Klammern vergessen, ist nun nicht so tragisch, richtig falsch ist es aber Anstelle von \textcolor{#F0D0E0}{{u'_y}} nun \textcolor{#E0F0D0}{u_y} anzugeben. Die richtig Gleichung lautet:

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}} = \sqrt{u_x^{2} + (\textcolor{#F0D0E0}{{u'_y}}^{2} - \frac {u_x^{2} \: \cdot \: \textcolor{#F0D0E0}{{u'_y}}^{2}}{c^{2}}}) = \sqrt{(0,7 c)^{2} + ((\textcolor{#F0D0E0}{{0,5 c}})^{2} - \frac {(0,7 c)^{2} \: \cdot \: (\textcolor{#F0D0E0}{{0,5 c}})^{2}}{c^{2}})} = 0,7858 c

---

Hier hat @pluss einfach nur \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#F0D0E0}{{0,5c}} \: \cdot \: \gamma^{-1} = \textcolor{#E0F0D0}{0,357 c} umständlich berechnet in seiner Gleichung versteckt gehabt. Es geht natürlich auch einfacher:

\large |u| = \sqrt{u_x^{2} + \textcolor{#E0F0D0}{{u_y}}^{2}} = \sqrt{(0,7c)^{2} + (\textcolor{#F0D0E0}{{0,5c}} \: \cdot \: \gamma^{-1})^{2}}= \sqrt{(0,7c)^{2} + (\textcolor{#E0F0D0}{{0,357c}})^{2}} = 0,7858c

---

Und darüber hinaus wurde ebenfalls mathematisch belegt, dass die Geschwindigkeit der Kugel im Ruhesystem S von Alice auf der y-Achse \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#E0F0D0}{0,357 c} beträgt, sowie dass die Geschwindigkeit der Kugel im Ruhesystem S' von Bob auf der y-Achse \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#F0D0E0}{0,5 c} beträgt.

Schließlich wurde noch mathematisch belegt, dass sich die Geschwindigkeit im Ruhesystem S von Alice auf der y-Achse so:

\large \textcolor{#E0F0D0}{{u_y}} = \textcolor{#F0D0E0}{{u'_y}} \: \cdot \: \gamma^{-1} = \textcolor{#F0D0E0}{{0,5c}} \: \cdot \: \gamma^{-1} = \textcolor{#E0F0D0}{0,357 c}

berechnet.

---

Genau das was ich die ganze Zeit schon viel einfacher vorgerechnet und belegt habe. @pluss hat nachgewiesenermaßen einige Fehler in seiner Gleichung und dazu ist diese auch noch überladen und umständlich.

Nun kann man sich natürlich, warum auch immer, die Geschwindigkeiten nehmen, der Kugel eine Masse von 1 kg zuordnen und die Impulse berechnen, welche dann in den Systemen eben zu diesen Geschwindigkeiten geführt haben. Muss man aber wirklich nicht.

Wie gesagt, auch @pluss gibt ja Werte für die Geschwindigkeiten in den Systemen vor, für die Kugel in S auf der x-Achse eben u_x = 0,7 c. Auch dafür wurde keine Rechnung mit Impuls gezeigt. Und man kann auch die Geschwindigkeit der Kugel im Ruhesystem S' von Bob mit u'_y = 0,5 c vorgeben, hat sogar auch @pluss selber so getan. Er setzt diese ja auch in seiner Gleichung ein, nur bezeichnet er da die 0,5 c eben fälschlich als u_y und nicht richtig als u'_y. Das hat ja auch schon @mojorisin sehr schön aufgezeigt.

Es wird nicht damit gerechnet, dass @pluss den Erklärungen hier folgen kann und noch weniger damit, dass er seinen Fehler einsieht und noch viel weniger damit, dass er dass dann offen hier auch eingesteht.

So, das war nur die erste Gleichung, in den weiteren von @pluss stecken noch "andere Dinge" die man in Ruhe mal genau beleuchten sollte.

@pluss

pluss schrieb:

nocheinPoet schrieb:Und ebenso wurden auch die u'_y = 0,5 c vorgeben.

Ach - von wem denn?

Zuletzt von Dir selber in Deiner ersten Gleichung, nur hast Du es eben falsch als u_y bezeichnet. Wurde Dir ja nun von @mojorisin und auch von mir aufgezeigt, erklärt und mathematisch belegt.

Dann geht es auf @mojorisin und Dich zurück, ich zitiere mal eben:

mojorisin schrieb am 06.02.2018:Ich denke wir sind uns einig das vor der Beschleunigung Ich denke wir sind uns einig das vor der Beschleunigung u'_y = u_y =0,5 c ist.

Und das hast Du selber so bestätigt:

pluss schrieb am 06.02.2018:

mojorisin schrieb am 06.02.2018:Die 0,5 c sind ok?

Ja, sind sie.

Nun wirst Du sicher wieder einwenden, dass es da um den Wert vor der Beschleunigung des Systems S' von Bob gegenüber dem System S von Alice auf der x-Achse geht.

Dein Einwand ist aber nichtig, denn es gilt nun mal noch immer das klassische galileische Relativitätsprinzip. Und daraus folgt eben, dass sich für Bob in seinem Ruhesystem vor und nach einer Beschleunigung nichts ändert, also die Kugel wird eben mit dem System von Bob genommen und kann nicht zur Seite weg. Stecke sie eben in eine Röhre. Ich weiß Du suchst nach jeden Strohalm und wirst wieder versuchen zu tricksen.

Aber eben wegen dem Relativitätsprinzip kann man auch ebenso einfach Bob mit Kugel in "Ruhe" lassen und einfach Alice mit ihrem System S in die andere Richtung auf 0,7 c auf der x-Achse beschleunigen.

Ergibt eben wegen dem Relativitätsprinzip das gleiche Szenario.

Es ist nun eben so @pluss, dass Du ja schon dem Relativitätsprinzip widersprichst, damit der anerkannten Physik über viele 100 Jahre, also noch viel weiter zurück als vor die SRT. Du gehst da sogar vor Newton.

Du kannst nicht verlangen, dass man Dir hier noch diese anerkannten Grundlagen belegt und erklärt. Es ist schon wirklich lächerlich dem Relativitätsprinzip zu widersprechen und dessen Gültigkeit in Abrede zu stellen.

---

So und noch was, Du schreibst:

pluss schrieb:In beiden Fällen hat Bob der Kugel auf der y-Achse einen Impuls von p=0,5773kg⋅c ... übertragen ...

pluss schrieb:Aus dem Impuls folgt eine Geschwindigkeit von: u_y = 0,5 c ...

Also wenn Bob das macht, macht er es in seinem Ruhesystem S' und nicht im Ruhesystem S von Alice. Da macht es dann wirklich schon Sinn, die Geschwindigkeit auch richtig zu benennen eben als u'_y = 0,5 c.

Klar gilt vor der Beschleunigung des Ruhesystems S' von Bob gegenüber dem Ruhesystem S von Alice:

u'_y = u_y = 0,5 c

Aber dennoch ist die richtige Bezeichnung nun mal eben u'_y und nicht u_y.

Und solange es keine Geschwindigkeit zwischen beiden Systemen gibt, ist das doch eh alles uninteressant, ruhen beide Systeme zueinander ist der Lorentzfaktor (LF) eh gleich 1.

Spannend und relevant für die SRT und die Zeitdilatation wird es erst, wenn es eine Geschwindigkeit zwischen beiden Systemen gibt, wie und woher die kommt ist hingegen unwichtig und ändert nichts am Ergebnis.

Beschleunigt Bob seine Kugel in seinem Ruhesystem S' auf der y-Achse auf u'_y = 0,5 c, dann wird in einem anderen zu S' mit 0,7 auf der x-Achse bewegten System S eben die Geschwindigkeit der Kugel auf der y-Achse mit \textcolor{#E0F0D0}{{\vec u_y}} = \textcolor{#F0D0E0}{{0,5c}} \: \cdot \: \gamma^{-1} = \textcolor{#E0F0D0}{0,357 c} gemessen.

Ob Du das nun verstehen kannst oder nicht, ob Du das nun zugeben kannst oder nicht willst, ob Du es nun bestreitest oder nicht, das ergibt sich eben so aus der SRT und die wurde bisher nicht falsifiziert und hat somit Gültigkeit.

Bestreitest Du das stehst Du eben im Widerspruch zur SRT, klingt vielleicht komisch, ist aber so. :D

nocheinPoet schrieb:So, das war nur die erste Gleichung, in den weiteren von @pluss stecken noch "andere Dinge" die man in Ruhe mal genau beleuchten sollte.

Ja, dann mach mal.
Bei Fall 1 bist du auf u_y=0,357c und für u'_y auf 0,5c gekommen.

Auf was für Beträge kommst du denn bei Fall 2?

pluss schrieb:Das mag deine Erwartung sein - kannst du sie mathematisch belegen?

c ist konstant, hast Du selbst geschrieben. Was willst du da noch mathematisch belegen? Das die Lichtgeschwindigkeit immer mit derselben Geschwindigkeit gemessen wird ist in zig Experimenten immer und immer wieder bestätigt worden.
@pluss

Was versteht man überhaupt unter einer Verlängerung?
"Wachsen" die Teilchen, oder nur deren Abstände?

McMurdo schrieb:c ist konstant, hast Du selbst geschrieben.

Was hat das damit zu tun:

pluss schrieb:Und wie sieht es für einen Körper mit v=0,5c aus?

Kannst du mir das näher erklären? Geschwindigkeiten von Körpern sind doch relativ, warum gilt das für die Kugel plötzlich nicht mehr?

Was hat die maximale Geschwindigkeit von 1c für folgen auf das Photon, wenn eine Kraft auf das Photon wirkt?

Angenommen die Lichtuhr ruht zu Dir und weist einen Geschwindigkeitsvektor von u_y=1c auf.
Nun wirkt eine Kraft in Richtung der x-Achse auf das Photon. Was passiert dann mit dem Geschwindigkeitsvektor auf der y-Achse?
Es muss sich, da der resultierende Geschwindigkeitsvektor, also u{u_x, u_y, u_z} immer =1c beträgt, etwas an dem Vektor auf der y-Achse verändern.

Gilt das auch für die Kugel?
Hat die Kugel einen Geschwindigkeitsvektor von u_y=0,5c, ist dieser Vektor dann eine Funktion des Lorentz-Faktors, also einer mathematischen Konstruktion?

Ich unterstütze die Vorstellungskraft mal visuell.
In der Grafik wirkt eine Kraft in Richtung der x-Achse (dicker grüner Pfeil), das Photon wird durch rote Pfeile dargestellt, die Kugel durch grüne. Der rote Teilkreis kennzeichnet die maximale Geschwindigkeit, der grüne Bogen die Funktion des Lorentz-Faktors in Bezug der Geschwindigkeit auf der y-Achse für die Kugel. So sieht es nach Ansicht von dir, mojo und neP aus:



Meiner Ansicht nach müsste es so aussehen, da wie für das Photon, auch für die Kugel gilt: maximale Geschwindigkeit 1c.
Wirkt eine Kraft in Richtung der x-Achse, führt diese zu einer Geschwindigkeitsänderung auf der x-Achse, nicht aber auf einer der anderen Achsen, denn ohne Ursache (wirkende Kraft in y- oder z-Richtung) keine Wirkung (Geschwindigkeitsänderung in y- oder z-Richtung) für die Kugel.

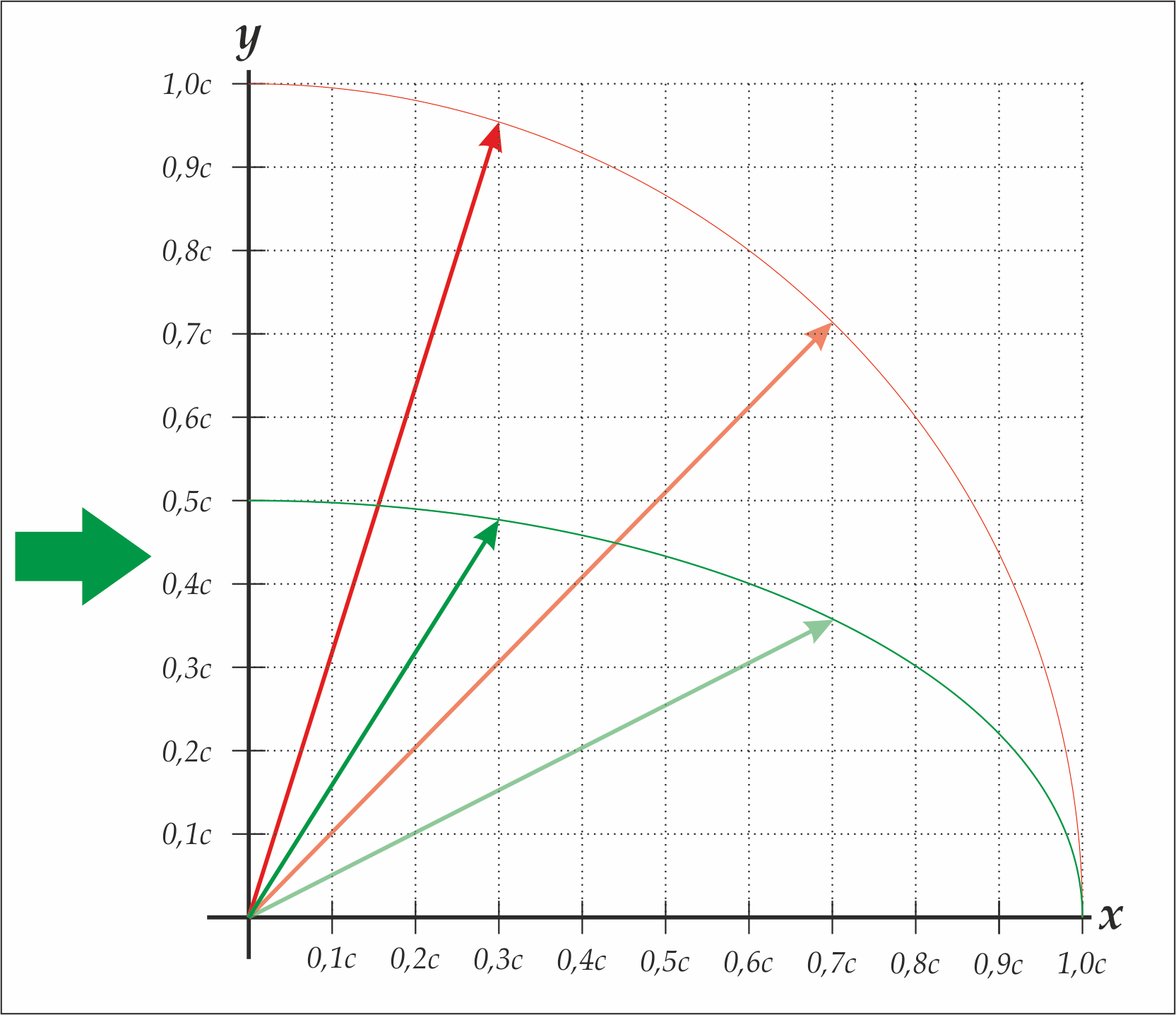
pluss schrieb:Kannst du mir das näher erklären? Geschwindigkeiten von Körpern sind doch relativ, warum gilt das für die Kugel plötzlich nicht mehr?

Für welche Kugel? Die drei Uhren senden exakt immer nach einer Sekunde das Signal und wenn ich 3 Lichtsignale exakt gleichzeitig aussende kommen sie immer exakt gleichzeitig beim Empfänger an. Egal wie schnell sich der Zug oder der Bahnhof bewegen. Auch da hast du zugestimmt.

pluss schrieb:Was hat die maximale Geschwindigkeit von 1c für folgen auf das Photon, wenn eine Kraft auf das Photon wirkt?

Welche Kraft sollte auf das Photon wirken wenn ich da am Bahnhof stehe? Verstehe ich nicht.

pluss schrieb:Angenommen die Lichtuhr ruht zu Dir und weist einen Geschwindigkeitsvektor von uy=1c auf.
Nun wirkt eine Kraft in Richtung der x-Achse auf das Photon.

Auch hier: welche Kraft soll auf das Photon wirken wenn ich mit der Uhr am Bahnhof stehe?

McMurdo schrieb: Auch da hast du zugestimmt.

Nur wenn sich die Uhren auf dem Bahnhof befinden, nicht wenn die Uhren im Zug sind.

McMurdo schrieb:Welche Kraft sollte auf das Photon wirken wenn ich da am Bahnhof stehe? Verstehe ich nicht.

Vielleicht weil du meine Frage vergessen hast?

pluss schrieb:Na dann stelle die 3 Uhren mal in den Zug und den Empfänger auf den Bahnhof. Wie sieht es dann aus?

pluss schrieb:Nur wenn sich die Uhren auf dem Bahnhof befinden, nicht wenn die Uhren im Zug sind.

Das hast selbst zugegen das es egal ist wie dieSysteme bezeichnet sind. Ich kann also Bahnhof mit Zug vertauschen und umgekehrt. Es herrschen beide male dieselben Gesetzmäßigkeiten. Wie sollte das auch anders sein? In dem einen Fall fährt der Zug an mir vorbei, im anderen der Bahnhof. Oder du kannst darlegen welches System gegenüber dem anderen ausgezeichneter ist?

pluss schrieb:Vielleicht weil du meine Frage vergessen hast?

Ich hab sie nicht vergessen aber du hast sie selber schon beantwortet: Es macht keinen Unterschied wie ich die Systeme bezeichne. Auch das hast du schon bestätigt.

McMurdo schrieb:Die drei Uhren senden exakt immer nach einer Sekunde das Signal und wenn ich 3 Lichtsignale exakt gleichzeitig aussende kommen sie immer exakt gleichzeitig beim Empfänger an.

Soweit deine assertorische Aussage, die ohne Beweisführung so sinnvoll in einer Sachdiskussion ist wie ein Abszess am Allerwertesten.

pluss schrieb:Soweit deine assertorische Aussage, die ohne Beweisführung so sinnvoll in einer Sachdiskussion ist wie ein Abszess am Allerwertesten.

Du darfst sie gerne widerlegen.

Beweislastumkehr?
Ne du, belege du mal deine Behauptung. Wenn du das nicht kannst, bin ich nicht der richtige Gesprächspartner für dich.

@pluss

Ich möchte gerne deine Grafiken noch erweiteren und zwar um den Impuls:

Zuerst deine:




Das ganze um den Impuls (Masse = 1 kg) n y-Richtung erweiteret schaut dann so aus:


Wenn u_y konstant und anabhängig wäre würde der y-Impuls mit zunehmender x-Geschwindigkeit ansteigen. Das würde bedeuten es müsste ien Kraft in y-Richtung wirken. Des Weiteren wäre es unmöglich die Kugel in x-Richtung schneller als ~0,82c beschleunigen.


-----------------------------------------------------------------------------------------------------------------------
Nun die andere Grafik:



DAs ganze um den Impuls in y-Richtung erweitert:



Hier ist der Impuls konstant und was bedeutet es benötigt keine Kraft in y-RIchtung. Die Abnahme der Geschwindigkeit der Kugel iny-Richtugn ist ein Effekt der Zeitdilatation, und kein Effekt der einer Kraft bedarf.

Was du bisher nicht verstanden hast: Der Impuls muss immer erhalten bleiben. Das ist wurde bisher in keinem Experiment widerlegt und gilt als physikalisches Grundgesetz. Nach Newton ist der Impuls proportional zur Geschwindigkeit:

während die Masse konstant ist. Das bedeutet eine Änderung der Geschwindigkeit geht einher mit einer Änderung des Impulses. Deine Argumentation:

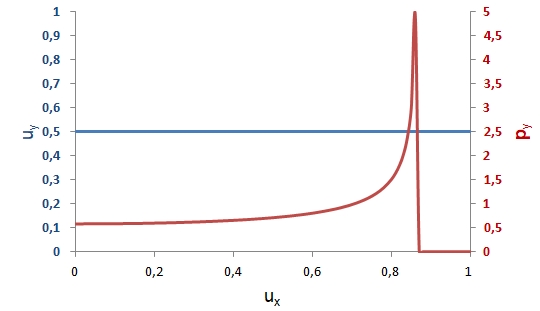
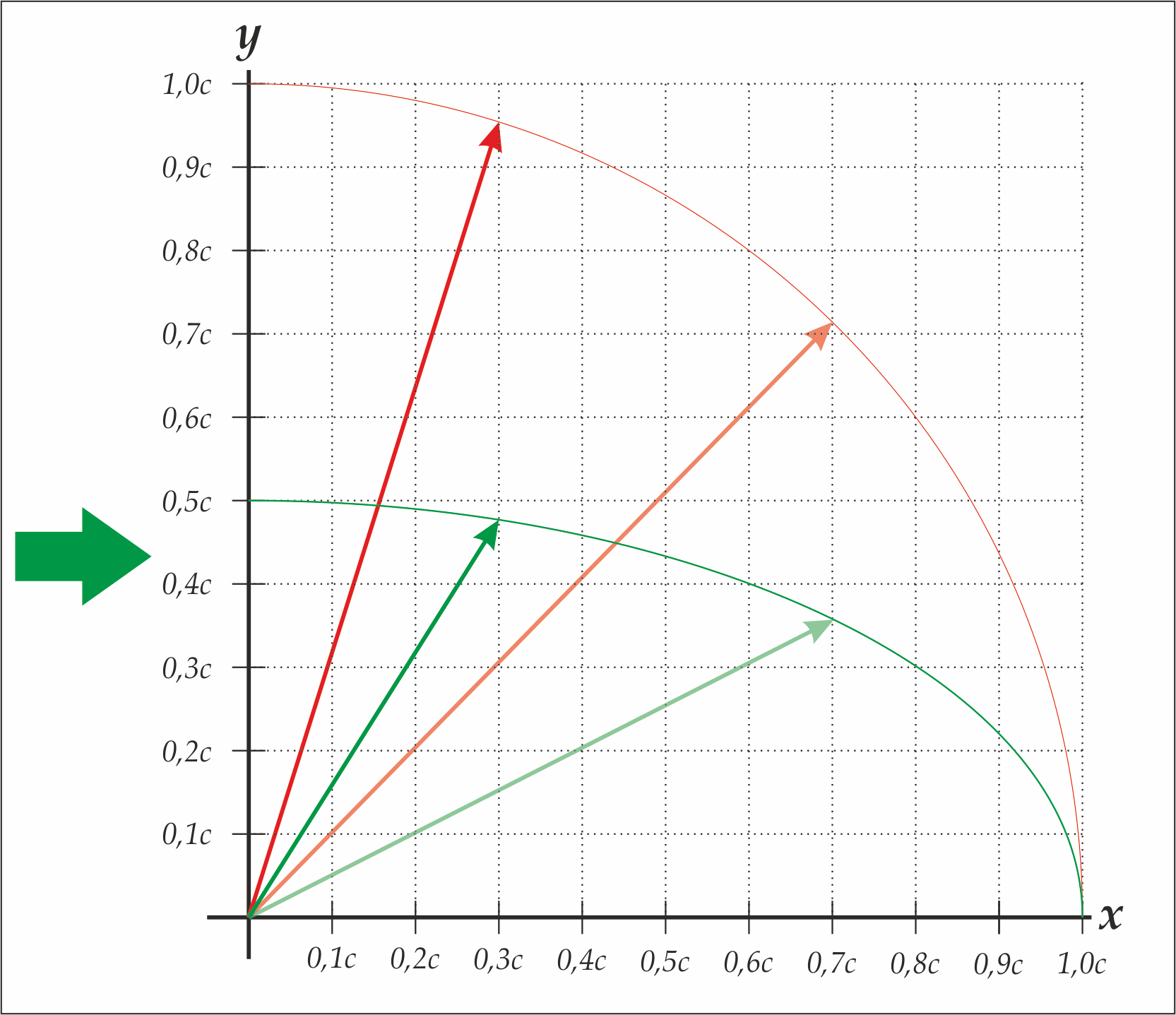
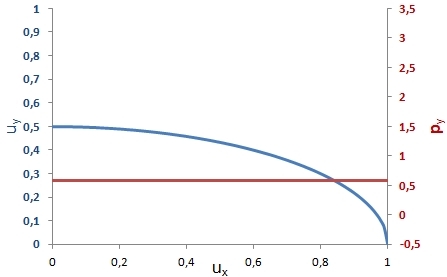
pluss schrieb:Wirkt eine Kraft in Richtung der x-Achse, führt diese zu einer Geschwindigkeitsänderung auf der x-Achse, nicht aber auf einer der anderen Achsen, denn ohne Ursache (wirkende Kraft in y- oder z-Richtung) keine Wirkung (Geschwindigkeitsänderung in y- oder z-Richtung) für die Kugel.

ist richtig. Achtung: Aber nur in der klassischen, newtonschen Physik.

Nicht in der reltivistischen Physik den dort gilt für den Impuls:



Wie man an den Schaubildern sieht ist widerspricht deine Annahme der Impulserhaltung, und verstößt somit gegn die Grundlagen der Physik.

mojorisin schrieb:würde der y-Impuls mit zunehmender x-Geschwindigkeit ansteigen. Das würde bedeuten es müsste ien Kraft in y-Richtung wirken.

Wenn der Geschwindigkeitsvektor auf der x-Achse ansteigt, nimmt auch die Masse zu. Masse ist eine skalare Größe, betrifft folglich auch die y-Achse.

mojorisin schrieb:Des Weiteren wäre es unmöglich die Kugel in x-Richtung schneller als ~0,82c beschleunigen.

Ja, die maximale Geschwindigkeit beträgt 1c. Eine weitere Beschleunigung auf der x-Achse erhöht die Gesamtenergie, führt aber zu keine Steigerung der Geschwindigkeit (Infinitesimale Änderungen mal in den Skat gedrückt). Würde die Kraft, nachdem die resultierende nahezu 1c erreicht hat, auf eine andere Achse wirken, würde nur noch eine Richtungsänderung der resultierenden Geschwindigkeit erfolgen. Was dann natürlich zu den gleichen Veränderungen der Achswerte führt wie bei einem Photon.

mojorisin schrieb:Der Impuls muss immer erhalten bleiben.

Natürlich muss er das. Aber Erhaltung bedeutet nicht, dass der Impuls auf einer Achse konstant bleiben muss.

Das bedeutet Impulserhaltung: \mathbf p=p_1+p_2

Ich hatte dir schon einmal aufgezeigt das du die Impulserhaltung verletzt, nicht ich. Wieso wird das eigentlich immer beharrlich ignoriert?

Ich wiederhole es nochmals und nehme dafür erneut Daten aus deiner Excel-Tabelle, damit du die Richtigkeit überprüfen kannst:

Obere Tabelle System S
1. Impuls: p_y=0{,}57735kg \cdot c (P5 in deiner Tabelle)
2. Impuls: p_x=1{,}131833kg \cdot c (O12 in deiner Tabelle)

Resultierende Geschwindigkeit aus zugeführten Impulsen:
Erster Impuls (p_y):

Zweiter Impuls (p_x):

Daraus resultiert eine Geschwindigkeit \mathbf u \lbrace u_x, u_y \rbrace von (M12 deiner Tabelle):


(Bonus: u_y= \sqrt {\mathbf u^2-u_x^2}= \sqrt {\left (0{,}81927c \right )^2- \left (0{,}7c \right )^2}=0{,}42568. Und was steht bei dir in Feld L12? 0,357c steht da, passt nicht)

Resultierende Geschwindigkeit (M12 deiner Tabelle) aus zugeführtem Gesamtimpuls \mathbf p :


Impulserhaltung verletzt, der resultierende Vektor \mathbf u muss den gleichen Betrag aufweisen.

---

Untere Tabelle System S
1. Impuls: p_y=0{,}57735kg \cdot c (P19 in deiner Tabelle)
2. Impuls: p_x=1{,}372813kg \cdot c (O26 in deiner Tabelle)

Resultierende Geschwindigkeit aus zugeführten Impulsen:

Erster Impuls (p_y):


Zweiter Impuls (p_x):


Daraus resultiert eine Geschwindigkeit \mathbf u \lbrace u_x, u_y \rbrace von (M26 deiner Tabelle):


(Bonus: u_y= \sqrt {\mathbf u^2-u_x^2}= \sqrt {\left (0{,}860233c \right )^2- \left (0{,}7c \right )^2}=0{,}5c. Und was steht bei dir in Feld L26? 0,5c steht da, passt)

Resultierende Geschwindigkeit (M26 deiner Tabelle) aus zugeführtem Gesamtimpuls \mathbf p:


Impulserhaltung nicht verletzt, der resultierende Vektor \mathbf u weist den gleichen Betrag auf.

Das gleiche könnten wir auch mit Fall 1 und Fall 2 durchspielen, aber erstaunlicherweise kommt von euch nichts zum Fall 2. Denn wenn ihr versucht Fall 2 zu lösen, werdet ihr erkennen dass bei eurer Vorgehensweise Widersprüche auftauchen und die Impulserhaltung dadurch zwangsweise verletzt wird.

P.S.:

mojorisin schrieb am 04.02.2018:Das kommt daher das die Geschwindigkeit in dem Maße abnimmt wie die dynamische Masse zunimmt.

Auch da habe ich dir mehrfach nachgewiesen, dass deine Annahme empirisch wiederlegt ist. Zuletzt hier: Beitrag von pluss (Seite 78)

Nehme es bitte mal zur Kenntnis. Solltest du den Widerspruch nicht entkräften können, musst du deine falsifizierte Annahme fallen lassen.