Schwierigkeit der Längenkontraktion

mojorisin schrieb: DAS gilt jedoch nicht für GEschwindigkeiten z.B. der Kugel: Oder willst du behaupten jeder misst die Kugel gleich schnell? WOhl kaum.

Natürlich nicht. Die Beträge spielen keine Rolle in Bezug auf den aufgezeigten Widerspruch:



Nur weil Beträge Lorentz-transformiert werden, egal aus wie vielen Systemen heraus, ändert sich nichts an der Tatsache deiner Behauptung die eben zu diesem Widerspruch führt:

pluss schrieb:Also, erkläre mal warum bei euch ein Impuls mal dazu führt das er vollständig in Geschwindigkeit umgesetzt wird und mal nicht. Ebenfalls bedarf es einer Erklärung warum ein Impuls mal dazu führt, das sich ein senkrecht zum Impuls stehender Geschwindigkeitsvektor verringert und mal nicht.

@pluss

pluss schrieb:Natürlich nicht. Die Beträge spielen keine Rolle in Bezug auf den aufgezeigten Widerspruch:

ALso bevor dashier wieder in endlos Debatten ausartet, werde ich hier mal kurz zusammenfassen:

1. Es geht dir hier um GE 1. Dieses Gedankenexperiment hatten wie hier mal zusammen auf den Punkt gebracht und definiert:

Beitrag von pluss (Seite 78)

pluss schrieb am 06.02.2018:

- In S' ruht die Kugel die ganze Zeit auf der x-Achse.
- In S ruht die Kugel zuerst auf der x-Achse und wird dann beschleunigt
- DIe y-Geschwindigkeit der Kugel vor Beschleunigung betrage in beiden Systemen 0,5c.


uy vor Beschleunigung auf 0,7c
u'y vor Beschleunigung auf 0,7c
uy nach Beschleunigung auf 0,7c
u'y nach Beschleunigung auf 0,7c


Übereinstimmung?

Sehr schön auf den Punkt gebracht. Ja, übereinstimmung zu 100%.

Du bringst nun folgende Grafik um mich in eine Widerspruch zu verwickeln:

Zuerst eine Grafik die zwei Fälle zeigt wobei beide Fälle identisch sind mit 0,7c:



Das meinst du sei widersprüchlich da die "Impulse" bevorzugt werden auf der x-AChse.

Und jetzt kommt deine, deiner Meinung nach, richtige Präsentation:



Hier erreicht die Kugel nach Stoß auf der y-AChse nur noch eine bestimmte x-GEschwindigkeit. Der FAll den du hier präsentierst hast du 1:1 übernommen aus dem Buch. Der WIderspruch den du versuchst mir unterzujubeln kommt allerdings nicht daher das da ein Widerspruch besteht in meinen Resultaten zum GE.

Der kommt daher: Du nimmst die Resultate des GE des Buches und wirfst mir vor das ich nicht auf dieseleben Resultate komme beim unserem GE. Das sind aber zwei unterschiedliche GE.

IN unserem GE geben eine Endgeschwindigkeit auf der x-AChse vor, und du selbst hast gesagt: Übereinstimmung 100%. In unserem GE gibt es auch keine Impulserhaltung auf der x-AChse. Wir sagen einfach die Rakete beschleunigt bis so x,xc und dann betrachten wir die Fälle was mit der Kugel passier vor und nach der Beschleunigung.

Also bevor du mir Widersprüche vorwirfst, dann leite sie auch bitte vom hier Diskutierten ab und nicht von anderen GE.


SpoilerPS: Wir würden dasselbe Resultat wie im Buch erhalten, wen wir folgendes GE machen würden:

Fall 1: Bob beschleunigt auf der x-Achse auf u_x= 0,7c und startet dann die Kugel aus seiner SIcht auf u'_y = 0,5c. WIe schnell wäre die Gesamtgeschwindigkeit u_ges der Kugel aus SIcht von Alice? WIe sind u_x und u_y aus Sicht von ALice?

Antwort:
u_x = 0,7c
u_y = 0,357c
u_ges = 0,786c


Fall 2: Bob beschleunigt auf der y-Achse auf u_y= 0,7c und startet dann die Kugel aus seiner SIcht auf u'_x = 0,5c. WIe schnell wäre die Gesamtgeschwindigkeit u_ges der Kugel aus SIcht von Alice? WIe sind u_x und u_y aus Sicht von ALice?

Antwort:
u_x = 0,357c
u_y = 0,7c
u_ges = 0,786c

@pluss

A propo Widersprüche: DU hast noch nie erklärt warum aus Sicht von Bob, der zu der Kugel auf der x-AChse ruht, die Kugel in die senkrechte y-Richtung schneller wird, obwohl nur eine horizontale Kraft wirkt. Da gab es ja richtige Defizite, da hast du gesagt die Kugel ändert im System S' (also Bob) ihre GEschwindigkeit ohne das sie beschleunigt wird.

mojorisin schrieb:Der kommt daher: Du nimmst die Resultate des GE des Buches und wirfst mir vor das ich nicht auf dieseleben Resultate komme beim unserem GE.

Blödsinn, die Beträge in der Grafik stammen aus deiner Exceltabelle:



Die Beträge hast du selbst berechnet für System S, also Alice:

u_y vor Beschleunigung auf der x-Achse: 0,5c , Feld L5
u_y nach Beschleunigung auf der x-Achse: 0,357c Feld L12
u_x vor Beschleunigung: 0c Feld K5
u_x nach Beschleunigung: 0,7c Feld K12

mojorisin schrieb:A propo Widersprüche: DU hast noch nie erklärt warum aus Sicht von Bob, der zu der Kugel auf der x-AChse ruht, die Kugel in die senkrechte y-Richtung schneller wird, obwohl nur eine horizontale Kraft wirkt.

Doch, sogar mehr als einmal. Wenn sich der Geschwindigkeitsvektor auf der y-Achse aus Sicht von Alice nicht verändert während auf der x-Achse eine Beschleunigung stattfindet, hat die Beschleunigung auf der x-Achse aufgrund v=u_x zur folge das die Zeit in S' langsamer vergeht, was wiederum zur Folge hat das in S' (Strecke/Zeit) der Geschwindigkeitsvektor u'_y ansteigt.

@pluss

pluss schrieb:Blödsinn, die Beträge in der Grafik stammen aus deiner Exceltabelle:

Ja, aber was da berechnet wurde ist nicht dasselbe wie in dem GE in deinem Buch. In unserem GE gab es auf der x-AChse keinen definierten Kraftstoß sondern ein Beschleunigung bis u_x einen gegebenen Wert erreicht.

Daher gibt es zwischen dem GE und unserem GE ein gravieren Unterschied hinsichtlich der Beschleunigung:

Unser GE	Impuls offen	Geschwindigkeit vorgegeben
Dein Buch	Impuls vorgegebn	Geschwindigkeit offen

en

In der Tabelle die ich gepostet habe sind die Zwischenwerte von 0 bis 0,7c auch geplottet, da wir ja auch noch Beschleunigung mittendrin hatten. @pluss ehrlich es ist so anstrengend. Du stimmst darauf ein das wir Äpfel betrachten und nachher kommst du daher und sagst meine Birnen sehen nicht wie Birnen aus, weil ich habe da ja nur Äpfel.

pluss schrieb: hat die Beschleunigung auf der x-Achse aufgrund v=ux zur folge das die Zeit in S' langsamer vergeht, was wiederum zur Folge hat das in S' (Strecke/Zeit) der Geschwindigkeitsvektor u'y ansteigt.

Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen. Wie kommt es das die Kugel dann schneller wird? Sollte sie nicht eher langsamer werden?

mojorisin schrieb:Ja, aber was da berechnet wurde ist nicht dasselbe wie in dem GE in deinem Buch.

Hä - was hat denn ein Buch auf das du dich berufen hast mit deinen Behauptungen zu tun.
Abgesehen davon wirst du doch wohl kaum die dort auf Seite 207 aufgeführte Gleichung, auf die du dich berufen hast, nicht als physikalisch unsinnig erklären oder.

@pluss

pluss schrieb:Abgesehen davon wirst du doch wohl kaum die dort auf Seite 207 aufgeführte Gleichung, auf die du dich berufen hast, nicht als physikalisch unsinnig erklären oder.

Das war im August letzen Jahres, völlig anderer Kontext, als es darum ging wie Objekte betrachtet mit unterschiedlichen Relativgeschwindigkeiten denselben Impuls haben und damit Auswirkung haben können:
Beitrag von mojorisin (Seite 16)

Und natürlich ist die Formel nicht unsinnig aber auch nur wenn man sie richtig anwendet. Dennoch beziehst du dich eindeutig in deinem angeblich Widerspruch auf genau das Experimen aus dem Buch das du hier auch reingestellt hast. Das ist aber etwasd anders als das was wir hier ausgemacht haben.

Ähnlich zum Buch ist aber mein Spoiler oben.

mojorisin schrieb:Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen. Wie kommt es das die Kugel dann schneller wird? Sollte sie nicht eher langsamer werden?

Bitte nicht ignorieren.

@mojorisin

mojorisin schrieb:Bitte nicht ignorieren.

Das kannst Du wohl vergessen, er spielt offenkundig einfach nicht fair und windet sich wie ein Schleimaal. Er fabuliert immer von Deinen und meinen Widersprüchen, die wir mal aufklären sollen, wir zeigen es gibt keine er macht den Kopf dicht.

Dann zeigt man aber die wahren Widersprüche auf, die eben bei ihm liegen, wie das er behauptet u_x = 0,9 c und nicht wie es richtig ist u_x = 0,392 c.

Er verweigert sich über ein halbes Jahr nun schon die einfachsten elementarsten Grundlagen mal zu lernen, zu begreifen, wie das mit dem zweiten System nun genau ist und dass eben auch hier in seinem "neusten" GE der Läufer sich im System des Bahndamms mit u_x = 0,392 c bewegt und sich die 0,9 c im System des Zuges gegeben sind, eben u'_x = 0,9 c.

Ich belege ihm das sogar mit seiner eigenen Gleichung, seiner Rechnung, so wie er selber zuvor mal u_x ausgerechnet hat. Da hat er auch erst, mit seiner falschen Formel, die Gesamtgeschwindigkeit ausgerechnet, und dann eben u_x und genau diesen Weg zeige ich ihm, aus dem ergibt sich eben seine u_x = 0,9 c sind falsch und richtig sind unsere u_x = 0,392 c.

Das ergibt sich wirklich genau so aus seinem eigenen Rechenweg und was kommt dazu nun von ihm?

Eben, nichts, er ignoriert es eben trumpt sich was zurecht.

Wenn @pluss hier wirklich fair und ehrlich an einer Klärung interessiert wäre, wie er ja immer wieder mal vorlügt, dann hätte er es aufgreifen müssen, hinterfragen, sich dazu äußern.

Tatsache ist, er hat bisher noch immer nicht begriffen, dass man nur dann "relativistisch" was rechnet, wenn es zwei zueinander bewegte Systeme gibt und man Größen in eben beiden angegeben hat und diese nun nur in einem haben möchte.

Er rafft einfach nicht, dass es nichts relativisches zu rechnen gibt, wenn es da nur Größen in einem einzigen System gibt.

Er unterstellt und dann da auf Überlichtgeschwindigkeit zu kommen, bei mir wenn ich mit dem Pythagoras rechne, rechnet aber selber genau mit diesem.

Also mal kann hier wirklich davon ausgehen, dass es hier @pluss nicht um die Sache selber geht, nicht darum die Dinge richtig zu begreifen.

mojorisin schrieb:Und natürlich ist die Formel nicht unsinnig aber auch nur wenn man sie richtig anwendet.

Ja, das ist wohl war. Nur leider bist du es der sie augenscheinlich nicht korrekt anwenden kann.

Das belege ich anhand deiner Excel-Tabelle. Aus ihr geht der Impuls hervor, der auf den Körper in Richtung der x-Achse übertragen wurde. Findet man in Feld "O12". Dort steht ein Betrag von 1,1318kgc. Als dieser Impuls auf den Körper übertragen wurde, hatte dieser eine Geschwindigkeit von 0,5c auf der y-Achse.

Aus dem übertragenen Impuls von 1,1318kgc folgt eine Geschwindigkeit von:

Aus u_x,vor können wir jetzt mit der Gleichung von Seite 207 u_x,nach berechnen:

Der übertragene Impuls auf der x-Achse kann folglich nicht zu u_x,nach=0,7c führen. Warum aber geht aus deiner Excel-Tabelle hervor das dort u_x,nach=0,7c (Feld "K12") erreicht wurde?

Ganz einfach, weil du den Impuls auf der y-Achse eingefroren hast. Um den daraus entstehenden Widerspruch zu umgehen, hast du folgende Begründung geliefert:

mojorisin schrieb am 10.02.2018:Im System S wird ganz einfach die Kugel immer schneller auf der x-Achse. Dadurch steigt im System S der Lorentzfaktor und daurch wird die Kugel da IMpulserhaltung gilt auf der y-Achse langsamer. Thats it.

Das ist natürlich Humbug. Nicht nur weil Masse keinen Einfluss auf eine Bestehende Geschwindigkeit ausüben kann, ist schließlich eine skalare Größe und keine vektorielle, sondern auch weil es im Widerspruch zu deiner propagierten Geschwindigkeit auf der x-Achse steht. Denn auch dort steigt die relativistische Masse mit der Geschwindigkeit an, lässt das in deinen Berechnungen zu u_x,nach jedoch unberücksichtigt. Stattdessen behauptest du einfach aus u_y,vor wird:

Das allerdings ist ein Zirkelschluss, da u_x,nach auf u_y,vor beruht. Du hast dir also einen zurecht geschummelt um auf

zu kommen.

Diese Mogelei ist bei mir nicht erforderlich. Siehst du an der unteren Excel-Tabelle. Nehmen wir die dortigen Beträge, also für den übertragenen Impuls auf der x-Achse Feld "O26" mit 1,3728kgc:

Aus dem übertragenen Impuls von 1,3728kgc folgt eine Geschwindigkeit von:

Aus u_x,vor können wir jetzt mit der Gleichung von Seite 207 u_x,nach berechnen:

Und genau das steht auch in Feld "K7".

P.S.: Hier kannst du nochmals nachlesen was genau auf Seite 207 steht, die Seite befindet sich dort im Spoiler.

@mojorisin

Sage mal, das Buch auf das sich @pluss so gerne beruft ist ja wohl mal so richtig grottenschlecht. Übler kann man wohl die SRT nicht beschreiben, ohne gutes Vorwissen wird man da aber noch tiefer in den Nebel geführt. Grundlegende Dinge werden so wirr und vermurkst beschrieben, wer hat das nur verbrochen?

---

@pluss

Mal wieder ist eine Gleichung von Dir falsch, wieder hast Du wo was abgeschrieben und dann umgemodelt und Murks fabriziert, von den Einheiten kommt da hinten c² und nicht c raus:

\textcolor{#F0E0D0}{(4.1.0)} \large \qquad \textcolor{#D0F0E0}{u_{x,\:nach}} \normalsize = \textcolor{#D0F0E0}{u_{x,\:vor}} \cdot \sqrt{\textcolor{#F0D0E0}{1} - \Big(\textcolor{#D0F0E0}{u_{y,\:nach}}\Big)^{2}} = \textcolor{#D0F0E0}{0,7494\:c} \cdot \sqrt{\textcolor{#F0D0E0}{1} - \Big(\textcolor{#D0F0E0}{0,357\:c}\Big)^{2}} = \textcolor{#D0F0E0}{0,7\:c}^\textcolor{#F0D0E0}{\:2}

Das liegt daran, dass der Term (im Buch) mit der Wurzel für den Gammafaktor ^-1 steht, auf der Seite 207 wird auch dort v in c angegeben und dann durch c geteilt, so kürzt sich c in der Wurzel raus. Du hast nun einfach c unterm Bruchstrich weggelassen, aber bei v dennoch dazu geschrieben. So bleibt von Term eben die Einheit c übrig und die multiplizierst Du noch mal mit c und das ergibt dann c².

Davon abgesehen steht auf der Seite nichts von v_nach und v_vor. Das ist mal wieder Deine ganz eigene "Interpretation" der Gleichung. Mathematisch und physikalisch zeigt die Gleichung auf Seite 207 einfach nur eine einfache LT einer Geschwindigkeit aus einem zum Beobachter bewegten System in das Ruhesystem des Beobachters. Also im GE eben aus dem System von Bob in das System von Alice.

Aber wenn @mojorisin nun nicht doch mal die Faxen mit Dir dicht hat, wird er Dir das wohl auch noch mal erklären.

Was ist nun mit dem Widerspruch den ich Dir aufgezeigt habe? Das ignorierst Du mal wieder wie üblich ... :D

@pluss

pluss schrieb:Der übertragene Impuls auf der x-Achse kann folglich nicht zu ux,nach=0,7c führen. Warum aber geht aus deiner Excel-Tabelle hervor das dort ux,nach=0,7c (Feld "K12") erreicht wurde?

0,7c ist vorgegeben nicht berechnet, abgesegnet von dir selbst.

mojorisin schrieb: mojorisin schrieb:
Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen. Wie kommt es das die Kugel dann schneller wird? Sollte sie nicht eher langsamer werden?

Bitte nicht ignorieren.

Bitte nicht ignorieren.

mojorisin schrieb:0,7c ist vorgegeben nicht berechnet, abgesegnet von dir selbst.

Ich habe aber keinen Impuls vorgegeben, den hast du selbst berechnet.
Dein berechneter Impuls führt jedoch nur zu 0,649c, erfüllt also nicht die Vorgabe.

@mojorisin
@nocheinPoet
Unglaublich das ihr Euch immer noch veralbern lasst von ihm. :) Er hat schon vor über einem Monat eingesehn das es völlig egal ist von welcher Uhr das Lichsignal ausgesendft wird und das es eben keinen Unterschied mach welche Art Uhr ich dafür als Zeitmesser zu Hilfe nehme. Dieses Impulsgelaber ist doch nur Ablenkung und ihr spielt noch fein mit. :)

@pluss

pluss schrieb:Das belege ich anhand deiner Excel-Tabelle. Aus ihr geht der Impuls hervor, der auf den Körper in Richtung der x-Achse übertragen wurde.

Die zweite Hälfte war extra für dich gemacht um die Auswirkungen einer konstanten Geschwindigkeit u_y zu demonstrieren, und jetzt greifst du deine eigenen Vorhersagen an? AUserdem gab es da noch gar keine Stoß also auch kein vor und nach. Leider scheinst du dich nicht mehr daran erinnern zu können. Auch sind die Lorentzfaktoren zwischen Impuls und GEschwindigkeiten unterschiedlich. Lorentzfaktoren für GEschwindigkiten ergeben sich aus der Reltivgeschwindigkeiten zwischen S und S', während der Lorentzfaktor für den IMpusl sich aus der GEsamtgeschwindigkeit ergibt sprich Realtivgeschwindigkeit zwischen S und Ruhesystem Kugel. Daher macht deine Rechnung schlicht keinen Sinn.


Trotzdem würde mich hier noch ein Antwort von dir interessiern den du hast ja gesagt 3D GEschwindigkeitenm sind für dich kein Problem:

mojorisin schrieb:Aus Sicht von Alice bewegt sich Bob's Rakete mit 0,95c auf der x-AChse. Aus Bob's Sicht bewegt sich die Kugel mit 0,95c auf der y-AChse. Aus der Kugel Sicht bewegt sich eine Ameise mit 0,95c auf der z-Achse.

Welche Geschwindigkeit hat die Ameise aus Sicht von Alice?

By the way:

mojorisin schrieb:mojorisin schrieb:
mojorisin schrieb:
Also wenn die Zeit in S' langsamer vergeht, dann müsten ja auch logischerweise alle physikalischen Vorgänge verlangsamt ablaufen. So wenn wir z.B. Zeitlupe ablaufen lassen. Wie kommt es das die Kugel dann schneller wird? Sollte sie nicht eher langsamer werden?

Bitte nicht ignorieren.

McMurdo schrieb:Unglaublich das ihr Euch immer noch veralbern lasst von ihm. :) Er hat schon vor über einem Monat eingesehn das es völlig egal ist von welcher Uhr das Lichsignal ausgesendft wird und das es eben keinen Unterschied mach welche Art Uhr ich dafür als Zeitmesser zu Hilfe nehme. Dieses Impulsgelaber ist doch nur Ablenkung und ihr spielt noch fein mit. :)

Also als stiller Mitleser dessen Mathe Kenntnisse über die Dekaden hin etwas gelitten haben, muss ich sagen das ich hier von @mojorisin und @nocheinPoet viel gelernt habe. Kann und will nicht alle Formeln nachvollziehen, aber gerade die verbalen Erklärungen helfen mir einiges von dem Thema besser zu verstehen. Ohne es jetzt berechnen zu wollen. Gott bewahre
Insofern, bitte weitermachen. Ich bin sicher (oder besser ich hoffe :D), es geht hier noch mehr Leute so

@pluss

Mal so am Rande, Deine dritte Rechnung ist vom Ergebnis falsch:

\textcolor{#F0E0D0}{(4.1.3)} \large \qquad \textcolor{#D0F0E0}{u_{y, \: nach}} \normalsize = \textcolor{#D0F0E0}{u_{y, \: vor}} \cdot \sqrt{\textcolor{#D0F0E0}{1} - \Big(\textcolor{#D0F0E0}{u_{x, \: nach}}\Big)^{2}} = \textcolor{#D0F0E0}{0.5} \cdot \sqrt{\textcolor{#D0F0E0}{1} - \Big(\textcolor{#D0F0E0}{0,7494}\Big)^{2}} \neq \textcolor{#F0D0E0}{0,357\:c}

Das richtige Ergebnis der Gleichung lautet \textcolor{#D0F0E0}{0,331\:c}, rechnest Du gar nicht was Du da aufschreibst auch mal aus? Du musst schon \textcolor{#D0F0E0}{u_{x, \: nach}} = \textcolor{#D0F0E0}{0,7\:c} richtig einsetzen, wenn Du da auf \textcolor{#D0F0E0}{0,357\:c} kommen willst.

---

---

So, auch wegen den mehr stillen Lesern hier zeige ich mal eben auf, was @pluss da wieder für einen Unfug auf der Seite 207 im Buch verstanden hat, ich zitiere mal den Teil:

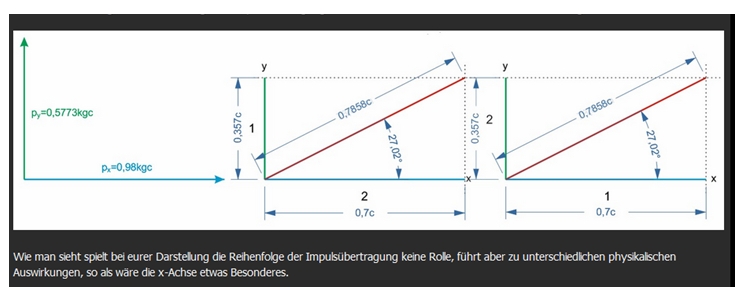
… Nehmen wir an, wir (äußerer Beobachter) - [nennen wir den mal Alice im Ruhesystem S] - habe einem Körper einen Kraftstoß in Richtung x-Achse versetzt, der zu einer Geschwindigkeit von 0,6 c geführt hat.

Der äußere Beobachter Alice misst in ihrem Ruhesystem S einen Körper mit v = \textcolor{#D0F0E0}{0,6\:c} auf der x-Achse.

Nun versetzt eine Person, die mit dem Körper reist - [nennen wir diese Person mal Bob im Ruhesystem S'] - dem Körper den gleichen Kraftstoß auf der y-Achse.

Der, mit dem Körper reisende Beobachter, also Bob gibt dem Körper einen gleichgroßen Stoß auf der y-Achse, dadurch bewegt dieser sich im Ruhesystem S' von Bob mit v = \textcolor{#D0E0F0}{0,6\:c} auf der y-Achse.

Wegen der Zeitdilatation läuft der zweite Vorgang aus Sicht des äußeren Beobachters - [also für Alice in S] - langsamer ab, aber das Ergebnis (0,6 c in Richtung der y-Achse) sollte gleich sein, könnte man auf den ersten Blick meinen.

Das ist ein wichtiger Teil, der Autor erklärt, auch wenn Bob in seinem Ruhesystem S' den Körper auf der y-Achse mit v = \textcolor{#D0E0F0}{0,6\:c} misst, beobachtet und misst Alice in ihrem Ruhesystem S, als äußerer Beobachter diesen Vorgang, also eben genau diese Bewegung, langsamer.

Alice misst also die Geschwindigkeit des Körpers auf der y-Achse in ihrem Ruhesystem S mit v < \textcolor{#D0F0E0}{0,6\:c}

Der Körper gewinnt in Richtung der y-Achse aber nur insgesamt 0,48 c hinzu - [gemessen in Ruhesystem S von Alice] -, da die bereit weiter vorn entwickelte Formel gilt:

\textcolor{#F0E0D0}{(4.0.0)} \qquad \textcolor{#D0F0E0}{w_y} \normalsize = \textcolor{#D0E0F0}{u_y} \times \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \textcolor{#D0E0F0}{0,6} \times \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{0,6}^{\:2}} {1^{\:2}} } = \textcolor{#D0E0F0}{0,6} \times 0,8 = \textcolor{#D0F0E0}{0,48}

So, dass ist die originale Gleichung aus dem Buch von Seite 207, kann mit hier im Spoiler nachlesen. Ich habe aber schon mal die Variablen und Größen entsprechend der Systeme, in denen sie gemessen werden, eingefärbt. Der gute Bob misst immer alles in seinem Ruhesystem S' und die liebe Alice misst immer alles in ihrem Ruhesystem S.

Die Gleichung hat nicht mit \textcolor{#D0F0E0}{u_{y, \: nach}} und \textcolor{#D0E0F0}{u_{y, \: vor}} zu tun, so wie @pluss das behauptet. Die Gleichung zeigt einfach nur die Lorentztransformation einer Geschwindigkeit, hier eben von der Geschwindigkeit des Körpers auf der y-Achse, welche Bob in seinem Ruhesystem S' misst. In der Gleichung wird diese nun aber mit \textcolor{#D0E0F0}{u_y} bezeichnet, im GE hier wäre die richtige Bezeichnung hingegen \textcolor{#D0E0F0}{u'_y}.

Der Autor berechnet hier einfach nur die Geschwindigkeit des Körpers auf der y-Achse im Ruhesystem S des äußeren Beobachters Alice mit \textcolor{#D0F0E0}{u_y} = \textcolor{#D0F0E0}{0,48\:c}.

---

Nun schauen wir uns mal den Term mit der Wurzel genauer an:

\sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{0,6}^{2}} {c^{\:2}} } = 0,8


Den Lesern hier dürfte das sicher schon aufgefallen sein, es handelt sich hier einfach nur um den Kehrwert des Lorentzfaktors bei einer Geschwindigkeit zwischen beiden Systemen von v = \textcolor{#D0F0E0}{0,6\:c} .

\gamma^{\:-1} = \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{0,6}^{2}} {c^{\:2}} } = 0,8


Kann man hier nachlesen, wenn der Kehrwert nun 0,8 ist, folgt daraus der Lorentzfaktor selber mit \gamma = 1,25

---

Somit zeigt die von @pluss genannte Gleichung nichts anderes, als das was wir ihm hier schon über ein halbes Jahr erklären, einfach nur die Transformation einer senkrechten Geschwindigkeit aus einem zum Beobachter bewegten Systems S' (hier eben das von Bob) in das Ruhesystem S des Beobachters (hier dann eben Alice):

\textcolor{#D0F0E0}{u_y} = \textcolor{#D0E0F0}{u'_y} \cdot \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \textcolor{#D0E0F0}{u'_y} \cdot \gamma^{\:-1} = \textcolor{#D0E0F0}{0,6\:c} \cdot 0,8 = \textcolor{#D0F0E0}{0,48\:c}

---

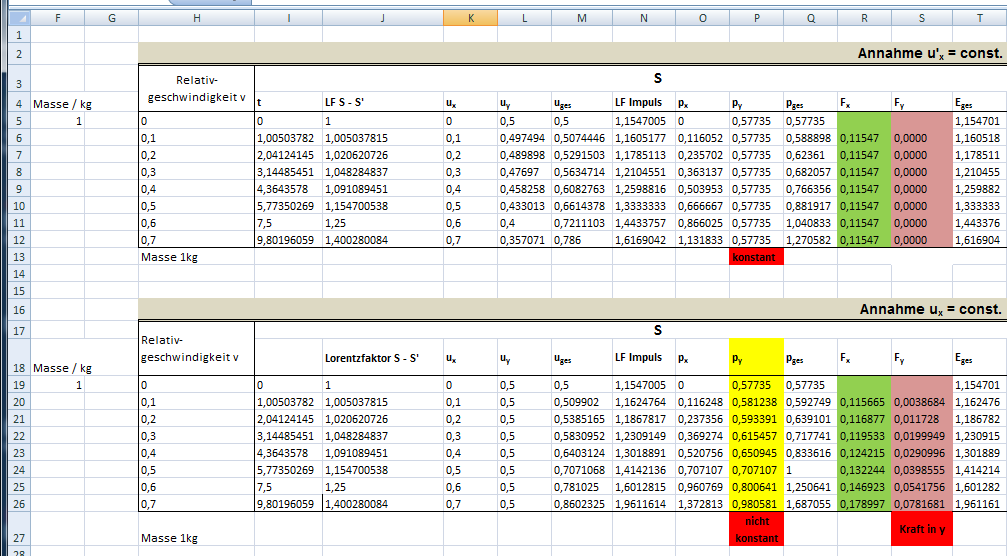
Da braucht es also nicht das Buch und die Gleichung von Seite 207, seit über einem halben Jahr rechnen wir das hier im Team nun @pluss eben genau so vor. Nehmen wir mal die Werte aus dem GE:

\textcolor{#D0F0E0}{u_y} = \textcolor{#D0E0F0}{u'_y} \cdot \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_x}^{2}} {c^{\:2}} } = \textcolor{#D0E0F0}{u'_y} \cdot \gamma^{\:-1} = \textcolor{#D0E0F0}{0,5\:c} \cdot 1,4^{\:-1} = \textcolor{#D0F0E0}{0,357\:c}


Damit ist gezeigt und belegt, @mojorisin und ich sagen nichts anderes, als auch im Buch steht (zumindest von der Mathematik, wir erklären es ganz sicher besser), es gibt eben keinen Widerspruch zu dem was dort gerechnet wird und dem was wir hier über ein halbes Jahr dem guten @pluss rauf und runter vorrechnen.


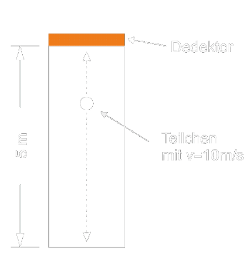
Ich zeige das noch mal mit dem letzten tollen GE von @pluss wo er über einen fallenden Zug rennt:

\textcolor{#D0F0E0}{u_x} = \textcolor{#D0E0F0}{u'_x} \cdot \sqrt{\textcolor{#F0E0D0}{1} - \frac {\textcolor{#D0E0F0}{v_y}^{2}} {c^{\:2}} } = \textcolor{#D0E0F0}{u'_x} \cdot \gamma^{\:-1} = \textcolor{#D0E0F0}{0,9\:c} \cdot 2,294^{\:-1} = \textcolor{#D0F0E0}{0,3923\:c}


Achtung, hier sind beide Achsen vertauscht, der Zug ruht im System S' und fällt gegenüber S auf der y-Achse, somit errechnet sich daraus der Gammafaktor mit \gamma = 2,294 und in dem System S' läuft dann @pluss mit \textcolor{#D0E0F0}{u'_x} = \textcolor{#D0E0F0}{0,9\:c} auf der x-Achse über den Zug. Im System S' ist nun natürlich dann eben auch genau diese Geschwindigkeit auf \textcolor{#D0F0E0}{u_x} = \textcolor{#D0F0E0}{0,3923\:c} verlangsamt.

---

So, hier zeigt sich wieder ein weiteres mal, @pluss verstehst nicht das was er wo liest, er reißt es dann raus, ändert Namen von Variablen, lässt mal was weg und fügt anderes hinzu. Hier hat er die ganz normale LT einfach umgemodelt und was von "vor" und "nach" als Index an die Bezeichner geschraubt.

Die Frage ist wirklich, was das soll, er muss doch wissen, @mojorisin und mich kann er damit nicht täuschen, wir erkennen das auf den ersten Blick. Soll man nun wirklich glauben, er selber erkennt es nicht, weiß wirklich gar nicht was er da macht, versteht den Text im Buch, gut er ist wirklich grottenschlecht, so falsch?

Es ist doch so, wir erklären das nun wirklich schon über ein halbes Jahr, der Thread selber füllt fast schon ein gutes Buch.

Wir haben es ihm erklärt, vorgerechnet, verlinkt, auf Wikipedia zitiert, nun finden sich unsere Aussagen selber in seiner eigenen Quelle, es wird doch nun wirklich mal Zeit hier Farbe zu bekennen und den eigenen Irrtum offen zuzugeben.

Oder?

Auch meine letzte Rechnung wo ich ihm zeigte, seine \textcolor{#D0F0E0}{u_x} = \textcolor{#D0F0E0}{0,9\:c}[/color] sind falsch, nach seiner eigenen Rechnung kommt da eben \textcolor{#D0F0E0}{u_x} = \textcolor{#D0F0E0}{0,3923\:c}[/color] raus. Und auch die Bezeichnung, für die Geschwindigkeit selber im Ruhesystem des Zuges ist falsch, richtig ist lautet die eben \textcolor{#D0E0F0}{u'_x} = \textcolor{#D0E0F0}{0,9\:c}[/color].

Und genau dazu schweigt er nun, er ignoriert eben immer, wenn man ihm seine Fehler und Widersprüche aufzeigt.

@nocheinPoet
Hi
Hast Du eigentlich die von dir genannten Professoren oder was auch immer wie angekündigt zu dieser Diskussion hier befragt?

Ich lese auch mittlerweile nur still und überfliegend mit, ist mir zu kuddelmuddelig geworden.

Ihr solltet echt noch mal ganz von vorne anfangen, pluss muss ganz simpel schreiben was er wozu meint, und der Gegenpart genau so simpel was da nicht stimmt. Und dann kann man in aller Ruhe wieder anfangen alles auseinander zu klabüstern.

Und dann wäre es ja echt cool, wenn Du nocheinPoet, die von dir genannten Gelehrten dazu bewegen könntest, dem ganzen hier beizuwohnen.

Ich erwarte nichts, aber das fänd ich echt toll :-)

@skagerak

Nun ja, fachlich ist das Thema schon seit Monaten geklärt, da gab es nie Zweifel, man kann es ja auch überall richtig nachlesen. Es ist einfach eben so, dass @pluss sich hier verweigert seinen Fehler und Irrtum zuzugeben.

Angefangen hat er ja mit einer mechanischen Uhr, seiner Schiffsuhr von John Harrison und seiner "Kugeluhr" ...

pluss schrieb am 02.07.2017:

Würde man nun noch zur Zeitmessung die Schiffsuhr von John Harrison, oder meine vorgeschlagene Uhr, heranziehen, ergeben sich keine (signifikanten) Gangunterschiede zwischen den Uhren bewegter und ruhender Beobachter.

Da war der Aufbau eines Beispiels aber so trivial und für jeden verständlich, dass es nicht genug Fluchtraum zum Tricksen für @pluss gab, und darum kam auf mal eine Reihenfolge für den Start der Uhr und der Rakete hinzu.

Auf mal war es entscheidend, dass die Uhr erst gestartet wird, nachdem die Rakete selber beschleunigt wurde und ihre Geschwindigkeit erreicht hatte. Nur dann, so @pluss, würde seine Behauptung nun noch gelten, nur dann würde die entsprechende Uhr nicht dilatieren.

Würde der Astronaut hingegen seine Uhr erst starten, wenn die Rakete schon beschleunigt wurde, dann würde sie so dilatieren, wie es eben die SRT auch richtig beschreibt.

Und dann kam aufmal die Nummer mit den Impulsen dazu, auf einmal waren Geschwindigkeiten so nicht mehr alleine genug, nein da muss die Beschleunigung und der Impuls berechnet werden.

Ja echt wo schon recht lustig auch. :D

---

Zu so einem Mumpitz findet sich natürlich nichts in der Fachliteratur, waren wohl mehr die Lustigen Taschenbücher und Fix und Foxi Hefte, die er dazu gelesen hat, er behauptet dazu hingegen über sich:

pluss schrieb am 07.02.2018:Wenn du der Ansicht bist das sich der Geschwindigkeitsvektor u_y ändert, dann solltest du wissen welche physikalische Gesetzmäßigkeit dafür verantwortlich ist und auch die Gleichungen zur Lösung des Problems kennen. Aber nicht jemanden Fragen, der davon überzeugt ist das sich der Geschwindigkeitsvektor u_y nicht verändert, weil er nach durchforsten von 11 Fachbüchern zur SRT und ART, sowie 24 Werken aus der Fachliteratur über Mechanik und Kinetik nicht ansatzweise etwas finden konnte was darauf hinweist das deine Ansicht zutreffend sein könnte.

Schon eine Leistung, mit "jemanden" meint @pluss natürlich sich selber. Ist ja nun so, für diese "Frage" braucht es max. fünf Minuten mit Google und sie ist beantwortet. Die braucht man auch nur dann, wenn man bis dato noch nichts von der SRT gehört hat.

Also so jemand ist hier nun das Gegenüber. Meine Idee mit der Mail war, diesen jemand da zu helfen, geht aber nur, wenn er dazu bereit ist, sich einbringt und sich an der Formulierung so einer Mail beteiligt.

Schreibe ich nun einfach nur selber etwas, wird @pluss jede Antwort ignorieren, tricksen, behaupten, die Frage war falsch gestellt und so weiter.

Man sieht es doch auch gerade wieder hier ganz aktuell, er liegt falsch, richtig, ich rechne es ihm vor, sogar mit seiner eigenen Gleichung und er schaltet einfach ab und ignoriert alles was dazu kommt.

Die Zielsetzung hier ist eine andere, ihm geht es nicht, so wie er immer vorgibt, darum die Dinge richtig zu begreifen, im Gegenteil, er will einfach nur Recht behalten, auf keinen Fall einen Irrtum zugeben müssen.

@McMurdo | @TunFaire | @skagerak | @delta.m und auch @pluss - da es Dich insbesondere betrifft.


Vor kurzen fragte mich @pluss nach einer Rechnung:

pluss schrieb am 10.03.2018:Die Frage war "wie werden ebene zu senkrechten und senkrechte zu ebenen Geschwindigkeiten relativistisch korrekt addiert".

Danach hatte er schon öfter gefragt und ich hatte diese ebenso auch ihm schon öfter beantwortet und natürlich habe ich seine Frage ein weiteres mal beantwortet:

nocheinPoet schrieb am 25.02.2018:Hat man nur ein System, braucht man keine SRT, keine Transformation und somit gibt es da auch kein "relativistische" Addition von irgendwelchen Geschwindigkeiten. Die Addition ist einfach ganz normale Vektorrechnung, und wenn da zwei Geschwindigkeitsvektoren in einem rechten Winkel in einem System zueinander stehen, dann geht das über den Pytaghoras und das machst Du ja auch selber schon. Dennoch mal ein aktuelles Beispiel:

\textcolor{#F0E0D0}{(1.0.0)} \large \qquad |\textcolor{#D0F0E0}{u}| = \sqrt{\textcolor{#D0F0E0}{u_x}^{2} + \textcolor{#D0F0E0}{u_y}^{2}} = \sqrt{ (\textcolor{#D0F0E0}{0,5\:c})^{2} + (\textcolor{#D0F0E0}{0,7\:c})^{2}} = \textcolor{#D0F0E0}{0,86\:c}

---

Worauf er dann mal wieder aus der Rolle fiel und mir entgegnete:

pluss schrieb am 10.03.2018:Du meinst den Bullshit hier: ... Bullshit deshalb, weil du so auf Überlichtgeschwindigkeit kommst wenn z.B. \parallel u_x = 0,75 + \bot u_y=0,75c addiert werden sollen. Wenn Pythagoras, dann den relativistischen bitte. Also, ich Frage dich nochmals: ... Wenn du die Frage nicht korrekt beantworten kannst, dann sag es einfach.

Nun gut, ich rechne bei ihm ja nicht mehr mit Verständnis oder Einsicht, aber wenn man sich dann mal dazu im Vergleich einen eigenen Beitrag von @pluss anschaut, ein wenig zurück:

pluss schrieb am 10.03.2018:Kann auch die Lösung der weiter vereinfachten Frage aufzeigen:

pluss schrieb am 10.03.2018:Ein Körper A bewegt sich im System S mit der Geschwindigkeit u = {u_x = 0 , u_y = 0,5c}. Wie sieht der Geschwindigkeitsvektor von A im System S aus, wenn der Körper auf der x-Achse auf u_x = 0,7 c beschleunigt wurde?

Lösung:

u_x = 0,7c
u_y =0,5c

\large |\textcolor{#D0F0E0}{u}| = \sqrt{\textcolor{#D0F0E0}{u_x}^{2} + \textcolor{#D0F0E0}{u_y}^{2}} = \sqrt{ (\textcolor{#D0F0E0}{0,5\:c})^{2} + (\textcolor{#D0F0E0}{0,7\:c})^{2}} = \textcolor{#D0F0E0}{0,86\:c}

verwundert seine Antwort dann doch.

---

Also @pluss nimmt gleiche Werte wie ich, gleiche Bezeichner, gleiche Rechnung, gleiche Formel und kommt zum gleichen Ergebnis wie ich. Aber meine Rechnung und meine Antwort bezeichnet er als Bullshit, da könnte man ja auf Überlichtgeschwindigkeit kommen.

Wo soll denn da nun der Unterschied zu seiner Rechnung sein?

Und genau das ist der Punkt, wegen solcher Aktionen hier von @pluss sage ich, er spielt einfach nicht fair, er verarscht hier die anderen User.

Der Link zu dem Beitrag von @pluss mit der Rechnung war falsch, hier der richtige: Beitrag von pluss (Seite 83)