@delta.m Ist die alte Nummer von
@pluss klar hätte er es auch gleich richtig mathematisch formulieren können. Nebenbei habe ich heute morgen ein "in" überlegen gehabt, inzwischen hat er es ja auch noch bildlich dargestellt. Der Läufer rennt also "in" Fahrtrichtung des Zuges und nicht diesem entgegen. Ist die alte Geschwindigkeitskaskade, habe ich hier schon ein paar mal beschrieben gehabt. Und wie immer schraubt er die Bilder riesengroß, wo doch so was schon reicht:
 Original anzeigen (0,2 MB)
Original anzeigen (0,2 MB)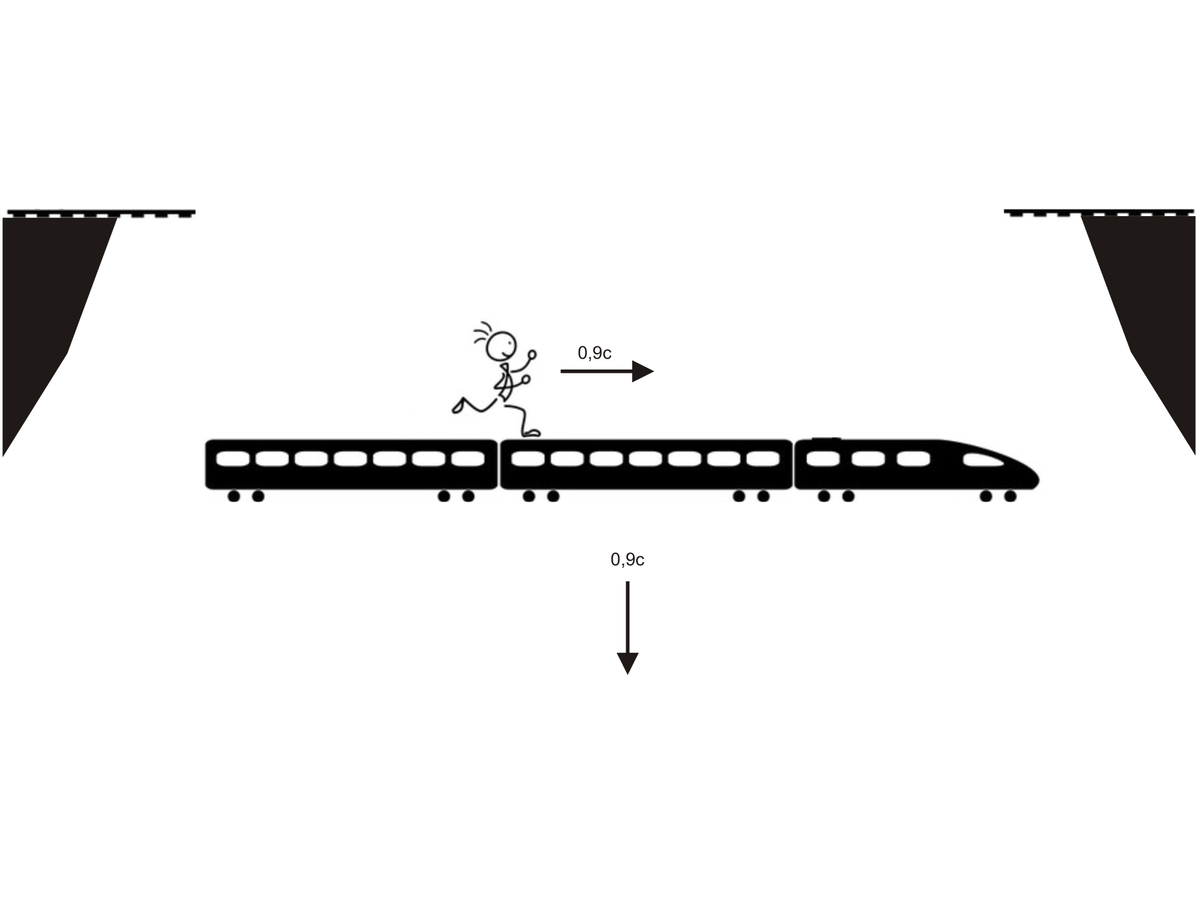 Original anzeigen (0,3 MB)
Original anzeigen (0,3 MB)Und wieder schreibt er Unfug, dazu in Prosa:
 pluss schrieb:Aus Sicht von Pluss ist der Zug unbewegt, ...
pluss schrieb:Aus Sicht von Pluss ist der Zug unbewegt, ...
Schwachsinn, mal wieder richtig falsch, einfachste Dinge kannst Du nicht richtig beschreiben, selbst mit eigener Zeichnung nicht.
:D Aus Sicht von Pluss ist der Zug mit 0,9 c bewegt und ganz sicher nicht unbewegt. Wäre er aus Sicht von Pluss unbewegt, würde Pluss auf dem Zug stehen. Denn der bewegt sich dann ja aus Sicht von Pluss nicht. Raff endlich "aus Sicht von ..." bedeutet, "im Ruhesystem von ... gemessen". So und weiter geht es mit Falschem:
 pluss schrieb:... der Zug ist sein Inertialsystem.
pluss schrieb:... der Zug ist sein Inertialsystem.
Unfug, der Zug ist ein Körper ein Objekt, kein Koordinatensystem, nichts frei definiertes und fiktives. Ein Inertialsystem ist etwas nicht materielles. Du meinst, der Zug ruht in einem Inertialsystem, das ist dann das Ruhesystem des Zuges, aber nicht das Ruhesystem von Pluss.
Der Zug ist nur im Ruhesystem des Zuges unbewegt, sicher nicht im Ruhesystem von Pluss.
Also sehr schön zeigst Du hier wieder einmal, Du verstehst nicht mal die Grundlagen, bist nicht mal in der Lage ganz einfache Dinge, die Du schon selber nun aufgezeichnetst hast, richtig mathematisch und physikalisch zu beschreiben, mir wäre das ja echt so was von peinlich ...
:D
 pluss schrieb:Zum zweiten Teil, der eigentlichen Frage: Der Zug, auf dem Pluss aus seiner Sicht mit 0,9 c läuft, fällt nun gradlinig und senkrecht zum Wagon auf dem Pluss läuft mit 0,9c von der Brücke. Mit anderen Worten: Der Zug fällt mit 0,9c nach unten. Pluss läuft nach wie vor mit 0,9c relativ zum Zug auf dem Zug.
pluss schrieb:Zum zweiten Teil, der eigentlichen Frage: Der Zug, auf dem Pluss aus seiner Sicht mit 0,9 c läuft, fällt nun gradlinig und senkrecht zum Wagon auf dem Pluss läuft mit 0,9c von der Brücke. Mit anderen Worten: Der Zug fällt mit 0,9c nach unten. Pluss läuft nach wie vor mit 0,9c relativ zum Zug auf dem Zug.
Andere Worte machen es nicht besser, wenn sie auch falsches wiedergeben. Systeme hatte ich ja schon benannt, der Zug bewegt sich also im Ruhesystem S'' von Pluss mit 0,9 c und ebenso bewegt sich Pluss im Ruhesystem S' des Zuges mit 0,9 c.
Aber ganz wichtig ist hier richtig anzugeben, in welchem System soll nun der Zug mit 0,9 c nach unten fallen?
Da gibt es keine Angabe zu, bleibt aber von der Logik nur S. Also im Ruhesystem S des Bahndamms soll sich der Zug nun mit u
x = 0,9 c auf der x-Achse bewegen. Und dann soll der Zug nun auch noch zusätzlich mit 0,9 c sich im Ruhesystem S des Bahndamms auf der y-Achse nach unten bewegen. Legen wir die y-Achse des Systems auch mal nach unten, dann bekommen wir da weiter einen positiven Wert für die Geschwindigkeit.
Damit haben wir dann beide Werte:
u
x = 0,9 c
u
y = 0,9 c
Und beschreibt
@pluss wieder, wie er wartet, etwas physikalisch unmögliches, um dann zu behaupten, die Gleichung sei falsch.
:DEs geht so einfach nicht. Der Zug kann sich in Summe immer nur mit v < c in einem System bewegen. Somit gilt:
√ (u
x² + u
y²) < c
Es bleibt dabei,
@pluss gibt hier physikalisch unmögliche Geschwindigkeiten vor. So etwas kann eben nie physikalisch in diesem Universum existieren. Geht ebenso wenig wie, ein Zug bewegt sich in S mit 0,9 c und soll seine Geschwindigkeit um 0,9 c erhöhen. Kann man zwar rechnen, gibt 1,8 c, ist aber physikalisch nicht möglich. Dass es physikalisch nicht möglich ist, bedeutet aber nicht, die Formel selber ist falsch.
Aus Falschem folgt eben Falsches, wenn man etwas unmögliches vorgibt, kommt eben auch recht wahrscheinlich etwas unmögliches raus.
Aber damit das noch wo dann Sinn ergibt kann man es etwas abändern,
@pluss erkennt wie wenig er von Physik versteht und springt von (zuvor aber stehend auf dem Zug) von dem Zug und der Brücke. Und nun fällt er im Ruhesystem S' des Zugs mit 0,9 c auf der y-Achse. Das ist dann also u'
y = 0,9 c und physikalisch möglich.
Jetzt hat man zwei Geschwindigkeiten in zwei Systemen und man kann die Geschwindigkeit von Pluss in S ausrechnen, mit der LT versteht sich. Der Gammafaktor bei 0,9 c beträgt 2,294 und somit fällt Pluss im Ruhesystem des Bahndamms mit 0,9 c
⋅ 2,294
-1 = 0,392 c. Also haben wir dann:
u
x = 0,900 c
u
y = 0,392 c
Und das geht nun auch mit dem Pythagoras:
|u| = √ (u
x² + u
y²) = √ ((0,9 c)² + (0,392 c)²) = 0,982 c
Nun ja, so geht es eben wenn man Ahnung hat und nicht wie Du durch den Nebel taumelt
@pluss ...
 pluss schrieb:Aus Sicht von Pluss ist der Zug immer noch unbewegt, der Zug ist sein Inertialsystem.
pluss schrieb:Aus Sicht von Pluss ist der Zug immer noch unbewegt, der Zug ist sein Inertialsystem.
Nett das Du den Unfug noch mal wiederholst so zum Ende.
:DBeides falsch, wenn der Zug aus der Sicht von Pluss unbewegt ist, dann muss Pluss auf dem Zug stehen. Oder er sitzt im Zug.
Und weiterhin ist der Zug kein Inertialsystem und auch ganz sicher nicht das von Pluss.
 pluss schrieb:Jetzt verstanden @delta.m und @nocheinPoet ?
pluss schrieb:Jetzt verstanden @delta.m und @nocheinPoet ?
Ich kann da nur für mich sprechen und ich habe nun verstanden, dass Du wirklich noch viel weniger Ahnung von Physik hast, als ich bisher dachte. Ich ging fälschlich doch wirklich davon aus, Du wüsstest, dass der Zug aus Sicht von Pluss bewegt ist, wenn er darüber rennt.
Bei Dir rennt aber wer über einen Zug und dennoch ist der Zug aus dessen Sicht unbewegt, toll, damit verstehst Du nun nicht mal mehr das was in der 2. Klasse üblich ist. Nie Sachkundeunterricht gehabt?
So, ich sehe noch eine Möglichkeit, wenn die gemeint ist, ist es aber wirklich grottenschlecht beschrieben, es kann sein, dass der Zug auf der Brücke angehalten haben soll. Wurde aber nicht erwähnt, wenn der vorher mit 0,9 c unterwegs ist, sollte dann im zweiten Fall schon explizit erwähnt werden, dass der Zug nun auf der Brücke erstmal steht, sich also nicht mehr mit 0,9 c auf der x-Achse bewegt.
Dann könnte weiter gemeint sein, dass sich nicht auf der y-Achse gegenüber dem Zug bewegt, dennoch ist es falsch zu sagen, aus Sicht von Pluss ist der Zug unbewegt, denn der bewegt sich ja unter den Füßen von Pluss mit 0,9 c hinweg.
Von der Rechnung ändert sich nun nichts groß, wir tauschen nur die Körper.
Im Ruhesystem S' des Zuges bewegt sich Pluss mit u'
x = 0,9 c und im Ruhesystem des Bahndamms fällt der Zug mit 0,9 c auf der y-Achse. Wir haben also:
u'
x = 0,9 c (Pluss bewegt sich mit 0,9 c im Ruhesystem S' des Zuges auf der x-Achse)
u
y = 0,9 c (Zug fällt mit 0,9 c im Ruhesystem S des Bahndamms auf der y-Achse)
Nun müssen wir eben u' nach u umrechnen, geht wieder mit der LT sieht dann so aus, der Gammafaktor bei 0,9 c beträgt 2,294 und somit rennt Pluss im Ruhesystem des Bahndamms mit 0,9 c
⋅ 2,294
-1 = 0,392 c auf dem Zug entlang.
Also haben wir dann:
u
x = 0,392 c (Pluss rennt mit dieser Geschwindigkeit in S über den Zug)
u
y = 0,900 c (Pluss fällt mit Zug mit dieser Geschwindigkeit in S von der Brücke)
Die Gesamtgeschwindigkeit von Pluss bekommt man wieder über den Pythagoras:
|u| = √ (u
x² + u
y²) = √ ((0,392 c)² + (0,9 c)²) = 0,982 c
Wie man sieht, so oder so, es gibt keine Überlichtgeschwindigkeit, wenn man es richtig rechnet und physikalisch nichts falsches vorgibt.
Und man erkennt, wenn
@pluss hier gleich einfach die Geschwindigkeitswerte in den Systemen richtig vorgegeben hätte, wäre es viel verständlicher gewesen und man hätte gleich rechnen können. Dieses unsinnige überflüssige Geschwafel in Prosa soll doch nur ablenken.
delta.m schrieb:Bis dahin konnte ich der Fragestellung noch folgen. Was danach folgt ist einfach nur ???
pluss schrieb:Ein Zug fährt mit 0,9c von links nach rechts aus Sicht eines am Bahnhof stehenden.
pluss schrieb:Auf einem der Wagons rennt der Pluss mit 0,9c aus seiner Sicht in Bezug zum Wagon in Fahrtrichtung des Zuges.
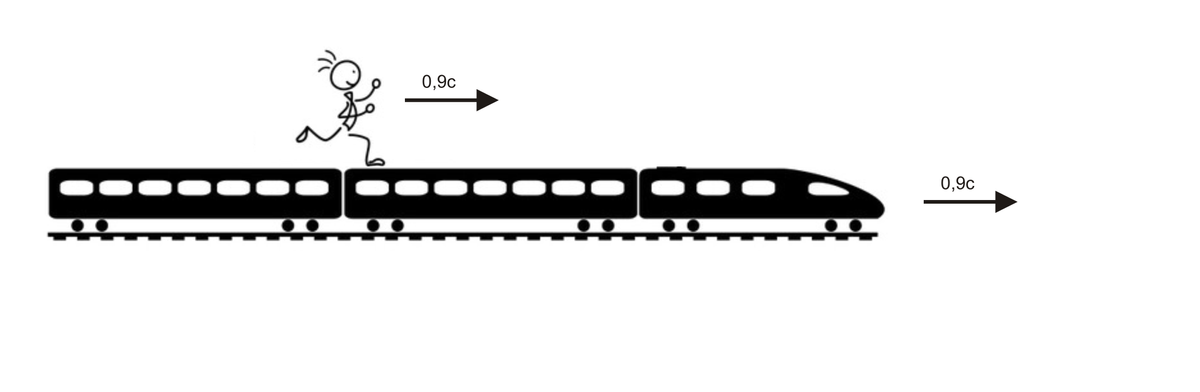 Original anzeigen (0,2 MB)
Original anzeigen (0,2 MB)pluss schrieb:Der Zug, auf dem Pluss aus seiner Sicht mit 0,9c läuft, fällt nun gradlinig und senkrecht zum Wagon auf dem Pluss läuft mit 0,9c von der Brücke.
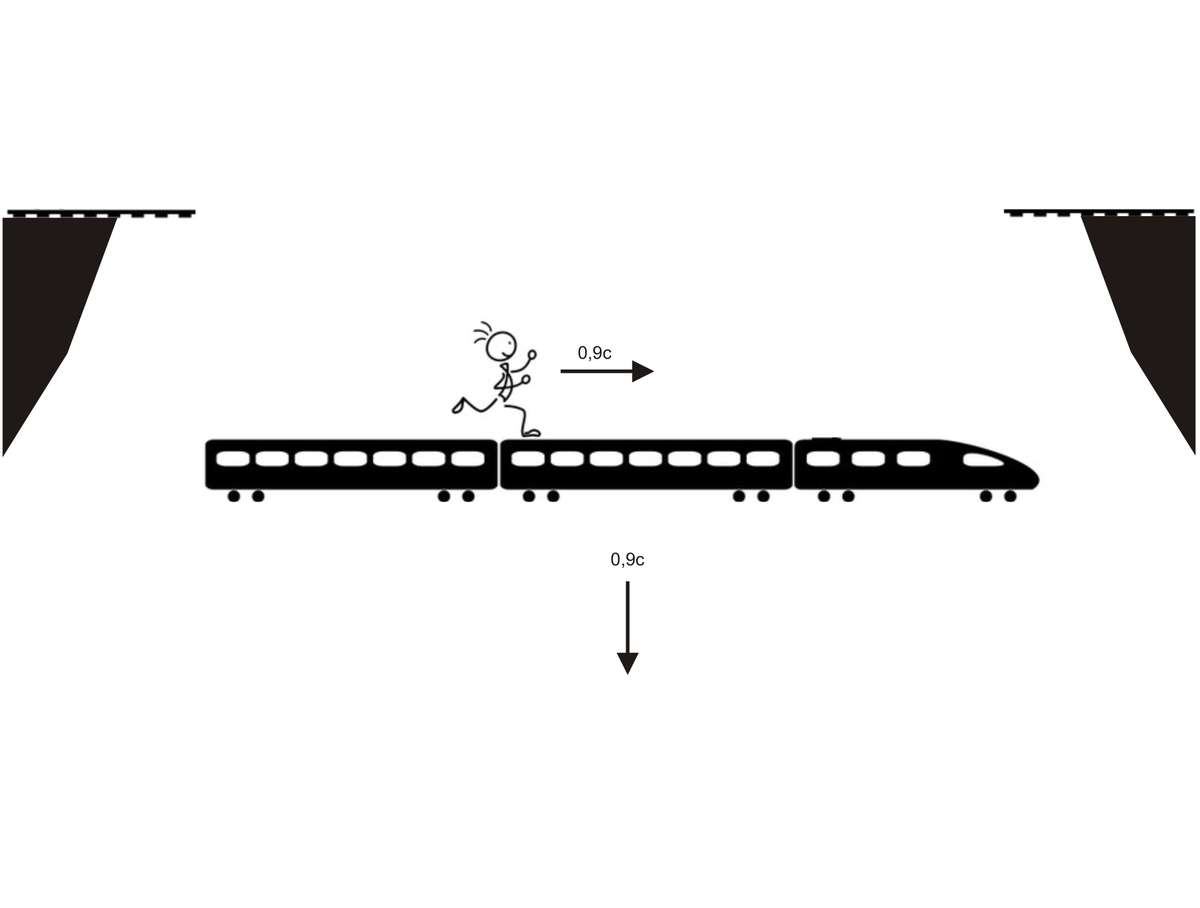 Original anzeigen (0,3 MB)
Original anzeigen (0,3 MB)







