mojorisin schrieb:Lass doch diesen armseligen Versuch die vorgestellte Methodik in den Dreck zu ziehen.
Das mache ich doch gar nicht. Ich bin nur der Ansicht das du mit allen deinen hier vorgestellten Lösungsversuchen deine These nicht stützen werden kannst. Ganz sicher möchte ich dich nicht davon abhalten alle durchzurechnen.
mojorisin schrieb: Bevor du mit den hier vorgestellten Gleichungen Zahlenspiele vollführst lies dich lieber gescheit ein.
Was denn, sind die Resultate deiner Ansicht nach falsch?
Oder nennst du es Zahlenspiele weil du hier nur noch Gleichungen ohne Werte und Resultate aufzeigst.
mojorisin schrieb:PS:
(1)
mojorisin schrieb:
Auf Seite 212 findest du exakt das was ich bei der Anwendung deiner Formeln die ganze Zeit anprangere:
Ist das Thema mit den von dir falsch genutzten Buchformeln durch?
Warum zitierst du den Teil vor der Gleichung nicht?
Ich mache es mal für dich:
Die Geschwindigkeit einer Kugel aus Sicht des äußeren Beobachters beträgt dann (Anwendung des relativistischen Pythagoras, siehe das Kapitel über die Kombination senkrechter Geschwindigkeiten):
w= \sqrt {v^2+u^2 - \frac {v^2 u^2} {c^2} }
v ist die Geschwindigkeit des Raumschiffs bzw. der Billardplatte aus Sicht des äußeren Beobachters, u ist die Geschwindigkeit der Billardkugel aus Sicht des Billardspielers. Die resultierende Geschwindigkeit w der Billardkugel aus Sicht des äußeren Beobachters soll im Folgenden mit w_{quer} bezeichnet werden. Eingesetzt ergibt sich:
w_{quer} = \sqrt {2 \cdot 0{,}6^2 - 0{,}36^2} = 0{,}768c
Der rot markierte Teil gefiel dir wohl nicht, weil, was ihr nicht kennt, gibt es nicht?
mojorisin schrieb am 13.03.2018:Es werden die GEschwindigkeiten aus zwei unterschiedlichen Inertialsystemen verwurstelt.
Verwurstelt? Was möchtest du denn damit zum Ausdruck bringen? Etwa das die Gleichung (relativistischer Pythagoras) Blödsinn ist, weil ihr ihn nicht kennt und euch das Resultat nicht gefällt bzw. nicht euren Erwartungen entspricht?
mojorisin schrieb am 13.03.2018:WEnn du aber schreibst:
\mathbf{u} =\sqrt{ u^2_x +u^2_y - \frac{u^2_yu^2_x}{c^2}}
dann sind das alles Geschwindigkeiten aus demselben INertialsystem. Das ist nicht was im Buch steht.
Ach, und du meinst weil es so nicht im Buch steht, muss mein Resultat falsch sein?
Bleibe mal bei deinem GE mit Kugel 1 und Kugel 2, darüber diskutieren wir hier schon über mehrere Seiten. In deinem Beispiel gibt es weder ein Raumschiff noch eine Billardplatte oder Billardspieler, sondern nur zwei Kugeln und einen äußeren Beobachter und somit auch nur u
x und u
y.
Deine Aufgabe verlangt das Kugel 1 ihren gesamten Impuls an Kugel 2 abgibt.
Der Impuls von Kugel 1 beträgt:
p_1= \gamma_{K_1} \cdot m_0 \cdot v_{K_1} = 1{,}4 \cdot 1kg \cdot 0{,}7c = 0{,}98kgc
Daraus folgt logischerweise eine Geschwindigkeit aus Sicht des äußeren Beobachters von:
u_x= \frac {c} {\sqrt {1+ \frac {m_0^2 c^2} {p_1^2} } }= \frac {1c} {\sqrt {1+ \frac {\left (1kg \right )^2 \cdot \left (1c \right )^2} { \left (0{,}98kgc \right )^2} } }=0{,}7c
Kugel 2:
p_2= \gamma_{K_2} \cdot m_0 \cdot v_{K_2} = 1{,}15 \cdot 1kg \cdot 0{,}5c = 0{,}5773kgc
Daraus folgt logischerweise eine Geschwindigkeit aus Sicht des äußeren Beobachters von:
u_y= \frac {c} {\sqrt {1+ \frac {m_0^2 c^2} {p_2^2} } }= \frac {1c} {\sqrt {1+ \frac {\left (1kg \right )^2 \cdot \left (1c \right )^2} { \left (0{,}5773kgc \right )^2} } }=0{,}5c
Nun wird die Geschwindigkeit der Kugel 1 auf Kugel 2 aus Sicht des äußeren Beobachters übertragen (durch einen vollkommen elastischen Stoß):
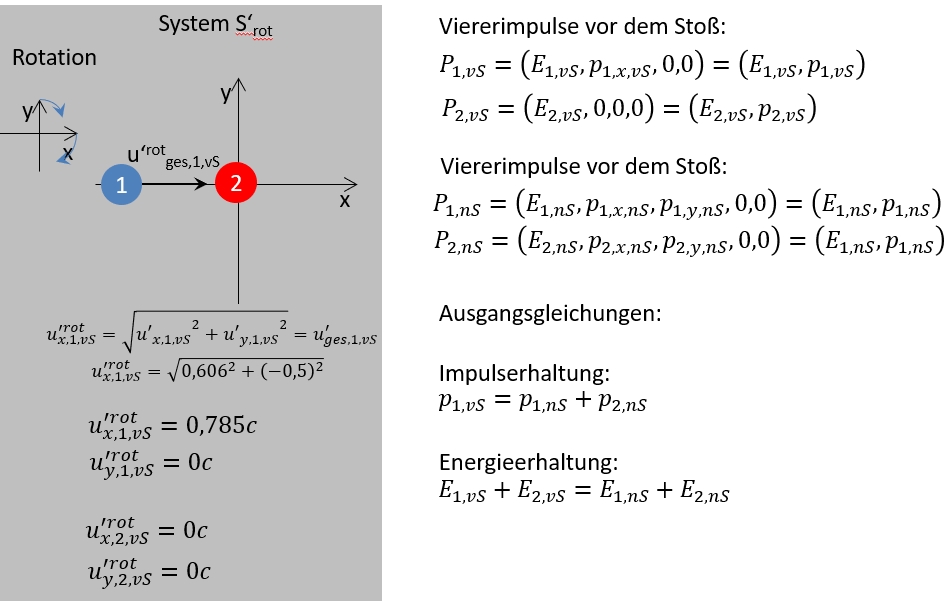
\mathbf u_2 = \sqrt {u_x^2 + u_y^2 - \frac {u_x^2 \cdot u_y^2} {c^2} } = \sqrt {\left (0{,}7c \right )^2 + \left (0{,}5c \right )^2 - \frac {\left (0{,}7c \right )^2 \cdot \left (0{,}5c \right )^2} {\left (1c \right )^2} }=0{,}7858c
Resultierende Geschwindigkeit auf der x-Achse aus Sicht des äußeren Beobachters:
u_{x_2}= \sqrt {\left (\mathbf {u_2} \right )^2 - \left (u_y \right )^2} = \sqrt {\left (0{,}7858c \right )^2 - \left (0{,}5c \right )^2}=0{,}606c
Resultierende Geschwindigkeit auf der y-Achse aus Sicht des äußeren Beobachters:
u_{y_2}= \sqrt {\left (\mathbf {u_2} \right )^2 - \left (u_{x_2} \right )^2} = \sqrt {\left (0{,}7858c \right )^2 - \left (0{,}606c \right )^2}=0{,}5c
Anders sieht es aus wenn die Addition der Geschwindigkeitsvektoren der Kugeln vertauscht wird, also Kugel 2 ihren Impuls vollständig an Kugel 1 durch einen vollkommen elastischen Stoß, aus Sicht des äußeren Beobachters, abgeben soll:
Kugel 1:
v_{K_1} \lbrace 0{,}7c , 0 , 0 \rbrace= 0{,}7c Kugel 2:
v_{K_2} \lbrace 0 , 0{,}5c , 0 \rbrace =0{,}5c Der Impuls von Kugel 1 beträgt:
p_1= \gamma_{K_1} \cdot m_0 \cdot v_{K_1} = 1{,}4 \cdot 1kg \cdot 0{,}7c = 0{,}98kgc
Daraus folgt logischerweise eine Geschwindigkeit aus Sicht des äußeren Beobachters von:
u_x= \frac {c} {\sqrt {1+ \frac {m_0^2 c^2} {p_1^2} } }= \frac {1c} {\sqrt {1+ \frac {\left (1kg \right )^2 \cdot \left (1c \right )^2} { \left (0{,}98kgc \right )^2} } }=0{,}7c
Kugel 2:
p_2= \gamma_{K_2} \cdot m_0 \cdot v_{K_2} = 1{,}15 \cdot 1kg \cdot 0{,}5c = 0{,}5773kgc
Daraus folgt logischerweise eine Geschwindigkeit aus Sicht des äußeren Beobachters von:
u_y= \frac {c} {\sqrt {1+ \frac {m_0^2 c^2} {p_2^2} } }= \frac {1c} {\sqrt {1+ \frac {\left (1kg \right )^2 \cdot \left (1c \right )^2} { \left (0{,}5773kgc \right )^2} } }=0{,}5c
Nun wird die Geschwindigkeit der Kugel 2 aus Sicht des äußeren Beobachters auf Kugel 1 übertragen:
\mathbf u_1 = \sqrt {u_x^2 + u_y^2 - \frac {u_x^2 \cdot u_y^2} {c^2} } = \sqrt {\left (0{,}7c \right )^2 + \left (0{,}5c \right )^2 - \frac {\left (0{,}7c \right )^2 \cdot \left (0{,}5c \right )^2} {\left (1c \right )^2} }=0{,}7858c
Resultierende Geschwindigkeit auf der y-Achse aus Sicht des äußeren Beobachters:
u_{y_1}= \sqrt {\left (\mathbf {u_1} \right )^2 - \left (u_x \right )^2} = \sqrt {\left (0{,}7858c \right )^2 - \left (0{,}7c \right )^2}=0{,}357c
Resultierende Geschwindigkeit auf der x-Achse aus Sicht des äußeren Beobachters:
u_{x_1}= \sqrt {\left (\mathbf {u_1} \right )^2 - \left (u_{y_1} \right )^2} = \sqrt {\left (0{,}7858c \right )^2 - \left (0{,}357c \right )^2}=0{,}7c
Nun lese nochmals Seite 207, hast dich ja auf die dort aufgeführte Gleichung berufen, und setze die obigen Beträge ein:
w_y=u_y \cdot \sqrt {1- \frac {u_x^2} {c^2}} =0{,}5c \cdot \sqrt {1- \left (\frac {0,7c} {1c} \right )^2}=0{,}357c
w_x=u_x \cdot \sqrt {1- \frac {u_y^2} {c^2}} =0{,}7c \cdot \sqrt {1- \left (\frac {0,5c} {1c} \right )^2}=0{,}606c
Wie du siehst kommt der gleiche Betrag heraus. Was du nicht verstehst und damals schon mit diesem Kommentar klar zum Ausdruck brachtest:
mojorisin schrieb am 14.02.2018:Wieso erzielt die Kugel auf der x-Achse nur eine GEschwindigkeit von 0,606?
ist, das ein Geschwindigkeitsvektor nur dann vollständig auf einen anderen Körper übertragen werden kann, wenn es sich um einen vollkommen elastischen Stoß handelt
und die Masse
m_{\left (v \right )} des gestoßenen Körpers der Ruhemasse
m_0 des stoßenden Körpers entspricht. Da aber laut deinem Beispiel beide Körper eine gleich große Ruhemasse besitzen, ist die dynamische Masse
m_{\left (v \right )} des gestoßenen Körpers, da er einen Geschwindigkeitsvektor aufweist, größer als die Ruhemasse
m_0 . Eben deshalb kann, obwohl der Impuls vollständig übertragen wird, der Geschwindigkeitsvektor nicht vollständig übertragen werden.
Nun nochmals zu deiner Aussage u
y müsste in der Gleichung durch u'
y ersetzt werden. Welchen Betrag hat denn u'
y in deinem GE?
In deinem Beispiel kann überhaupt kein u'
y [/latex] oder u'
x eingesetzt werden, weil die Beträge 0c aufweisen würden. Wenn du da anderer Ansicht bist, frage ich dich mal direkt:
Welchen Geschwindigkeitsvektor weist Kugel 2 in deinem GE aus Sicht von Kugel 2 auf?
mojorisin schrieb am 15.03.2018:Ist es nicht und deine Aussage gilt auch schon klassisch nicht. Dazu die einfachste Beispielrechnung zum Stoß anhand des 1D nichtrelativistischen Stoßes:
Das hat aber weder etwas mit meinem noch mit deinem GE zu tun. Es macht einen unterschied ob ein bewegter Körper parallel zur Bewegungsrichtung, oder senkrecht zur Bewegungsrichtung einen Impuls erhält. Wenn du eine Lösung suchst, dann schau dir lieber die in deinem Link an:
Sonderfall 2: Körper 1 hat eine wesentlich kleinere Masse als Körper 2; Körper 2
Schau dir mal den markierten Teil an und berücksichtige, dass wir es mit relativistischen Geschwindigkeiten zu tun haben:
v_{1,nach}= \frac {m_{0,1}} {m_{\left (v \right ),2}} \cdot v_1 = \frac {1kg} {1{,}155kg} \cdot 0{,}7c = 0{,}606c
Vergleiche es mal mit der Gleichung auf Seite 207 auf die du dich berufst :
w_x=v_1 \cdot \sqrt {1- \frac {v_2^2} {c^2}}= 0{,}7c \cdot \sqrt {1- \left ( \frac {0{,}5c} {1c} \right )^2}=0{,}606c
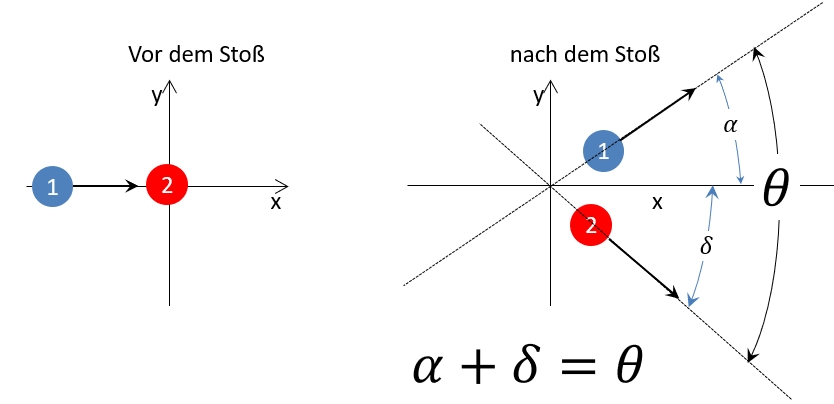
Warum du der Ansicht bist das der Geschwindigkeitsvektor auf der x-Achse vollständig übertragen wird, auf der y-Achse jedoch nicht (siehe deine Berechnungen zu Fall 2), bleibt wohl dein Geheimnis. Allerdings solltest du da langsam mal eine Erklärung für liefern, denn ohne bleibt der Widerspruch bestehen und deine Ansicht damit haltlos. Oder glaubst du die Naturgesetze richten sich nach unserer Definition des Koordinatensystems? Wohl kaum oder.
Aber genau das ist bei dir und neP der Fall. Versucht man aus euren Darstellungen eine physikalische Gesetzmäßigkeit abzuleiten, gelangt man dazu, dass eure physikalische Gesetzmäßigkeit von der Achse eines gewählten Koordinatensystems abhängt. Wird bei euch erst auf der x-Achse beschleunigt und dann auf der y-Achse, wird der Impuls auf der y-Achse nicht vollständig in Geschwindigkeit umgesetzt. Wird erst auf der y-Achse beschleunigt und dann auf der x-Achse, wird der Impuls auf der x-Achse jedoch vollständig in Geschwindigkeit umgesetzt, und der Geschwindigkeitsvektor auf der y-Achse verringert sich. Der neP leistet sich dazu sogar noch einen Spruch:
nocheinPoet schrieb am 05.03.2018:Nun komme ich dann mal zu dem zweiten "Fall", welcher sich von der Szenerie physikalisch in keiner Weise von dem ersten unterscheidet.
Ihr beide scheint nicht zu bemerken, dass diese Aussage nur auf meine Darstellung zutrifft. Denn bei mir ist nur die Reihenfolge der Impulsübertragung entscheidend, vollkommen unabhängig von einem frei wählbaren Koordinatensystem durch Menschen. Bei euch ist das eben nicht der Fall. Also, erkläre mal warum Impulse bei euch zu unterschiedlichen Wirkungen führen:
Die Zahlen 1 und 2 geben die Reihenfolge der Impulsübertragung an. Die rote Linie ist die resultierende der Geschwindigkeitsvektoren.
Wie man sieht spielt bei eurer Darstellung die Reihenfolge der Impulsübertragung keine Rolle, führt aber zu unterschiedlichen physikalischen Auswirkungen, so als wäre die x-Achse etwas Besonderes.
Bei meiner Darstellung ist die physikalische Auswirkung der Impulsübertragung nur von der Masse m
(v) des Körpers abhängig. Koordinatensysteme, die ohnehin frei gewählt werden können, haben bei mir keinen Einfluss auf die physikalische Gesetzmäßigkeit.
Statt unzählige PDF’s zu durchstöbern, in der Hoffnung das du irgendein Formalismus entdeckst den ich nicht verstehe und gleichzeitig deine Darstellung untermauern könnte, solltest du dir lieber Gedanken machen wie du den hier aufgezeigten Widerspruch entkräften möchtest, wenn du schon die anderen hartnäckig ignorierst.
pluss schrieb:Gut, du zeigst hier einen groben Lösungsweg auf, aber keine wirkliche Lösung deiner Aufgabe.
