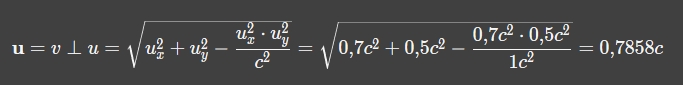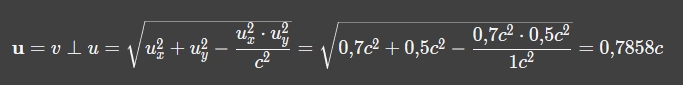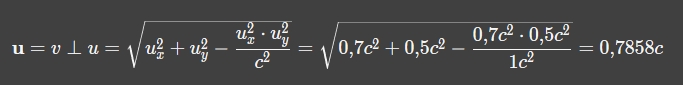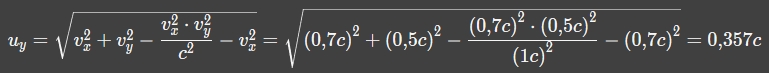Schwierigkeit der Längenkontraktion

@pluss

pluss schrieb:Verstehe ich nicht, könntest du es näher erklären?

Ich weiß nicht ob ich noch deutlicher werden kann als hier:

mojorisin schrieb:Für dieselbe Variable uy (bzw ux unten) hast du unterschiedliche Werte:

Vielleicht so: In deinen GLeichung ist einmal u^y = 0,707c und einemal u^y = 0,357c. AUßerdem ist die Variable u^y gleichzeitigg eine gegebene und gesuchte Variable, wobei die Werte derselben Variable letzendlich unterschiedlich sind. Das ist vieles aber sicherlich keine richtiige Mathemaatik.

mojorisin schrieb: In deinen GLeichung ist einmal uy = 0,707c und einemal uy = 0,357c.

Nein, wo steht das?
In Fall 1 lautet der Betrag für u_y 0,357c, und in Fall 2 0,5c.

Also erkläre doch bitte einmal näher wie du auf u_y=0,707c kommst?

mojorisin schrieb:AUßerdem ist die Variable uy gleichzeitigg eine gegebene und gesuchte Variable

Auch das solltest du mal näher erläutern. Warum sollte es sich bei u_y um eine variable handeln.
In Fall 1 beschleunigt Bob die Kugel auf der y-Achse durch einen Impulsübertrag mit 0,5773kgc.
Nach Adam Riese führt das zu einer Geschwindigkeit von 0,5c:


Ist das etwa deiner Ansicht nach falsch?

@pluss

pluss schrieb:Nein, wo steht das?

Hier! Hier steht das. Du setzt für u_y^2 = 0,5 c^2 ein. Das steht genauso da ud bedeutet: Du setzt für u_y = 0,707 c ein. (Wenn du für u_y = 0,5c einsetzen wolltest müsstest du schreiben: u_y^2 = 0,5^2c^2 oder alternativ: u_y^2 = (0,5c)^2))

Im zweiten Schritt berechnest du dann u_y hier:



Das hat eigentlich gar nichts mit dem GE zu tun sondern sind ganz grundsätzliche mathematische Fehler.

Ach so, jetzt verstehe ich dich. Ich hätte die Beträge in Klammern setzen sollen und in Latex so formatieren müssen:




Gut, mit der Kritik hast du selbstverständlich recht. Nun habe ich den Flüchtigkeitsfehler entfernt, passen die Beträge und Ergebnisse nun deiner Ansicht nach?

@pluss

pluss schrieb: Ich hätte die Beträge in Klammern setzen sollen und in Latex so formatieren müssen:

Ja, das ist grundlegend sonst ist due GLeichung eine andere.

pluss schrieb:Nun habe ich den Flüchtigkeitsfehler entfernt

Das istg kein Flüchtigkeitsfehler, sondern bedeutet eine andere Geschwindigkeit und anderes Ergebnis. Jemand der es nachrechnet weiß ja nicht das das ja "nur" falsch geschrieben ist

pluss schrieb: passen die Beträge und Ergebnisse nun deiner Ansicht nach?

Nein der Hauptkritikpunkt bleibt, ich versuch ihn dir mal noch ander zu erklären.

DU berechnest im 2. Schritt u_y = 0,357 c. WIeso setzt du dann im ersten Schritt u_y = 0,5c wenn doch u_y = 0,375c ist?

mojorisin schrieb:Das istg kein Flüchtigkeitsfehler, sondern bedeutet eine andere Geschwindigkeit und anderes Ergebnis. Jemand der es nachrechnet weiß ja nicht das das ja "nur" falsch geschrieben ist

Doch, es ist ein Flüchtigkeitsfehler. Ich wage auch zu bezweifel das der nicht erkannt wird da ja u_x^2 unmissverständlich ist, und daraufhin keiner 0{,}7c \cdot 1c^2 rechnen würde, wenn er denn mehr als nur über rudimentäre Kenntnisse der SRT verfügt. Aber wie gesagt, habe deine Kritik angenommen und damit sollte die Unstimmigkeit beseitigt sein.

mojorisin schrieb:DU berechnest im 2. Schritt uy = 0,357 c. WIeso setzt du dann im ersten Schritt uy = 0,5c wenn doch uy = 0,375c ist?

Ja, aus gutem Grund:

pluss schrieb:In Fall 1 beschleunigt Bob die Kugel auf der y-Achse durch einen Impulsübertrag mit 0,5773kgc.
Nach Adam Riese führt das zu einer Geschwindigkeit von 0,5c:

v= \frac {c} {\sqrt {1+ \frac {m_0^2 \cdot c^2} {p^2} } }= \frac {1c} {\sqrt {1+ \left ({ \frac {1kg \cdot 1c} {0{,}5773kg \cdot c} }\right )^2} }=0{,}5c

​


Ist das etwa deiner Ansicht nach falsch?

@pluss

pluss schrieb:Ja, aus gutem Grund:

Das bedeutet:
u_y = 0,5c = 0,357c

Macht nicht arg viel Sinn, oder?

pluss schrieb:In Fall 1 beschleunigt Bob die Kugel auf der y-Achse durch einen Impulsübertrag mit 0,5773kgc.
Nach Adam Riese führt das zu einer Geschwindigkeit von 0,5c:

D.h. mit dem ersten u_y meinst du eigentlich u'_y?

mojorisin schrieb:Das bedeutet:
u_y = 0,5c = 0,357c

Nein, das bedeutet es nicht. Dort steht u_y=0,5c und u'_y=0,357c.

mojorisin schrieb:D.h. mit dem ersten uy meinst du eigentlich u'_y?

Nein. Mit u_y ist auch u_y gemeint und mit u'_y ist auch u'_y gemeint.

Es geht um die generelle Aussage welche Geschwindigkeit die Kugel, wenn sie ruht, bei einem Impulsübertrag in Richtung der y-Achse von 0,5773kgc erreicht. Da du meine Frage nicht beantwortet hast, frage ich dich jetzt welche Geschwindigkeit das deiner Ansicht nach wäre?

Wenn du da schon auf ein anderes Ergebnis kommen solltest, macht es wenig Sinn über Fall 1 und 2 zu diskutieren. Dann sollten wir zunächst erst einmal hier Klarheit schaffen.

@pluss

pluss schrieb:Nein, das bedeutet es nicht. Dort steht uy=0,5c und u'y=0,357c.

Ich bitte dich genau zu lesen was ich schreibe.

In der 1. Rechung stellst du auf:


In dieser Formel gilt: u_y = 0,5c. (Also in der nun korrigierten Fassung u_y^2 = 0,5^2c^2 )

In der 2. Rechung berechnest du u_y (obwohl du in der 1. Gleichung eigentlich schon einen Wert für u_y einsetzt):



In dieser Formel gilt: u_y = 0,357c.


Nun ich denke es sollte klar sein das gilt: u_y = u_y. Dies ergbit laut deinen Rechungen: 0,5 = 0,357c.

Wenn es dir jetzt noch nicht klar ist das irgendwo etas schief läuft kann ich dir nicht mehr weiterhelfen. Klarer kann ich mich nicht mehr ausdrücken.

mojorisin schrieb:In der 2. Rechung berechnest du u_y (obwohl du in der 1. Gleichung eigentlich schon einen Wert für u_y einsetzt):

Ist dir die 1. Gleichung bekannt?
Weißt du worum es sich bei dieser Gleichung handelt?

Und wärst du bitte so freundlich statt immer neue Fragen zu stellen, auch mal die von mir gestellte zu beantworten?

pluss schrieb:Ist das etwa deiner Ansicht nach falsch?

pluss schrieb:Es geht um die generelle Aussage welche Geschwindigkeit die Kugel, wenn sie ruht, bei einem Impulsübertrag in Richtung der y-Achse von 0,5773kgc erreicht. Da du meine Frage nicht beantwortet hast, frage ich dich jetzt welche Geschwindigkeit das deiner Ansicht nach wäre?

@pluss

pluss schrieb:Ist dir die 1. Gleichung bekannt?
Weißt du worum es sich bei dieser Gleichung handelt?

Ja, tut aber nichts zur Sache. Wenn du für eine Variable zwei unterschiedlich Zahlenwerte hast ist was falsch. Entweder ALice mist u_y = 0,357c oder sie misst u_y = 0,5 c. Beides gleichzeitag aber wohl kaum.

pluss schrieb:Und wärst du bitte so freundlich statt immer neue Fragen zu stellen, auch mal die von mir gestellte zu beantworten?

Kein Whataboutism. Du berufst dich in deiner Argumentation auf Mathematik udn deine Gleichungen, wenn die aber falsch sind sind auch dein Argumente dahin. ALso klären wir zuerst diese Sache.

mojorisin schrieb:Ja, tut aber nichts zur Sache.

Eben doch, es macht vielleicht im Betrag kein Unterschied ob man relativistisch u_y+u_x oder u_x+u_y rechnet, aber es handelt sich immer noch um eine vektorielle Größe - und die Richtung des resultierenden Vektors ist abhängig davon, ob man u_y+u_x oder eben u_x+u_y gerechnet hat. Was sich dann eben in der 2. Gleichung bemerkbar macht und, wenn es nicht richtig verstanden wird, eben zu solchen Fehlschlüssen führt:

mojorisin schrieb:Entweder ALice mist uy = 0,357c oder sie misst uy = 0,5 c.

mojorisin schrieb:Du berufst dich in deiner Argumentation auf Mathematik udn deine Gleichungen, wenn die aber falsch sind

Frage ich bei dir nach ob du eine Gleichung für Falsch hältst, bekomme ich keine Antwort von dir, sondern das vorgehalten:

mojorisin schrieb:Kein Whataboutism.

Was soll daran bitte schön unsachlich sein?
Du kannst meine Berechnung nicht nachvollziehen, um zu erfahren warum, kannst du mir schlecht verbieten Fragen zu stellen.
Du solltest es auch in Betracht ziehen, dass die Ursache deines nicht nachvollziehen könnens nicht ausschließlich bei mir, sondern möglicherweise auch bei dir zu suchen ist.

mojorisin schrieb:ALso klären wir zuerst diese Sache.

Wir sollten mit einer Klärung da beginnen, wo du etwas nicht mehr nachvollziehen kannst. Das scheint meiner Ansicht nach schon bei der 1. Gleichung der Fall zu sein.
Um da Gewissheit zu haben Frage ich dich, ist die Gleichung und das Ergebnis deiner Ansicht nach so korrekt:

pluss schrieb:

\mathbf u=v \perp u=\sqrt{u_x^2+ u_y^2 - \frac {u_x^2 \cdot u_y^2} {c^2} }=\sqrt{\left ({0{,}7c} \right )^2+ \left ({0{,}5c}\right )^2 - \frac {\left ({0{,}7c}\right )^2 \cdot \left ({0{,}5c}\right )^2} {\left ({1c}\right )^2} }=0{,}7858c

@pluss

pluss schrieb:Um da Gewissheit zu haben Frage ich dich, ist die Gleichung und das Ergebnis deiner Ansicht nach so korrekt:

Mir deucht das u_y eigentlich u'_y heißen müsste und u_x eigentlich v heißen müsste welches das für den Relativgeschwindigkeitsvektor zwischen den Systemen steht,

pluss schrieb:Eben doch, es macht vielleicht im Betrag kein Unterschied ob man relativistisch uy+ux oder ux+uy rechnet

Mir geht es darum das du bei der Berchung desseleben Sachverhaltes aus demselben Inertialsystem für u_y unterschiedliche WErte hast.
Zuerst setzt du u_y = 0,5c ein dann berechnest du u_y = 0,357c.

Was ist nun u_y? 0,5c oder 0,357c? Beides geht ja wohl nicht oider? Die Kugel kann aus Sicht von ALice nur eine y-Geschwindigkeit haben. Sollte ja wohl klar sein.

Aber vielleicht hilft es ja weiter wenn du einfach mal sagst wo du die erste Fomel her hast. Ich denke du hast da einen Indexfehler drinne.

mojorisin schrieb:Mir deucht das uy eigentlich u'y heißen müsste und ux eigentlich v heißen müsste

Nein, u_y ist u_y und u_x ist u_x, ein v (Relativgeschwindigkeit) gibt es in der Gleichung nicht und wird es auch nie geben können. Wäre ja vollkommen sinnfrei.

mojorisin schrieb:Mir geht es darum das du bei der Berchung desseleben Sachverhaltes aus demselben Inertialsystem für uy unterschiedliche WErte hast.
Zuerst setzt du uy = 0,5c ein dann berechnest du uy = 0,357c.

Ich hätte die Gleichung 1. und 2. auch zusammenfassen können:

oder

Dann würde sich deine Frage erübrigen oder?

mojorisin schrieb:Aber vielleicht hilft es ja weiter wenn du einfach mal sagst wo du die erste Fomel her hast. Ich denke du hast da einen Indexfehler drinne.

Nein, nochmals überprüft, kein Index- oder sonstiger Fehler vorhanden.
Wo und warum vermutest du einen Indexfehler?
Siehst du hier auch einen Indexfehler oder ein v für Relativgeschwindigkeit?

Sicherlich nicht oder.

P.S.:

mojorisin schrieb:wo du die erste Fomel her hast

"Spezielle Relativitätsthorie", 5. Auflage, Seite 33-34, U. E. Schröder, Verlag Europa-Lehrmittel, ISBN: 978-3-8085-5649-8

@pluss

pluss schrieb:Nein eben nicht, dein permanentes widerholen [sic !] von u_y = u'_y \cdot \gamma^{-1} ist keine nachvollziehbare Berechnung, ...

Doch Du, das ist eine recht einfache Berechnung und die ist nachvollziehbar, @mojorisin der eben auch Deine Rechnung nachvollzogen hat und Dir da ganz schnell Fehler aufgezeigt hat, wird mir sicher zustimmen und meine Berechnung als eine nachvollziehbare Berechnung bezeichnen. Ganz sicher wird er nicht wie Du behaupten, sie wäre nicht nachvollziehbar.

So, halten wir mal wieder fest, Du gibst nicht vor, was nicht nachvollziehbar ist, Du kannst aber gerne erklären, Du kannst die Rechnung nicht nachvollziehen. Das würde wohl Dir hier jeder glauben und könnte es verstehen.

pluss schrieb:... denn sie beinhaltet ja immer eine Annahme von dir, nämlich den Betrag von u'_y.

Das ist keine Annahme, das ist eine Vorgabe und ergibt sich auch so aus GE und dem Relativitätsprinzip. Ich zitiere mal was:

pluss schrieb am 02.07.2017:Würde man nun noch zur Zeitmessung die Schiffsuhr von John Harrison, oder meine vorgeschlagene Uhr

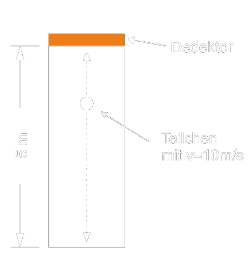
heranziehen, ergeben sich keine (signifikanten) Gangunterschiede zwischen den Uhren bewegter und ruhender Beobachter.

So, damit wir das alleine mal festgehalten haben, wieder einmal, auch da gibst Du die oder eine Geschwindigkeit der Kugel auf der y-Achse vor, und die befindet sich in Deiner "Kugeluhr" welche Du "wem" mitgeben willst. Und "wer" ist, wie wir später erfahren also Bob.

Da schon gibst Du selber eine Geschwindigkeit der Kugel auf der y-Achse im Ruhesystem S' von Bob explizit vor, dort noch mit 10 m/s ist aber egal. Du gibst da eine Geschwindigkeit vor. Und Du behauptest weiter, diese Uhr würde bewegt nicht anders gehen, als eine ruhende Uhr.

Bedeutet, in einem System S, in dem die Uhr bewegt ist, sollte die Geschwindigkeit auch mit 10 m/s gemessen werden und das unabhängig von der Geschwindigkeit zwischen dem System S und S'.

Und noch was, da schreibst Du nichts über Beschleunigung oder eine Reihenfolge einer Beschleunigung und auch nicht ein Wort über einen Impuls. Der ganze Käse kommt erst viel später von Dir und auch nur, weil Du wohl mit dem einfachen Beispiel nicht mehr genug tricksen konntest und es darum unnötig komplizierter gemacht hast.

---

So, dann mal eine klare Aussage von mir im Rahmen der Physik und der SRT:

nocheinPoet schrieb am 03.07.2017:Wie schon mehrfach erklärt, egal welche Uhr Du nimmst, sie muss lokal im Ruhesystem des Beobachters die Dauer der Sekunde für diesen richtig anzeigen, sonst geht sie falsch. Bauen also Alice und Bob jeder so eine Uhr, die für sie die Sekunde lokal richtig misst, wird diese für jeden zur Uhr bewegten Beobachter langsamer laufen.

Und genau das beschreibt die Zeitdilatation im Rahmen der SRT richtig, so kann man es auch überall nachlesen. Gilt für alle Uhren, egal ob mechanisch oder nicht, egal ob mit Kugel oder nicht, egal wann gestartet. Und Du widersprichst dieser Aussage:

pluss schrieb am 03.07.2017:Eben nicht, es hängt ausschließlich davon ab wie "Zeit" während einer Messung definiert war.

So, und damit liegst Du einfach falsch, Du widersprichst damit der SRT. Du magst das nicht einsehen und machst da nun seit über einen halben Jahr einen Tanz, denn Du immer komplexer gemacht hast, aber an der eigentlichen Tatsache kannst Du nichts ändern. Meine Aussage steht im Einklang mit der SRT, ist über 100 Jahre anerkannte Physik und Du widersprichst dem. Mainstream und anerkannte Physik muss man Dir und keinem anderen belegen, wer behauptet, so wie Du, die wäre falsch, muss hingegen seine Behauptung belegen.

Und das kannst Du natürlich nicht, eben weil Du Unfug behauptest.

Nur um auch das mal weiter festgehalten zu haben.

---

So, dann geht es um das "Gedankenexperiment" welches erst recht schwammig von Dir formuliert und dessen Beschreibung und Szenerie sich hier dann über die Zeit immer weiter entwickelt hat. Denn Du hast es immer wieder verändert, wenn man es Dir mal klar und deutlich vorgerechnet hatte und Dir Deine Fehler aufgezeigt hatte.

---

Nun noch mal ganz grundsätzlich dazu:

pluss schrieb:dein permanentes widerholen [sic !] von u_y = u'_y \cdot \gamma^{-1} ist keine nachvollziehbare Berechnung, denn sie beinhaltet ja immer eine Annahme von dir, nämlich den Betrag von u'_y.

Man kann beliebig ein System zu einem Objekt definieren, ein Ruhesystem zum Beispiel. Da kommt auch keiner, außer Dir vermutlich, der dämlich fragt, wie kann das Objekt denn da im System nur ruhen, wer hat es angehalten? So geht das ja nun gar nicht, dass ist ja nur eine Vermutung, eine Annahme, eine Behauptung, Du musst mal belegen warum das Objekt da ruhen soll, zeige mal eine Impulsrechnung dazu.

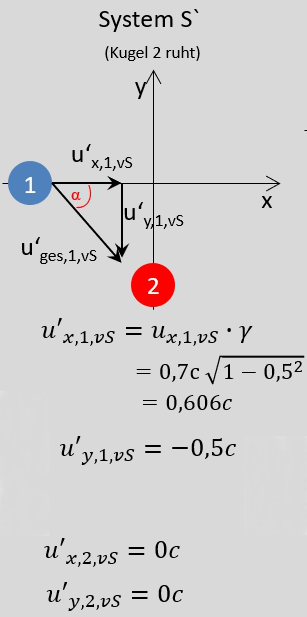
Und genau so kann man auch ein System einfach frei definieren, in dem ein Objekt, hier die Kugel eben eine beliebige Geschwindigkeit hat. Gar kein Problem, es ist eben genau das System, in dem sich eben die Kugel mit u_y = 0,5 c bewegt und auf der x-Achse eben ruht.

So, und genau das hast Du ja auch immer wieder gemacht, auch Du hast die Geschwindigkeit der Kugel einfach vorgegen.

Deine Art der "Diskussion" ist keine Diskussion mehr, es ist einfach nur frech und unverschämt was Du hier abziehst und wie Du trollst und versuchst die Leute zu verarschen.

---

Zum Rest später, auch zu Deiner Formel-Wand, @mojorisin zieht Dir ja eh dafür schon gerade die Ohren lang und den Schlüpfer über den Kopf.

nocheinPoet schrieb am 03.07.2017:Wie schon mehrfach erklärt, egal welche Uhr Du nimmst, sie muss lokal im Ruhesystem des Beobachters die Dauer der Sekunde für diesen richtig anzeigen, sonst geht sie falsch.

Ich hätte keinerlei Problem damit wenn du sagen würdest die Ur-Uhr geht falsch, da würde ich dir sogar zustimmen. Aber stattdessen versuchst du mit deiner Rhetorik die Kugel zu zwingen sich so zu verhalten wie ein Photon. Vorrechnen ist ja nicht so dein Ding, das überlässt du lieber mojorisin.

nocheinPoet schrieb:Zum Rest später, auch zu Deiner Formel-Wand

Die enthält wenigsten klare Aussagen, ist mir aus dem Grunde lieber als eine Textwand voller Behauptungen.

@pluss
Vorher:




nachher:


Plötzlich kommen ganz neue Variablen hinzu wie z.B. v_x und v_y, dafür verschwindet u_x und ein u_y. Trautrige Welt, ich verstehs nicht was das soll. Was ist falsch an gestrichenen INdexen so dass alles klar und eindeutig bleibt?

PS: In der oberen Formel subtrahiert sich v_x raus. Dann bleibt noch übrig:



Mit c² erweiteren ergibt:



Wir wissen das gilt:



Das heißt die Formel di du benutz lautet:


Kommt bekannt vor? Nur das du v_y statt u'_y schreibsts. Warum weiß leider niemand außer dir. Der Übersichtlichkeit hilft es aber sicherlich nicht. Würde man satt v_y u'_y schreiben sieht deine benutze Formel so aus:


Wieso benutzt du also nicht gleich die einfachen, üversichtlichen FOrmeln von ANfang an mit INdizierung wie wir sie schon seit Wochen benutzen?

pluss schrieb:Können wir gerne machen, dann fange doch schon mal an deine Berechnungen zu deinem Beispiel aufzuzeigen.
Ich ziehe dann selbstverständlich mit meinen nach.

Gerne, das schöne ist ja für die Frage muss man gar nicht rechnen.
Der Empfänger im Zug erhält alle Signale aller Uhren gleichzeitig, da die LG ja konstant ist. Bist du zum selben Ergebnis gekommen?

@mojorisin

mojorisin schrieb:u_y = u'_yγ ^-1 Wieso benutzt du also nicht gleich die einfachen, übersichtlichen Formeln von Anfang an mit Indizierung wie wir sie schon seit Wochen benutzen?

Weil dann jeder sofort erkennt, er rechnet genau mit der Formel, welche ich auch nehme, welche man im Rahmen der SRT eben nimmt. :D

Er hat sich doch echt so viel Mühe gegeben das zu verklausulieren, und Du hustest den Mist mal eben schnell auf den Abend weg. :D

Wie schon mehrfach gesagt, ich sehe da echt trollen und was Pathologisches.

Auch der Käse nun, man darf nicht einfach wo in einem System eine Geschwindigkeit vorgeben, wäre ja nur eine Behauptung. Und dann nun das Einführen von neuen Bezeichnungen für Variablen.

Und wie er einfach stur zu der Tatsache schweigt, dass er zu Beginn nie was über eine Beschleunigung geschrieben hat, auch da hat er nur von einer mechanischen Uhr geschrieben und seiner Kugeluhr und da auch der Kugel einfach eine Geschwindigkeit vorgegeben.

Ernsthaft, ich sehe hier wirklich trollen, auf AstroNews wäre er schon vor Monaten gesperrt worden und so richtig rund gemacht worden.

Er hat nur das Glück hier, dass es keinen Moderator gibt, der die Ahnung von Physik hat und der Bereich Wissenschaft hier von @dns nur als Bonus nebenbei läuft. In einem Physikforum würde @pluss aber so was von Kielgeholt werden ... :D

Und auch lustig, vor einigen Tagen habe ich genau diese Rechnungen hier, aber einfacher durchgeführt, ohne das Lametta, gezeigt. Einmal die Geschwindigkeit von 0,5 c im System von Bob vorgeben und ins System von Alice transformiert, kommt 0,357 c raus.

Und einmal die Geschwindigkeit von 0,5 c (immer auf der y-Achse, oben also auch) im System Alice vorgegeben und ins System von Bob transformiert, da kommt dann eben 0,7 c raus. Sind natürlich zwei unterschiedliche Szenarien.

Hat aber nichts mit einer Reihenfolge einer Beschleunigung zu tun, ja ich weiß, ist Dir alles ja klar.

Auch hatte ich die Gesamtgeschwindigkeit im System von Alice unter der Vorgabe der 0,5 c im System von Bob berechnet.

Egal wie man es macht, @pluss zeigt sich hier stur und uneinsichtig, und genau das habe ich ja prognostiziert, eben weil mir so ein Verhalten schon mehrfach aufgefallen ist. Warum auch immer, er kann da einfach nicht zurück.

​
​

mojorisin schrieb:Plötzlich kommen ganz neue Variablen hinzu wie z.B.v_x und v_y, dafür verschwindet u_x und ein u_y. Trautrige Welt

Was schreibst du ständig von Variablen?
Es gibt drei Achsen x,y,z, möchte man Geschwindigkeit addieren reicht auch eine Angabe von x, y und z. Ich kann mich aber auch deinen persönlichen wünschen anpassen. Wie hättest du es denn gerne, lieber u_y oder v_y oder etwas anderes?

Ich versuche es immer zu vermeiden Gleichungen zu kürzen. Habe erst vor kurzem ein Beispiel im Bezug von u_y zur Lorentz-Transformation gegeben. Für eine Nachvollziehbarkeit und vor allem Anwendung auch in anderen Aufgabenstellungen führen gekürzte Gleichungen zu Fehlern. Das Additionstheorem für v_x + u_y lautet nun mal:

Man kann auch schreiben:

oder

oder

Am Ergebnis ändert sich dadurch nichts.
Also was möchtest du jetzt beanstanden, das Ergebnis oder die Tatsache das ich Gleichungen nicht kürze und Indizes verwende die dir nicht "gefallen"?


Möchte nicht wissen was es für ein Theater gegeben hätte wenn ich mich über deine Berechnungen




so mokiert hätte. Deine 2 steht nicht über den Indizes, sondern daneben. Trotzdem würde keiner \left (0{,}606c \right )^2 \cdot \left (1c \right )^2 rechnen.

Dein u_{x,1,vS} \cdot \gamma ist Bullshit, es müsste u_{x,1,vS} \cdot \beta oder noch genauer u_{x,1,vS} \cdot \beta_{u_y} heißen.

Was ist \sqrt {0{,}606^2+ \left (-0{,}5 \right )^2} für eine Einheit? Äpfel, Birnen oder vielleicht doch Korinthen?
Aber wie kann aus einer knapp über dreiviertel großen Korinthe eine so große Geschwindigkeit entstehen?

Also ich habe dir nicht so überflüssige Fragen um die Ohren gehauen, einfach weil es ersichtlich ist das es sich um Flüchtigkeitsfehler handelt und klar ist um welche Einheit es sich handelt, als auch das eine Geschwindigkeit quadriert wird und nicht die Geschwindigkeit im Quadrat mit c im Quadrat multipliziert wird.

Was machen wir jetzt, wollen wir uns erst mal auf deine

mojorisin schrieb:Du berufst dich in deiner Argumentation auf Mathematik udn deine Gleichungen, wenn die aber falsch sind sind auch dein Argumente dahin

Fehler konzentrieren, auf meine, oder vielleicht das korinthenkacken in Form von Vorwürfen bleiben lassen. Wenn etwas unklar ist, kann man doch auch einfach freundlich nachfragen: Hat sich da ein Flüchtigkeitsfehler eingeschlichen, oder soll das so sein?
Bei klar offensichtlichen Flüchtigkeitsfehlern wie dein u_{x,1,vS} \cdot \gamma oder meinen 0{,}7c^2 lohnt sich eine Erwähnung doch überhaupt nicht.


P.S.: Was machst du denn wenn noch die z-Achse dazu addiert werden müsste? Auch bis zur Unkenntlichkeit kürzen?


Bin für heute erst mal raus. Bis morgen dann.