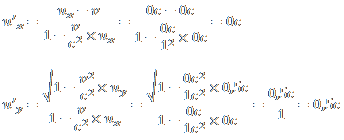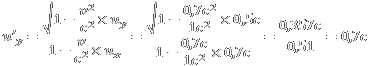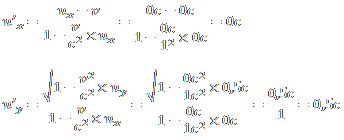Schwierigkeit der Längenkontraktion

ComCitCat schrieb:Fürs erste: Ein Objekt, dass sich in X-Richtung aus Sicht von Alice nicht bewegt, hat für Bob ne X-Geschwindigkeit. Und zwar -vx. Soweit so trivial.

mojorisin schrieb:Generell würde ich das nicht sagen. Sagen wir mal Bob bewegt sich mit 0,5c in x-Richtung und das Objekt mit 0,6c in x-RIchtung, dann wir das Objekt auch für Bob eine positive x-Geschwindigkeit besitzen

Deine Rechnung stimmt schon, aber sie trifft nicht auf meine Aussage zu, weil ich ja ausdrücklich gefordert habe das u[x]=0 (also aus Alices Sicht). Ich muss meine Aussage jetzt trotzdem zurück nehmen. Wir wollen uns ja gerade dahin tasten, dass eine y-Geschwindigkeit einen Einfluss auf die x-Komponente hat. Ein Objekt dass sich also mit genügend hoher Geschwindigkeit in y-Richtung für Alice bewegt, bei v[x]=0 soll für Bob durchaus eine von v[x] verschiedene Geschwindigkeit haben. Jetzt haben wir das Problem, dass für Bob sich also auf der X-Achse Alice und das Objekt auseinanderbewegen. Und wir müssten wenistens erklären können, wie die beiden wieder zusammen finden, wenn das Objekt auf Alice y-Achse umkehrt und zum Koordinatenursprung sprich zu Alice zurück fliegt. (Das ist jetzt der von dem Ur-Uhren-Experiment umgekehrte Fall, was aber nicht heißt das prinzipiell andere Ergebnisse rauskommen dürfen, als wir sie pluss aufgenötigt haben. ;-))

Hier muss ein Blick in deine Transformationsformeln für Geschwindigkeiten (und vielleicht Beschleunigungen) klarheit schaffen können. Wenn nicht, dann haben wir beide etwas grundlegendes nicht verstanden.

mojorisin schrieb:Das ist unmöglich, bzw wahrscheinlich nur für eine ganz bestimmte Konfiguration möglich,[...]Gibst du einen Schubs in x-Richtung ändert sich die GEschwindigkeit soweieso.
Gibst du einen Schubss orthogonal zur x-Richtung, ändert sich der RaumgGesamtgeschwindigkeitsvektor, und damit auch der Zeitvektor. Damit wird die x-GEschwindigkeit unweigerlich runtergehen.
Das einzige was gehen würde ist den orthogonalen ZUsatzimpuls, der zur Verringerung der x-GEschwindigkeit führt auszugleichen mit einer zusätzlichen BEschleunigung in x-Richtung damit dieursprünfliche Geschwindigkeit wiederhergestellt ist.

Deswegen fragte ich ja auch:

ComCitCat schrieb: in welcher Richtung Alice der Kugel (aus ihrer Sicht) einen infinitesimalen Schubs geben müsste

Mein Ansatz war jetzt der:

Wir haben den Impuls  p = mv  bzw. relativistisch = mv * Gamma

Für unser Beispiel zerlege ich den Impuls in seine x- und y- Komponente:
p = m0 * v[x] * Gamma + m0 * v[y] * Gamma
Und jetzt addiere ich einen infinitesimalen Impuls vorerst unbekannter Richtung, und fordere dann, das p[x] zwar größer wird, aber nur in dem Maße wie Gamma ansteigt (also der Massenzunahme entspricht), während sich, v[x] nicht ändert darf. Das muss ja wohl zu rechnen sein. ;-)

Deine Beschleunigungsgleichungen könnten die Antwort eventuell schon liefern. Müssen sie eigentlich. Denn wir haben ja hier ganz klar die Forderung a[x]'=0. Aber ich verstehe diese Gleichungen nicht, will sie also selber herleiten. (dafür reicht das hier aber sicherlich noch nicht aus - weil das ja nur ein Spezialfall in den Beschleunigungsgleichungen ist)

Nochmal kurz ne Frage hinterher. Ist der 3-er-Impuls in der relativistischen mechanik eigentlich überhaupt eine Erhaltungsgröße, oder müssten wir nicht eigentlich den 4er-Impuls nehmen? Und hat das einen Einfluss auf die komponentenweise Betrachtung?

@ComCitCat

nur kurz zum Rest später:

ComCitCat schrieb:Nochmal kurz ne Frage hinterher. Ist der 3-er-Impuls in der relativistischen mechanik eigentlich überhaupt eine Erhaltungsgröße,

Innerhalb eines Inertialsysstems ja. D.h. beim Stoß zweier Kugeln gilt für den 3er-Impuls p_vorher = p_nachher

Allerdings ist der 3er-Impuls nicht lorentzinvariant. D.h. bei der Transformation in ein anderes System ändern sich die Impulswerte. Lorentzinvariant ist hingegen der 4er-Impuls. Dieser ändert sich nicht beim Wechsel des Inertialsystems und ist auch eine Erhaltungsgröße.

ComCitCat schrieb:Und hat das einen Einfluss auf die komponentenweise Betrachtung?

Die einzelnen Komponenten müssen aus Sicht desselben Inertialsystems erhalten bleiben. D.h. wenn z.B. ein Kraftstoß nur auf der x-Achse wirkt muss der Impuls eines Objekts in y-Richtung derselbe bleiben da F_y = dp_y/dt = 0.

@pluss | @mojorisin | @Zotteltier

Nun wirst Du lieber @pluss wohl doch erkannt haben, dass @mojorisin und ich mit @Zotteltier einer Meinung sind und im Gleichklang der SRT schwingen, konträr eben zu dem was Du da glaubst und behauptest. Ich hatte es Dir ja vorhergesagt. Eben weil ich die Beiträge von @Zotteltier richtig lesen kann, Du glaubtest hingegen einen Widerspruch zu unseren Aussagen darin zu erkennen und ein Zuspruch zu den Deinen. War aber nicht so, hast Du ja auch schon mal bei @mojorisin so gemacht, einfach frech behauptet, seine Rechnungen würden ja Deine Behauptungen bestätigen. Da war er doch recht "überrascht".

So wird es auch bleiben, jeder der etwas Ahnung von Physik hat, und da reicht schon die 8. Klasse und ein guter Wille, wird es richtig verstehen und Deine Fehler erkennen, also sich unserer Sichtweise anschließen, der Deinen widersprechen. Die SRT ist nämlich frei von Widersprüchen und unsere Erklärungen sind es somit auch. Deine sind es nicht. Auch wenn Du diese stur ignorierst.

Du würdest hier auch nicht veralbert, wenn Du endlich zu Deinen Fehlern stehen würdest, im Gegenteil man würde es Dir wohl als Stärke zur Einsicht anrechnen. Und es könnte dann endlich mal weiter gehen. Die Physik ist nämlich spannend und mit der SRT fängt es erst an. Nur wirst Du da nie hinkommen, wenn Du da stur an Deinen Fehlern kleben bleibst.

Was ist nun mit dem "Fehlschluss" von Feynman?

---

So, ich mache mal weiter mit dem Beitrag von gestern, war damit ja noch nicht fertig. Wir erinnern uns, der gute @pluss hat eine Geschwindigkeit aus dem System S von Alice mit der LT in das System S' von Bob transformiert und wirkte dann ein wenig verwundert, dass die da dann größer war. Er sucht dann nach einer Erklärung und kam mit sehr viel Text.

Spannend ist dabei aber eben, er erklärte nicht gleich - geht nicht, ist falsch - sondern nahm das so an.

Und, wichtig, mit seiner Rechnung wollte er ja eben gerade uns hier aufzeigen, dass wir einen "Denkfehler" machen. Ich zitiere mal:

pluss schrieb am 22.10.2017:Das euer Denkfehler eben in diesem Satz steckt:

mojorisin schrieb am 20.10.2017:Wenn Bob beschleunigt, verringert sich die y-Geschwindigkeit der Kugel aus Sicht von Alice.

habe ich versucht mit dem Beispiel des Satelliten zu verdeutlichen. Brachte nur leider nichts. War wohl nicht einleuchtend genug um euren Denkfehler aufzudecken (@Zotteltier ausgenommen). Dann halt nochmals etwas abgewandelt: ...

Also, ganz deutlich erklärt er, da komme nun "etwas" das dann uns unseren "Denkfehler" aufzeigen könnte, etwas das dann ganz "einleuchtend" wäre. Man war ich gespannt ...

---

pluss schrieb am 22.10.2017:Ein Inertialsystem S, ruhend, beobachtet ein Objekt A, das sich mit einer Geschwindigkeit von 0,5 c auf der y-Achse bewegt. Ein weiterer Beobachter S', der gegenüber S ruht, beobachtet das Objekt A ebenfalls. ...

Objekt A aus Sicht von S in S'::

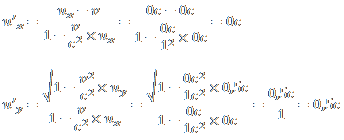
So, nun wichtig, er gibt hier die Geschwindigkeit im System S' von Bob an, die Überschrift ist natürlich falsch, muss heißen, Geschwindigkeiten in S'. Ich halte mal in bunt fest:

System S' - Ruhesystem von Bob:

u'_x = 0,0 c
u'_y = 0,5 c

Wichtig ist u'_y = 0,5 c, und bis hier passt auch noch alles.

---

Kurz nachgetragen, die Gleichung von @pluss transformiert von S nach S', bei v = 0,0 c ändert sich da natürlich nichts. Dennoch hätte er besser mal von S' nach S transformiert. Also vom System S' von Bob in das System S von Alice. Bei v = 0,0 c wäre das Ergebnis natürlich gleich, aber das wäre dann nach der Beschleunigung interessant.

Wenn dann nämlich zwischen S und S' v = 0,7 c gegeben sind, und er dann u'_y = 0,5 c von S' nach S transformiert hätte, also aus dem System von Bob in das System von Alice, dann hätte er erkannt, die Geschwindigkeit ist kleiner geworden, beträgt nun nur noch u_y = 0,357 c.

Frage ist, warum hat er das nicht auch mal getan. Warum zeigt er bei v = 0,0 c nur die Transformation von S nach S' und spart sich die Transformation bei v = 0,7 c dann ganz. Eben da wäre doch interessant gewesen, mal aus S' nach S zu transformieren.

Aber nein, da setzt er einfach u_y = u'_y gleich und transformiert dann aber u_y zurück nach S' in das System von Bob.

Hat er das bewusst so gemacht, damit nicht auffällt, dass die Geschwindigkeit kleiner wird, so wie wir es ihm die ganze Zeit erklären? Hätte er es nämlich getan, dann hätte es ihm auffallen müssen.

---

pluss schrieb am 22.10.2017:Nun wird das Objekt A und das System S' auf 0,7 c der x-Achse beschleunigt:

Objekt A aus Sicht von S:

v = 0,7 c, u_x = 0,7 c, u_y = 0,5 c

Und da ist schon der obligatorische Fehler von @pluss wieder zu sehen.

Nachdem das System S' von Bob gegenüber dem System S von Alice auf v = 0,7 c beschleunigt wurde, übernimmt er ohne Transformation die Geschwindigkeit u'_y = 0,5 c aus S' in das System S von Alice. Er behauptet also:

u_y = u'_y

Das war natürlich auch vor der Beschleunigung so noch richtig, da war die Geschwindigkeit zwischen S und S' auch v = 0,0 c. Nun ist die Situation aber eine andere, nun beträgt die Geschwindigkeit zwischen S und S' v = 0,7 c. Und darum gilt:

u_y ≠ u'_y

Richtig ist sogar:

u_y < u'_y

---

Konkret heißt das, wird eine in S gemessene Geschwindigkeit in das System S' transformiert, ist diese dort größer als in S. Und genau das hat der gute @pluss selber auch berechnet und bestätigt und belegt:



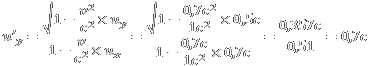
Er zeigt hier also selber:

u'_y > u_y

Offenbar erkennt er dabei nicht, dass er damit genau das bestätigt, was wir ihm hier die ganze Zeit erklären, denn das ist genau u_y < u'_y, die Geschwindigkeit der Kugel, welche Alice auf der y-Achse in ihrem System S misst, ist kleiner als die Geschwindigkeit welche Bob in seinem System S' misst.

@pluss zeigt uns hier also nicht einen Denkfehler auf unserer Seite auf, im Gegenteil bestätigt er damit genau unsere Aussagen. Eben das was wir ihm seit vielen Wochen erklären und rauf und runter rechnen.

---

Ich wiederhole mal, @pluss hat den Fehler gemacht, zu glauben, die Geschwindigkeit welche Alice für die Kugel auf der y-Achse in ihrem System S messen wird, würde sich nicht ändern, wenn das System S' mit der Kugel auf der x-Achse auf v = 0,7 c beschleunigt wird.

Er glaubt und behauptet, wenn einmal gilt:

u_y = u'_y

Dann gilt das immer. Er verkennt dabei, dass eben dieses nur in dem Fall gilt, das die Geschwindigkeit zwischen den beiden Systemen S und S' v = 0,0 c beträgt. Nur in diesem Fall ist das belegt. Er verändert nun diese Geschwindigkeit auf v = 0,7 c und postuliert dann einfach, das bleibt so, es muss weiter gelten:

u_y = u'_y (falsch wenn v ≠ 0.0 c)

Ich habe da gleich mal ein "falsch" hinter geschrieben.

---

@pluss macht also eine falsche Annahme und darum überträgt er ohne jede Transformation u'_y aus S' nach u_y in S. Er setzt:

u_y = u'_y = 0,5 c

Und dann transformiert er diese Geschwindigkeit aus S wieder zurück nach S':



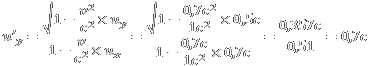
Ist seine Rechnung, ich reche es einfacher:

γ = 1,4 (der Lorentzfaktor bei 0,7 c)

u'_y = (u_y ⋅ γ) = (0,5 c ⋅ 1,4) = 0,7 c

Ergebnis ist aber gleich.

Und dann wundert er sich, dass die Geschwindigkeit nun größer geworden ist. :D

Der Fehler von @pluss liegt wieder glasklar auf dem Tisch, und wieder wird er das ignorieren, besser kann er aber kaum bestätigen, dass er darum weiß und dem nichts entgegensetzten kann. Hätte er was, würde er ganz laut tanzen.

---

Was wäre denn nun richtig gewesen?

Er hätte nachdem es eine Geschwindigkeit zwischen S und S' von v = 0,7 c gibt, die in S' gemessene Geschwindigkeit natürlich auch mit der LT in das System S von Alice transformieren müssen, und diese nicht einfach so direkt übernehmen, schauen wir uns das mal richtig an:

u_y = (u'_y ⋅ γ ^-1) = (0,5 c ⋅ 1,4 ^-1) = 0,357 c

So geht es richtig, im System S von Alice wird nach der Beschleunigung von S' auf v = 0,7 c gemessen.

Generell muss man zwischen zwei Systemen mit der LT die Geschwindigkeiten transformieren, nur wenn die Geschwindigkeit zwischen den beiden Systemen selber v = 0,0 c beträgt, dann und nur dann gilt eben:

u_y = u'_y = 0,5 c

Das liegt daran, dass der Lorentzfaktor Gamma γ dann eben 1 ist.

---

Bis hier hin erstmal, da kommt aber noch mehr, also keine Sorge, ich wollte nur noch mal den Fehler von @pluss deutlichst rausarbeiten, damit er dann weiter betroffen dazu schweigen kann. Nein, ernsthaft, es geht mir primär um die stillen Leser hier, bekomme ja weiterhin die eine oder andere Nachricht.

Was ist nun mit dem "Fehlschluss" von Feynman?

Nur mal so nebenbei, falls es jemanden interessiert. Ich habe mal die Herleitung des Gamma-Faktors aus der Lichtuhr und die Herleitung der Dilatation der Teilchenuhr aus der Lorentztransforation aufgeschrieben, und als pdf angehängt.
Dateianhang: Dilatation.pdf (215 KB)
Die Gammaherleitung ist ja bekannt aber die Herleitung für die Lichtuhr hatte ich so noch nicht gefunden.

@Zotteltier
Ich kenne die Herleitung von Gamma eigentlich nur über die Lichtuhr. Wie hast du's denn vorher gekannt?

btw mach das mit der Lichtuhr nochmal, aber lass sie diesmal umfallen (also nicht zwischen drin, dreh sie einfach um 90 grad und rechne dann nochmal). :-)
Einfach nur weil ich Leute gelesen habe, die meinten die Physik würde sofort den Bach runtergehen, wenn die Lichtuhr mal umfällt...

@ComCitCat
Hatte mich verschrieben.

Zotteltier schrieb:Die Gammaherleitung ist ja bekannt aber die Herleitung für die Lichtuhr hatte ich so noch nicht gefunden.

sollte eigentlich heißen.

"Die Gammaherleitung ist ja bekannt aber die Herleitung für die Teilchenuhr hatte ich so noch nicht gefunden."

ComCitCat schrieb:mach das mit der Lichtuhr nochmal, aber lass sie diesmal umfallen

Wenn ich sie in z-Richtung umfallen lassen darf, kann ich das gerne machen. :D

Ansonsten: Warum einfach wenns auch kompliziert geht. ;)

@Zotteltier
Wenn du eine um 90° gedrehte Lichtuhr für kompliziert hältst bist du hier ganz klar falsch...

@ComCitCat
Ich seh auch gerade, dass das nicht so wild ist. Beim Aufschreiben wirds klarer, im Kopf hatte ich mir komische Laufzeiten definiert.

@pluss | @mojorisin | @Zotteltier

So, mal zwischen durch, da ist zwar noch mehr offen, aber das hier ist zeigt noch mal zweifelsfrei auf, dass @pluss irrt und das auch erkennen können müsste, wenn er es dann wollen würde:

pluss schrieb am 22.10.2017:

Zotteltier schrieb am 22.10.2017:Gehst Du grundlegend davon aus, dass Koordinaten (Edit: insbesondere die Koordinaten Masse behafteter Teilchen) zwischen bewegten Bezugssystemen lorentz-transformiert werden müssen oder nicht?

Ja natürlich, und das unabhängig davon ob ein Objekt Ruhemasse besitzt oder nicht.

Gehen wir mal davon aus, dass er die Frage richtig verstanden hat und auch weiß, was er da als Antwort geliefert hat. Ganz deutlich erklärt er, zwischen zwei Systemen müssen Koordinaten transformiert werden.

---

---

Da haben wir die Begriffe, System, transformieren und Koordinaten. Es gibt Orts- und Zeitkoordinaten, mal ein Beispiel, die Koordinatenwerte eines Ereignisses im System S werden alle nach S' transformiert:

[x, y, z, t] ⇒ [x', y' , z', t']


Und zurück von S' nach S:

[x, y, z, t] ⇐ [x', y' , z', t']


Alle Werte werden transformiert, sie können sich alle ändern, müssen es aber nicht. Der Startpunkt der Kugel ist ein Ereignis, ebenso der Reflexionspunkt, aus beiden ergibt sich eine Strecke s und eine Zeitdauer t. Und daraus dann die Geschwindigkeit:

v = st ^-1

---

Also können Geschwindigkeiten auch immer nur in einem System angegeben werden und natürlich müssen dann auch immer alle Geschwindigkeiten transformiert werden. Geschwindigkeiten ergeben sich ja erst aus zwei Koordinaten.

u' ⇒ u; u ⇐ u'

Ich halte mal fest, @pluss hat selber erklärt, alle Koordinaten müssen mit der LT von einem in ein anderes System transformiert werden. Ohne Ausnahme, auch wenn das Objekt eine Masse besitzt, also eine Kugel und kein Photon ist.

S ⇔ S'

Wichtig, das gilt natürlich auch für alle in einem System gemessene Geschwindigkeiten.

---

---

So, der erste Teil war mit Absicht übertrieben präzise, damit er sich nicht wieder rausreden kann. Nun nehme ich wieder das letzte Beispiel von @pluss mit dem er uns hier ja unseren "Denkfehler" aufzeigen wollte:

pluss schrieb am 22.10.2017:Das euer Denkfehler eben in diesem Satz steckt:

mojorisin schrieb am 20.10.2017:Wenn Bob beschleunigt, verringert sich die y-Geschwindigkeit der Kugel aus Sicht von Alice.

habe ich versucht mit dem Beispiel des Satelliten zu verdeutlichen. Brachte nur leider nichts. War wohl nicht einleuchtend genug um euren Denkfehler aufzudecken (@Zotteltier ausgenommen). Dann halt nochmals etwas abgewandelt: ...

---

Schauen wir uns nun mal eine Geschwindigkeitstransformation von @pluss von S nach S' an.

pluss schrieb am 22.10.2017:Ein Inertialsystem S, ruhend, beobachtet ein Objekt A, das sich mit einer Geschwindigkeit von 0,5 c auf der y-Achse bewegt. Ein weiterer Beobachter S', der gegenüber S ruht, beobachtet das Objekt A ebenfalls. ...

Wichtig ist, er gibt hier die Geschwindigkeit im System S' von Bob an, die Überschrift ist natürlich falsch, muss heißen, Geschwindigkeiten in S'. Ich halte mal in bunt fest:


System S' - Ruhesystem von Bob:

u'_x = 0,0 c
u'_y = 0,5 c

Wichtig ist u'_y = 0,5 c, und bis hier passt auch noch alles. Wir wissen, Bob beobachtet in S' die Geschwindigkeit der Kugel auf der y-Achse mit:

u'_y = 0,5 c  

---

---

So, nun gibt @pluss dem System S' von Bob eine Geschwindigkeit gegenüber S:

pluss schrieb am 22.10.2017:Nun wird das Objekt A und das System S' auf 0,7 c der x-Achse beschleunigt: ...

Bevor ich jetzt die Werte von @pluss zeige, schauen wir nochmal was wir genau wissen und wirklich haben. Bob sitzt mit seiner Kugeluhr in seiner Rakete und hatte vor der Beschleunigung: u'_y = 0,5 c gemessen. Sehen wir uns dazu mal zwei andere ganz aktuelle Aussage von @pluss an:

pluss schrieb:

Zotteltier schrieb:Die 0,5 c in y-Richtung beobachtet Bob (Das ist die Vorgabe, in beiden Fällen).

Diese Vorgabe ist sinnfrei. Aus dem einfachen Grunde, weil Bob immer 0,5 c in seinem System beobachtet, unabhängig davon ob er bewegt ist oder nicht und unabhängig davon wann er die Ur-Uhr startet.

pluss schrieb:... wir wissen ja, dass Bob immer 0,5 c in seinem System messen wird.

Damit erklärt er ganz deutlich, auch nachdem nun das System S' auf v = 0,7 c gegenüber dem System S von Alice beschleunigt wurde, wird Bob darin weiter: u'_y = 0,5 c messen. Wir wissen also, auch nach der Beschleunigung von S' auf v = 0,7 c gilt:


System S' - Ruhesystem von Bob:

v = 0,7 c (Geschwindigkeit zwischen beiden Systemen)

u'_x = 0,0 c
u'_y = 0,5 c

Und @pluss bestätigt das bis hierhin mit eigenen Worten.

---

Jetzt noch mal zurück, zur ersten Aussage von ihm:

pluss schrieb am 22.10.2017:

Zotteltier schrieb am 22.10.2017:Gehst Du grundlegend davon aus, dass Koordinaten (Edit: insbesondere die Koordinaten Masse behafteter Teilchen) zwischen bewegten Bezugssystemen lorentz-transformiert werden müssen oder nicht?

Ja natürlich, und das unabhängig davon ob ein Objekt Ruhemasse besitzt oder nicht.

Damit sagt er unmissverständlich nun auch aus, dass natürlich eben die u'_y = 0,5 c aus dem Ruhesystem S' von Bob in das Ruhesystem S von Alice transformiert werden müssen. Und das mit der Lorentztransformation (LT).


Und er sagt sogar weiter:

pluss schrieb am 22.10.2017:Auch wenn man sich die eine oder andere Transformation schenken kann, und zwar dann wenn von vornherein klar ist das das Ergebnis den Wert 0 haben wird.

Wie du siehst führe ich die Transformation hier trotzdem immer durch. Einfach um aufzuzeigen das keine Widersprüche bestehen.

---

---

Sehen wir uns doch nun mal vorab an, wie diese Transformation genau ausschaut, was dabei rauskommt:


Lorentztransformation der y-Geschwindigkeit aus S' nach S:

u'_y = 0,5 c

v = 0,7 c (Geschwindigkeit zwischen beiden Systemen)

γ = (√ (1 - v²)) ^-1 = 1,4 (der Lorentzfaktor bei 0,7 c)

u_y = u'_y ⋅ γ ^-1 = 0,5 c ⋅ 1,4 ^-1 = 0,357 c


Wenn @pluss also die Geschwindigkeit u'_y = 0,5 c aus dem System S' von Bob mit der LT richtig in das System S von Alice transformiert hat, dann müsste man bei ihm das: u_y = 0,357 c finden.

Noch kurz was angefügt, wir wissen nun, Alice misst in S die Geschwindigkeit u_y = 0,357 c, natürlich können wir auch wieder zurück nach S' in das System von Bob transformieren:

u'_y = u_y ⋅ γ = 0,5 c ⋅ 1,4 = 0,5 c

Wir sehen, da passt also alles. Halten wir hier fest, wenn @pluss die Transformation richtig durchführt, muss er als Ergebnis das erhalten:

u_y = 0,357 c

---

Jetzt suchen mal bei @pluss nach der Lorentztransformation der Geschwindigkeit u'_y = 0,5 c aus dem System S' von Bob in das System S von Alice:  

pluss schrieb am 22.10.2017:Nun wird das Objekt A und das System S' auf 0,7 c der x-Achse beschleunigt:

Und da finden wir keine Transformation. Habe da den Wert u_y = 0,5 c in rot hervorgehoben. Richtig transformiert würde da aber 0,357 c stehen. Also ganz deutlich und klar, @pluss hat hier eben nicht, wie er behauptet hat, die Geschwindigkeit u'_y = 0,5 c aus dem Ruhesystem S' von Bob in das Ruhesystem S von Alice transformiert. Denn wir wissen, Bob misst in seinem System S':  

u'_y = 0,5 c

Und @pluss hatte dazu auch erklärt:

pluss schrieb am 22.10.2017:

Zotteltier schrieb am 22.10.2017:Gehst Du grundlegend davon aus, dass Koordinaten (Edit: insbesondere die Koordinaten Masse behafteter Teilchen) zwischen bewegten Bezugssystemen lorentz-transformiert werden müssen oder nicht?

Ja natürlich, und das unabhängig davon ob ein Objekt Ruhemasse besitzt oder nicht.

Und:

pluss schrieb:

Zotteltier schrieb:Die 0,5 c in y-Richtung beobachtet Bob (Das ist die Vorgabe, in beiden Fällen).

Diese Vorgabe ist sinnfrei. Aus dem einfachen Grunde, weil Bob immer 0,5 c in seinem System beobachtet, unabhängig davon ob er bewegt ist oder nicht und unabhängig davon wann er die Ur-Uhr startet.

pluss schrieb:... wir wissen ja, dass Bob immer 0,5 c in seinem System messen wird.

Richtig aus dem Ruhesystem S' von Bob in das Ruhesystem S von Alice transformiert beträgt die Geschwindigkeit der Kugel auf der y-Achse nicht:

u_y = 0,5 c

sondern:

u'_y = 0,357 c

@pluss hat definitiv nicht transformiert!

---

---

Also noch mal zusammengefasst:

1. @pluss bestätigt u'_y = 0,5 c im Ruhesystem S' von Bob.

2. @pluss erklärt, diese Geschwindigkeit wird Bob so immer in S' messen, auch wenn der sich mit seinem System selber bewegt.

3. @pluss erklärt, Geschwindigkeiten müssen immer zwischen den Systemen mit der LT transformiert werden.

4. @pluss behauptet, er würde diese Transformation immer durchführen.

5. Das Ergebnis der Transformation ist u_y = 0,357 c.

6. @pluss gibt die Geschwindigkeit für u_y mit 0,5 c an.

7. @pluss hat die Transformation nicht durchgeführt, sondern die Geschwindigkeit ohne Transformation einfach so übernommen.

8. @pluss macht damit einen entscheidenden Fehler.

---

---

Damit ist noch mal ganz deutlich der Fehler von @pluss im Detail dokumentiert und aufgezeigt, das verlangt er ja sogar immer explizit. Aber ganz sicher wird er auch dieses mal mit keinem Wort darauf eingehen, obwohl er eben dieses ja hier immer von anderen Usern verlangt.

Über drei Monate streitet er nun schon gegen die Aussagen der SRT und die Tatsachen an. Es wurde ihm immer wieder richtig erklärt, von unterschiedlichen Usern. Ihm wurden die Dinge richtig vorgerechnet, Quellen genannt, seine Fehler im Detail aufgezeigt, nichts hat gefruchtet.

Zuerst bestritt er, dass die Zeitdilatation auch für mechanische Uhren existiert. Dann kam er mit seiner Kugeluhr und dann mit Impulsen, der Reihenfolge der Beschleunigung, der Relativität der Gleichzeitigkeit, dann sollten die Systeme vor der Transformation noch hin und her gedreht werden, und dann sollte die LT auf mal nur noch für Photonen gültig sein.

Kann das alles mit Zitaten so belegen, wer dabei war, wird sich sicher erinnern. Und wenn ich eine Nebelkerze vergessen habe, bitte die Liste erweitern. @pluss ist hier von Pontius zu Pilatus gelaufen, eine Nebelkerze nach der hat er geworfen, lange Texte geschwafelt und mit unnötigen übergroßen Grafiken garniert. Dazu anderen Usern unterstellt, sie würden ja nichts vorrechnen, keine Quellen nennen, nichts belegen und stattdessen nur was behaupten.

Wenn @pluss wirklich ernsthaft daran interessiert ist, auch seine Fehler zu erkennen und die Physik richtig zu begreifen, wie er selber ja behauptet:

pluss schrieb am 22.10.2017:Ich finde es gut und richtig, dass meine Argumentation akribisch hinterfragt wird, weil nur so ein mir unentdeckt gebliebener Irrtum meiner Argumentation aufgedeckt werden kann (der einzige Grund weshalb ich mich einer Diskussion stelle).

dann ist nun aber wirklich jetzt dafür der richtige Zeitpunkt gekommen.

---

Ich gehe davon jedoch nicht aus, ich glaube dieses nicht, denn wenn wer wirklich einen ihm "unentdeckt gebliebener Irrtum" in seiner "Argumentation aufgedeckt" bekommen haben will, dann würde er ihn hier längst erkannt haben müssen. Ganz im Gegenteil ensteht hier zwangsläufig weiter der Eindruck, da soll eben nichts "aufgedeckt" werden, da will kein eigener "Irrtum" als solcher erkannt werden, da will einfach nur Recht behalten werden.

So ein Verhalten ist gegenüber allen Usern hier, die da Licht ins Dunkel tragen wollen und eben wirklich helfen, unredlich.

@Zotteltier
@mojorisin
@ComCitCat
Nicht das der Eindruck entsteht ich hätte mich aus der Affäre gezogen. Leider ist es mir aufgrund der Auftragslage momentan nicht möglich zeitnah zu antworten, werde aber noch auf eure Beiträge eingehen (spätestens Samstagabend).
Gruß Thorsten

@totte

Was los?

Ich sehe Dich schreiben, aber dann kommt doch nichts. Haue es doch nun mal klar und deutlich raus.

Und auch all die stillen Leser hier, die mir immer wieder Nachrichten schreiben, haut Eure Sichtweise nun mal offen hier in den Thread.

Besser ist das ...

@nocheinPoet
Die Forumssoftware kennt wohl kein LaTex... Ohne sind die Formeln nicht richtig darstellbar.
Gestern versucht, das Editor-Problem zu lösen...

Das war los...

@totte, benutze MS-Word oder Open-Office.
Wenn dir Latex lieber ist, dann hilft dir das vielleicht weiter:

https://www.zahlen-kern.de/editor/index.php

@totte

Ja, kenne das Problem, aber wie @pluss schon zeigte, da gibt es gewisse Lösungen für. Macht man eben ein Bild. Klar könnte man auch hier im Forum was einbinden. Aber hier verstehen nur wenige so viel von Physik, dass es wirklich anders nicht geht. Siehst Du ja ... ;)

@pluss | @mojorisin | @Zotteltier

Ich hatte ja letztens aufgezeigt und belegt, wo sich @pluss verhaut, dass er eben nicht immer richtig aus einem System in das andere transformiert. Er macht das seltsamerweise in jede Richtung und immer so, wie es ihm passt und unseren Aussagen widerspricht.

Letztes Mal übernahm er einfach die u'_y = 0,5 c, welche Bob in seinem System S' misst, in das System S von Alice ohne Transformation als u_y = 0,5 c. Von dort transformierte er dann aber genau diese Geschwindigkeit u_y = 0,5 c in das System S' von Bob zurück und wunderte sich doch ein wenig darüber, dort nun u'_y = 0,7 c zu erhalten.

@pluss macht dieses auch in die andere Richtung, wie ich gleich zeigen werde, leider sind seine Beschreibungen immer recht lang, schwülstig und wirr.

---

pluss schrieb am 24.10.2017:Alice beobachtet ein Objekt A in ihrem Bezugsystem. Das Objekt bewegt sich mit 0,5 c auf der y-Achse. Nach exakt 1 Sekunde erhält das Objekt A einen Kraftstoß, der dazu führt das das Objekt eine zusätzliche Geschwindigkeitskomponente auf der x-Achse in Höhe von 0,7 c erhält. Frage: Welche Geschwindigkeitskomponenten beobachtet Alice nun in ihrem System S?

Meine Antwort wäre: u_x = 0,7 c und u_y = 0,5 c

Wie ich sagte, echt überflüssig aufgeblasen. Es ist egal, wann da ein weiterer Kraftstoß das Objekt beschleunigt, alles für die Katz. Wenn man per Definition vorgibt, A bewegt sich mit u_x = 0,7 c auf der x-Achse im System S von Alice, braucht man doch danach nicht mehr fragen: "Und wie schnell ist nun A auf der x-Achse im System S von Alice?"

Was soll so ein Schwachsinn?


Das Lesen von so einem überflüssigen Mist kostet wirklich Lebenszeit. Das macht man einfach kurz und knapp:

---

In S bewegt sich A mit u_x = 0,7 c und u_y = 0,5 c.

---

Fertig, ist so und gut, Schulz, Punkt, Ende im Gelände. Und es braucht ganz sicher auch keine Frage, wie schnell ...

---

---

pluss schrieb am 24.10.2017:Nun wiederhole ich das obige Gedankenexperiment, allerdings wird ein zweites, auf der x-Achse mitgeführtes Bezugsystem eingeführt: Alice beobachtet ein Objekt A in ihrem Bezugsystem. Das Objekt bewegt sich mit 0,5 c auf der y-Achse. Ein weiterer Beobachter S', der im System von S ruht, beobachtet ebenfalls das Objekt A. Nach exakt 1 Sekunde erhält das Objekt A und der Beobachter S' einen Kraftstoß, der dazu führt das sowohl das Objekt als auch der Bobachter S' eine Geschwindigkeit auf der x-Achse in Höhe von 0,7 c erhalten. Frage: Welche Geschwindigkeitskomponenten beobachtet Alice nun bei Objekt A in ihrem System S?

Meine Antwort wäre: u_x = 0,7 c und u_y = 0,5 c

Meine Güte, nun wird das Ganze schon als "Gedankenexperiment" betitelt. Und wieder ist die ganze Beschreibung unnötig komplex aufgeblasen. Ich fasse es mal zusammen:

---

In S bewegt sich A mit u_x = 0,7 c und u_y = 0,5 c, so wie ein anderes System S' mit u_x = 0,7 c und u_y = 0,0 c.

---

Fertig, das ist einfach eine Vorgabe und kein "Gedankenexperiment" und darüber muss man kein Buch schreiben. Und wenn man das so vorgibt, braucht man auch nicht danach fragen, ob es denn auch so sei.

---

---

pluss schrieb am 24.10.2017:Wäre deine Antwort jetzt eine andere, nur weil ein zweites Bezugsystem definiert wurde? Ich kenne deine Antwort nicht, ich kann nur vermuten das du, aufgrund obiger Übereinstimmung, sagen würdest: Nein, das Objekt hat aus Sicht von Alice in ihrem Bezugsystem die gleichen Geschwindigkeitskomponenten wie zuvor, also: u_x = 0,7 c und u_y = 0,5 c.

Ich könnte aber genauso gut vermuten, dass du nun völlig andere Geschwindigkeitskomponenten für korrekt hältst. Nämlich dann, wenn du von S' nach S transformierst. Dann würde deine Antworten lauten müssen: u_x = 0,7 c und u_y = 0,357 c.

Welche Geschwindigkeitskomponenten sind denn nun die "richtigen" aus Sicht von Alice?

Mir unverständlich wie @pluss vermuten kann, da würde @Zotteltier nun "andere" Geschwindigkeitskomponenten für korrekt halten können. Er macht da wieder was falsch, und legt seinen Fehler dann anderen mal versuchsweise in den Mund.

Ganz sicher würde hier weder @mojorisin noch @Zotteltier auf u_y = 0,357 c kommen. Im System S sind u_y = 0,5 c per Definition vorgeben.

---

Entscheidend ist, dass @pluss schreibt:

pluss schrieb am 24.10.2017:... Ich könnte aber genauso gut vermuten, dass du nun völlig andere Geschwindigkeitskomponenten für korrekt hältst. Nämlich dann, wenn du von S' nach S transformierst. Dann würde deine Antworten lauten müssen: u_x = 0,7 c und u_y = 0,357 c.

Wieso bitte aus dem System S' in das System S?

Im zweiten, nun zusätzlichem, System S' ist die Geschwindigkeit des Objektes auf der y-Achse noch gar nicht bekannt. Die kann also gar nicht mal so eben in das System S zurück transformiert werden. Sie ist ja bisher nur im System S bekannt. Die Geschwindigkeit des Objektes auf der y-Achse im System S, war doch eben einzig nur dort per Definition vorgeben:

u_y = 0,5 c

Wenn dann müsste man erstmal die Geschwindigkeit u_y = 0,5 c in das System S' transformieren, bevor man sie von dort zurück ins System S transformieren kann.

Hier macht @pluss wieder den Fehler, Geschwindigkeiten ohne Transformation mal eben so in ein anderes System zu schieben, hier schiebt er nun die u_y = 0,5 c aus dem System S in das System S' und meint, dort würde auch u'_y = 0,5 c gemessen.

Und diese Geschwindigkeit greift er sich dann und transformiert sie zurück ins System S, kommt auf u_y = 0,357 c und wundert sich.

Ganz deutlich, er unterstellt hier @Zotteltier so darauf kommen zu können, @pluss kann sich vorstellen, dass er das so machen könnte. Ernsthaft, ich bin mir sicher, er würde das nie machen.

Das zweite System S' (ist das wo Bob immer ruht) wurde zusätzlich eingeführt, die Geschwindigkeiten des Objektes A sind bis dato aber nur im System S bekannt. Die müssen natürlich erst von dort in das System S' transformiert werden.

Ich zeige mal den richtigen Weg.

---

---

Lorentztransformation der y-Geschwindigkeit aus S nach S':

u_y = 0,5 c

v = 0,7 c (Geschwindigkeit zwischen beiden Systemen)     ⇒      γ = (√ (1 - v²)) ^-1 = 1,4 (der Lorentzfaktor bei 0,7 c)

u'_y = u_y ⋅ γ ^-1 = 0,5 c ⋅ 1,4 = 0,7 c

Im System S', dem zweiten nun zusätzlich eingeführten System bewegt sich das Objekt A mit:

u'_y = 0,7 c

auf der y-Achse. So, nun erst kann man zurück aus dem System S' in das System S transformieren.

---

Lorentztransformation der y-Geschwindigkeit aus S' zurück nach S:

u'_y = 0,5 c

v = 0,7 c (Geschwindigkeit zwischen beiden Systemen)     ⇒      γ = (√ (1 - v²)) ^-1 = 1,4 (der Lorentzfaktor bei 0,7 c)

u_y = u'_y ⋅ γ ^-1 = 0,7 c ⋅ 1,4 ^-1 = 0,5 c

Im System S, dem ersten System, bewegt sich das Objekt A natürlich auch nach der Transformation aus dem System S' zurück ins System S nicht mit u_y = 0,357 c - wie @pluss "vermutet" andere könnten das "für korrekt halten" - sondern mit:

u_y = 0,5 c

auf der y-Achse.

---

---

Man muss eben nur immer richtig transformieren und nicht wie @pluss vorab einfach Geschwindigkeiten ohne Transformation in ein anderes System schieben. Um sie dann von dort zurück zu transformieren und sich über das Ergebnis zu wundern.

Aber immerhin kann er die Rechnung selber schon richtig durchführen. Nur muss er noch lernen, es auch immer richtig zu machen. Kann ja noch besser werden ...

@pluss | @mojorisin | @Zotteltier

Ich hatte da, trotz mehrfachen Überprüfen vorab, einen kleinen Fehler durchs Kopieren in einer Rechnung, da ist ein ^-1 in einer Gleichung zuviel. Darum beide Transformationen noch einmal richtig.

---

---

Lorentztransformation der y-Geschwindigkeit aus S nach S':

u_y = 0,5 c

v = 0,7 c (Geschwindigkeit zwischen beiden Systemen)    ⇒   
γ = (√ (1 - v²)) ^-1 = 1,4 (der Lorentzfaktor bei 0,7 c)

u'_y =  u_y ⋅ γ = 0,5 c ⋅ 1,4 = 0,7 c


Im zweiten nun zusätzlich eingeführten System S', dem Ruhesystem von Bob, bewegt sich das Objekt A mit:

u'_y =  0,7 c

auf der y-Achse. So, und nun erst kann man zurück aus dem System S' von Bob in das System S von Alice transformieren.

---

Lorentztransformation der y-Geschwindigkeit aus S' zurück nach S:

u'_y = 0,5 c

v = 0,7 c (Geschwindigkeit zwischen beiden Systemen)   ⇒   
γ = (√ (1 - v²)) ^-1 = 1,4 (der Lorentzfaktor bei 0,7 c)

u_y = u'_y ⋅ γ ^-1 = 0,7 c ⋅ 1,4 ^-1 = 0,5 c


Im ersten System S, dem Ruhesystem von Alice, bewegt sich das Objekt A natürlich auch nach der Transformation aus dem System S' zurück ins System S nicht mit u_y = 0,357 c - wie @pluss "vermutet", andere könnten das "für korrekt halten" - sondern mit:

u_y = 0,5 c

auf der y-Achse.

---

---

Ich werde beide Fälle von @pluss die Tage noch mal möglichst klar und kompakt hier richtig vorrechnen.  

Moin @Zotteltier

Zotteltier schrieb am 25.10.2017:Wenn Du allerdings meinst, dass, wenn Bob u'_y=0,5c misst, auch Alice u_y=0,5c misst, ist das ein Widerspruch zur Lorentzinvarianz.

Wie kommst du darauf ich würde das meinen?

Zotteltier schrieb am 25.10.2017:    pluss schrieb:
   wir wissen ja dass Bob immer 0,5c in seinem System messen wird.

Das heißt dann aber auch, dass Alice in S immer u_y=0,357 c messen wird (so wie die Fälle hier konstruiert sind).

Erkläre mir bitte mal wie du es mit deiner Aussage in Einklang bringen möchtest:

Zotteltier schrieb am 29.09.2017:Wenn ich ein Objekt innerhalb eines gegebenen Bezugsystems betrachte, ergibt sich dann die Geschwindigkeit aus den Komponenten nach dem üblichen Vektrobetrag?
Also, da wir nur 2 dimensionen haben |u|=sqrt(ux^2+uy^2)?

(Aussage deshalb, weil du die Frage selbst mit "Ja" beantwortet hast)

Zotteltier schrieb am 24.10.2017:Ein Beobachter kann nur das messen/beobachten was in seinem Ruhesystem passiert.

Wenn Alice im System Bob nichts messen kann, können ihr auch keine Werte von S' bekannt sein. Erst wenn eine Transformation von S nach S' vollzogen wird, liegen die Werte von S‘ vor, die dann zurück nach S Transformiert werden könnten. So wie hier beschrieben:

pluss schrieb am 24.10.2017:Alice beobachtet ein Objekt A in ihrem Bezugsystem. Das Objekt bewegt sich mit 0,5c auf der y-Achse. Ein weiterer Beobachter S', der im System von S ruht, bobachtet ebenfalls das Objekt A. Nach exakt 1 Sekunde erhält das Objekt A und der Beobachter S' einen Kraftstoß, der dazu führt das sowohl das Objekt als auch der Bobachter S' eine Geschwindigkeit auf der x-Achse in Höhe von 0,7c erhalten.

Frage: Welche Geschwindigkeitskomponenten beobachtet Alice nun bei Objekt A in ihrem System S?

Warum bist du da nicht drauf eingegangen?
Weil dann der Widerspruch klar ersichtlich wird?

mojorisin schrieb am 24.10.2017:Ich habe dir zu meiner Aussage, die du Behauptung nennst, den konkreten Rechenweg samt Quellen und Diagramm vorgelegt. Wenn du darin Fehler sehen solltest, dann zeige sie bitte auf.

Wie soll ich dir Fehler aufzeigen können, wenn du deine Berechnungen nicht offenlegst?

Du hast lediglich eine Formel gepostet, nicht aber aufgezeigt wo du welche Werte eingesetzt hast. Gleiches gilt für dein Diagramm. Es kann nicht Aufgabe der User sein zu erraten welche Werte du dort eingesetzt hast.

Im Übrigen hatte ich dich darauf schon angesprochen und nachgefragt:

pluss schrieb am 10.10.2017:    mojorisin schrieb:
   Könntest du mir noch bitte ausführlich anhand der Formel erklären was du für falsch hälst?

Was für einen Betrag hast du denn als Relativgeschwindigkeit (v) angenommen? Größer 0?

Geantwortet hast du nicht.
Erzähle hier also bitte nicht deine Ergebnisse seinen für jeden nachvollziehbar wenn du zu den Werten schweigst.
Vielleicht ist dir aber auch nicht bewusst das die Beschleunigung in der SRT eine absolute und in der ART eine relativ Größe ist?[1][2]

[1] "Einführung in die Relativitätstheorie", 2. Auflage, Ray d'Inverno, Kapitel 3.7, Seite 54 von Wiley-VCH. ISBN: 978-3-527-40912-9
[2] Wikipedia: Proper reference frame (flat spacetime)

mojorisin schrieb am 23.10.2017:Also wen nich nicht so n schräges Koordinatensystem wie du zeichne dann sind die Berechungen falsch. Alles klar.

Ok, du behauptest also mein kartesisches Koordinatensystem sei "schräg", was wohl bedeuten soll "falsch", obwohl die Berechnungen auf den Formeln kartesischer Geschwindigkeitskomponenten[1] beruht.

Wie sieht denn ein deiner Ansicht nach korrektes Koordinatensystem aus, großer Meister?

Warum gibt mein "schräges" Koordinatensystem exakt das wieder, was die Formeln beschreiben?
Ist das in deinem "nicht schrägen" Koordinatensystem auch gegeben?

[1] Wikipedia: Velocity-addition formula#Standard configuration

pluss schrieb:Wie kommst du darauf ich würde das meinen?

Ich bin mir noch nicht sicher was Du genau meinst.

Einmal sagst Du Bob würde in S' immer u'_y=0,5 c messen.

In Deinen Berechnungen setzt Du aber für Alice in S u_y=0,5 c an
und berchnest dann für Bob in S' u'_y=0,7 c.

Gilt für Bob nun immer u'_y=0,5 c, oder nicht?

Aus meiner Sicht müssen die Fälle so konstruiert sein, dass in S' immer eine bestimmte Geschwindigkeit gilt, da wir ja versuchen die Frage zu klären:
"Wenn Bob seine Uhren als synchron sieht, gilt das dann auch für alle anderen Beobachter?"
Die Teilchenuhr kann für Bob aber nur mit der Lichtuhr synchron gehen wenn ganz bestimmte Geschwindigkeiten u'_y gegeben sind.

Und wenn in S' z.B. gilt u'_y=0,5c, dann gilt in S u_y=0,357 c. (für dx'=0 und v=0,7c)

Mach doch mal eine Tabelle, was in welchem Bezugssystem nach der Beschleunigung gilt, in etwa so:

	x-Komponente	y-Komponente
S	u_x=	u_y=
S'	u'_x=	u'_y=

Meinetwegen auch für die unterschiedlichen Fälle.

---

pluss schrieb:Wenn Alice im System Bob nichts messen kann, können ihr auch keine Werte von S' bekannt sein. Erst wenn eine Transformation von S nach S' vollzogen wird, liegen die Werte von S‘ vor

Genau, nur dass in unseren Fällen Bob, der in S' ruht, etwas misst, und wir von S' nach S transformieren müssen, um herauszufinden was Alice, die in S ruht, messen würde.

Das grundlegende Problem ist aus meiner Sicht, dass Du davon ausgehst:

Alice misst die Geschwindigkeit eines Objektes in y-Richtung, es findet eine Beschleunigung des Objektes in x-Richtung statt. Die vorher gemessene Geschwindigkeit in y-Richtung ist für Alice weiterhin gültig.

Das ist so schlicht falsch. Das wäre nur unter Galilei-Transformation, und damit bei kleinen Geschwindigkeiten gültig.

Sieh es mal so:
Vor der Beschleunigung ruhen S und S', und damit Alice und Bob zueinander (v=0). Beide messen u_y=u'_y=0,5 c.
Dann wird die Kugel beschleunigt.
In S' findet aber formal gar keine Beschleunigung der Kugel statt, da das Bezugssystem mitbeschleunigt wird. Deswegen misst Bob weiterhin u'_y=0,5 c.
Wenn v=/=0 ist können aber die Geschwindigkeiten u_y und u'_y nicht mehr gleich sein. Alice muss also nach der Beschleunigung eine andere Geschwindigkeit messen, nämlich die Lorentztransformierte von u'_y. Also entsprechend u_y=u'_y/gamma