Schwierigkeit der Längenkontraktion
19.11.2017 um 14:46@GuggstDu
http://www.mahag.com/neufor/viewtopic.php?f=6&t=340#p20820
Allerdings hatte Joachim noch einen Fehler entdeckt und noch eine weitere Animation hinzugefügt die allerdiongs nicht mehr abrufbar ist.
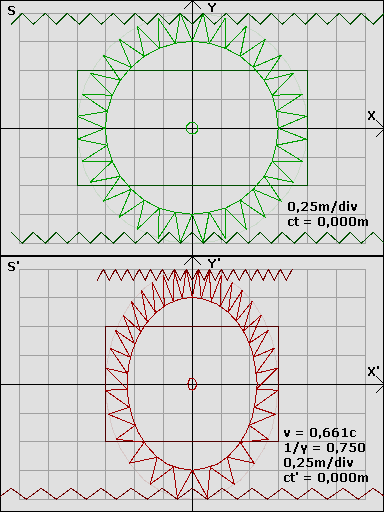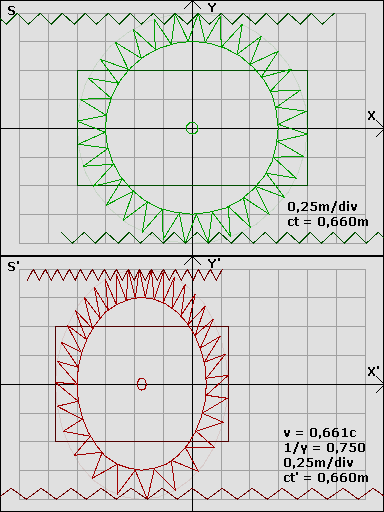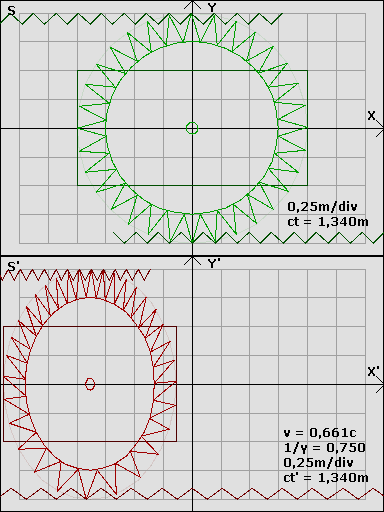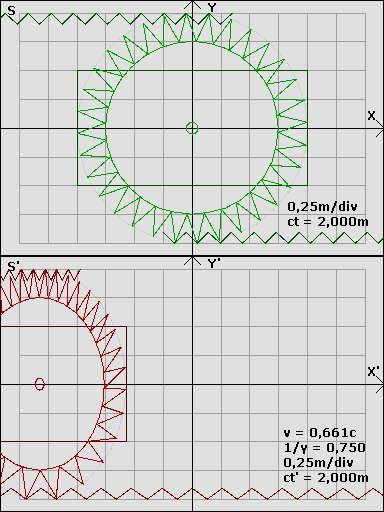
Was zeigt die Animation trotzdem? Während das obere Bild aus SIcht eines zum Rad ruhenden gemacht ist, ist das untere aus SIcht des zu einem Zahnkranz ruhenden. Dabie sieht man deutlich wie das Rad zur Ellipse gestaucht ist und trotzdem oben einehöhere Zahndicht als unten vorliegt. Das ist. z.B. völlig unintuitiv aber sehr schön veranschaulicht. Vielleicht gibt es noch mehr von Joachim SChulz und wen njemand awas findet wärs cool wenn es hier verlinkt wird.
Leider kann ich dir nicht auf die SChnelle alle Details sagen wie was auszusehen hätte, ich müsste mich dazu selbst hinsetzten und mich in das Problem einarbeiten. Aber um mal eine Vorstellung zu bekommen ist hier ein alte Grafik von Joachim Schulz:GuggstDu schrieb:Der Beobachter kann die Anzahl der Umdrehungen der Räder feststellen - sowie er die Länge der Ruhestrecke messen kann. Für ihn muss sich demnach der Umfang der Räder mit steigender Geschwindigkeit erhöhen (Radumfang = Länge der Ruhestrecke/Anzahl der Umdrehungen).
http://www.mahag.com/neufor/viewtopic.php?f=6&t=340#p20820
Allerdings hatte Joachim noch einen Fehler entdeckt und noch eine weitere Animation hinzugefügt die allerdiongs nicht mehr abrufbar ist.
Was zeigt die Animation trotzdem? Während das obere Bild aus SIcht eines zum Rad ruhenden gemacht ist, ist das untere aus SIcht des zu einem Zahnkranz ruhenden. Dabie sieht man deutlich wie das Rad zur Ellipse gestaucht ist und trotzdem oben einehöhere Zahndicht als unten vorliegt. Das ist. z.B. völlig unintuitiv aber sehr schön veranschaulicht. Vielleicht gibt es noch mehr von Joachim SChulz und wen njemand awas findet wärs cool wenn es hier verlinkt wird.





