Gedankenexperiment Lichtgeschwindigkeit RSS

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 10:04

Primpfmümpf schrieb:
Zu welchem Zeitpunkt der Jahresreise sieht der Pilot das der Stern nicht mehr leuchtet?

Das hängt davon ab, wie nah er dem Stern ist.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 10:05

Ja nach einem hlaben Jahr ist er ein halbes Lichtjahr entfehrnt @spöckenkieke

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 10:12

@Primpfmümpf
Dann ist die Frage doch ganz einfach zu beantworten. Ein halbes Jahr früher, weil das Raumschiff die halbe Strecke näher dran ist.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 10:12

genau

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 21:29

@Primpfmümpf

Primpfmümpf schrieb:
Was sieht die Raumschiffbesatzung die sich mit Lichtgeschwindingkeit in richtung diesen erloschenen Stern zu bewegt?
Zu welchem Zeitpunkt der Jahresreise sieht der Pilot das der Stern nicht mehr leuchtet?

Die Raumschiffbesatzung sieht das Erlöschen (praktisch) sofort. Denn wenn die sich mit (fast) Lichtgeschwindigkeit bewegen vergeht für die (so gut wie) keine Zeit.

Das mit "halbes Jahr" ist aber auch richtig, das gilt für das Bezugssystem Erde.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 21:34

Primpfmümpf schrieb:

Man befindet sich auf der Erde und ein Stern erlischt in einer Entfehrnung von 1 Lichtjahr. Wir sehen erst in einem Jahr diesen Stern nicht mehr

Was sieht die Raumschiffbesatzung die sich mit Lichtgeschwindingkeit in richtung diesen erloschenen Stern zu bewegt?

Zu welchem Zeitpunkt der Jahresreise sieht der Pilot das der Stern nicht mehr leuchtet?

Solche Fragen kann keiner einfach so beantworten, die müssen vorher ausgerechnet werden.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 22:10

@mindslaver

Was gibs da noch zu rechnen?

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 22:11

@Primpfmümpf

Physik besteht aus berechnen!

Ohne die Mathematik wäre die Physik undenkbar!

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 22:13

@mindslaver
Die Faktoren die es zu berechnen gilt sind aber so einfach wie 1+1 zu berechnen.

Was könnte den an dem Ergebniss des halben Jahres ab dem Raumschiffstart nicht richtig sein?

Natürlich wenn man davon ausgeht dass das Raumschiff die gleichen

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 22:26

Primpfmümpf schrieb:
Die Faktoren die es zu berechnen gilt sind aber so einfach wie 1+1 zu berechnen.

Gut, fang schon mal damit an, die nötigen Formeln für die Berechnungen aufzustellen, mit der jeder Astrophysiker etwas anfangen kann! :D Ich selbst bin leider in der Physik nicht so bewandert, aber wenn man mir anhand von Formeln, wie bsp. E(v)=mc²/√(1-v²/c²) erklärt, dass man Masse nicht auf Lichtgeschwindigkeit beschleunigen kann, da man dafür unendlich viel Energie benötige, dann komme ich noch gut mit.
Und du kannst mir ja nun auch sicherlich erklären, wie du dein Modell nun mathematisch darstellen und erklären willst.

Du siehst, wenn wir uns derartigen Geschwindigkeiten annähern, dann ist es kein "1+1" mehr, sondern dann müssen schon komplexere Formeln herhalten.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 22:34

@mindslaver

Es ging mir nur darum wenn das Raumschiff LG erreichen würde.

Und da ist die Formel v=C = (c2 + c2) x 1Lj : 2

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 22:52

Primpfmümpf schrieb:
Es ging mir nur darum wenn das Raumschiff LG erreichen würde

Dies lässt sich mathematisch nicht darstellen. Die Formel E(v)=mc²/√(1-v²/c²) ist eine Funktion, deren Graph sich asymptotisch an die Lichtgeschwindigkeit c annähert.
Wenn wir nun versuchen zu ermitteln, welcher Wert bei der Funktion herauskommt, wenn wir für v den Wert c einsetzen, also E(c)=mc²/√(1-c²/c²), so wirst du schnell erkennen, dass das Argument /√(1-c²/c²) = 0 wird, also E(v)=mc²/0. Und wie wir sicherlich beide wissen, ist ein Wert nicht durch Null teilbar. Letzen Endes heisst das nur, dass wir die Stelle c am Graphen nicht ermitteln können, was auch logisch ist, da er sich ja nur asymptotisch an c annähert, wie bereits erwähnt. So würde der Graph aussehen.

Hab leider nichts besseres gefunden! (Es ist wohl nicht der korrekte Graph zur Funktion E(v)=mc²/√(1-v²/c²), aber er stellt in etwa dar, was ich beschreiben will)

Bei diesen Bild soll c = 1 sein.


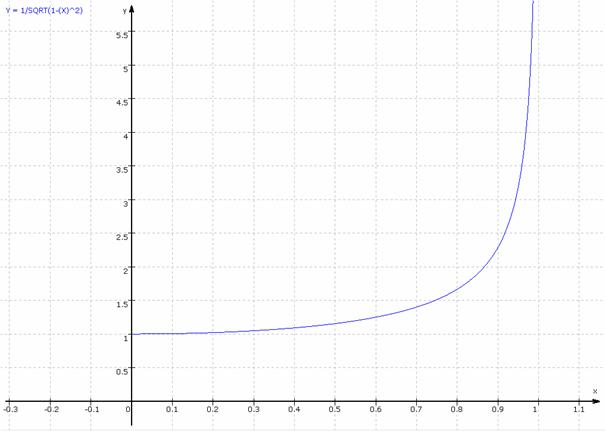
Dis ist auch der Grund, warum man sagt, es sei unmöglich, Masse auf Lichtgeschwindigkeit zu beschleunigen! ;)

Von daher können wir nicht berücksichtigen, dass das Raumschiff c fährt.

Was wir aber machen könnten, ist folgendes:

Wir könnten uns mit einem Grenzwert lim(v-->c) E(v)=mc²/√(1-v²/c²) annähern. Aber das überlasse ich anderen, wie gesagt, ich bin nicht sehr bewandert in der Mathematik.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 23:02

@mindslaver

Schau doch mal. Ich hab nocht nicht mal die Vorstellungskraft einer matematischen Wurzel. Wie soll ich da mitreden können wenn das Raumschiff r kein c betragen kann.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 23:05

@Primpfmümpf

Achso, tut mir Leid, ich wollte dich jetzt nicht erschrecken damit.

Ich mein, das war schon ein interessanter Gedankengang! :)

Allerdings muss man den erstmal berechnen, bevor man eine klare Antwort geben kann. Zudem gelten ja bei solchen Geschwindigkeiten die Zeitdillitation. Also so einfach kann man das leider auch nicht erklären.

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 23:07

@mindslaver

Ja und die lorentzkontraktion kommt dann wohl auch noch zu. Hast mich nur erschreckt dich wegen mein geringes matematisches Verständniss enttäuschen zu müssen :)

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 23:08

@Primpfmümpf

Glaub mir, meins ist auch nicht das allerbeste! :)

   Gedankenexperiment Lichtgeschwindigkeit 22.05.2012 um 23:09

Das sehe ich...






;) *scherz