@nisus:
 nisus schrieb am 01.07.2021:Wenn es jetzt so ist, daĂ laden/entladen/umladen eines Kondensators, immer die HĂ€lfte der gespeicherten Energie in den Zuleitungen verloren geht, ...
nisus schrieb am 01.07.2021:Wenn es jetzt so ist, daĂ laden/entladen/umladen eines Kondensators, immer die HĂ€lfte der gespeicherten Energie in den Zuleitungen verloren geht, ...
Das ist nicht so. Dann wĂ€ren Schwingkreise nicht sinnvoll technisch einsetzbar. Eine ganze Reihe Deiner Ăberlegungen
hier stimmen nicht. U.a. hat der Faktor 1/2 in der Formel fĂŒr die in einem Kondensator gespeicherte Energie
nichts mit dem Verlust der halben Energie beim Kondensator-Paradoxon zu tun. Dieser Faktor lĂ€sst sich auf die Formel fĂŒr das idealisierte elektrische Feld einer FlĂ€chenladung zurĂŒckfĂŒhren (E = elektrisches Feld, Q = Ladung, A = FlĂ€che, Δ
0 =
elektrische Feldkonstante):
E = \frac{1}{2}*\frac{Q}{\varepsilon_0*A}
Daraus lĂ€sst sich die Formel fĂŒr die in einem Plattenkondensator gespeicherte Energie ableiten, wobei der Faktor 1/2 erhalten bleibt. Das aber nur am Rande.
Das prinzipielle Problem beim Kondensator-Paradoxon ist, dass bei einem idealen Kondensator, der ĂŒber ideale Zuleitungen mit einer idealen Spannungsquelle verbunden ist, der Ladestrom unendlich gross wĂ€re. Das ist offensichtlich kein sinnvolles Szenario. Idealisierungen sind in der Physik ein sehr nĂŒtzliches Werkzeug, weil sie helfen, die Aufmerksamkeit von Unwesentlichem weg, und auf das Wesentliche hin zu lenken. Beim Kondensator-Paradoxon geht die Idealisierung allerdings einen Schritt zu weit. Es
muss ein strombegrenzendes Element in der Schaltung vorhanden sein, damit das Szenario Sinn ergibt. Dieses strombegrenzende Element muss aber kein Widerstand sein, es kann auch eine InduktivitĂ€t sein. In letzterem Fall geht beim Ladevorgang idealisiert keine Energie verloren, was die ErklĂ€rung dafĂŒr ist, warum bei Schwingkreisen ĂŒblicherweise relativ wenig Energie pro Schwingung verlorengeht.
Eine
InduktivitĂ€t (z.B. eine Spule) wirkt bei steigendem Stromfluss wie ein Widerstand (sie vermindert also den Stromfluss), und bei fallendem Stromfluss wie eine Stromquelle (sie verstĂ€rkt also den Stromfluss). Die entsprechende Energie wird bei steigendem Stromfluss im Magnetfeld der InduktivitĂ€t gespeichert, und bei fallendem Stromfluss von dort wieder freigesetzt. Idealisiert ist diese Zwischenspeicherung verlustfrei. Es handelt sich um das magnetische Ăquivalent zu einem Kondensator: Ein Kondensator speichert Energie in einem elektrischen Feld, eine InduktivitĂ€t speichert Energie in einem magnetischen Feld. Eine InduktivitĂ€t wirkt so, dass sie den Stromfluss genau da halten "möchte", wo er gerade ist. Solange sich der Stromfluss nicht Ă€ndert (egal, ob er gerade hoch oder niedrig ist), verhĂ€lt sich eine InduktivitĂ€t neutral, und hat nur ihren (idealisiert vernachlĂ€ssigbaren) ohmschen Widerstand.
Um die AblÀufe anhand einer Simulation zu erlÀutern, habe ich das folgende LTspice-Modell erstellt:
LTspice ist ein bekanntes, kostenloses Schaltungssimulationsprogramm, das ich sehr empfehlen kann. Die BenutzeroberflÀche ist einfach gehalten, aber gut durchdacht. Das Programm lÀsst sich
https://www.analog.com/en/design-center/design-tools-and-calculators/ltspice-simulator.html (fĂŒr Windows und Mac) frei herunterladen. Meine installierte LTspice-Version, die ich fĂŒr die Simulationen verwendet habe, ist Ă€lter als die aktuelle Version, aber ich gehe davon aus, dass die Modelle kompatibel sind.
Obwohl ich zunÀchst das klassische Kondensator-Paradoxon mit einem rein ohmschen Widerstand betrachten möchte, habe ich bereits eine InduktivitÀt in die Schaltung eingesetzt, damit ich nicht mit zwei unterschiedlichen Schaltungen hantieren muss. Die InduktivitÀt ist aber vorerst auf einen Wert von 1 Femtohenry (= 1 à 10
-15 H) gesetzt, was fĂŒr alle praktischen Belange einem Wert von Null entspricht (genau Null erlaubt LTspice nicht).
Zur Theorie des klassischen Kondensator-Paradoxons: Im Ausgangszustand ist der Kondensator C1 auf eine bestimmte Spannung U
C1(0) aufgeladen, und der Kondensator C2 vollstÀndig entladen (U
C2(0) = 0 V). Diese Spannungsdifferenz fĂŒhrt zu einem Stromfluss. Die Höhe des Stromflusses wird durch die Differenz zwischen U
C1 und U
C2, und den Wert des Widerstands R bestimmt. Da sich beim Entladen von C1 und dem Laden von C2 die Differenz zwischen U
C1 und U
C2 Àndert, Àndert sich entsprechend auch der Stromfluss. Es gilt:
\tag{1} I(t) = \frac{\Delta U(t)}{R}=\frac{U_\mathrm{C1}(t)-U_\mathrm{C2}(t)}{R}
Bei einem zeitlich konstanten Stromfluss ergibt sich die Menge an elektrischer Ladung, die wÀhrend eines bestimmten Zeitraums t durch den Stromfluss transportiert wird, gemÀss:
\tag{2} Q(t) = I*t
Bei einem zeitlich verÀnderlichen Stromfluss muss anstelle der Multiplikation integriert werden (das Grundprinzip ist dabei das gleiche, wie ich es am Anfang
dieses Beitrags erlÀutert hatte -- ein Integral ist in gewissem Sinne eine Multiplikation, bei der sich mindestens einer der Faktoren
wÀhrend der Multiplikation Àndert):
\tag{3} Q(t) = \int_0^t I(t)\,dt
Die Spannung eines Kondensators hÀngt von seiner Ladung und seiner KapazitÀt ab, wodurch sich auch die Ladung bei einer bestimmten Spannung und einer bestimmten KapazitÀt ermitteln lÀsst:
\tag{4} U = \frac{Q}{C} \quad\longrightarrow\quad Q = U*C
Die zeitabhĂ€ngige Spannung der beiden Kondensatoren ergibt sich aus ihrer jeweiligen ursprĂŒnglichen Ladung Q(0) abzĂŒglich (bei C1) oder zuzĂŒglich (bei C2) der durch den Stromfluss zwischen ihnen transportierten Ladungen:
\tag{5a} \begin{aligned}
U_\mathrm{C1}(t) &= \frac{Q_\mathrm{C1}(t)}{C} = \frac{Q_\mathrm{C1}(0)-\int_0^t I(t)\,dt}{C} = \frac{U_\mathrm{C1}(0)*C-\int_0^t I(t)\,dt}{C} \\
&= U_\mathrm{C1}(0)-\frac{1}{C}*\int_0^t \frac{U_\mathrm{C1}(t)-U_\mathrm{C2}(t)}{R}\,dt
\end{aligned}
\tag{5b} \begin{aligned}
U_\mathrm{C2}(t) &= \frac{Q_\mathrm{C2}(t)}{C} = \frac{Q_\mathrm{C2}(0)+\int_0^t I(t)\,dt}{C} = \frac{U_\mathrm{C2}(0)*C+\int_0^t I(t)\,dt}{C} \\
&= U_\mathrm{C2}(0)+\frac{1}{C}*\int_0^t \frac{U_\mathrm{C1}(t)-U_\mathrm{C2}(t)}{R}\,dt
\end{aligned}
Aufmerksamen Lesern wird nun auffallen, dass in der Formel, mit der U
C1 berechnet werden soll, U
C1 selbst vorkommt, und das auch noch unter einem Integral. Ausserdem steht unter diesem Integral auch noch U
C2, in dessen Formel das gleiche Integral nochmal vorkommt. Mit einfacher Algebra kommt man hier offensichtlich nicht weiter.
Um das Ganze etwas zu vereinfachen, wĂ€re es nĂŒtzlich, wenn sich U
C2 aus U
C1 berechnen liesse. Dazu kann man die beiden Gleichungen aufeinander addieren, wobei der Teilterm mit dem Integral aufgrund des unterschiedlichen Vorzeichens entfÀllt:
\tag{6} U_\mathrm{C1}(t) + U_\mathrm{C2}(t) = U_\mathrm{C1}(0) + U_\mathrm{C2}(0) \quad\longrightarrow\quad U_\mathrm{C2}(t) = U_\mathrm{C1}(0) + U_\mathrm{C2}(0) - U_\mathrm{C1}(t)
Die linke Gleichung besagt, dass die Summe der Spannungen zu jedem Zeitpunkt gleich der Summe der ursprĂŒnglichen Spannungen ist, was eine Folge der Konstanz der Summe der Ladungen ist.
Den gewonnenen Ausdruck fĂŒr U
C2 kann man nun in die Formel fĂŒr U
C1 einsetzen:
\tag{7} U_\mathrm{C1}(t) = U_\mathrm{C1}(0) - \frac{1}{C} * \int_0^t \frac{U_\mathrm{C1}(t)-(U_\mathrm{C1}(0) + U_\mathrm{C2}(0)-U_\mathrm{C1}(t))}{R}\,dt
Vereinfachen ergibt:
\tag{8} U_\mathrm{C1}(t) = U_\mathrm{C1}(0) - \frac{2}{R*C} * \int_0^t U_\mathrm{C1}(t)-\frac{1}{2}(U_\mathrm{C1}(0) + U_\mathrm{C2}(0))\,dt
Mit etwas Erfahrung mit dem Lösen von Differentialgleichungen sieht man, dass die gesuchte Funktion U
C1(t) vermutlich Ăhnlichkeit mit der Funktion e
x hat. FĂŒr diese Funktion gilt allgemein (siehe z.B.
hier, C ist eine beliebige Konstante):
\tag{9} e^{a*x}+C = a* \int e^{a*x}\,dx
Daraus ergibt sich (mir fehlt die Zeit, um auf die Zwischenschritte einzugehen):
\tag{10a} U_\mathrm{C1}(t) = U_\mathrm{C1}(0)-\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{2}* \left( 1-e^{-\frac{\scriptsize 2*t}{\scriptsize R*C}} \right)
FĂŒr U
C2 ergibt sich symmetrisch dazu:
\tag{10b} U_\mathrm{C2}(t) = U_\mathrm{C2}(0)+\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{2}* \left( 1-e^{-\frac{\scriptsize 2*t}{\scriptsize R*C}} \right)
Beide Spannungen nĂ€hern sich mit zunehmendem t an den Mittelwert der Anfangsspannungen an, weil sich der bei beiden Gleichungen ĂŒbereinstimmende Teilterm in der Klammer mit zunehmendem t zunehmend an 1 annĂ€hert.
Auf dieser Basis kann man nun die am Widerstand R in WĂ€rme umgewandelte Energie berechnen. FĂŒr die entsprechende Leistung gilt:
\tag{11} P_\mathrm{R}(t) = \Delta U(t)*I(t) = \Delta U(t)*\frac{\Delta U(t)}{R} = \frac{\Delta U(t)^2}{R} = \frac{(U_\mathrm{C1}(t)-U_\mathrm{C2}(t))^2}{R}
Einsetzen von U
C1 und U
C2 ergibt (einige Teilterme von U
C1 und U
C2 heben sich dabei gegeneinander auf):
\tag{12} P_\mathrm{R}(t) = \frac{\left((U_\mathrm{C1}(0)-U_\mathrm{C2}(0))*e^{-\frac{\scriptsize 2*t}{\scriptsize R*C}}\right)^2}{R}
Vereinfachen ergibt:
\tag{13} P_\mathrm{R}(t) = \frac{(U_\mathrm{C1}(0)-U_\mathrm{C2}(0))^2}{R}*e^{-\frac{\scriptsize 4*t}{\scriptsize R*C}}
Zur Ermittlung der Energie muss dieser Ausdruck ĂŒber die Zeit integriert werden:
\tag{14} W_\mathrm{R}(t) = \int_0^t P_R(t)\,dt = \int_0^t \frac{(U_\mathrm{C1}(0)-U_\mathrm{C2}(0))^2}{R}*e^{-\frac{\scriptsize 4*t}{\scriptsize R*C}}\,dt
Das unbestimmte Integral lÀsst sich ziemlich einfach lösen:
\tag{15} \int \frac{(U_\mathrm{C1}(0)-U_\mathrm{C2}(0))^2}{R}*e^{-\frac{\scriptsize 4*t}{\scriptsize R*C}}\,dt = \frac{(U_\mathrm{C1}(0)-U_\mathrm{C2}(0))^2}{R}*-\frac{R*C}{4}*e^{-\frac{\scriptsize 4*t}{\scriptsize R*C}}
Einsetzen der Integrationsgrenzen 0 und t ergibt:
\tag{16} W_\mathrm{R}(t) = \frac{(U_\mathrm{C1}(0)-U_\mathrm{C2}(0))^2*C}{4}*\left(1-e^{-\frac{\scriptsize 4*t}{\scriptsize R*C}}\right)
FĂŒr den Grenzwert fĂŒr t â â ergibt sich:
\tag{17} \lim\limits_{t\rightarrow\infty} W_\mathrm{R}(t) = \frac{(U_\mathrm{C1}(0)-U_\mathrm{C2}(0))^2*C}{4}
Der Wert des Widerstands kommt in der Formel fĂŒr den Grenzwert nicht mehr vor. Das bedeutet, dass die ingesamt am Widerstand in WĂ€rme umgewandelte Energie fĂŒr ausreichend grosse Werte von t (was in der Praxis i.d.R. bereits fĂŒr ziemlich kleine Werte < 1 s gilt) vom Widerstandswert unabhĂ€ngig, bzw. fĂŒr alle Widerstandswerte (quasi) gleich ist. FĂŒr das klassische Kondensator-Paradoxon-Szenario mit U
C2(0)=0 ergibt sich fĂŒr den Grenzwert genau die HĂ€lfte der im Kondensator C1 gespeicherten Energie, wie zu erwarten war.
Nun zur Simulation. ZunÀchst nochmal die Schaltung:

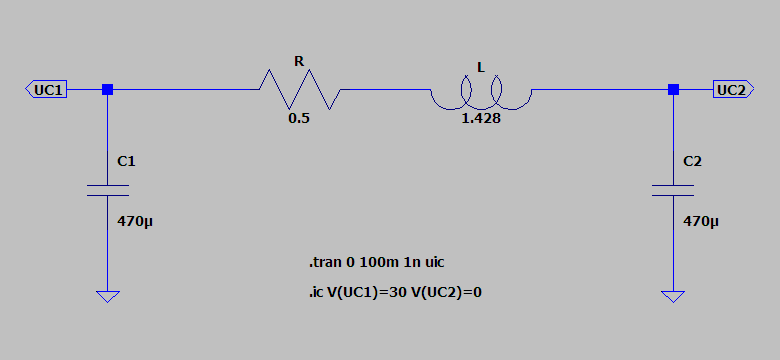
Die beiden Kondensatoren C1 und C2 haben jeweils eine KapazitĂ€t von 470 ”F. Der Widerstand R hat einen Wert von 0,5 âŠ. Die InduktivitĂ€t L ist mit einem Wert von 1 fH (= 1 Ă 10
-15 H), wie oben erlÀutert, vorerst deaktiviert (d.h. verhÀlt sich wie eine einfache Leitung). Der Kondensator C1 ist im Ausgangszustand auf eine Spannung U
C1 = 30 V aufgeladen, der Kondensator C2 ist im Ausgangszustand ungeladen, entsprechend U
C2 = 0 V. Die letzteren beiden Werte werden in der .ic-Direktive ("Initial Condition") festgelegt. Den Grund, warum ich diese spezifischen Werte verwendet habe, erlÀutere ich spÀter. Die Zeitdauer der Simulation ist in der .tran-Direktive auf 1 ms festgelegt.
Die Schaltung ist in der folgenden Textdatei gespeichert, die sich mit LTspice öffnen lÀsst:
Dateianhang: Kondensator_Paradoxon.asc (0 KB)Nicht zwingend notwendig, aber sinnvoll als ErgÀnzung ist die folgende Textdatei mit den Plot-Definitionen (darin wird festgelegt, welche Kurven auf welche Weise im Plot-Fenster angezeigt werden):
Dateianhang: Kondensator_Paradoxon.plt (0 KB)Die Plot-Definitions-Datei wird automatisch mit der Schaltung geladen, wenn sie im gleichen Verzeichnis wie die Datei mit der Schaltung gespeichert ist, und den gleichen Dateinamen (natĂŒrlich abgesehen von der Extension) hat.
Ein Simulationslauf fĂŒhrt zu folgendem Resultat:
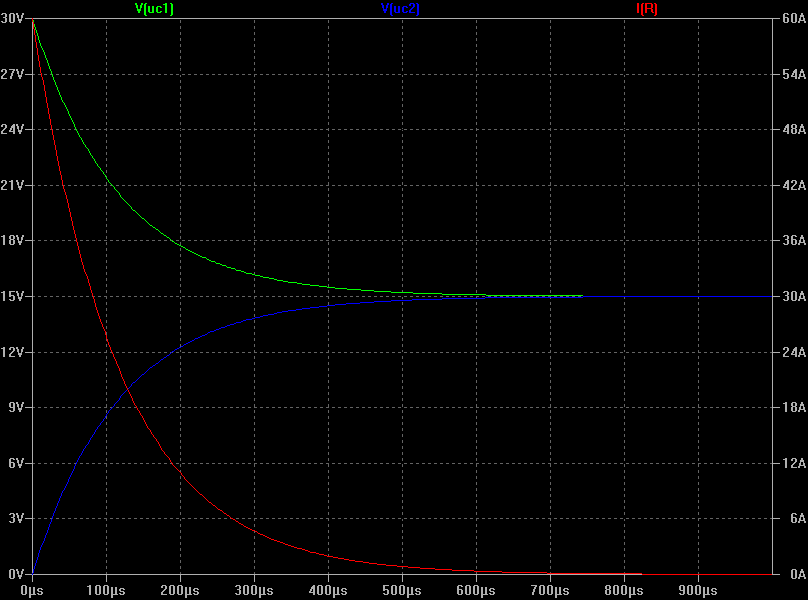
Die grĂŒne Kurve entspricht dem Verlauf von U
C1, die blaue Kurve dem Verlauf von U
C2, und die rote Kurve dem Stromfluss I zwischen den beiden Kondensatoren.
Mittels der Cursor-Funktion von LTspice lassen sich die folgenden Beispielwerte bei t â 100 ”s auslesen (der Cursor lĂ€sst sich nicht ganz exakt bei 100 ”s positionieren):
\begin{array}{rr}
U_\mathrm{C1}\mathrm{(99{,}8216\,”s):} & \mathrm{21{,}42530\,V} \\
U_\mathrm{C2}\mathrm{(99{,}8216\,”s):} & \mathrm{8{,}57471\,V} \\
I\mathrm{(99{,}8216\,”s):} & \mathrm{25{,}70120\,A} \\
\end{array}
Diese Werte kann man nun mit den Ergebnissen vergleichen, die die oben ermittelten Formeln fĂŒr U
C1 (10a), U
C2 (10b) und I (1) liefern:
\begin{alignedat}{3}\tag{18}
U_\mathrm{C1}(99{,}8216\,”s) &= \mathrm{30\,V-\frac{30\,V-0\,V}{2}* \left( 1-e^{-\frac{\scriptsize 2*99{,}8216Ă10^{-6}\,s}{\scriptsize 0{,}5\,âŠ*470Ă10^{-6}\,F}} \right) } &&â \mathrm{21{,}414138\,V} \\
U_\mathrm{C2}(99{,}8216\,”s) &= \mathrm{\hphantom{0}0\,V+\frac{30\,V-0\,V}{2}* \left( 1-e^{-\frac{\scriptsize 2*99{,}8216Ă10^{-6}\,s}{\scriptsize 0{,}5\,âŠ*470Ă10^{-6}\,F}} \right) } &&â \mathrm{\hphantom{0}8{,}585862\,V} \\
I(99{,}8216\,”s) &= \mathrm{\frac{30\,V-0\,V}{0{,}5\,âŠ}*e^{-\frac{\scriptsize 2*99{,}8216Ă10^{-6}\,s}{\scriptsize 0{,}5\,âŠ*470Ă10^{-6}\,F}}} &&â \mathrm{25{,}656553\,A}
\end{alignedat}
Die Werte stimmen halbwegs ĂŒberein, allerdings nicht allzu genau. Woran könnte das liegen? Hier zeigt sich der Unterschied zwischen einer analytischen Lösung und einer numerischen Lösung. Die oben ermittelten Formeln stellen analytische Lösungen dar. Man setzt die gewĂŒnschten Werte in die jeweilige Formel ein, und erhĂ€lt in einem Schritt das Ergebnis. Dieses Ergebnis ist im Rahmen der Genauigkeit der Eingangswerte und der verwendeten Rechengenauigkeit exakt. Eine Simulation ist hingegen (zumindest ĂŒblicherweise) eine numerische Lösung. Bei einer numerischen Lösung wird das Ergebnis in vielen kleinen Schritten berechnet, wobei jeder Schritt nur eine NĂ€herungslösung ist. I.d.R. ist das Ergebnis um so genauer, je kleiner man die Schrittweite macht (was allerdings nur bis zu einer gewissen Grenze funktioniert). Eine kleinere Schrittweite bedeutet jedoch auch, dass es lĂ€nger dauert, das Ergebnis zu berechnen, weil eine entsprechend grösserere Zahl von Schritten erforderlich ist.
Zum Vergleich fĂŒhre ich die Simulation nun noch mal mit einer kleinen Ănderung durch. Ich begrenze durch das EinfĂŒgen des zusĂ€tzlichen Werts 1n an vorletzter Position (zwischen dem bereits vorhandenen "1n" und "uic") in der folgenden Direktive den maximalen Timestep bei der Simulation auf 1 Nanosekunde (= 1 Ă 10
-9 s = eine Milliardstel Sekunde).
.tran 0 1m 1n 1n uicDie Simulation lĂ€uft nun deutlich langsamer. Ein maximaler Timestep von 1 ns bei einer Simulationszeit von 1 ms bedeutet, dass bei der Simulation mindestens 1 Million Schritte durchgefĂŒhrt werden mĂŒssen. Erneutes Auslesen der Beispielwerte ergibt:
\begin{array}{rr}
U_\mathrm{C1}\mathrm{(99{,}8216\,”s):} & \mathrm{21{,}41410\,V} \\
U_\mathrm{C2}\mathrm{(99{,}8216\,”s):} & \mathrm{8{,}58592\,V} \\
I\mathrm{(99{,}8216\,”s):} & \mathrm{25{,}65630\,A} \\
\end{array}
Die Ăbereinstimmung ist nun erheblich besser, allerdings immer noch nicht 100%ig. Es wĂ€re sicherlich möglich, durch Justieren weiterer Einstellungen (eine weitere Verkleinerung des Timesteps ist nicht unbedingt zielfĂŒhrend) der Simulation eine noch genauere Ăbereinstimmung zu erreichen, wobei sich allerdings die Frage stellt, in wie weit das einen Nutzen hat. FĂŒr die meisten praktischen Anwendungszwecke reicht die Genauigkeit, die mit den Standardeinstellungen von LTspice erreicht wird, aus. Mir ging es in diesem Fall darum, zu zeigen, was die Ursache fĂŒr die Abweichungen zwischen der Simulation und den Ergebnissen der analytisch ermittelten Formeln ist.
Nun zur Theorie des Falls mit InduktivitÀt. Die Spannungsdifferenz zwischen den beiden Kondensatoren setzt sich in diesem Fall aus der Spannungsdifferenz am Widerstand R und der Spannungsdifferenz an der InduktivitÀt L zusammen:
\tag{19} \Delta U_\mathrm{ges}(t) = \Delta U_\mathrm{R}(t)+\Delta U_\mathrm{L}(t)
Der Stromfluss I(t) durch den Widerstand R und die InduktivitÀt L ist nach dem
1. Kirchhoff'schen Gesetz gleich. FĂŒr den Widerstand (fĂŒr dessen Wert ich nun R
R statt R verwende, da R
R nicht lÀnger der Gesamtwiderstand im Stromkreis ist) gilt:
\tag{20} \Delta U_\mathrm{R}(t) = R_\mathrm{R}*I(t)
FĂŒr die InduktivitĂ€t gilt (entsprechend dem allgemeinen Zusammenhang zwischen Spannung und Strom bei
InduktivitÀten):
\tag{21} \Delta U_\mathrm{L}(t) = L*\frac{dI(t)}{dt}=L*\dot I(t)
Der Punkt ĂŒber dem I ist die in der Physik ĂŒbliche Scheibweise fĂŒr die erste Ableitung einer Funktion nach der Zeit (diese Notation geht direkt auf Newton zurĂŒck). Die Spannungsdifferenz an der InduktivitĂ€t hĂ€ngt also nicht vom aktuellen Wert des Stromflusses, sondern -- wie ich weiter oben erlĂ€utert hatte -- von dessen Ănderungsrate ab.
Um einer Formel fĂŒr den Stromfluss nĂ€her zu kommen, kann man nun Gleichung (20) nach I(t) auflösen,
\Delta U_\mathrm{R}(t) anhand von Gleichung (19) ersetzen, und anschliessend
\Delta U_\mathrm{L}(t) anhand von Gleichung (21) ersetzen:
\tag{22} I(t) = \frac{\Delta U_\mathrm{R}(t)}{R_\mathrm{R}} = \frac{\Delta U_\mathrm{ges}(t)-\Delta U_\mathrm{L}(t)}{R_\mathrm{R}} = \frac{\Delta U_\mathrm{ges}(t)-L*\dot I(t)}{R_\mathrm{R}}
Nun soll
\Delta U_\mathrm{ges}(t) durch die Differenz zwischen
U_\mathrm{C1}(t) und
U_\mathrm{C2}(t) ersetzt werden. FĂŒr die letzteren beiden Werte gilt entsprechend den Gleichungen (5a) und (5b):
\tag{23a} U_\mathrm{C1}(t) = U_\mathrm{C1}(0)-\frac{1}{C}*\int_0^t I(t)\,dt
\tag{23b} U_\mathrm{C2}(t) = U_\mathrm{C2}(0)+\frac{1}{C}*\int_0^t I(t)\,dt
Bilden der Differenz ergibt:
\tag{24} U_\mathrm{C1}(t)-U_\mathrm{C2}(t)=U_\mathrm{C1}(0)-U_\mathrm{C2}(0)-\frac{2}{C}*\int_0^t I(t)\,dt
Der Ausdruck rechts kann nun fĂŒr
\Delta U_\mathrm{ges}(t) in Gleichung (22) eingesetzt werden:
\tag{25} I(t) = \frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)-\frac{2}{C}*\int_0^t I(t)\,dt-L*\dot I(t)}{R_\mathrm{R}}
Die Gleichung enthĂ€lt nun ausser I(t) nur noch Konstanten, kann also gelöst werden. Als Lösung ergibt sich (der Lösungsweg ist ziemlich aufwĂ€ndig, und wĂŒrde hier zu weit fĂŒhren):
\tag{26} I(t)=2*\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2}}*e^{-\frac{\scriptsize R_\mathrm{R}*t}{\scriptsize 2*L}}*\sin \left( \frac{t}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} \right)
Es gibt noch eine zweite Lösung, die aber weniger interessant ist. Die zweite Lösung gilt dann, wenn der Ausdruck unter den Wurzeln negativ wird. Physikalisch bedeutet das, dass der Strom primÀr durch den Widerstand R, und nicht durch die InduktivitÀt L begrenzt wird. Das Verhalten der Schaltung ist dann Àhnlich wie im Fall ohne InduktivitÀt. Deshalb gehe ich auf die zweite Lösung hier nicht weiter ein.
Zur Berechnung der Spannungen der Kondensatoren wird das Integral des Stromflusses von 0 bis t gebraucht:
\begin{aligned}\tag{27}
\int_0^t I(t)\,dt &= C*\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{2}* \Bigg( 1-e^{-\frac{\scriptsize R_\mathrm{R}*t}{\scriptsize 2*L}}* \Bigg( \cos \Bigg( \frac{t}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} \Bigg) \\
&\hphantom{\,=\,}+\frac{1}{\sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}*\sin \Bigg( \frac{t}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} \Bigg) \Bigg) \Bigg)
\end{aligned}
FĂŒr U
C1 ergibt sich durch Einsetzen von Gleichung (27) in Gleichung (23a):
\begin{aligned}\tag{28a}
U_\mathrm{C1}(t) &= U_\mathrm{C1}(0)-\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{2}* \Bigg( 1-e^{-\frac{\scriptsize R_\mathrm{R}*t}{\scriptsize 2*L}}* \Bigg( \cos \Bigg( \frac{t}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} \Bigg) \\
&\hphantom{\,=\,}+\frac{1}{\sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}*\sin \Bigg( \frac{t}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} \Bigg) \Bigg) \Bigg)
\end{aligned}
FĂŒr U
C2 ergibt sich symmetrisch dazu (der nicht ausgeschriebene Rest stimmt mit Gleichung (28a) ĂŒberein:
\tag{28b} U_\mathrm{C2}(t) = U_\mathrm{C2}(0) + ...
Die grundsĂ€tzliche Struktur der Gleichungen fĂŒr U
C1 und U
C2 stimmt also mit dem Fall ohne InduktivitĂ€t (Gleichungen (10a) und (10b)) ĂŒberein, lediglich der Ausdruck in der Klammer ist deutlich komplizierter. Aus dem Vorhandensein der cos- und sin-Teilterme kann man schliessen, dass es zu einem Schwingungsvorgang kommt.
Nun zur Simulation. Die Schaltung stimmt weitgehend mit der vorhergehenden Schaltung ĂŒberein, lediglich die InduktivitĂ€t ist nun mit einem Wert von 500 ”H aktiv. Ausserdem ist die Zeitdauer der Simulation nun auf 10 ms festgelegt.
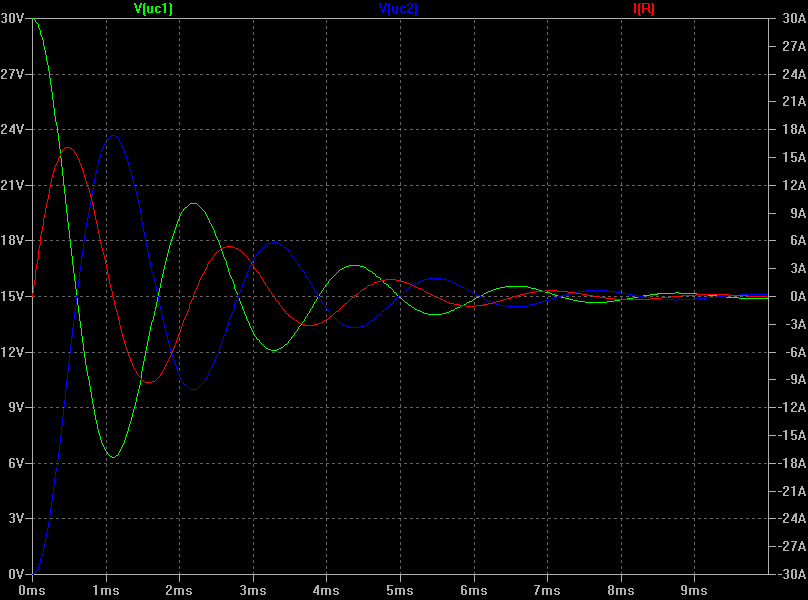
Genau wie bei der Simulation ohne InduktivitĂ€t entspricht die grĂŒne Kurve dem Verlauf von U
C1, die blaue Kurve dem Verlauf von U
C2, und die rote Kurve dem Stromfluss I zwischen den beiden Kondensatoren.
Der entscheidende Unterschied zur vorhergehenden Schaltung ist, dass C2 nun nicht mehr nur auf die HĂ€lfte (15 V) der ursprĂŒnglichen Spannung von C1 (30 V) aufgeladen wird, sondern auf ca. 79% (â 23,7 V). Entsprechend wird C1 bis auf ca. 21% (â 6,3 V) entladen. Dieser Zustand tritt nach ca. 1,1 ms ein. Sofern der Umladevorgang allerdings zu diesem Zeitpunkt nicht unterbrochen wird, kommt es zu einem umgekehrten Stromfluss. Nun wird C1 aus C2 geladen. Da bei jedem Umladevorgang ein Teil der Energie am nach wie vor vorhandenen Widerstand R in WĂ€rme umgewandelt wird, gleichen sich die Spannungen bei jeder Schwingung weiter an.
Sofern man den Stromfluss nach der ersten Halbschwingung (d.h. beim ersten Maximum von U
C2) unterbricht -- was sich z.B. durch EinfĂŒgen einer Diode in den Stromkreis erreichen lĂ€sst, die nur einen Stromfluss von C1 nach C2 zulĂ€sst -- ergibt sich fĂŒr die zu diesem Zeitpunkt (t
peak â 1,1 ms) in den Kondensatoren gespeicherte Energie:
\begin{alignedat}{2}\tag{29}
W_\mathrm{C} &= \frac{1}{2}*C*U^2 \\
W_\mathrm{C2}(t_\mathrm{peak}) &â \frac{1}{2}*C*(79\,\%*U_\mathrm{C1}(0))^2 &&â 62{,}4\,\%*W_\mathrm{C1}(0) \\
W_\mathrm{C1}(t_\mathrm{peak}) &â \frac{1}{2}*C*(21\,\%*U_\mathrm{C1}(0))^2 &&â \hphantom{0}4{,}4\,\%*W_\mathrm{C1}(0)
\end{alignedat}
Im Gegensatz zur Schaltung ohne InduktivitĂ€t ist also zu diesem Zeitpunkt in der Summe noch ca. 67%, d.h. 2/3 der ursprĂŒnglichen Energie in den Kondensatoren gespeichert. Dieser Prozentsatz lĂ€sst sich auf nahezu 100% steigern, indem man den Wert der InduktivitĂ€t L erhöht, oder den Wert des Widerstands R verringert.
Der Grund, warum eine InduktivitĂ€t dazu fĂŒhrt, dass weniger (bis nahezu gar keine) Energie am Widerstand R in WĂ€rme umgewandelt wird, beruht auf der weiter oben erlĂ€uterten, weitgehend verlustfreien Zwischenspeicherung eines Teils der durch die InduktivitĂ€t hindurchfliessenden Energie in ihrem Magnetfeld. Dadurch wird der Stromfluss zum einen gleichmĂ€ssiger (d.h. weicht weniger stark von seinem Durchschnittswert ab) und wird zum anderen ĂŒber einen lĂ€ngeren Zeitraum gestreckt (was einen niedrigeren Durchschnittswert zur Folge hat).
Dazu ein einfaches Beispiel: Ein Widerstand von 1 ⊠sei fĂŒr fĂŒr eine bestimmte Zeit von einem bestimmten Strom durchflossen. Die am Widerstand in WĂ€rme umgewandelte (und damit dem Stromkreis verlorengehende) Leistung und Energie berechnet sich allgemein gemĂ€ss:
\tag{30} P_\mathrm{R} = U*I,\;U=R*I \longrightarrow\quad P_\mathrm{R} = R*I^2
\tag{31} E_\mathrm{R} = P_\mathrm{R}*t = R*I^2*t
Bei einem Stromfluss von 10 A fĂŒr 2 s ergibt sich fĂŒr die Energie:
\tag{32a} E_\mathrm{R} = \mathrm{1\,âŠ*(10\,A)^2*2\,s} = \mathrm{200\,Ws}
Bei einem Stromfluss von 15 A fĂŒr 1 s, und einem anschliessenden Stromfluss von 5 A fĂŒr 1 s ergibt sich fĂŒr die Energie:
\tag{32b} E_\mathrm{R} = \mathrm{1\,âŠ*(15\,A)^2*1\,s+1\,âŠ*(5\,A)^2*1\,s} = \mathrm{250\,Ws}
Obwohl der Durchschnittswert der StromstĂ€rke in beiden FĂ€llen gleich ist (10 A), und der Strom insgesamt fĂŒr den gleichen Zeitraum (2 s) fliesst, wird im zweiten Fall (d.h. bei einem ungleichmĂ€ssigeren Stromfluss) deutlich mehr Energie am Widerstand in WĂ€rme umgewandelt (und geht damit dem Stromkreis verloren).
In diesem Zusammenhang wĂ€re es nĂŒtzlich, wenn sich das Maximum der von C1 auf C2 ĂŒbertragenen Energie aus einem gegebenen Parametersatz berechnen liesse. Dazu muss zunĂ€chst der Zeitpunkt t
peak bestimmt werden. Ein Blick auf den Plot zeigt, dass die Stromkurve I(t) immer genau zu den Zeitpunkten, wenn U
C2 ein Maximum (und U
C1 ein Minimum) hat, vom positiven in den negativen Bereich wechselt. Solange der Strom von C1 nach C2 fliesst, ist der Stromfluss positiv, sobald der Strom von C2 nach C1 fliesst, ist der Stromfluss negativ, und genau dazwischen Null. Daraus ergibt sich folgender Ansatz:
\tag{33} I(t_\mathrm{peak})=0 \quad\longrightarrow\quad 2*\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2}}*e^{-\frac{\scriptsize R_\mathrm{R}*t_\mathrm{peak}}{\scriptsize 2*L}}*\sin \left( \frac{t_\mathrm{peak}}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} \right) = 0
Die Gleichung rechts ist zum einen fĂŒr t â â erfĂŒllt, was jedoch keine nĂŒtzliche Lösung fĂŒr das gestellte Problem ist. Ansonsten ist die Gleichung immer dann erfĂŒllt, wenn das Argument der Sinus-Funktion (der Teilterm in der Klammer) ein Vielfaches von Ï (im
BogenmaĂ, entsprechend 180° im GradmaĂ) betrĂ€gt, da:
\sin(n*Ï)=0,\, n \in \Z. FĂŒr den gesuchten ersten Nulldurchgang von I(t) fĂŒr t > 0 ergibt sich:
\tag{34} \frac{t_\mathrm{peak}}{2*L}*\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2} = 1*Ï \quad\longrightarrow\quad t_\mathrm{peak} = \frac{2*L*Ï}{\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2}}
Einsetzen der bei der Simulation verwendeten Werte ergibt:
\tag{35} t_\mathrm{peak} = \mathrm{\frac{2*500Ă10^{-6}\,H*Ï}{\sqrt{\frac{8*500Ă10^{-6}\,H}{470Ă10^{-6}\,F}-(0{,}5\,âŠ)^2}}} â \mathrm{1{,}093\,ms}
Der Wert stimmt mit der Simulation ĂŒberein.
Mit der Formel fĂŒr t
peak kann man nun die Spannung U
C2 zu diesem Zeitpunkt berechnen. Die Argumente der Cosinus- und der Sinus-Funktion kĂŒrzen sich dabei so, dass als Wert jeweils Ï ĂŒbrig bleibt:
\begin{aligned}\tag{36}
U_\mathrm{C2_{\scriptsize max}} =U_\mathrm{C2}(t_\mathrm{peak}) &= U_\mathrm{C2}(0)+\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{2} \\
&\hphantom{\,=\,}* \left( 1-e^{-\frac{\small Ï}{\small \sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}}* \left( \cos(Ï)+\frac{1}{\sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}*\sin(Ï) \right) \right)
\end{aligned}
Aufgrund von
\cos(Ï)=-1 und
\sin(Ï)=0 ergibt sich daraus:
\tag{37} U_\mathrm{C2_{\scriptsize max}} = U_\mathrm{C2}(0)+\frac{U_\mathrm{C1}(0)-U_\mathrm{C2}(0)}{2}* \left( 1+e^{-\frac{\small Ï}{\small \sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}} \right)
Einsetzen der bei der Simulation verwendeten Werte ergibt:
\tag{38} U_\mathrm{C2_{\scriptsize max}} = \mathrm{0\,V+\frac{30\,V-0\,V}{2}* \left( 1+e^{-\frac{\small Ï}{\small \sqrt{\frac{8*500Ă10^{-6}\,H}{(0{,}5\,âŠ)^2*470Ă10^{-6}\,F}-1}}} \right)} â \mathrm{23{,}684\,V}
Als Berechnungs-Link (unterstĂŒtzt nur den Fall U
C2(0)=0):
U_\mathrm{C2_{\scriptsize max}} â(U/2)*(1+e^-(Ï/(â((8*L)/(R^2*C)-1)))) where U=30, R=0.5, C=470*10^-6, L=500*10^-6Auch dieser Wert stimmt mit der Simulation ĂŒberein.
Mit Gleichung (37) lÀsst sich also bei einem gegebenen Parametersatz vorausberechnen, auf welche Spannung C2 maximal aufgeladen wird. Dabei gilt allerdings die Bedingung, dass der Ausdruck unter der Wurzel positiv sein muss. Ist das nicht der Fall, wird der Strom primÀr durch den Widerstand R, und nicht durch die InduktivitÀt L begrenzt, was zur Folge hat, dass C2 -- wie im Fall ohne InduktivitÀt -- maximal auf den Mittelwert der Anfangsspannungen von C1 und C2 aufgeladen wird.
Bisher habe ich alle analytischen Berechnungen so durchgefĂŒhrt, dass auch von Null abweichende (ĂŒbrigens auch negative) Anfangsspannungen U
C2(0) fĂŒr C2 zulĂ€ssig sind. Um den Aufwand etwas zu verringern, fĂŒhre ich die folgenden Berechnungen nur fĂŒr den Fall U
C2(0)=0 durch.
Der Anteil (von 0..1) der Energie, die maximal von C1 nach C2 ĂŒbertragen wird, berechnet sich gemĂ€ss:
\tag{39} f_\mathrm{\tiny W} = \frac{W_\mathrm{C2_{\scriptsize max}}}{W_\mathrm{C1}(0)} = \frac{\frac{1}{2}*C*(U_\mathrm{C2_{\scriptsize max}})^2}{\frac{1}{2}*C*(U_\mathrm{C1}(0))^2} = \left( \frac{U_\mathrm{C2_{\scriptsize max}}}{U_\mathrm{C1}(0)} \right) ^2
Einsetzen von Gleichung (37) (mit U
C2(0)=0) in Gleichung (39) ergibt:
\tag{40} f_\mathrm{\tiny W} = \left( \frac{\dfrac{U_\mathrm{C1}(0)}{2}* \left( 1+e^{-\frac{\small Ï}{\small \sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}} \right)}{U_\mathrm{C1}(0)}\right) ^2 = \frac{1}{4}*\left( 1+e^{-\frac{\small Ï}{\small \sqrt{\frac{8*L}{R_\mathrm{R}^2*C}-1}}} \right)^2
Einsetzen der bei der Simulation verwendeten Werte ergibt:
\tag{41} f_\mathrm{\tiny W} = \mathrm{\frac{1}{4}* \left( 1+e^{-\frac{\small Ï}{\small \sqrt{\frac{8*500Ă10^{-6}\,H}{(0{,}5\,âŠ)^2*470Ă10^{-6}\,F}-1}}} \right)^2} â \mathrm{0{,}623} = \mathrm{62{,}3\,\%}
Als Berechnungs-Link:
f_\mathrm{\tiny W} â(1/4)*(1+e^-(Ï/(â((8*L)/(R^2*C)-1))))^2 where R=0.5, C=470*10^-6, L=500*10^-6Auch dieser Wert stimmt mit der Simulation ĂŒberein. Der kleine Unterschied zu Gleichung (29) ist rundungsbedingt.
Durch Auflösen von Gleichung (40) nach L kann man zu einem ansonsten gegebenen Parametersatz und einem gewĂŒnschten Anteil f
W der EnergieĂŒbertragung von C1 nach C2 den erforderlichen Wert der InduktivitĂ€t L berechnen (wobei die Formel nur fĂŒr Werte von f
W im Bereich von 0,25 < f
W < 1 gĂŒltig ist):
\tag{42} L = \frac{C*R_\mathrm{R}^2}{8}* \left( \frac{Ï^2}{\ln^2(2*\sqrt{f_\mathrm{\tiny W}}-1)}+1 \right)
Testen mit den Werten der Simulation ergibt:
\tag{43} L â \mathrm{\frac{470Ă10^{-6}\,F*(0{,}5\,âŠ)^2}{8}* \left( \frac{Ï^2}{\ln^2(2*\sqrt{0{,}623}-1)}+1 \right)} â \mathrm{0{,}0004989\,H} = \mathrm{498{,}9\,”H}
Als Berechnungs-Link:
L â(C*R^2)/8*(Ï^2/(ln^2(2*â(f)-1))+1) where R=0.5, C=470*10^-6, f=0.623Das stimmt im Rahmen der Rundungsgenauigkeit mit dem Wert 500 ”H in der Simulation ĂŒberein.
Nun kann man z.B. den Wert der InduktivitĂ€t berechnen, der erforderlich ist, um 99% der Energie von C1 nach C2 zu ĂŒbertragen:
L_{99\%} â(C*R^2)/8*(Ï^2/(ln^2(2*â(f)-1))+1) where R=0.5, C=470*10^-6, f=0.99 â 1,428 H
Das ist ein bemerkenswert hoher Wert. Eine InduktivitĂ€t dieser Grösse wĂŒrde man in der Praxis kaum fĂŒr einen solchen Zweck einsetzen. Der hohe Wert ist im wesentlichen darauf zurĂŒckzufĂŒhren, dass der erforderliche Wert der InduktivitĂ€t sehr stark ansteigt, je dichter der Anteil der ĂŒbertragenen Energie bei 100% liegen soll. Gibt man sich z.B. mit 98% statt 99% zufrieden, genĂŒgt eine wesentlich kleinere InduktivitĂ€t:
L_{98\%} â(C*R^2)/8*(Ï^2/(ln^2(2*â(f)-1))+1) where R=0.5, C=470*10^-6, f=0.98 â 0,352 H
Nun eine Simulation mit dem analytisch ermittelten Wert der InduktivitĂ€t 1,428 H fĂŒr 99% EnergieĂŒbertragung von C1 nach C2:
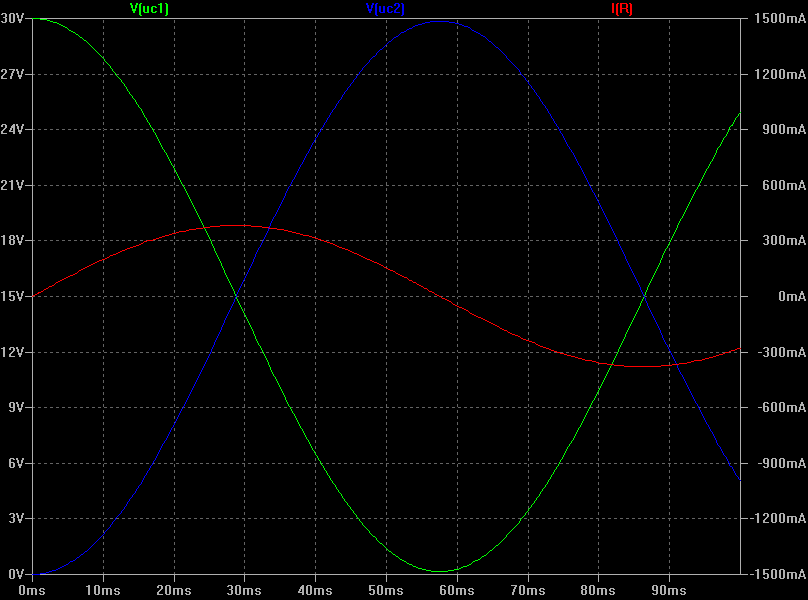
Genau wie bei den vorhergehenden Simulationen entspricht die grĂŒne Kurve dem Verlauf von U
C1, die blaue Kurve dem Verlauf von U
C2, und die rote Kurve dem Stromfluss I zwischen den beiden Kondensatoren.
Im Plot lĂ€sst sich mittels der Cursor-Funktion von LTspice eine maximale Spannung von ca. 29,85 V fĂŒr C2 auslesen. Dieser Wert wird nach ca. 57,55 ms erreicht.
FĂŒr den Anteil der ĂŒbertragenen Energie ergibt sich:
\tag{44} f_\mathrm{\tiny W} = \frac{W_\mathrm{C2_{\scriptsize max}}}{W_\mathrm{C1}(0)} = \frac{\frac{1}{2}*C*(U_\mathrm{C2_{\scriptsize max}})^2}{\frac{1}{2}*C*(U_\mathrm{C1}(0))^2} = \left( \frac{U_\mathrm{C2_{\scriptsize max}}}{U_\mathrm{C1}(0)}\right) ^2 â \left( \mathrm{\frac{29{,}85\,V}{30\,V}} \right) ^2 â 0{,}99
Der Wert stimmt mit dem analytisch ermittelten Wert ĂŒberein.
Nun kann man noch den Zeitpunkt des Maximums von U
C2 in der Simulation mit dem analytisch ermittelten Wert (entsprechend Gleichung (34)) vergleichen:
\tag{45} t_\mathrm{peak} = \frac{2*L*Ï}{\sqrt{\frac{8*L}{C}-R_\mathrm{R}^2}} â \mathrm{\frac{2*1{,}428\,H*Ï}{\sqrt{\frac{8*1{,}428\,H}{470Ă10^{-6}\,F}-(0{,}5\,âŠ)^2}}} â \mathrm{0{,}05755\,s} = \mathrm{57{,}55\,ms}
Als Berechnungs-Link:
t_\mathrm{peak} =(2*L*Ï)/(â((8*L)/C-R^2)) where R=0.5, C=470*10^-6, L=1.428Auch hier stimmt der Wert in der Simulation mit dem analytisch ermittelten Wert ĂŒberein.
Am Rande noch zu einem weiteren Effekt, der bei der Schaltung mit InduktivitĂ€t dann relevant wird, wenn Schwingungen auftreten (d.h. nicht mittels einer Diode oder auf anderem Wege unterbunden werden), und der Wert des ohmschen Widerstands der Schaltung sehr gering ist: Es kommt zur Abstrahlung elektromagnetischer Wellen, was mit einem zusĂ€tzlichen Energieverlust verbunden ist. Die entsprechenden Berechnungen sind ziemlich aufwĂ€ndig, weshalb ich an dieser Stelle dazu nur auf ein Paper von Prof. Kirk T. McDonald (m.E. der weltweit fĂŒhrende Experte fĂŒr klassische Elektrodynamik) verweisen möchte:
A Capacitor Paradox (pdf) (Archiv-Version vom 15.06.2021)
Abschliessend zum Grund, warum ich die spezifischen Werte U
C1(0) = 30 V, R = 0,5 âŠ, C = 470 ”F und L = 500 ”H in der Simulation verwendet habe. Vor einigen Jahren hat jemand bei physicsforums.com Messungen an einem realen Versuchsaufbau mit diesen Werten durchgefĂŒhrt:
Capacitors paradox #28. Der Wert fĂŒr den Widerstand R wird dabei allerdings nicht explizit genannt, weshalb ich einen geeigneten glatten Wert auf Basis der Messwerte geschĂ€tzt habe. Deshalb ist die Ăbereinstimmung nur ungefĂ€hr, zeigt aber, dass das Verhalten der Schaltung auch in der RealitĂ€t im wesentlichen mit den analytischen Berechnungen und der Simulation ĂŒbereinstimmt.
Die Schaltung bei physicsforums.com enthĂ€lt beim ersten Versuch eine zusĂ€tzliche Diode, die dazu fĂŒhrt, dass nur ein Stromfluss von C1 nach C2 möglich ist. Der Stromfluss endet daher, nachdem U
C2 den Maximalwert erreicht hat.
nisus schrieb:Wenn es jetzt so ist, daĂ laden/entladen/umladen







