mathematics schrieb:sorry das ich nicht geblieben bin wo der Pfeffer wächst (mach ich jetzt aber, also keine Panik). Darfst dir nun also im gewohnter Weise auf die Schulter klopfen.
Den Pfeffer findeste übrigens hier:
SRT Wechselseitige Zeitdilatation in zwei zueinander bewegten Systemen Dort findeste auch die Schulterklopfer, etwa diesen hier:
der optische Dopplereffekt wird mit der SRT erklärt, ist also relativistisch, nur der akustische Dopplereffekt kann klassisch mit Newton erklärt werden. Nur damit es hier nicht wen irritiert. ;)
Ich denke, derjenige, den es irritieren würde, wird diesen Hinweis nicht würdigen wollen ... ;)
Daß ich dies bestätigt habe, mehrfach, immer wieder, weils nicht ankam, ging zumindest an dem Auctor des zweiten Zitats bis heut vorbei.
mathematics schrieb:Ich habe das jetzt mal ausgerechnet (was du nach wie vor nicht geschafft hast)
Was ich nach wie vor nicht
vorgehabt habe. Was Du freilich hättest wissen können, da ich dies bereits mitgeteilt habe.
Schließlich reicht schon allein das Wissen um das Zwillingsparadoxon völlig aus, um sich klar zu machen, daß von Start bis Landung die Uhr auf der Erde weit häufiger getickt haben muß als die Uhr im Raumschiff, daß also der Raumfahrer während seiner gesamten Reise weit mehr Signale von der Erde empfangen hat, als er an die Erde abgab. Da hilft auch kein Rausrechnen des Dopplereffekts, zu irgendeinem Zeitraum muß der Raumfahrer die irdischen Signale der für ihn bewegt wahrgenommenen Erde häufiger ankommen wahrgenommen haben alsdie von ihm erdwärts geschickten Signale losgehen. Geht gar nicht anders.
mathematics schrieb:Damit ist das für mich abgeschlossen, aber auch Allmy.
Zumindest hast Du Dich nicht abgemeldet. Darum schreib ich noch, vor allem das jetzt:
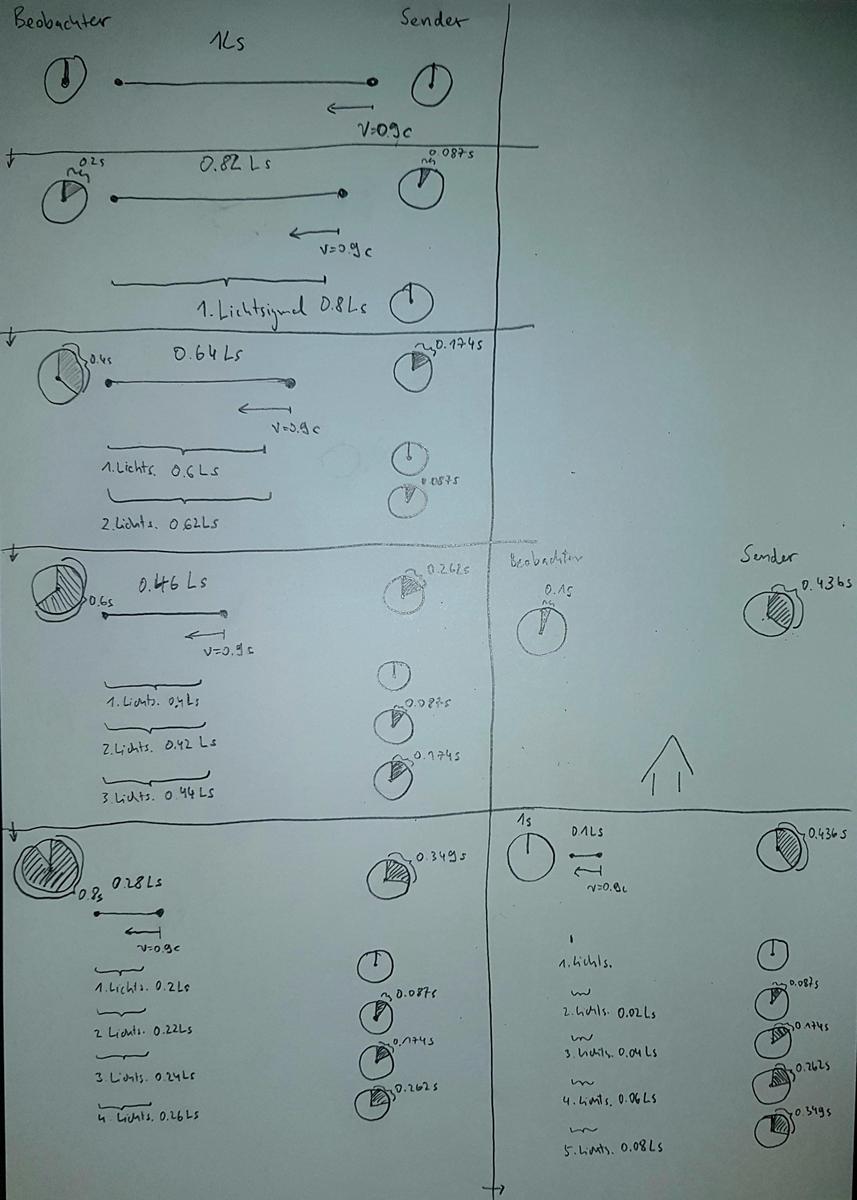
mathematics schrieb:Im konkreten Beispiel, s. Bild, bewegt sich ein 'Sender' auf einen 'Beobachter' in einer Entfernung von einer Lichtsekunde mit 0.9 c auf den Beobachter zu. Nach einer Sekunde kommen die ersten Photonen der Uhr an und innerhalb einer Zeitspanne von 0.1 s auf der Uhr des Beobachters verstreichen 'scheinbar' (trotz bewegter Uhr) 0.436 s auf der Uhr des Senders.
Prima, das ist der Dopplereffekt. Rechnet der Beobachter diesen nun noch heraus (sofern das empfangene Licht von der Uhr über Spektrallinien verfügt), wird er feststellen, daß die 5 Lichtsignale nicht innerhalb von 0,1[Periode] Sekunden abgegeben wurden, sondern innerhalb von 1,1[Periode] Sekunden. Damit ist übrigens gewährleistet, daß die bewegte Uhr des Raumfahrers für den unbewegten Beobachter auf der Erde langsamer tickt. Denn in den ermittelten 1,1 Sekunden hat der Erdbeobachter an den Raumfahrer nicht nur fünf, sondern ganze zwölf Lichtsignale an den Raumfahrer gesandt.
Jetzt dreh aber mal den Spieß um. er Raumfahrer sieht nicht erst im letzten Zehntel seiner 0,436 Sekunden nen Lichtsignal einer sich auf ihn mit 0,9c zubewegenden Erde, sondern die ganzen 0,436 Sekunden über. Und empfängt in dieser Zeit 22 dieser Signale statt nur 5 wie die, welche er abgesandt hat. Würde er nun den Dopplereffekt herausrechnen, so würde die Erde sich aus 3,924 Lichtsekunden Entfernung auf ihn zubewegen, dafür 4,36 Sekunden benötigen, aber vergangen wären für die Erde aus Sicht des Raumfahrers mindestens 2,1 und höchstens weniger als 2,2 Sekunden. Deutlich weniger als seine ermittelten 4,36 Sekunden. Auch er also sieht die bewegte Uhr nach herausrechnen des Dopplereffektes langsamer ticken als die seine.
Das wolltet Ihr mir ja erklären.Das ist aber eben nur die halbe Miete. Denn so läßt sich das Zwillingsparadoxon nicht erklären.
Nehmen wir ein Raumschiff an, das an der Erde vorbeifliegt, und zwar so dicht, daß ein außen angebrachter Sensor einen auf der Erde angebrachten Sensor beührt. Die Berührung dient dem Start sowohl der Uhr auf dem Raumschiff als auch der Uhr auf der Erde. Beide ticken ab dem Sensorkontakt und senden dem je anderen alle Zehntelsekunde ein Signal. Das Raumschiff fliegt ohne Beschleunigung oder Abbremsen weiter (ignorieren wir hier mal die Abbremsung des Raumschiffs durch die Gravitation der Erde) und erreicht in einiger Entfernung ein massereiches Objekt, um den es im Flyby eine Kehrtwende um 180° macht, ohne an Geschwindigkeit einzubüßen (also ohne die gravitationsbedingte Beschleunigung bei Annäherung bzw. Abbremsung bei Entfernung, ganz wie beim Wegflug von und späteren Rendezvous mit der Erde). Am Ende berühren sich die Sensoren erneut und geben diesmal den Uhrenstand an den jeweils anderen weiter.
Während die Erduhr 2,2[Periode] Sekunden zählte und 23 Signale absandte, zählte die Raumfahreruhr 0,872 Sekunden und entsandte 9 Signale.
Der Knackpunkt ist der, daß es am Anfang wie am Ende dieses Szenarios einen Uhrenabgleich gab. Wenn zwei Beobachter sich zueinander in Bewegung befinden, sich aber nur aus der Entfernung beobachten,
ohne zuvor und später Kontakt zu haben, ist ihre "Beobachtung" (also die Ermittlung des Vorganges nach Herausrechnen des Dopplereffektes) durchaus symmetrisch. Jedenfalls so symmetrisch, wie es beim Ermitteln deutlich abweichender Distanzen und (gezählter) Signalmengen sein kann (symmetrisch ist die Menge der empfangenen Signale pro Sekunde im ruhenden System).
Doch in meinem Beispiel mit den beiden Kontakten wird der Raumfahrer, der für die sich ihm annähernde Erde eine Entfernung von 3,924 Lichtsekunden ermittelt hat, am Ende feststellen, daß sie
nicht wie aus dem Dopplereffekt ermittelt 3,924 Lichtsekunden entfernt gewesen sein und
nicht für die Annäherung 4,36 Sekunden (Raumfahrerzeit) gebraucht haben kann. Der Erdbeobachter hingegen wird seine ermittelten Zeiten und Entfernungen hingegen bestätigt finden.
Wenn Du willst, dann rechne das ganze doch mal für folgende Situation aus. Zwei Raumschiffe fliegen aneinander vorbei und starten ihre Uhren durch Kontakt zweier Sensoren. Das eine fliegt mit 0,9c, das andere mit 0,95c. Nach einer Lichtsekunde Fluges macht das letztere Schiff einen Flyby und fliegt dem langsameren Raumschiff nach. Beim Rendezvous berühren sich die Kontakte wieder und übermitteln die Uhrenstände. Auch in diesem Beispiel wird der Raumfahrer des schnelleren Schiffes feststellen, daß seine ermittelten Daten falsch sein müssen, er also einer Dilatation ausgesetzt sein muß. Aber der andere wird zumindest keine eindeutigen Ergebnisse pro Dilatationsfreiheit erhalten, sondern einen Spielraum, sodaß er annehmen darf (nicht muß), ebenfalls einer Dilatation zu unterliegen. Vermute ich mal.
Original anzeigen (5,3 MB)perttivalkonen schrieb am 07.09.2017:Darüber, wie viel jene gesehene bewegte Uhr beim nächsten Uhrenvergleich von der eigenen Uhr abweicht, darüber verrät dieser Dopplereffekt schnellerer oder langsamerer Uhren gar nichts. Erst wenn man diesen Dopplereffekt herausrechnet und sich auf die übrigbleibende Zeitdilatation bezieht, erst dann kann man den künftigen Uhrenvergleich prognostizieren.
Original anzeigen (5,3 MB)
