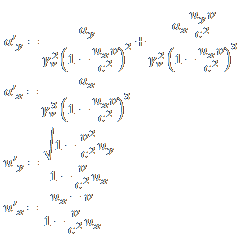Schwierigkeit der Längenkontraktion

mojorisin schrieb:DAs ist eigentlich völliger Kokolores

Schon frech Formeln aus dem Zusammenhang zu reißen.
Der Kontext war folgender: Beitrag von pluss (Seite 69)

mojorisin schrieb:WIr waren uns einig das die GEschwindigkeit mit der Bob die Kugel misst als u'y bezeichnet wird.

Nein, vielleicht bist du dir da mit @Zotteltier drüber einig. Ich streite strickt ab das es sich bei den gestrichenen Werten um Messergebnisse von Bob aus seinem System handelt.

Wenn ihr glaubt das es sich bei den gestrichenen Werten um Bobs Messergebnisse handelt, erklärt mir mal womit er t' gemessen hat.

@mojorisin | @Zotteltier

Also @pluss ist doch ohne Frage hier völlig überfordert, er versteht doch schon die Grundlagen nicht mal im Ansatz, zeigt auch wieder diese Aussage Hier:

pluss schrieb:Das du die gestrichenen Werte für Messeresultate von Bob in seinem System hältst, ist dein Problem und zeigt nur dein Unverständnis der Lorentztransformation.

Den Schwachsinn hat er ja schon mehrfach geschrieben, er begreift die elementarsten Grundlagen kein Stück nicht.

Natürlich sind gestrichene Werte eben die Werte, welche Bob in seinem System messen wird, ungestrichen sind die Werte, welche Alice misst. @pluss schnallt einfach gar nichts und dazu kommt dann noch seine Arroganz.

Er erklärt auch nicht, was denn gestrichene Werte nach seinem Glauben sein sollen. Konkret nannte er diese mal "nur errechnete Werte", ...

---

Und auch das hier:

pluss schrieb:... und die hinten ihm liegende Strecke wird für ihn Länger.

zeigt, von der SRT versteht er nicht ein Wort wirklich. Ein Myon fliegt durch die Atmosphäre, nach der SRT ist die Strecke der ganzen Atmosphäre lorentzkontrahiert, ganz sicher ist nicht nur die Strecke vor dem Myon kontrahiert, sondern die ganze Strecke, also auch die hinter dem Myon. Und ebenso ganz sicher wird die Strecke hinter dem Myon nicht länger.

Dazu wird der @pluss aber uns hier auch nie eine Rechnung zeigen, wenn er sich nur mal ein wenig an das halten würde, was er von anderen fordert ...

@pluss

pluss schrieb:Nein, vielleicht bist du dir da mit @Zotteltier drüber einig. Ich streite strickt ab das es sich bei den gestrichenen Werten um Messergebnisse von Bob aus seinem System handelt.

Frage 1: Für welches Inertialsystem steht denn dann deiner Meinung nach das gestrichene System, also z.B. u'_y?
Frage 2: Wie bezeichnest du dann Werte wie sie Bob messen würde?

@mojorisin

Weißt Du, die Härte ist doch eigentlich, dass nun nach der ganzen Zeit solche falschen Aussagen von @pluss kommen. Nach dem man ihm nun lange erklärt hat, wie das mit den Systemen ist, wie da die Werte bezeichnet werden, kommt er mit so einem Mumpitz daher.

Und diese Dinge sind ja nun auch bei Newton schon genau so, auch da gibt es diese Notation, auch da wird zwischen zwei Systemen, also zwischen S und S' mit einer Transformationsgleichung transformiert. Nur wird da die Galilei-Transformation (GT) genommen und nicht die Lorentz-Transformation (LT).

Da @pluss hier immer wieder deutlichst zeigt, er scheitert schon an Newton, beherrscht nicht mal eine normal Koordinatentransformation zwischen S und S' mit der GT, er versteht gar nicht, was die transformierten Werte bedeuteten, kann er natürlich an der SRT nur ebenso scheitern.

pluss schrieb:Schon frech Formeln aus dem Zusammenhang zu reißen.

Aha, ich erinnere dich nochmal an deine Diagramme:

pluss schrieb am 25.11.2017:Vielleicht wäre Dir aufgefallen das deine Diagramme nicht korrekt sein können, wenn du auch die Transformierten Werte in Diagrammen dargestellt hättest.
Ich kann meine Diagramme für die Transformierten Werte ruhigen gewissen hier einstellen:

Da ist eindeutig a'_y = 0 aber u'_y ändert sich. Oder willst du gar diese Tatsache hier auch noch abstreiten.


Also, daher nochmal de Frage: Wofür steht das gestrichene System? Ungestrichen steht für Alice und gestrichen?

Aber halt warte da kommt noch was, du hattest ja mal so schöne Exceltabellen gemacht, hier:
Beitrag von pluss (Seite 34)

Kleines Bild gefälligst:


Und wie nanntest du dort das IS von Bob? Natürlich S'

Zitat @pluss:

pluss schrieb: Ich streite strickt ab das es sich bei den gestrichenen Werten um Messergebnisse von Bob aus seinem System handelt.

mojorisin schrieb:Wieso bist du dir sicher? Hast du es simuliert?

...simuliert nicht, - aber ich habe Vorstellungsvermögen.

Du übersieht da ein Problem:

Egal wie das Zahnrad sich verformt - entspricht eine Umdrehung der Achse in dem Beispiel 3m.

mojorisin schrieb:So könnte man z.B. folgenden Sachverhalt untersuchen.Ereignis A: Punkt 1 des Rades trifft auf Punkt 1 der StraßeEreignis B: Punkt 2 des Rades trifft auf Punkt 2 der Straße. Das Ereignis A und B stattgefunden haben, darüber sind sich alle einig. Wie weit allein der räumliche Abstand oder allein der zeitliche Abstand zwischen den Eregnissen ist, darüber sind sich die Beobachter jedoch uneinig. Nur der raumzeitliche Abstand, also der Pythagoras von räumlichen und zeitlichem Abstand wird von allen gleich wahrgenommen.

...mach es doch einfacher (wir gehen dazu davon aus, dass das Rad abrollt, bzw. nicht schleift):

Auf dem Rad - ist am äußersten Umkreis eine Lampe - die Alice beobachtet. Dazu hat das Rad an der gleichen Stelle einen Signalpunkt, der wenn er auf der Schiene ist, jeweils 1x pro Runde an der Schiene - welche über ein Wegemesssystem verfügt - eine Streckenzählung auslöst.

Alice beobachtet nun die Lampe sowie den Signalpunktzähler - und sieht die Anzahl der Umdrehungen (wenn Du Probleme hast bei vielen Umdrehungen, stell Dir halt ein großes Rad vor, z.B. statt 3m Umfang eins mit 300000000m Umfang).

Alice wird nun die Anzah der Umdrehungen sehen, sowie das jedesmal wenn das Licht unten ist, sich die Streckenzählung um "X" Meter erhöht.

Was meinst Du wieviel "X" Meter jedesmal ist?

-------------------------------------------------------------------------

...falls Du jetzt denkst das wir das alles schon durchgekaut haben...rechne Dir mal aus wieviel UMFANG pro Umdrehung - in jeweils Bob's und Alice System - pro Raddrehung abgerollt werden muss - denn dann wirst Du ggf. erkennen, das umso höher die Geschwindigkeit wird....es ggf unmöglich wird, was Du mit Deinen Bildern bezüglich verformter Zahnräder ausdrücken wolltest.

@GuggstDu

GuggstDu schrieb:...simuliert nicht, - aber ich habe Vorstellungsvermögen.

Das ist ja schön und gut, aber hast du auch Erfahrungen mit der 4D Minkowski-Welt, oder basiert dein Vorstellungsvermögen doch auf der herkömmlichen 3D Newton Welt. Ich tippe auf letzteres ich habe noch von keinem Menschen gehört der wirklich 4D Vorstellungsvermögen hat.
Fundierte, physikalisch richtige Vorhersagen basieren dann auf angewander Mathematik, die uns hilft einige Streiche die uns unser Gehirn vorgaukelt aus dem Weg zu gehen.

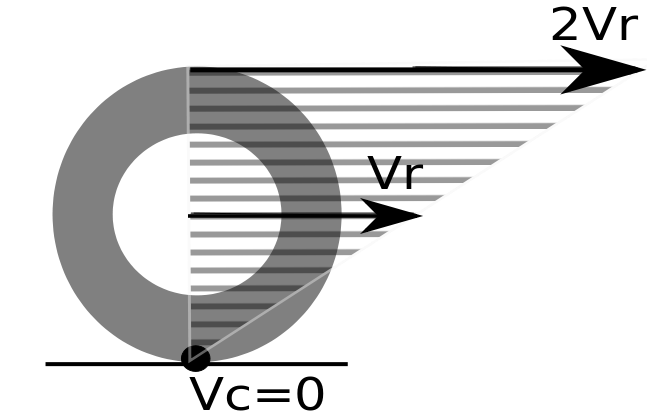
Ein Problem ist z.B. das du davon ausgehst das sich das Rad homogen dreht so wie wir es von jedem herkömmlichen Auto kennen. Da ist dann die Winkelgeschwindigkeit des Rades unabhängig vom Radius und der Höhe, und Die Geschwindigkeit eines Punktes des Rades berechnet sich einfach zu:



WEnn wir wissen wollen wieviel Strecke s ein Punkt zurückgelegt hat, multiplizieren wir einfach Die GEschwindigkeit eines Punktes mit der Zeit:


Man könnte obige Gleichung auch als Integral über v schreiben, so wie man das normalerweise macht, da aber v eine Konstante ist, reicht es aus v einfach mit der Zeit zu multiplizieren.

Im relativistischen Fall, und das habe ich im vorigen Post schon erwähnt und wurde von dir einfach ignoriert, hängt \omega selbst und damit auch v je nach Beobachter vom Radius, der Zeit und der Höhe ab. Die abgerollte Strecke ist dann ein kompliziertere Funktion, die nur über ein Intergral erhalten werden kann.

GuggstDu schrieb:Was meinst Du wieviel "X" Meter jedesmal ist?

Ich kann es dir so nicht sagen, denn wie gesagt das, benötigt etwas Rechenaufwand.

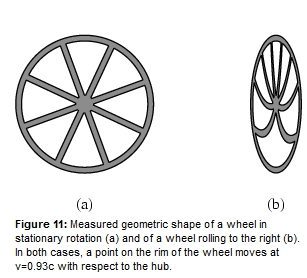
GuggstDu schrieb:denn dann wirst Du ggf. erkennen, das umso höher die Geschwindigkeit wird....es ggf unmöglich wird, was Du mit Deinen Bildern bezüglich verformter Zahnräder ausdrücken wolltest.

Die Zahnräder sollen ja auch nur eine Veranschaulichung sein, und kein Beweis für die Existenz solch schnell rotierender Räder.
Generell sehe ich aber momentan immer noch keinen Grund das ein Rad aus Sicht unterschiedlicher Inertialsysteme unterschiedliche Strecken abrollen kann. Des WEiteren gilt, das wenn ein Rad rutscht, dann muss das auch von allen Beobachtern so gesehen werden denn es gilt: Berührt ein bestimmter Punkt des Rades mehrere Punkt der Straße muss es das für alle Beobachtger tun. Den nwenn ein Punkt des Rades einen Punkt der Straße berührt ist das ein bestimmtes Ereignis das in der Raumzeit stattgefunden hat, und wenn ein Eregniss stattfindet, dann muss es das auch für alle Beobachter tun. --> Ob ein Rad also rutscht oder rollt, darüber müssen sich unterschiedliche Beobachgter einig sein.

Das das ganze aber nicht mehr nur so einfach anhand des VOrstellungsvermögens abgehandelt werden kann, sieht man z.B im BUch von G. Rizzi: "Relativity in Rotating Frames: Relativistic Physics in Rotating Reference Frames"

Hier ein Link zu Google Books, bei dem z.B. die verdrehten Speichen saimuliert sind:
Spoilerhttps://books.google.de/books?id=RW4PCQAAQBAJ&pg=PA321&lpg=PA321&dq=The+positions+of+points+on+a+rolling+ring+at+retarded+points+of+time+were+calculated&source=bl&ots=T66lT6T2o1&sig=c9RTfB1Sop6oqJQHm5CoizL2YAI&hl=de&sa=X&ved=0ahUKEwj30eGYmoLYAhWDCewKHS6TDPAQ6AEILzAB#v=onepage&q=The%20positions%20of%20points%20on%20a%20rolling%20ring%20at%20retarded%20points%20of%20time%20were%20calculated&f=false

Des WEiteren gibt es auch einen Simulator der ein ähnlices GE veranschaulicht:

http://www.relativitysimulation.com/MainWebPageAlpha.html

Hier ist das Auto aus SIcht der Straße:
http://www.relativitysimulation.com/Documents/Car_from_Road.webm

Hier ist das Auto aus Sicht des Fahrers
http://www.relativitysimulation.com/Documents/Car_from_Driver.webm

DAs müssen jetzt aber nicht unbedingt die besten SImulatoren sein. Generell gilt aber, das das Thema "relativistische Winkelgeschwindigkeiten" doch schon eher anpruchsvoller Stoff der Physik ist, und Schlussfolgerungen fundiert sein sollten.

mojorisin schrieb:Ich kann es dir so nicht sagen, denn wie gesagt das, benötigt etwas Rechenaufwand.

Nein, es benötigt keinen Rechenaufwand, denn wir hatten ja darüber gesprochen das abgerollt wird. Und dann muss bei konstanter Geschwindigkeit halt die abgerollte Länge dem Umfang des Rades entsprechen - was allerdings aus Deiner Sicht problematisch werden wird.

X= Umfang des Rades (Immer)

@GuggstDu

GuggstDu schrieb:Nein, es benötigt keinen Rechenaufwand, denn wir hatten ja darüber gesprochen das abgerollt wird.

Schau hier

Titel: Relativistic description of a rotating disk

A consistent relativistic kinematic description of a rotating disk is given. The disk is described from the point of view of an inertial observer momentarily at rest relative to a point on the periphery of the disk, and as observed in a coordinate system SS′ rotating with the disk. The kinematic resolution of Ehrenfest’s paradox is stated. Also the following elements of the description are analyzed: (a) the transformation of time from an inertial system, where the axis of the disk is at rest, to SS′; (b) the spatial geometry in SS′; and (c) the velocity of light in SS′. The procedure for synchronization of the coordinate clocks on the disk is stated explicitly.

http://aapt.scitation.org/doi/abs/10.1119/1.9969

In dieser Veröffentlichung wird genau das berchnet was wir hier diskutieren, und dort sind Herleitungen über mehrer Seiten drinne. Formel (21) auf Seite 872 beschreibt dann auch die WInkelabhängigkeit der Winkelgeschwindigkeit ω aus Sicht des ruhenden Beobachters mit einer maximalne Winkelgeschwindigkeit bei 180° und einer minimalen WInkelgeschwindigkeit bei 0°.

Eine weitere Veröffentlichugnn zum Thema gabs dann später unter dem Titel:

"Relativistic description of a rotating disk with angular acceleration"
https://link.springer.com/article/10.1007/BF00708527

Leider sind die Arbeiten nicht öffentlich zugänglich:

Und hier noch sehr aktuell:

A relativistic trolley paradox

http://aapt.scitation.org/doi/pdf/10.1119/1.4942168

Schlusswort vom letzgenannten: " ...that the wheels move without slipping in the rail system in spite of the Lorentz contraction of the wheels and the time dilation.."

@mojorisin

...danke für die Links.

"We also explain two surprising facts. First that the shape of a rolling wheel is elliptical in spite of the fact that the upper part of the wheel moves faster than the lower part, and thus is more Lorentz contracted, and second that a Lorentz contracted wheel with relativistic velocity rolls out a larger distance between two successive touches of a point of the wheel on the rails than the length of a circle with the same radius as the wheels."

http://aapt.scitation.org/doi/pdf/10.1119/1.4942168

Stell Dir zu der Aussage oberhalb vor, das Alice das Licht auf dem oberen Teil des Rades schneller laufen sieht, als wenn es unten herum läuft.
Diese Aussage besagt, dass das Licht im oberen Teil des Rades schneller läuft - und zwar auf Grund der Längenkontraktion. Dieser Satz stimmt aber nur aus Bob's Sicht! (das hätte dort vermerkt werden müssen, bzw. das es die Sicht des Fahrers ist). Der 2te Teil den ich Fett gekennzeichnet habe, besagt genau das was ich sage: Der Umfang wird größer.

Für mich ist halt klar das Alice messen kann, welche Strecke das Licht am Rad zurück legt - und die Bestätigung dafür noch vom Signalpunktzähler erhält. Dazu kennt sie die Länge der Ruhestrecke und die Anzahl der Umdrehungen - bzw. wird für sie die Länge der Ruhestrecke nach "X" Umdrehungen erreicht (ihr ist ja "X" bekannt, denn sie hat ja mitgezählt), der Signalpunktzähler hat auch die Anzahl der Umdrehungen inklusive deren Länge ermittelt - was will sie mehr - hat sie von den langsamen Zügen doch gelernt, das die Strecke geteilt durch die abgerollte Länge der Räder die Anzahl der Umdrehungen ergibt. Es passt für sie also wie immer alles zusammen.

Dennoch muss sie Deiner Meinung nach einer fulminanten Täuschung unterliegen.

Ich hoffe das Du verstehen wirst, das ich da meine Probleme mit habe. Es wird ggf. auch nichts weiter bringen wenn wir uns darüber streiten wer Recht hat. Wir müssten es halt ausprobieren..

@GuggstDu

GuggstDu schrieb:Stell Dir zu der Aussage oberhalb vor, das Alice das Licht auf dem oberen Teil des Rades schneller laufen sieht, als wenn es unten herum läuft.
Diese Aussage besagt, dass das Licht im oberen Teil des Rades schneller läuft - und zwar auf Grund der Längenkontraktion. Dieser Satz stimmt aber nur aus Bob's Sicht! (das hätte dort vermerkt werden müssen, bzw. das es die Sicht des Fahrers ist).

Ich weiß im Prinzip was du meinst sehe deinen Satz aber sehr kritisch, da er implizieren könnte Licht ist nicht gleich schnell (entgegen dem ersten Postulat der SRT) und weil er Inertialsysteme durcheinanderwürfelt: ALice sieht Licht schneller aufgrund der Längenkontraktion aber nur aus Bobs Sicht.

GuggstDu schrieb:Für mich ist halt klar das Alice messen kann, welche Strecke das Licht am Rad zurück legt

Ich bin im Prinzip bei dir bei einer ganz einfachen Sache: Alice misst nach dem Abrollen eine bestimmte Strecke s die das Rad abgerollt hat. WO ich nicht bei dir bin, ist das das eine einfacher linearer Zusammenhang ist zur Drehgeschwindigkeit des Rades. Diesen gibt es nämlich aus Sicht von Alice gar nicht.

ALso was du hier geschrieben hast:

GuggstDu schrieb:X= Umfang des Rades (Immer)

DAs kann ja aus Alice SIcht gar nicht stimmen. Der einfache Umfange des Rades aus Sicht von ALice entspricht einer Ellipse, und ist somit verkleinert. Trotzdem wird eine größere Strecke abgerollt. Dieser Widerspruch wird im Link aufgearbeitet und eine Lösung präsentiert.

Ich kann nur nicht die interessanten Teile hier reinstellen, da es sonst Copyright Probleme gibt.

@GuggstDu

mojorisin schrieb:Ich kann nur nicht die interessanten Teile hier reinstellen, da es sonst Copyright Probleme gibt.

Ich habe einen Link gefunden der Open Access sein müsste:

https://oda.hioa.no/nb/a-relativistic-trolley-paradox (Archiv-Version vom 26.08.2017)

Von dort kann man direkt das PDF runterladen.

mojorisin schrieb am 10.12.2017:Frage 1: Für welches Inertialsystem steht denn dann deiner Meinung nach das gestrichene System, also z.B. u'y?

Beantworte du doch erst mal die noch offenen Fragen:

pluss schrieb am 10.12.2017:Wenn ihr glaubt das es sich bei den gestrichenen Werten um Bobs Messergebnisse handelt, erklärt mir mal womit er t' gemessen hat.

pluss schrieb am 10.12.2017:Wo kommt deiner Ansicht nach jetzt eine zusätzlich wirkende beschleunigende Kraft auf der y-Achse her?

pluss schrieb am 10.12.2017:Was wäre wenn zusätzlich eine Kugel auf der z-Achse hin und her pendelt. Würde die Kugel dann eine gleich große wirkende beschleunigende Kraft erfahren wie die Kugel auf der y-Achse?

Du solltest dich besser nicht so an deine Diagramme der Excel-Tabelle klammern. Ich hatte dich doch schon mal auf diverse Berechnungsfehler deiner Tabelle hingewiesen. Offensichtlich scheinst du es aber für unnötig zu halten sie zu korrigieren. Auch den Hinweis deine Tabelle doch mal mit Diagrammen der gestrichenen Werte zu ergänzen, nicht um mir eine Freude zu bereiten, sondern damit dir deine Fehler auffallen, scheinst du nicht für nötig zu erachten.
Nun habe ich deine Tabelle mal mit Diagrammen der Transformierten Werte vervollständigt:



Oh, schau an, bei dir gibt es sogar Überlichtgeschwindigkeit.
Sowas passiert wenn man relativistische Geschwindigkeiten nach Newton addiert. Obwohl ich dich auch darauf hingewiesen habe, argumentierst du hier immer noch mit den Werten deiner Tabelle.
Auch musst du erklären warum auf a_y und a'_y eine Beschleunigung vorliegt.
Auch musst du erklären warum u'_y nicht unverändert bei 0,5c bleibt, wenn es sich bei gestrichenen Werten doch um Beträge handeln soll, die Bob in seinem System messen würde.

mojorisin schrieb:Da ist eindeutig a'y = 0 aber u'y ändert sich. Oder willst du gar diese Tatsache hier auch noch abstreiten.

Warum sollte ich das abstreiten, käme ja der Behauptung "die Formeln der Lorentztransformation sind falsch" gleich.
Oder möchtest du behaupten sie sind Falsch?
Ich hoffe doch nicht, denn mit den Formeln habe ich deine Tabelle ergänzt:



P.S.: Bevor es in Vergessenheit gerät, möchtest du dich hierzu bitte auch noch äußern:

pluss schrieb am 09.12.2017: mojorisin schrieb:
Die Länge einer Strecke wird ja von dem ABstand zweier (oder mehrerer)Punkte definert.

Ja. Wo siehst du da Probleme?
Bob hat den Abstand (Bogenmaß) an den Berührungspunkten der Zähne im Ruhezustand gemessen und 1m erhalten.
Wenn das Zahnrad eine Umdrehung ausgeführt hat, muss die Zurückgelegte Strecke einer Länge von 12m entsprechen. Was der Länge im Ruhezustand entspricht.

pluss schrieb am 10.12.2017: mojorisin schrieb:
Was ist mit dem Impulserhaltungssatz?

Was soll damit sein, wo wird der bei mir verletzt?

P.P.S.: Downloadlink deiner von mir ergänzten Excel-Tabelle (xlsx):
https://mega.nz/#!jAsyAB6T!6OP-l8-27S-fDC0ZN25HgPwIrlOUPPgeSjQW1Jbp-vQ

@pluss

pluss schrieb:Beantworte du doch erst mal die noch offenen Fragen:

Und damit willst du dem aus dem Weg gehen?

mojorisin schrieb:Und wie nanntest du dort das IS von Bob? Natürlich S'

pluss schrieb: Auch den Hinweis deine Tabelle doch mal mit Diagrammen der gestrichenen Werte zu ergänzen, nicht um mir eine Freude zu bereiten, sondern damit dir deine Fehler auffallen, scheinst du nicht für nötig zu erachten.

Die WErte in den Tabellen sind die Ergebnisse der Transformation von Bobs System S' nach ALices System S du Knaller.

Ich hatte geschrieben:

mojorisin schrieb am 01.11.2017:Also zu den Berechnungnen anhand der Formel. Zuerst einmal definiere ich nochmal klar die Geschwindigkeiten und Beschleunigungen aus Sicht der unterschiedlichen Systemen zum Startzeitpunkt von Bob. Dabei ruht Bob relativ zu Alice und die Kugel bewegt sich für beide auf der y-Achse mit 0,5c.

______________________________
Bob:

für die Kugel:
u'y = 0,5c
u'x = 0c

Beschleunigung des Raumschiffs:

a'x = 10 m/s
a'y = 0 m/s

Das heißt Bob spürt eine Beschleunigung ziemlich genau gleich wie wenn er auf der Erdoberfläche stehen würde
_________________________________

Man kann die auch plotten, dann hat man gerade Linien, aber da die Werte ja konstant sind ist ein PLot für die Katz. Was du oben mit meiner Excel-Tabelle angestellt hast weiß ich nicht, wenn du aber die Rücktransformation von S nach S', die ja sinnlos ist, weil S hat man ja erst durch Transformation erhaltne, trotzdem machen willst, dann müssen oben genannte 4 Werte wieder raus kommen. Tuts das nicht hast du Murks gerechnet. Und nein das liegt nicht an meiner Excel tabelle sondern weil du die Rücktransformation falsch gemacht hast.

pluss schrieb:Oh, schau an, bei dir gibt es sogar Überlichtgeschwindigkeit.
Sowas passiert wenn man relativistische Geschwindigkeiten nach Newton addiert.

Nein sowas passiert wenn man von Tuten und Blasen keine Ahnung hat.

pluss schrieb:Warum sollte ich das abstreiten, käme ja der Behauptung "die Formeln der Lorentztransformation sind falsch" gleich

Beide Werte sind aus demselben INertialsystem da brauchst gar keine Lorentztransformation. Das zeigt nur das du null aber auch wirklich Null Ahnung von dem hast was du hier schreibst. Was du hier schreibst, und du merkst das nicht mal, ist äquivalent zur Aussage:
Das Auto bekommt immer höhrere Geschwindigkeit ohne das es beschleunigt. Das ist so trivial, ich kann nicht glauben das du das nicht checkst.

pluss schrieb am 10.12.2017:Wenn ihr glaubt das es sich bei den gestrichenen Werten um Bobs Messergebnisse handelt, erklärt mir mal womit er t′ gemessen hat.

Ja mit was hat Bob wohl seine Zeit gemessen? Sanduhr, Wanduhr, Armbanduhr, Wasseruhr ne Rolex wer weiß das schon? Vielleicht hat er auch den neuseten Strontium-Zeitmesser an Board:
https://www.welt.de/wissenschaft/article124108206/Forscher-praesentieren-die-praeziseste-Uhr-der-Welt.html

pluss schrieb:P.S.: Bevor es in Vergessenheit gerät, möchtest du dich hierzu bitte auch noch äußern:

Vergiss das Radproblem, ich hatte dazu folgende relative neue Veröffentlichung gepostet:

mojorisin schrieb:http://aapt.scitation.org/doi/pdf/10.1119/1.4942168

Schlusswort vom letzgenannten: " ...that the wheels move without slipping in the rail system in spite of the Lorentz contraction of the wheels and the time dilation.."

Kannst dir ja mal durchlesen und dann die, deiner Meinung nach, Fehler nennen.

pluss schrieb:Beantworte du doch erst mal die noch offenen Fragen:

Ne so wird das nix. Erstmal müssen wir klären was u' ist. Unsere Ansicht dazu kennst Du. Jetzt erläutere uns bitte Deine.

@mojorisin

mojorisin schrieb:Ich weiß im Prinzip was du meinst sehe deinen Satz aber sehr kritisch, da er implizieren könnte Licht ist nicht gleich schnell (entgegen dem ersten Postulat der SRT) und weil er Inertialsysteme durcheinanderwürfelt: ALice sieht Licht schneller aufgrund der Längenkontraktion aber nur aus Bobs Sicht.

Habe den Satz schnell "hingehunzt" - hier noch mal verständlicher:

"First that the shape of a rolling wheel is elliptical in spite of the fact that the upper part of the wheel moves faster than the lower part, and thus is more Lorentz contracted,"

Dieser Satz sagt aus, das der obere Teil des Rades sich schneller bewegt als der untere - und somit mehr Lorentz kontrahiert ist als der untere.

Denken wir nun an das mit umlaufende Signal-Licht auf dem Rad:

Aus der Sicht von Alice wird es im oberen Teil langsamer laufen - und schneller im unteren.
Aus der Sicht von Bob wird es im oberen Teil des Rades schneller laufen - und im unteren Teil langsamer.

Somit ist der Satz (s. Zitat weiter oben) aus meiner Sicht nicht richtig.

Oder meinst Du das Alice das Licht im kontrahierten Teil schneller laufen sieht als im nicht kontrahierten Teil?

mojorisin schrieb:Ich bin im Prinzip bei dir bei einer ganz einfachen Sache: Alice misst nach dem Abrollen eine bestimmte Strecke s die das Rad abgerollt hat. WO ich nicht bei dir bin, ist das das eine einfacher linearer Zusammenhang ist zur Drehgeschwindigkeit des Rades. Diesen gibt es nämlich aus Sicht von Alice gar nicht.

Alice verlässt sich da ganz auf den Streckenzähler und die Anzahl der Umdrehungen. Einen linearen Zusammenhang gibt es nicht.

mojorisin schrieb:DAs kann ja aus Alice SIcht gar nicht stimmen. Der einfache Umfange des Rades aus Sicht von ALice entspricht einer Ellipse, und ist somit verkleinert. Trotzdem wird eine größere Strecke abgerollt. Dieser Widerspruch wird im Link aufgearbeitet und eine Lösung präsentiert. Ich kann nur nicht die interessanten Teile hier reinstellen, da es sonst Copyright Probleme gibt.

Habe den Link und auch die vorherigen von Dir gut durchgelesen.

Klar, - das kann alles so sein - und es ist ein guter Erklärungsversuch. Doch sagt mir mein Bauchgefühl (weiß...ein dummes Wort) das da etwas nicht stimmt.

Deshalb möchte ich versuchen diese Erklärungen mit einem einfachen Beispiel zu widerlegen:

Nimm dazu an, das Rad hat 12 (eine a 30°) Lampen auf dem Umkreis angebracht. Aus der Sicht von Alice würden nun bei geringer Geschwindigkeit immer jeweils 6 Lampen im oberen Teil -gegen den Uhrzeigersinn- langsamer laufen - sowie jeweils 6 schneller im unteren Teil (oder denk es Dir andersherum, falls Du nicht meiner Meinung bist, das der langsamere Teil für Alice der obere Teil des Rades ist).

Sobald das Rad nun schneller läuft und auf Grund der Längenkontraktion zur Ellipse wird, entsteht dort, wo die jeweils in Laufrichtung vorne liegende schnellste Lampe "abbremst" (stellen wir uns das Rad als Uhr vor, dann wäre das bei 3:00Uhr) ein Problem - denn schieben wir nun im unteren Teil mit der gleichen Geschwindigkeit hinterher, dann würden immer mehr dieser Punkte für Alice im oberen Bereich des Rades laufen. Das wäre dann aber die kontrahierte Seite, - was sich aus meiner Sicht widerspricht. Und für Bob müssten dann ggf. mehr Lampen im unteren Teil laufen???

@Zotteltier

Zotteltier schrieb:Erstmal müssen wir klären was u' ist. Unsere Ansicht dazu kennst Du. Jetzt erläutere uns bitte Deine.

Nun ja, ein paar Aussagen dazu finden sich ja schon hier im Thread:

pluss schrieb am 07.11.2017:Was du offensichtlich nicht verstehen möchtest, bei a'_x handelt es sich weder um die von Alice in ihrem System beobachtete, noch um die von Bob in seinem System beobachtete Beschleunigung.

Da sagt er uns, was er glaubt, um was es sich bei a'_x nicht handelt.

Und hier:

pluss schrieb am 06.11.2017:Aus den eingesetzten Werten in deiner Gleichung geht dein Irrtum doch schon hervor, du hältst den Betrag von a'_x augenscheinlich für den Betrag, welchen Bob in seinen System messen würde. Das ist aber grundlegend falsch, bei a' handelt es sich um einen transformierten Wert von S nach S'.

erfahren wir dann, das er glaubt, es handelt sich bei a' nur um einen transformierten Wert von S nach S'.

Und ganz deutlich an @mojorisin gerichtet:

pluss schrieb am 06.11.2017:Was du und der Buntstifttäter nicht verstehst, bei u' und a' handelt es sich nicht um Beträge die Bob in seinem System beobachtet, sondern um Beträge die sich aus der Transformation von S nach S' ergeben.

Erklärt er dort nun, dass er glaubt auch bei u' handelt es sich nicht um einen Betrag, welchen Bob in seinem System "beobachtet", sondern "nur" um einen Betrag, der sich aus der Transformation von S nach S' ergibt.

Ich sage ja die ganze Zeit, da mangelt es ganz gewaltig am Grundlagenwissen, schon weit vor der SRT, schon mathematisch und nach Newton, da wird gar nicht verstanden, was eine Koordinatentransformation ist. Darum macht es kaum Sinn, sich über die SRT und solche Dinge zu "unterhalten".

@GuggstDu

GuggstDu schrieb:Doch sagt mir mein Bauchgefühl (weiß...ein dummes Wort) das da etwas nicht stimmt.

Das ist es wieder, Bauchgefühl wenn es um Betrachtungen im Minkowski-Raum geht. Es gibt nicht umsobnst gerade im Bereich Reltivitätstheorie soviel Paradoxa die letzendlich auf mathematischem Wege gelöst worden sind. Unser Bauchgefühl lebt ganz stark von unseren Erfahrungen und die sind mal nur vom alltäglichen Leben im Standard euklidischen Raum ohne Bewegungen im Grenzbereich der Lichtgeschwindigkeit. Keiner hat jemals nen Zug mit annährend c an sich vorbeirauschen gesehen. Und keiner hat jemals ein Rad sich zu ner Ellipse verformen gesehen.

Das die Lorentzkontraktion aber real stattfindet sieht man z.B. am sich ändernden Wirkungsquerschnitt bei Protonenkollisionen nachweisen.

GuggstDu schrieb:Klar, - das kann alles so sein - und es ist ein guter Erklärungsversuch.

Naja, es ist zumindest eine wissenschftliche Peer-Reviewed Veröffentlichung mit mathematisch fundierter Herleitung, ich würd sagen das is n bissl mehr als ein guter Erklärungsversuch.

GuggstDu schrieb: Aus der Sicht von Alice würden nun bei geringer Geschwindigkeit immer jeweils 6 Lampen im oberen Teil -gegen den Uhrzeigersinn

Ok, bevor wir aneinander vorbeireden: Ich stelle mir das so vor das Alice am Straßenrand sitzt und das Rad von links nach rechts vorbeirollt. Dabei hat der Mittelpunkt die Geschwindigkeit v. Dann muss sich
1. Das Rad rechts herum drehen
2. die Geschwindigkeit am obersten Punkt muss dann die höchste sein mit V_{Punkt} = v + \omega \cdot r während der untere Punkt der die Straße berührt gegenüber AQlice ruht.

Das ganze sieht dann so aus:

So zumindest die Ausgangsdefinition im Paper wobei dann diese Bild zustande kommt:


Quelle: http://www.spacetimetravel.org/tompkins/node7.html

GuggstDu schrieb:Und für Bob müssten dann ggf. mehr Lampen im unteren Teil laufen???

Wieso? Bob ruht ja relativc zum Rad. WEnn die Lampen alle im gleichen Abstand zur Mitte aufgebracht sind, warum sollten die sich dann unterschiedlich schnell drehen?

mojorisin schrieb:Ok, bevor wir aneinander vorbeireden: Ich stelle mir das so vor das Alice am Straßenrand sitzt und das Rad von links nach rechts vorbeirollt. Dabei hat der Mittelpunkt die Geschwindigkeit v. Dann muss sich 1. Das Rad rechts herum drehen 2. die Geschwindigkeit am obersten Punkt muss dann die höchste sein mit V_{Punkt} = v + \omega \cdot r während der untere Punkt der die Straße berührt gegenüber AQlice ruht.

Ok, - halten wir uns daran.

Wie kommst Du darauf das aus der Sicht von Alice die Lichtpunkte - an dem zur Ellipse gewordenen Rad- oben/im oberen Teil der Ellipse (kontrahierter Teil) schneller laufen, als unten?

@GuggstDu

GuggstDu schrieb:Wie kommst Du darauf das aus der Sicht von Alice die Lichtpunkte - an dem zur Ellipse gewordenen Rad- oben/im oberen Teil der Ellipse (kontrahierter Teil) schneller laufen, als unten?

DAs hat erstmal nicht mit SRT zu tun sondern generell. Hilft dir dieses Gif?


Wikipedia: Rollen

ansonsten hier:


Wikipedia: Rollen#Geschwindigkeit beliebiger Punkte

Der unterste Punkt des Rades, wo es die Straße berührt, hat eine Geschwindigkeit von null bezüglich der Straße, und der oberste Punkt bewegt sich nach vorne mit der doppelten Mittelpunktsgeschwindigkeit.

Achtung, der letzte Satz gilt natürlich nur unter nichtelativistischer Betrachtung.

Generell gilt: Da wo das Rad die Straße berührt, und das Rad nicht rutscht, das muss der UNterschied der Geschwindigkeit zwischen Straße und Reifen = 0 sein. Ist ja auch logisch rutscht das Rad, hat man eben eine GEschwindigkeit zwischen AUflagepunkt des Reifens und der Straße. Ob ein Rad rutscht oder nicht, ist lorentzinvariant, das heißt entweder alle sehen es rutschen oder keiner.