mojorisin schrieb am 16.12.2017:Da es sich um eine beschleunigte Bewegun handelt und man den Lorentzfaktor für jeden Schritt neu ausrechnen muss, man nennt das ein numerische Berchnung, ist die Schrittweite entscheidend. WIrd die zu groß ist die Annahme das man linear rechnet nicht mehr gegeben und die numerische Berechnung konvergiert nicht mehr.
Du hast vielleicht, ach was ziemlich sicher, keinen blassen SChimmer davon, aber du hast dann einfach mal verschiedene Sachen durchprobiert bis die Grafen nicht mehr gepasst haben und dachtest ich checks nicht.
Mit einem hast du recht, in deiner Tabelle darf weder die Schrittweite der Beschleunigung, noch die der Zeit vergrößert werden.
Umso erstaunlicher deine Schlussfolgerung aufgrund dieses Mangels:
mojorisin schrieb am 16.12.2017:Du hast vielleicht, ach was ziemlich sicher, keinen blassen SChimmer
Das Problem liegt nicht in der Wahl der Schrittweiten, sondern in deinen zum Teil selbstgebastelten nichtrelativistischen Formeln. Darauf hatte ich dich schon mehr als einmal hingewiesen. Keine Ahnung warum du diese Hinweise ignorierst. Fehlersuche ist gut und wichtig, allerdings sollte man diese auch, wenn nicht sogar insbesondere, auf die eigene Argumentation anwenden. Gut, wenn man sich selbst für unfehlbar und frei von jeglichen Irrtum halten sollte, ist die Fähigkeit der konstruktiven Selbstkritik meist weit entfernt, bei manchen hat sie vielleicht auch schon den Ereignishorizont von Sagittarius A* überquert.
Ich bin mir unsicher ob Sachargumente dich überhaupt noch erreichen, zum einen weil du auf solche nicht mehr eingehst, zum anderen weil du selbst keine mehr vorträgst. Ich versuche es trotzdem nochmal.
Zunächst einmal solltest du realisieren das die Werte des gestrichenen Systems gesucht werden. Diese Werte sind nur über eine Transformation der ungestrichenen Werte ermittelbar. Die Anfangsbedingungen des GE waren:
u_y=0{,}5c, u_x=0c, u_z=0c, v=0c.
Dann sollte auf der x-Achse eine Beschleunigung stattfinden, die endet wenn
u_x=0{,}7c beträgt.
Die Schrittweiten unabhängige Lösung lautet[1]:
u_x= \frac {dx} {dt}= \frac {a(t-t_0)} { \left [ 1+a^2 \left(t-t_0 \right)^2/c^2 \right ] ^{0,5}}
Was jetzt noch berücksichtigt werden muss sind die vor der Beschleunigung vorhandenen Geschwindigkeitskomponenten aller Achsen, also
x, y, z. Diese müssen ja noch dazu addiert werden. Es sollte klar sein, das hier nicht algebraisch addiert werden kann, sondern das Additionstheorem für relativistische Geschwindigkeiten angewendet werden muss. Wäre
u_x zu Beginn der Beschleunigung z.B. nicht
0c sondern
0{,}5c und
u_y=0c, müssten die Geschwindigkeiten wie folgt addiert werden[2]:
u=u_x=v \parallel u= \frac {v+ \frac {dx} {dt}} {1+v \frac {dx} {dt}}
Nun ist es aber so, das laut dem GE nicht auf der
x-Achse eine Geschwindigkeit vorliegt, sondern auf der
y-Achse. Hier müssen also nicht parallele Geschwindigkeiten, sondern eine senkrechte zur ebenen Geschwindigkeit addiert werden. Das geht wie folgt[3]:
u=v \perp u=\sqrt{u_y^2+ \left (\frac {dx} {dt} \right )^2 - \frac {u_y^2 \left ( \frac {dx} {dt} \right )^2} {c^2} }
u_x=v \perp u=\sqrt{ \left (\frac {dx} {dt} \right )^2 - \frac {u_y^2 \left ( \frac {dx} {dt} \right )^2} {c^2} }
Den Betrag für
u erhält man dann über die Vektoraddition
u= \sqrt {u_x^2+u_y^2}Mehr braucht es nicht um die Werte des ungestrichenen Systems für jeden beliebigen Zeitpunkt zu erhalten.
Die Werte für das gestrichene System, also die hier gesuchten Beträge, erhält man über die bekannte Lorentztransformation[4][5].
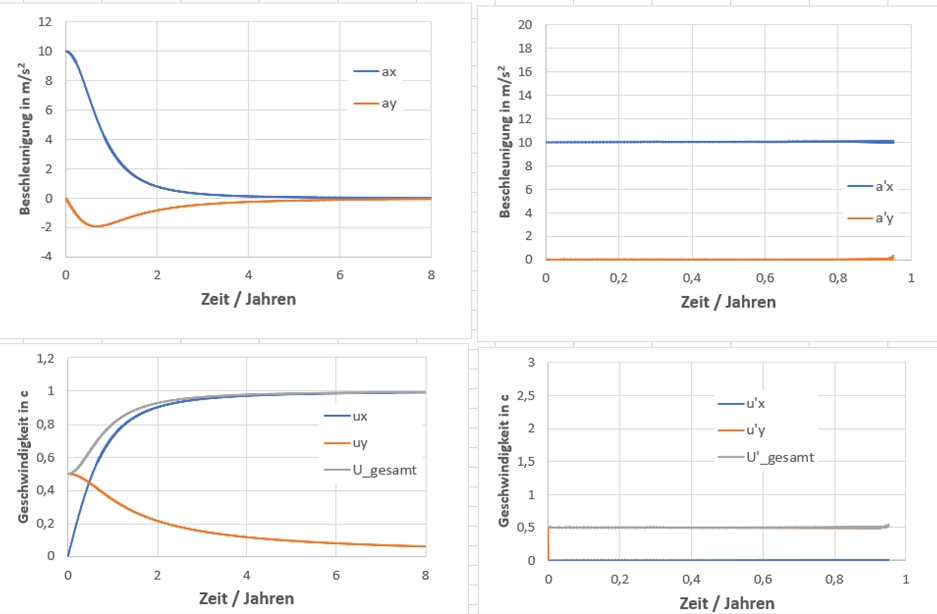
Das die Schrittweiten in Bezug auf die Beträge keine Rolle spielen, geht aus den folgenden Diagrammen hervor:
Schrittweiten:
a_x=210{.}000{.}000 \frac m {s^2}, t=0{,}05s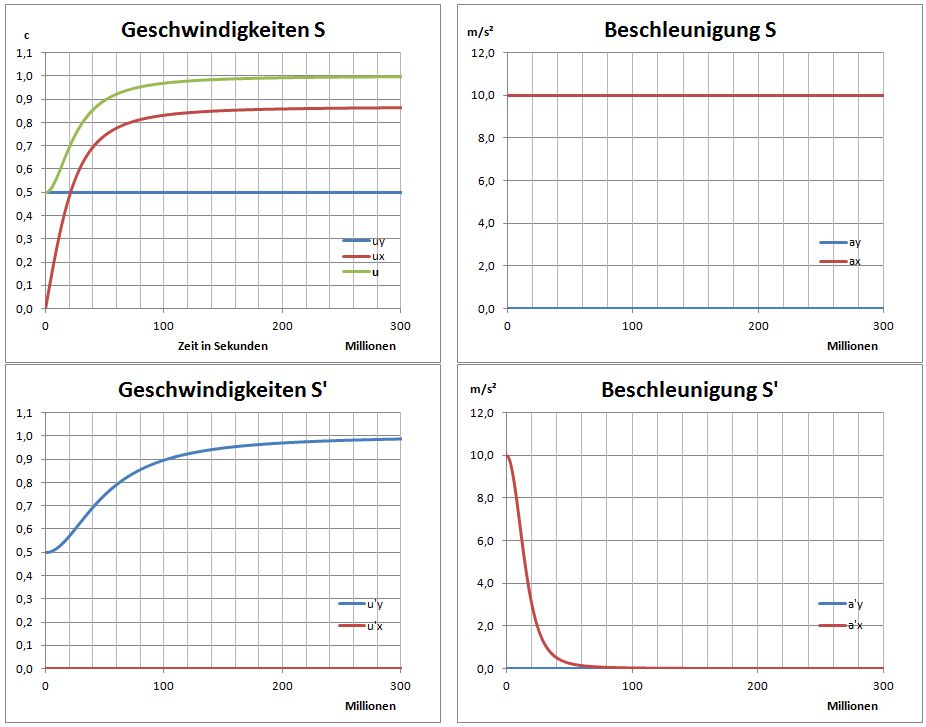
Schrittweiten:
a_x=10 \frac m {s^2}, t=10{.}000sNochmals kurz zu deiner behaupteten Beschleunigung auf der
y-Achse. Ich hatte in der Diskussion darüber
extra ein Zitat aus dem Lehrbuch[1] gewählt, um deinen Irrtum aufzuzeigen. Leider scheinst du auch diesen Hinweis zu ignorieren. Vielleicht lässt du dich mit Logik überzeugen; Die von dir angewendete Formel zur Berechnung von
a_y ist zwar korrekt, allerdings findet sie nur Anwendung, wenn eine Beschleunigung auf der
y'-Achse vorliegt. Eben diese liegt nicht vor, was auch aus deiner Tabelle hervorgeht. Die Tatsache das du die Formel trotzdem anwendest führt zu einem Zirkelschluss, der dir nur deshalb nicht auffällt, weil du keine Transformation
a_y \Longrightarrow a_y' respektive
a_y \Longleftarrow a_y' durchführst. Denn wenn
a_y' = 0 ist, muss auch
a_y = 0 betragen. Trotzdem setzt du den Betrag
0 für
a_y' in allen Berechnungschritten für
a_y ein. Der Zirkelschluss entsteht, weil
a_y' nur über eine Transformation von
a_y erhalten werden kann, die Formel für
a_y sich jedoch wiederum auf
a_y' bezieht. Das hätte dir im Grunde spätestens nach lesen meiner Frage, oder bei Darstellung der gestrichenen Werte auffallen müssen. Gut, vielleicht ist es dir aufgefallen, zumindest wäre es eine Erklärung dafür, das in deiner Excel-Tabelle das gestrichene System nicht dargestellt wird, und du dich um Beantwortung der Frage drückst:
pluss schrieb am 10.12.2017:Wo kommt deiner Ansicht nach jetzt eine zusätzlich wirkende beschleunigende Kraft auf der y-Achse her?
Was wäre wenn zusätzlich eine Kugel auf der z-Achse hin und her pendelt. Würde die Kugel dann eine gleich große wirkende beschleunigende Kraft erfahren wie die Kugel auf der y-Achse?
mojorisin schrieb am 16.12.2017:Hier hast du dasselbe in grün versucht. Keinen wintzigen blassen von der Materie aber hier einen auf Möchtegernwissenschaftler machen und versuchen meine Daten irgendiwe durch den Fleischwolf zu drehen. Meine Fresse ist das armselig.
Ich weise dich lediglich auf Fehler in deiner Excel-Tabelle hin, denen du sachlich offensichtlich nichts entgegenzusetzen hast. Auch dein Dysphemismus kann nicht über deine eigenen Fehler hinwegtäuschen.
mojorisin schrieb am 09.12.2017:Woher soll denn die Beschleunigung deiner Meinung nach auf der y-AChse herrühren?
Was ist mit dem Impulserhaltungssatz?
Warum stellst gerade du mir diese Frage?
Bei mir findet auf den
yy'-Achsen keine Beschleunigung statt. Du selbst bist es der behauptet eine Beschleunigung auf der
x-Achse führt zwangsweise auch zu einer Beschleunigung auf den
yy'-Achsen. Das behauptest du hier schon eine gefühlte Ewigkeit, belege hast du dafür trotz nachfrage bisher nicht geliefert.
Das deine Behauptung unzutreffend ist, lässt sich anhand meiner
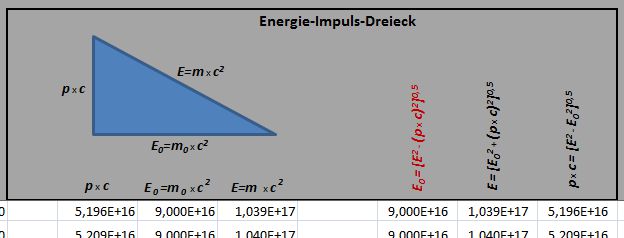
Excel-Tabelle belegen. Die habe ich nicht nur um Spalten für Impuls und Energie beider Systeme erweitert, sondern auch um ein "Energie-Impuls-Dreieck". Auf dieses kann der "Satz des Pythagoras" angewendet werden. So lässt sich schnell und einfach Belegen ob eine Verletzung der Energie- und/oder Impulserhaltung vorliegt, was bei mir, Belegt durch
E_0^2=E^2- \left (pc \right )^2=invariant, offenbar nicht der Fall ist.
In meiner Excel-Tabelle finden nur Formeln aus der Fachliteratur, auf die du dich zum größten Teil selbst berufst, Anwendung. Wenn du keinen Fehler in den Formeln oder deren Anwendung aufzeigen kannst, solltest du die Ergebnisse der Berechnungen als korrekt anerkennen.
P.S.: Noch eine Anmerkung zur Diskussionskultur. Das ich nicht die hellste Lampe unter all den Leuchten hier bin, weiß ich selber. Ich diskutiere hier, in der Hoffnung meiner Birne etwas mehr Lumen verleihen zu können. Das gelingt am besten über konstruktive sachliche Kritik. Für die bin ich nicht nur offen, sondern fordere sie geradezu. Wäre dem nicht so, würde ich meine kostbare Zeit eher im UH verbraten. Ich hoffe die Pause hat dazu beigetragen das die Gemüter wieder ein Level erreicht haben, die eine Sachdiskussion ermöglicht, um gemeinsam herauszufinden welche Argumente widerspruchsfrei zu sein scheinen und somit eine näherungsweise korrekte Vorhersage der Geschwindigkeitskomponenten erlaubt.
P.P.S.: Dir, und natürlich auch allen anderen hier, wünsche ich einen guten Rutsch ins neue Jahr
Download der Excel-TabelleFormat xlsx, Größe ≈24MB. Da die Tabelle keine Makros enthält, müssen die Diagramme manuell den Schrittweiten angepasst werden um eine sinnvolle Darstellung zu erzielen.
[1] "Einführung in die Relativitätstheorie", 2. Auflage, Ray d'Inverno, Kapitel 3.7, Seite 55, von Wiley-VCH. ISBN: 978-3-527-40912-9
[2]
Wikipedia: Relativistisches Additionstheorem für Geschwindigkeiten#1. Beispiel[3] "Spezielle Relativitätstheorie (SRT)", A. Weingärtner, Seite 144, von BoD-Norderstedt. ISBN 978-3-7392-1944-8
[4]
Wikipedia: Acceleration (special relativity)#Three-acceleration[5]
Wikipedia: Velocity-addition formula#Standard configuration
