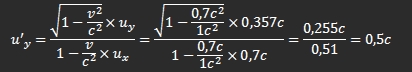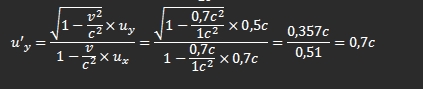Schwierigkeit der Längenkontraktion
07.12.2017 um 15:31@GuggstDu
Vor allem aus Sicht von Alice, und für diese Sicht gelten meine nachfolgenden Ausführungen, sind die Geschwindigkeiten der Punke and der Randfläche nicht mehr gleich.
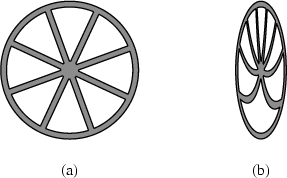
Man sieht das an diesem Bild, bei der die Speichen "verbogen erscheinen":
http://www.spacetimetravel.org/tompkins/node7.html
DAs liegt daran das zusätzlich zur Rotation noch die Translation kommt. Das heißt, aus Sicht von ALice ist der Punkt der zu einem Zeitpunkt t den Boden berührt in Ruhe und erfährt somit keine Zeitdilatation, hingegen bewegt sich der genau gegenüberliegende Punkt mit der Geschwindigkeit der Translation + Rotation, und Punkte die sich irgendow sonst befinden bewegen sich mit einer Geschwindigkeit in y-Richtung + Translation. Diese ganzen unterschiedlichen GEschwindigkeiten fürhren auch zu unterschiedlichen Zeitdilatation an den jeweiligen Punkten und müssen anhand der relativistischen GEschwindgkeitsaddition berechnet werden.
Sofort einsehbar ist allerdings, da für jeden Punkt eine unterschiedlicher GEschwindigkeitsbetrag exisitert, jeder Punkt einen anderen Lorenttfaktor besitzt.
Man kann sich leicht vorstellen das das ganze recht komplex wird und solch eine Bewegung nicht nur anhand des "menschlichen Verstandes" richtig erfasst werden kann, sprich man sollte Vorsicht walten lassen worauf man seine Schlussfolgerungen begründet.
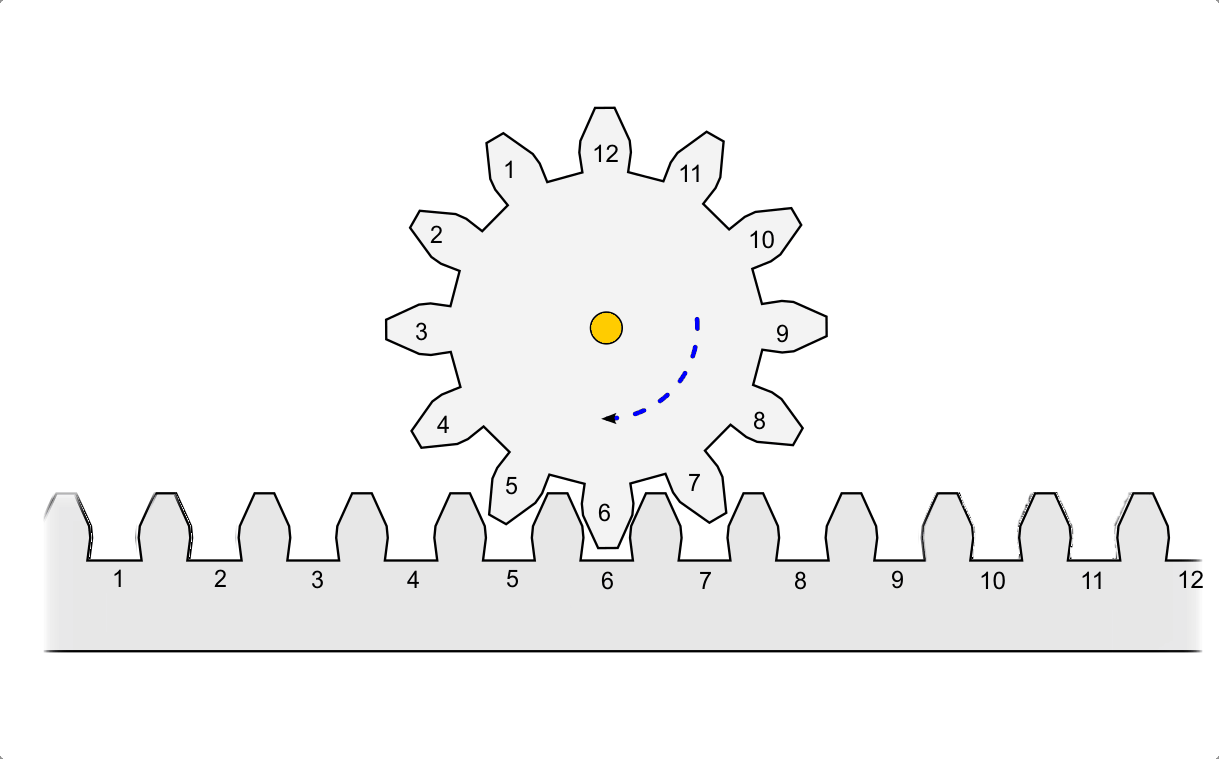
Die ganze Geschichte ist aus Sicht von unterschiedlichen Beobachter unterschiedlich komplex.GuggstDu schrieb:Alles prima. Nur ändert sich nichts daran, das bei einer Umdrehung der Achse des Zahn-, Mess-, oder Auto- Rades immer der gleiche Umfang abgerollt wird.
Vor allem aus Sicht von Alice, und für diese Sicht gelten meine nachfolgenden Ausführungen, sind die Geschwindigkeiten der Punke and der Randfläche nicht mehr gleich.
Man sieht das an diesem Bild, bei der die Speichen "verbogen erscheinen":

http://www.spacetimetravel.org/tompkins/node7.html
DAs liegt daran das zusätzlich zur Rotation noch die Translation kommt. Das heißt, aus Sicht von ALice ist der Punkt der zu einem Zeitpunkt t den Boden berührt in Ruhe und erfährt somit keine Zeitdilatation, hingegen bewegt sich der genau gegenüberliegende Punkt mit der Geschwindigkeit der Translation + Rotation, und Punkte die sich irgendow sonst befinden bewegen sich mit einer Geschwindigkeit in y-Richtung + Translation. Diese ganzen unterschiedlichen GEschwindigkeiten fürhren auch zu unterschiedlichen Zeitdilatation an den jeweiligen Punkten und müssen anhand der relativistischen GEschwindgkeitsaddition berechnet werden.
Sofort einsehbar ist allerdings, da für jeden Punkt eine unterschiedlicher GEschwindigkeitsbetrag exisitert, jeder Punkt einen anderen Lorenttfaktor besitzt.
Man kann sich leicht vorstellen das das ganze recht komplex wird und solch eine Bewegung nicht nur anhand des "menschlichen Verstandes" richtig erfasst werden kann, sprich man sollte Vorsicht walten lassen worauf man seine Schlussfolgerungen begründet.