mojorisin schrieb:Das weiter zu diskutieren erfordert nun aber das wir uns einig sind was du unter dem gestrichenen System verstehst und unter dem ungestrichenen.
mojorisin schrieb:Das weiter zu diskutieren erfordert nun aber das wir uns einig sind was du unter dem gestrichenen System verstehst und unter dem ungestrichenen.
Darüber sind wir uns doch einig, Alice ist das ungestrichene, Bob das gestrichene System.
Somit solltest du dich zu meiner Aussage auch äußern können, zustimmend oder eben auch nicht zustmmend:
 pluss schrieb:Die Ursache liegt in der Relativgeschwindigkeit.
pluss schrieb:Die Ursache liegt in der Relativgeschwindigkeit.
 mojorisin schrieb: pluss schrieb:
mojorisin schrieb: pluss schrieb:
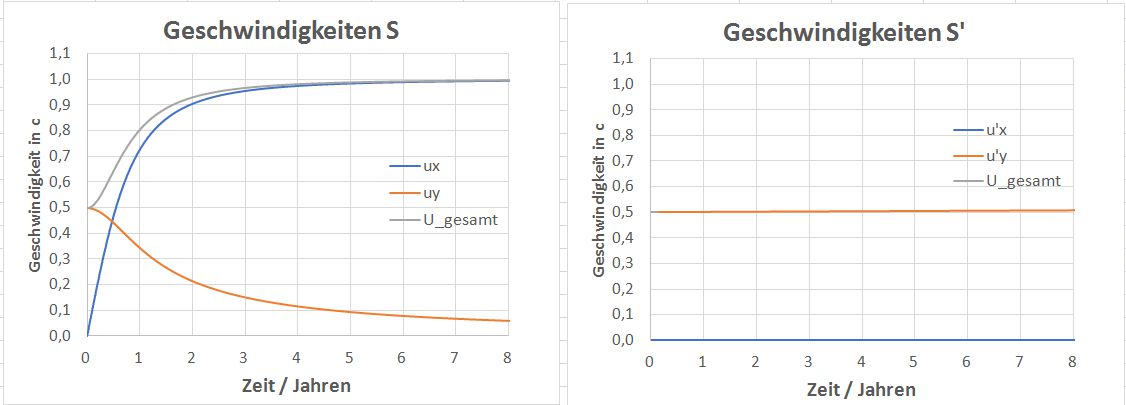
Dem stimme ich zu. Warum aber erwartest du das die Geschwindigkeitskomponente auf der y‘-Achse unverändert bleibt, es findet doch eine Beschleunigung statt, auf der x-Achse.
Basierend auf meiner Definition von oben. Für diese Antwort benötigen wir noch nicht mal Alice. Also u'y ist die Geschwindigkeit der Kugel wie sie Bob misst.
Woher willst du wissen was Bob misst?
Wieso sollte deine Vermutung hier zur Prämisse erhoben werden?
Halte dich bitte an das GE:
 pluss schrieb:Zunächst einmal solltest du realisieren das die Werte des gestrichenen Systems gesucht werden. Diese Werte sind nur über eine Transformation der ungestrichenen Werte ermittelbar. Die Anfangsbedingungen des GE waren: u_y=0{,}5c, u_x=0c, u_z=0c, v=0c.
pluss schrieb:Zunächst einmal solltest du realisieren das die Werte des gestrichenen Systems gesucht werden. Diese Werte sind nur über eine Transformation der ungestrichenen Werte ermittelbar. Die Anfangsbedingungen des GE waren: u_y=0{,}5c, u_x=0c, u_z=0c, v=0c.
Dann sollte auf der x-Achse eine Beschleunigung stattfinden, die endet wenn u_x=0{,}7c beträgt.
Hier muss zunächst einmal nachvollziehbar belegt werden welchen Betrag
u_y aufweist, wenn
u_x=0{,}7c beträgt. Welchen Betrag
u_y meiner Ansicht nach, nach der Beschleunigung auf der
x-Achse, aufweist, habe ich hier schon mehrfach nachvollziehbar belegt. Wiederhole es aber gerne nochmals:
Da es sich bei der Beschleunigung, wie auch der wirkenden Kraft, um Vektorielle Größen handelt, bleibt die Geschwindigkeitskomponente
u_y nach dem ersten und zweiten newtonschen Gesetzt unverändert. Das zweite newtonsche Gesetzt ist in der SRT zwar nur eingeschränkt Gültig, diese Einschränkung bezieht sich jedoch nur darauf, dass die Änderung der Bewegung nicht mehr proportional zur bewegenden Kraft verläuft. Es gilt folglich nicht mehr
\vec F=m \vec a, sondern
\vec F= \frac {m_0 \vec a} {\left (1- \frac {v^2}{c^2} \right )^{1{,}5}}. Da die wirkende Kraft in Richtung der
x-Achse zeigt, liegt auch keine wirkende Kraft auf der y-Achse vor, die eine Änderung der Bewegung auf der y-Achse hervorrufen bzw. erklären könnte.
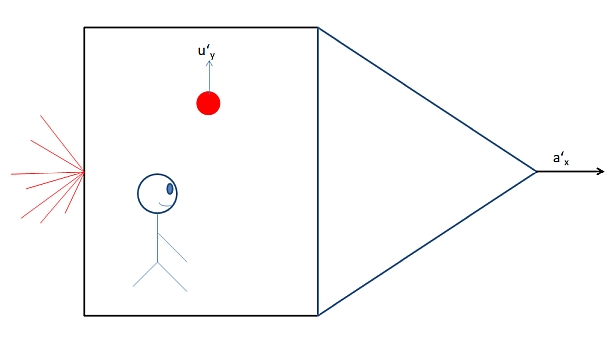
 mojorisin schrieb:Stellt die vor du bist Bob und sitzt im Raumschiff neben dir auf dem Schreibtisch die Kugel die mit 0,5c pendelt. Jetzt beschleunigst deine Rakete senkrecht zur Kugelbewegung. Würdest du jetzt erwarten das Bob plötzlich eine Änderung der Kugelgeschwindigkeit sieht.
mojorisin schrieb:Stellt die vor du bist Bob und sitzt im Raumschiff neben dir auf dem Schreibtisch die Kugel die mit 0,5c pendelt. Jetzt beschleunigst deine Rakete senkrecht zur Kugelbewegung. Würdest du jetzt erwarten das Bob plötzlich eine Änderung der Kugelgeschwindigkeit sieht.
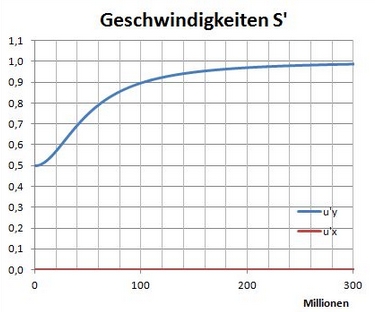
Was er sieht ist irrelevant, entscheidend ist was er messen würde. Da sich der Abstand der Wände (zwischen denen die Kugel pendelt) nicht verändert, womit gilt
L_y'=L_y, sich aber die Zeit mit der Relativgeschwindigkeit
t'<t verändert, würde ich erwarten das Bob eine höhere Geschwindigkeit der Kugel misst.
 mojorisin schrieb:Aber nur weil du davon noch nie gehört hast, ist das kein Argument das meine Berechnungsmethodik falsch ist.
mojorisin schrieb:Aber nur weil du davon noch nie gehört hast, ist das kein Argument das meine Berechnungsmethodik falsch ist.
Ich habe nie behauptet das eine numerische Berechnung falsch ist, sondern das deine Ergebnisse falsch sind und das mir eine numerische Berechnung hier ungeeignet erscheint:
 pluss schrieb:Oder könnten wir uns eventuell auf eine Schrittweiten unabhängige Berechnungsmetode einigen, die obendrein, statt ungefähre, zu jedem beliebigen Zeitpunkt exakte Werte liefert, weder Excel oder ähnliches voraussetzt, sondern nur einen Taschenrechner erfordert?
pluss schrieb:Oder könnten wir uns eventuell auf eine Schrittweiten unabhängige Berechnungsmetode einigen, die obendrein, statt ungefähre, zu jedem beliebigen Zeitpunkt exakte Werte liefert, weder Excel oder ähnliches voraussetzt, sondern nur einen Taschenrechner erfordert?
Denn nur so ist gewährleistet, das hier jeder unsere jeweiligen Ergebnisse schnell und problemlos nachvollziehen und überprüfen kann.
Welche Berechnungsmethode du letztendlich bevorzugst ist mir völlig egal, ich behalte meine aus oben genannten Gründen bei. Oder ist meine Berechnungsmethode Falsch?
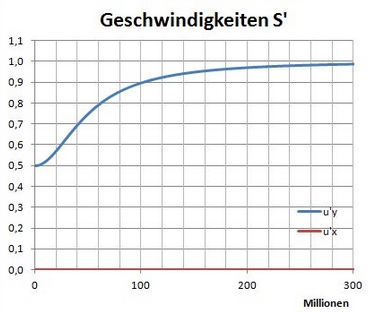
pluss schrieb:Warum stellst gerade du mir diese Frage?

pluss schrieb:Bei mir findet auf den yy′-Achsen keine Beschleunigung statt.