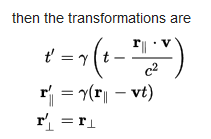Schwierigkeit der Längenkontraktion

nocheinPoet schrieb:u = (ux ; uy)
u = (ux ; u'yγ -1)
u = (ux ; 0,6 c ⋅ 1,667 -1)
u = (0,8 c ; 0,3599 c)

Und nun verstanden?

Ein Einfaches ja hätte es auch getan, wozu also wieder so eine Textwand.
Damit im Nebel nichts verschwindet:

Du behauptest also die Geschwindigkeit des Satelliten verringert sich auf der y-Achse für den Beobachter (S) allein dadurch, das der Satellit eine Beschleunigung auf der x-Achse erhält. Um beim obigen Beispiel zu bleiben: u_x=0,8c, u_y=0,36c.

Weiters:

nocheinPoet schrieb:aus dem Teilchen in der Uhr von Bob wird der Satellit, die Geschwindigkeiten bleiben aber wie gehabt

Folglich können wir den Begriff "Satellit" gegen "Kugel" (meiner Ur-Uhr) ersetzen.

Dass deine Aussage falsch sein muss, darauf hatte ich schon hingewiesen. Wie schon geschrieben, @mojorisin teilt (teilte) ja deine Ansicht, von dir aber augenscheinlich ignoriert:

mojorisin schrieb am 22.09.2017:Wenn du die x-Geschwindigkeit vorgibst dann wird automatisch die y-Geschwindigkeit kleiner. Wie Peter Lustig sagen würde: Klingt komisch ist aber so.

mojorisin schrieb am 22.09.2017:Richtig ist, während die Rakte kontinuierlich in x-Richtung beschleunigt, nicmmt für einen außenstehenden Beobachter die y-Geschwindigkeit kontinuierlich ab.

mojorisin schrieb am 22.09.2017:Deine y-Geschwindigkeit von 0,6c gilt nur solange die Rakte noch nicht in x-Richtung beschleunigt hat. Sobald sie anfängt in x-Richtung zu beschleunigen nimmt für den außenstehenden Beobachter die y-Geschwindigkeit sukzessive ab.

Darauf antwortete ich:

pluss schrieb:Aber eben nur bei Photonen, bzw. wenn ein Beobachter in seinem Inertialsystem etwas mit einer Geschwindigkeit von 1c beobachtet. Dein obiger Satz gilt gerade nicht für Objekte mit einer Ruhemasse >0. Abgesehen davon stünde das im Wiederspruch der Verschiebungsinvarianz: Wikipedia: Impulserhaltungssatz#Impulserhaltung_als_Folgerung_der_Homogenit.C3.A4t_und_Isotropie_des_Raumes

Also @mojorisins als auch deine "Überzeugung" verstoßen gegen die Impuls- und Energieerhaltung. Und komme mir nicht wieder mit Beweislastumkehr. Du musst die Widersprüche entkräften, denn bei mir entstehen sie ja nicht.

Wie der Impuls und die Energie eines Teilchens der Masse m in relativistischer Physik von der Geschwindigkeit v abhängen, folgt daraus, dass diese Größen für jeden Beobachter additive Erhaltungsgrößen sind.

Da die Lagrangefunktion nicht vom Ort x abhängt, (das heißt, die Komponenten xⁱ , i=1, 2, 3, sind zyklisch), ist die Wirkung invariant unter räumlichen Verschiebungen.

Hervorhebung (Unterstreichung) von mir.
Quelle: Wikipedia: Relativistischer Impuls

@pluss

pluss schrieb:Du behauptest also die Geschwindigkeit des Satelliten verringert sich auf der y-Achse für den Beobachter (S) allein dadurch, das der Satellit eine Beschleunigung auf der x-Achse erhält. Um beim obigen Beispiel zu bleiben: u_x = 0,8 c, u_y = 0,36 c.

Du und Deine "Interpretationen" ich behaupte nicht, physikalische Tatsache ist:

Wird die Geschwindigkeit des Satelliten im System S' mit u'_y =0,6 c gemessen, wird diese Geschwindigkeit im System S mit u_y = 0,36 c gemessen, wenn System S' sich mit u_x = 0,8 c gegenüber System S auf der x-Achse bewegt.

Sollte nun wirklich klar und verständlich sein, ohne dass Du da wieder eine neue "Interpretation" meiner Aussage kreieren musst. Im System S' gehen auch alle Uhren dilatiert, wenn diese im System S gemessen werden.

---

 

pluss schrieb:Dass deine Aussage falsch sein muss, darauf hatte ich schon hingewiesen.

Du behauptest nun viel, nur belegen kannst Du es nicht. Meine Aussage gibt genau das wieder, was man in der Fachliteratur zur SRT und der Zeitdilatation und der Addition und Transformation von Geschwindigkeiten lesen kann. Und, mal vorab, Impulse und Beschleunigung und was auch immer, spielt da keine Rolle. Es geht nur im die Geschwindigkeiten, welche in den jeweiligen Systemen gemessen werden.

pluss schrieb:Wie schon geschrieben, @mojorisin teilt (teilte) ja deine Ansicht, von dir aber augenscheinlich ignoriert:

mojorisin schrieb am 22.09.2017:Wenn du die x-Geschwindigkeit vorgibst dann wird automatisch die y-Geschwindigkeit kleiner. Wie Peter Lustig sagen würde: Klingt komisch ist aber so.

mojorisin schrieb am 22.09.2017:Richtig ist, während die Rakte kontinuierlich in x-Richtung beschleunigt, nicmmt für einen außenstehenden Beobachter die y-Geschwindigkeit kontinuierlich ab.

mojorisin schrieb am 22.09.2017:Deine y-Geschwindigkeit von 0,6c gilt nur solange die Rakte noch nicht in x-Richtung beschleunigt hat. Sobald sie anfängt in x-Richtung zu beschleunigen nimmt für den außenstehenden Beobachter die y-Geschwindigkeit sukzessive ab.

Er teilt meine Ansicht, noch immer, und er gibt eben die Aussagen der SRT richtig wieder, darum sind wir ja eben auch einig. Und ich ignoriere seine Aussagen nicht. Keine Ahnung wie Du darauf kommst. Muss ich nun alles von ihm explizit bestätigen, damit Du nicht glaubst, ich würde es ignorieren?

---

pluss schrieb:Darauf antwortete ich:

pluss schrieb:Aber eben nur bei Photonen, bzw. wenn ein Beobachter in seinem Inertialsystem etwas mit einer Geschwindigkeit von 1 c beobachtet. Dein obiger Satz gilt gerade nicht für Objekte mit einer Ruhemasse > 0. Abgesehen davon stünde das im Wiederspruch [sic !] der Verschiebungsinvarianz:

Wikipedia: Impulserhaltungssatz#Impulserhaltung als Folgerung der Homogenit.C3.A4t und Isotropie des Raumes

Nun ja, wieder eine falsche und unbelegte Behauptung von Dir, bei der Zeitdilatation und der Addition von Geschwindigkeiten und der Transformation von Geschwindigkeiten im Rahmen der SRT spielen Impulse keine Rolle, kannst Du ja auch im Internet bei Wikipedia nachlesen:

Wikipedia: Relativistisches Additionstheorem für Geschwindigkeiten

Im englischen Artikel:

Wikipedia: Velocity-addition formula#General configuration

steht es noch genauer, kann den aber als Grafik hier nicht mehr einbinden, lese es eben selber nach. Da steht auch nicht ein Wort über Impulse, da geht es nur um die Geschwindigkeiten.

Klingt seltsam, ist aber so ...

Ganz deutlich, das ist der Artikel zu Addition von Geschwindigkeiten im Rahmen der SRT, würden da Impulse eine Rolle spielen, oder die Reihenfolge in der die Geschwindigkeiten aufgebaut wurden, dann müsste es dort zu lesen sein. Da steht aber nichts. Du meinst echt, Du weißt es besser? Die Artikel auf Wikipedia sind also falsch?

---

pluss schrieb:Also @mojorisins als auch deine "Überzeugung" verstoßen gegen die Impuls- und Energieerhaltung. Und komme mir nicht wieder mit Beweislastumkehr. Du musst die Widersprüche entkräften, denn bei mir entstehen sie ja nicht.

[/quote]
Unfug, Du erfindest das einfach, Du behauptest, unsere Erklärungen würden gegen die Impuls- und Energieerhaltung verstoßen, tun sie aber nicht, belegst hast Du es auch nicht. Dein Link - so frei ohne jedes Zitat im Raum - belegt gar nichts. Wir haben es Dir vorgerechnet und verlinkt. Passt alles. Du stehst da mit Deiner Behauptung ganz alleine da. Und willst nun weiter ablenken, in dem Du mit Impulsen kommst. Die Größe irgendwelcher Impulse, wie auch die Reihenfolge der Beschleunigungen sind so irrelevant, wie die Farbe von Bobs und Alices Socken.

Klingt seltsam, ist aber so ...

pluss schrieb:

Wie der Impuls und die Energie eines Teilchens der Masse m in relativistischer Physik von der Geschwindigkeit v abhängen, folgt daraus, dass diese Größen für jeden Beobachter additive Erhaltungsgrößen sind. Da die Lagrangefunktion nicht vom Ort x abhängt, (das heißt, die Komponenten xi , i=1, 2, 3, sind zyklisch), ist die Wirkung invariant unter räumlichen Verschiebungen.

Hervorhebung (Unterstreichung) von mir.

Wikipedia: Relativistischer Impuls

Ja und? Du verstehst schon nicht, wie Geschwindigkeiten richtig im Rahmen der SRT transformiert werden, natürlich raffst Du dann auch nicht im Ansatz was ein relativistischer Impuls nun genau ist. Und eh schon sehr seltsam, man zeigt Dir immer und immer wieder die Artikel auf Wikipedia zum Thema, zitiert es über Monate immer und immer wieder, Du ignorierst es stur. Aber wenn Du glaubst, da auf Wikipedia was zu finden, was Dir ins Konzept passt und Deine Meinung stützt, dann geht es?

Nein Du, ...

Es geht hier um die Addition und Transformation von Geschwindigkeiten im Rahmen der SRT, nicht um Impulse. Es geht um die Zeitdilatation. Du solltest überall in der Fachliteratur nachlesen können, dass man dafür nichts über irgendwelche Impulse wissen muss.

Klingt seltsam, ist aber so ...

---

Dann noch eben zu:

pluss schrieb:Ein Einfaches ja hätte es auch getan, ...

Dann kommt von Dir nun ein einfaches ja oder nein zu der Frage an Dich mit den beiden Uhren von Bob? Du weißt schon noch, die beiden Rolex, Bob nimmt ja beide mit, eine startet er vor dem Start der Rakete und die andere danach. Nach Deinen Aussagen hier, sollte dann ja eine dilatiert laufen und die anderen nicht.

Und? Wie schaut es aus? Sagst Du da nun "Ja" zu?

nocheinPoet schrieb:Meine Aussage gibt genau das wieder, was man in der Fachliteratur zur SRT und der Zeitdilatation und der Addition und Transformation von Geschwindigkeiten lesen kann.

Nein, eben nicht:

Wikipedia: Lorentz transformation#Coordinate transformation

Ich werde hier nicht mehr ständig alles erneut zitieren. Anscheinend liest du es ja ohnehin nicht, oder verdrängst alles was im Widerspruch deiner Ansicht steht. Lese und vor allem verstehe den kurzen Artikel, oder lasse es.

@pluss

pluss schrieb:Nein, eben nicht:

Wikipedia: Lorentz transformation#Coordinate transformation

Ich werde hier nicht mehr ständig alles erneut zitieren. Anscheinend liest du es ja ohnehin nicht, oder verdrängst alles was im Widerspruch deiner Ansicht steht. Lese und vor allem verstehe den kurzen Artikel, oder lasse es.

Du, bisher hast Du nichts zitiert, aus dem man entnehmen könnte, dass der Impuls eine Rolle spielt, wir haben Dir hier hingegen immer wieder erklärt, zitiert, verlinkt und ganz oft im Detail vorgerechnet, wo Du irrst, was Du falsch machst, was Du nicht verstehst, was Du falsch verstehst.

Du bist es, der sich hier wieder um Antworten drückt, der auf die Rechnungen nicht weiter eingeht, der da keine Fehler aufzeigen kann, der nur stur einfach seine falschen Behauptungen wiederholt. Auch wenn diese frei im Raum schweben und widerlegt sind. Mehrfach widerlegt sind.

Du stehst hier doch ganz alleine, wer stimmt Dir bitte zu? Und wer widerspricht Dir?

Eben.

---

Noch mal ganz deutlich, da Du ja auf Wikipedia stehst, sogar in deutsch:

Die Komponenten der Geschwindigkeit u_⊥ (senkrecht zu v) sind zusätzlich um den Faktor γ ^-1 kleiner.

Wikipedia: Relativistisches Additionstheorem für Geschwindigkeiten#Definition

Eine Geschwindigkeit senkrecht zu v, kannst das echt nicht verstehen? Die Quelle ist doch auch wirklich ganz klar, das ist ein Artikel zum Relativistischen Additionstheorem für Geschwindigkeiten.

Also das passt doch wie Arsch auf Eimer. Da kannst Du die Definition nachlesen, darum steht da auch "Definition" drüber.

So, v ist die Geschwindigkeit zwischen beiden Systemen. Und u_⊥ ist die Geschwindigkeit, die senkrecht zu v steht. Und γ ist der Lorentzfaktor (LF) Gamma, der sich aus v eben errechnet.

---

Wurde Dir alles immer und immer wieder erklärt. Hier noch mal:

Transformation der Teilchengeschwindigkeit aus dem System S' in das System S:

γ = 1,667 (der Lorentzfaktor bei v = 0,8 c)

u'_⊥ = 0,6 c (Geschwindigkeit auf der y-Achse in S' - bekannt)
u_∥ = 0,8 c (Geschwindigkeit auf der x-Achse in S - bekannt)

u_⊥ = ??? c (Geschwindigkeit auf der y-Achse in S - gesucht)

u = (u_∥ ; u_⊥)
u = (u_∥ ; u'_⊥γ ^-1)
u = (u_∥ ; 0,6 c ⋅ 1,667 ^-1)
u = (0,8 c ; 0,3599 c)

So wird es richtig gerechnet, ohne Impuls und Beschleunigung, und das geht auch, wenn beide bekannten Geschwindigkeiten 0,9 c betragen, hatte ich Dir auch vorgerechnet. Und kannst Du da Fehler zeigen?

Nein kannst Du eben nicht. Darum gehst Du darauf auch nicht weiter ein, nein darum versucht Du mit Impulsen und anderen Schnickschnack abzulenken.

---

Und was ist denn nun hiermit:

pluss schrieb:

nocheinPoet schrieb:Er kann darauf nicht antworten, er findet keine Antwort, die das Paradoxon auflösen würde, den Widerspruch beseitigen. Da ist echt nun Ende im Gelände.

Mach dir da mal keine Sorgen, natürlich habe ich Antworten. Im Gegensatz zu dir sogar welche die im Einklang der Physik stehen. Aber heute habe ich kein Bock mehr auf deine Textwände.

Und wo sind denn nun Deine Antworten? Die Frage mit den beiden Uhren von Bob ist noch immer offen, so wie ich es vorhergesagt habe wird da nichts mit Substanz zu kommen, nein Du fabulierst lieber über Satelliten und Impulse und versucht abzulenken und Dich vor einer Antwort zu drücken.

Du stehst ja auch im Widerspruch zu dem was @mojorisin Dir erklärt, der ist aber eben Unisono mit meinen Aussagen und dem was auf Wikipedia steht.

Aber wie weiter von mir Vorhergesehen, wirst Du Dich nun zeitnahe ganz aus der Diskussion verabschieden, nichts neues eben ...

Und das ohne hier die offenen Fragen auch nur im Ansatz beantwortet zu haben.

nocheinPoet schrieb:Noch mal ganz deutlich, da Du ja auf Wikipedia stehst, sogar in deutsch:

   Die Komponenten der Geschwindigkeit u⊥ (senkrecht zu v) sind zusätzlich um den Faktor γ -1 kleiner.

Für dich auch nochmals:


Quelle: Wikipedia: Lorentz transformation#Vector transformations

@pluss

pluss schrieb:

nocheinPoet schrieb:Noch mal ganz deutlich, da Du ja auf Wikipedia stehst, sogar in deutsch:

Die Komponenten der Geschwindigkeit u_⊥ (senkrecht zu v) sind zusätzlich um den Faktor γ ^-1 kleiner.
[/color]

Für dich auch nochmals:

[/color]

Ach @pluss Du stellst Dir immer wieder ein neues Bein und rennst tiefer in den Nebel. Warum liest Du nicht mal was da steht und rechnest auch mal nach? Willst Du mich einfach bestätigen, wenn ich immer sage, Du verstehst die Artikel und Aussagen auf Wikipedia kein Stück?

Da steht nun doch ganz deutlich:

Only time and the coordinates parallel to the direction of relative motion change, while those coordinates perpendicular do not. With this in mind, split the spatial position vector r as measured in F, and r′ as measured in F′, each into components perpendicular (⊥) and parallel ( ‖ ) to v, ...

Wikipedia: Lorentz transformation#Vector transformations

Also r ist der position vector auf deutsch heißt das Ortsvektor. Die Rechnung zeigt also wie Längen aus dem System S' in das System S transformiert werden. Hättest Du Dir mal die Rechnung angeschaut, hättest Du auch darauf kommen sollen.

Schau doch mal genau hin, da steht vt also v ⋅ t, also eine Geschwindigkeit v mal einer Zeitdauer t. Da kommt dann eine Länge raus. Nun auch nicht schlecht, damit haben wir hier mal eben noch die Lorentzkontraktion angesprochen und gezeigt, diese findet nur parallel zum Geschwindigkeitsvektor statt.


System S' - Ruhesystem von Bob:

r'_⊥ = 0,3 Ls (y-Abstand zwischen den Reflektoren der Uhr)
r'_‖ = 0,0 Ls (x-Abstand zwischen den Reflektoren der Uhr)

Das ist eine Länge, keine Geschwindigkeit. Die Rechnung hier:

r_⊥ = r'_⊥

zeigt also nur, dass sich der Abstand auf der y-Achse nicht ändert, wenn beide Systeme zueinander auf der x-Achse bewegt sind. Also es gibt keine Lorentzkontraktion auf der y-Achse, wenn die Systeme zueinander auf der x-Achse bewegt sind. Aber es gibt eine Lorentzkontraktion auf der x-Achse, wenn man Deine Uhr auf die x-Achse kippen würde, ...

Soll ich Dir das auch noch mal genauer erklären und eventuell vorrechnen? Oder willst Du erst einmal mit dem Transformieren von Längen zwischen zwei zueinander bewegten Systemen im Rahmen der SRT selber üben?

@pluss

So ich bin wieder da. Leider nicht mit so viel Zeit wie ich gerne hätte. Hab schon gesehen, dass ihr euch weiter die Finger wund tippt. Aber die Zeit, um das alles zu lesen habe ich nicht. :-(

Daher werde ich da weitermachen, wo wir aufgehört haben, mich aber auf die Ur-Uhr konzentrieren. Je länger ich über das Konzept nachdenke, desto lehreicher finde ich das. Wir hatten:

ComCitCat schrieb am 22.09.2017:Erste Behauptung:
Eine Ur-Uhr dilatiert, wenn man sie erst auf der x-Achse auf 0,9 c beschleunigt und dann auf der y Achse auf 0,6c.
Sie dilatiert nicht, wenn man sie erst auf der y-Achse auf 0,6c beschleunigt, und dann auf der x-Achse auf 0,9c.

Sowie von dir:

pluss schrieb am 22.09.2017:Nicht ganz. Vorweg, aus Sicht von Bob bewegt sich die Kugel der Ur-Uhr auf der y-Achse mit 0,6c. Der Abstand der Detektoren beträgt 0,6Ls.

Wird die Rakete jetzt auf der x-Achse beschleunigt, dilatiert die Ur-Uhr nicht (weil die Kugel ihre Geschwindigkeitskomponente auf der y-Achse für andere Beobachter nicht verliert). Die Rakete kann jedoch nicht bis auf 0,9c auf der x-Achse beschleunigt werden, da sonst die resultierende Geschwindigkeit der Komponenten >c wäre. Es kann folglich theoretisch maximal (c2 - y2)0,5 auf der x-Achse an Geschwindigkeit erreicht werden.

Wird die Rakete zuerst gestartet und dann die Kugel der Ur-Uhr, dilatiert sie. Auch hier sollte der Grund auf der Hand liegen. Da Bob sich selbst mit seine Ur-Uhr als ruhend betrachtet, würde ein Kraftstoß (Impuls) seiner Kugel der Ur-Uhr, der in einem Ruhesystem zu einer Geschwindigkeit von 0,6c führt, für andere Beobachter eben nicht 0,6c erreichen können, da die Kugel durch die Bewegung auf der x-Achse (Rakete bewegt sich ja für andere Beobachter auf der x-Achse) schon eine dynamische Massenzunahme (relativistische Masse) besitzt. Der Impuls kann folglich nicht die gleiche Wirkung haben, wie er ihn hätte, wenn die Gesamtenergie der Kugel lediglich m0*c2 betragen würde.

Ich möchte jetzt erstmal so eine Ur-Uhr als Gedankenexperiment konstruieren. Ich würde sehr gerne mit Ladungen und Magnetfeldern arbeiten - für die Geschwindigkeiten scheint das passend. Aber beschleunigte Ladungsträger machen in der ART gewaltige Probleme. Sie strahlen nämlich so lange, bis sie "sich nicht mehr bewegen". Was immer das jetzt konkret heißen mag. :-D

Also machen wir es ohne Ladung im weitesten Sinn. Wir nehmen eine Kugel, und legen sie auf eine Kreisbahn, die wir fest in das Raumschiff von Bob integrieren, und die so konstruiert ist, dass keinerlei Reibung auftritt. Diese Kreisbahn soll senkrecht auf der X-Achse (sprich Antriebsachse) stehen, damit uns die Beschleunigung des Raumschiffs nicht irgendwelche Kräfte durcheinander bringt.

Kurz die Ur-Uhr [System 1] erläutert:
Wenn wir jetzt die Kugel mit 0,6 c anstubsen, dann vollführt sie eine Kreisbewegung mit einer im Betrag konstanten Beschleunigung und Geschwindigkeit (die stehen senkrecht aufeinander, und beide zusammen senkrecht auf der späteren Bewegungsrichtung des Raumschiffes). Nur die Richtung ändert sich. Das ist mir viel viel lieber, als zum Beispiel bei einer am "Spiegel" reflektierten Kugel irgendwelche Beschleunigungen rausrechnen zu müssen, die irre Probleme machen, weil sie entweder unendlich oder nicht gleichmäßig - also im Betrag auf der ganzen Bahn veränderlich sind.

SpoilerEine kleine Eigentümlichkeit, die mir hier wichtig ist: Wenn die Kugel sich mit 0,6c auf ihrer Bahn bewegt, dann ist gamma schon deutlich nicht mehr 1. Die Kugel dilatiert in der Zeit. Und ich bin mir nicht im klaren darüber, was das bedeutet. Von Bob aus gesehen (der ja im Raumschiff sitzt, auf dem die Kreisbahn montiert ist) hat die Kreisbahn einen Radius R und einen Umfang von 2 Pi x R. Von der Kugel ausgesehen ist der Umfang aber nur 2 Pi x R / Gamma (Längenkontraktion) - dadurch schafft die Kugel trotz Zeitdilatation einen vollen Umlauf in der Zeit, in der Bob das auch beobachtet. *grübel*
Ausgehend von der Äquivalenz von schwerer und träger Masse würde ich behaupten, dass die äußere Beschleunigung (von der Kreisbahn) genau den selben Effekt hat, wie eine ultraschwere Masse im Zentrum der Kreisbahn. Also quasi wenn die Kugel um einen Neutronenstern kreisen würde. Btw -das Problem betrifft nur die Eigenzeit der Kugel, nicht die Messung der Zeit der Ur-Uhr, weil wir da nur die Umläufe zählen und uns wurst ist, wie lange ein Umlauf jetzt genau gedauert hat.

Jetzt konstruiere ich eine alternative zweite Ur-Uhr [System 2]. Wir machen es im Prinzip genauso wie eben. Aber wir bauen in die Kugel einen Dauermagneten ein, und die Kreisbahn ist eine Transrapidstrecke. Auf diese Weise hat die Kugel der Ur-Uhr auf einmal einen Antrieb, und wir können sicherstellen, dass sie im System von Bob mit einer Geschwindigkeit von 0,6c auf ihrer Bahn unterwegs ist, und dass das auch so bleibt - egal was passiert. Als Ur-Uhr taugt sie dann natürlich nur noch bedingt, wir müssen ja die Geschwindigkeit der Kugel messen - und damit eine Unabhängige Uhr mitnehmen.

Und jetzt probieren wir mit den beiden verschiedenen 'Ur-Uhren' das Experiment. Wir beschleunigen Bobs Raumschiff gegenüber Alice auf einen Wert nahe 0,8c. Und die Frage die wir stellen ist diese: dilatiert die Ur-Uhr. Deine Aussage war:

pluss schrieb am 22.09.2017:Wird die Rakete jetzt auf der x-Achse beschleunigt, dilatiert die Ur-Uhr nicht (weil die Kugel ihre Geschwindigkeitskomponente auf der y-Achse für andere Beobachter nicht verliert). Die Rakete kann jedoch nicht bis auf 0,9c auf der x-Achse beschleunigt werden, da sonst die resultierende Geschwindigkeit der Komponenten >c wäre.[...]

Wird die Rakete zuerst gestartet und dann die Kugel der Ur-Uhr, dilatiert sie. Auch hier sollte der Grund auf der Hand liegen. Da Bob sich selbst mit seine Ur-Uhr als ruhend betrachtet, würde ein Kraftstoß (Impuls) seiner Kugel der Ur-Uhr, der in einem Ruhesystem zu einer Geschwindigkeit von 0,6c führt, für andere Beobachter eben nicht 0,6c erreichen können, da die Kugel durch die Bewegung auf der x-Achse (Rakete bewegt sich ja für andere Beobachter auf der x-Achse) schon eine dynamische Massenzunahme (relativistische Masse) besitzt. [...]

Okay. Nachdem was ich von dir verstanden habe, und was ich oben ein wenig abgedunkelt habe müsstest du folgenden Aussagen zustimmen:
1. Die Ur-Uhr [System 1] dilatiert nicht. denn wir haben sie erst angestoßen, und dann Bobs Raumschiff beschleunigt. Ergo gab es keine Kräfte in der y/z-Komponente, ergo kann sich am Lauf der Ur-Uhr nichts verändert haben.
2. Die Ur-Uhr [System 2] die wir ständig über ihren Antrieb nachkalibrieren dilatiert offensichtlich. Denn wir kalibrieren sie ja an einer Uhr, die Bob mitführt, und die selbstverständlich dilatiert. Wir kalibrieren sie aber immer so, dass sie im Ruhesystem von Bob auf der bekannten Kreisbahn mit 0,6c unterwegs ist.

Hier ergibt sich für dich ein eklatanter Widerspruch. Zur Erinnerung: Die Zeitmessung der Ur-Uhr funktioniert über das Zählen von Umläufen auf der Kreisbahn. Das die Ur-Uhr [1] nicht dilatiert, die Ur-Uhr [2] jedoch schon bedeutet für Bob, der ja die Bewegung der Uhr [2] überwacht und sicherstellt, dass sie in seinem eigenen Bezugssystem immer mit 0,6 c auf der selben Kreisbahn unterwegs ist, das die Ur-Uhr [1] bei der Beschleunigung entlang der x-Achse ihre Geschwindigkeit (die nur y und z-Komponenten aufweist) aus Sicht von Bob verändern muss (und zwar in diesen y- und z-Komponenten). Denn nur dann kann sich ein Laufzeitunterschied zur Uhr [2] ergeben. Ergo ergibt eine Beschleunigung streng entlang der X-Achse an irgendeiner Stelle zwangsläufig auch veränderungen auf der Y- und Z-Achse. :-)
SpoilerDas soll nicht heißen, dass bei einer gemeinsamen Beschleunigung auf der x-Achse sich im Ruhesystem von Bob die Geschwindigkeit der Ur-Uhr ändert. Ich würde instiktiv festlegen, dass im Ruhesystem von Bob alles beim alten bleiben muss, wenn wir alles (Raumschiff, Kreisbahn und Kugel) gleichmäßig auf der X-Achse beschleunigen. Mir geht es darum zu zeigen, dass deine Prämissen zwingend dazu führen, dass wir eine solche Änderung hinnehmen müssten. ;-)

So weit. Rechnungen sind mir persönlich egal, solange sie nicht nötig sind. Darum bin ich erstmal fertig. Kannst du das so nachvollziehen, oder habe ich irgendwo einen gedanklichen Fehler?

nocheinPoet schrieb:bisher hast Du nichts zitiert, aus dem man entnehmen könnte, dass der Impuls eine Rolle spielt

Doch schon, nur hast du es offensichtlich nicht gelesen. Was glaubst du denn wie Objekte zu Geschwindigkeiten kommen?
Weil Bibi Blocksberg hex hex sagt, oder weil sie einen Impuls erhalten haben?

Eben weil du meinst der Impuls spielt keine Rolle und du falsch rechnest, führt das dazu, das die Kugel der Ur-Uhr immer mehr an Geschwindigkeit verlieren würde, wenn Bobs Rakete nur oft genug mal positiv und mal negativ auf 0,8c auf der x-Achse beschleunigt wird. Nach 10 solchen Vorgängen hätte die Kugel nach "deiner Art des Rechnens" nur noch eine Geschwindigkeit von 0,01c auf der y-Achse. Nach 40 Vorgängen nur noch 0,4m/s und nach der 100sten Beschleunigung nur noch 1,96^-14m/s. Dass das im Widerspruch der Impulserhaltung steht kümmert dich nicht weiter. Warum auch, der Impuls spielt ja deiner überzeug nach keine Rolle in der SRT.

Löse erst mal den Widerspruch auf, bevor du deine Behauptungen immer nur wiederholst.

@ComCitCat, warum einfach, wenns auch kompliziert geht?

Also mir fehlt die Zeit um dein Gedankenexperiment durchzurechnen.

ComCitCat schrieb:Rechnungen sind mir persönlich egal, solange sie nicht nötig sind.

Die sind aber leider zwingend nötig, wie sonst willst du überprüfen ob deine Annahmen überhaupt im Einklang mit physikalischen Gesetzmäßigkeiten stehen?

ComCitCat schrieb:Von der Kugel ausgesehen ist der Umfang aber nur 2 Pi x R / Gamma (Längenkontraktion)

Das z.B. stimmt so meiner Erinnerung nach nicht. Der Radius bleibt für jeden Beobachter unverändert.

pluss schrieb:Das z.B. stimmt so meiner Erinnerung nach nicht. Der Radius bleibt für jeden Beobachter unverändert.

Deiner Erfahrung nach?? Im Gegensatz zum Interferenzexperiment nehme ich dir das hier nicht ab!

Du wirst meinen Text schon lesen müssen. Rechnen hingegen musst du praktisch nix. Ich habe das Gedankenexperiment, dass ja extra eine Anlehnung an deines ist, so angelegt, dass nur 2 Werte eine Rolle spielen. Istgleichnull und Istungleichnull. Mehr nicht. Da können wir uns die genauen Formeln der Längenkontraktion/Zeitdilatation/sonstiger Umrechnungsfaktoren erstmal schenken. Es geht ja auch nur darum, herauszufinden, ob deine Prämissen sinn machen, die ich dementsprechend konsequent eingesetzt habe - so wie von dir vorgegeben, so ich mich nicht vertan habe - um zu einem Widerspruch zu finden, der sie ad absurdum führt.

ComCitCat schrieb:wir bauen in die Kugel einen Dauermagneten ein, und die Kreisbahn ist eine Transrapidstrecke. Auf diese Weise hat die Kugel der Ur-Uhr auf einmal einen Antrieb, und wir können sicherstellen, dass sie im System von Bob mit einer Geschwindigkeit von 0,6c auf ihrer Bahn unterwegs ist, und dass das auch so bleibt - egal was passiert. Als Ur-Uhr taugt sie dann natürlich nur noch bedingt, wir müssen ja die Geschwindigkeit der Kugel messen - und damit eine Unabhängige Uhr mitnehmen.

Wie willst du messen?
Was hat man sich unter einer "Unabhängigen Uhr" vorzustellen?

ComCitCat schrieb:Deiner Erfahrung nach??

Nein, meiner Erinnerung nach. Oder ist dir etwas über Längenkontraktion bekannt, was rechtwinklig zur Geschwindigkeit steht? Dann würde ein Raumschiff ja nicht nur in der Länge, sondern auch in der breite (höhe) kontrahieren müssen.

pluss schrieb:Wie willst du messen?
Was hat man sich unter einer "Unabhängigen Uhr" vorzustellen?

Die Zeit die die Ur-Uhr anzeigt entspricht auf jeden Fall den gezählten Umläufen.
Eine Unabhängige Uhr ist eine ganz normal, die du im Raumschiff mitführst. Halt eine, die die Eigenzeit anzeigt.

pluss schrieb:Nein, meiner Erinnerung nach. Oder ist dir etwas über Längenkontraktion bekannt, was rechtwinklig zur Geschwindigkeit steht? Dann würde ein Raumschiff ja nicht nur in der Länge, sondern auch in der breite (höhe) kontrahieren müssen.

Das beantworte ich nicht selber. Hier kann mojorisin auf jeden Fall besser weiterhelfen als ich.

ComCitCat schrieb:Halt eine, die die Eigenzeit anzeigt.

Also eine Lichtuhr. Und mit dieser möchtest du messen ob sich die Geschwindigkeit der Kugel auf der Kreisbahn erhöht oder nicht?

pluss schrieb:Also eine Lichtuhr. Und mit dieser möchtest du messen ob sich die Geschwindigkeit der Kugel auf der Kreisbahn erhöht oder nicht?

Ich würde ja eine Absenkung erwarten, aber ja. Genau genommen will ich den Bewegungszustand der Ur-Uhr in Bobs Ruhesystem festhalten, so dass Bob vor und nach dem Beschleunigen die selbe Geschwindigkeit der Kugel der Ur-Uhr misst.

ComCitCat schrieb:Ich würde ja eine Absenkung erwarten, aber ja. Genau genommen will ich den Bewegungszustand der Ur-Uhr in Bobs Ruhesystem festhalten, so dass Bob vor und nach dem Beschleunigen die selbe Geschwindigkeit der Kugel der Ur-Uhr misst.

Ok, und das geht mit meinem Gedankenexperiment nicht?
Wo ist das Problem, Bob kann doch ebenfalls eine Lichtuhr mitführen.

pluss schrieb:Ok, und das geht mit meinem Gedankenexperiment nicht?
Wo ist das Problem, Bob kann doch ebenfalls eine Lichtuhr mitführen.

Doch, aber das ist nicht gut vergleichbar. Es geht doch darum:

ComCitCat schrieb:Hier ergibt sich für dich ein eklatanter Widerspruch. Zur Erinnerung: Die Zeitmessung der Ur-Uhr funktioniert über das Zählen von Umläufen auf der Kreisbahn. Das die Ur-Uhr [1] nicht dilatiert, die Ur-Uhr [2] jedoch schon bedeutet für Bob, der ja die Bewegung der Uhr [2] überwacht und sicherstellt, dass sie in seinem eigenen Bezugssystem immer mit 0,6 c auf der selben Kreisbahn unterwegs ist, das die Ur-Uhr [1] bei der Beschleunigung entlang der x-Achse ihre Geschwindigkeit (die nur y und z-Komponenten aufweist) aus Sicht von Bob verändern muss (und zwar in diesen y- und z-Komponenten). Denn nur dann kann sich ein Laufzeitunterschied zur Uhr [2] ergeben. Ergo ergibt eine Beschleunigung streng entlang der X-Achse an irgendeiner Stelle zwangsläufig auch veränderungen auf der Y- und Z-Achse. :-)

Und den Vergleich kannste mit ner Lichtuhr nicht machen.

ComCitCat schrieb:Hier ergibt sich für dich ein eklatanter Widerspruch. Zur Erinnerung: Die Zeitmessung der Ur-Uhr funktioniert über das Zählen von Umläufen auf der Kreisbahn. Das die Ur-Uhr [1] nicht dilatiert, die Ur-Uhr [2] jedoch schon bedeutet für Bob, der ja die Bewegung der Uhr [2] überwacht und sicherstellt, dass sie in seinem eigenen Bezugssystem immer mit 0,6 c auf der selben Kreisbahn unterwegs ist

Nein, das ist kein Widerspruch. Deine Uhr[2] kalibrierst du mit der mitgeführten Lichtuhr. Die Lichtuhr dilatiert, damit selbstverständlich auch deine "Unabhängige Uhr[2]". Welchen Sinn hat die Uhr[2] in deinem Gedankenexperiment, wenn sie exakt die Zeit einer Lichtuhr anzeigt?

Würde es nicht zur Verständlichkeit beitragen wenn Bob noch eine Sonnen- und eine Sanduhr dabei hätte?

pluss schrieb:Welchen Sinn hat die Uhr[2] in deinem Gedankenexperiment, wenn sie exakt die Zeit einer Lichtuhr anzeigt?

Sie überführt den abstrakten Zeitbegriff in konkrete physikalische Vorgänge, die gedanklich besser handhabar sind.
Deine Prämissen sagen,in dem einen Fall dilatiert die Ur-Uhr, in dem anderen Fall nicht.
Ich präsentiere 2 verschiedene Ur-Uhren, die diesen beiden Fällen entsprechen sollen. Ob sie das tun, ist der kritischste Punkt in meiner ganzen Argumentation. Wir setzten das im folgenden einfach vorraus, damit mein Argumentationschema klar wird.
Wir haben jetzt 2 Uhren, mit der gleichen physikalischen Wirkungsweise - sie messen Umläufe und setzen deren Zahl als Zeit an - eine dilatiert nach den Prämissen, die andere nicht.
Also müssen sich die physikalischen Wirkungen (nach den Prämissen) in den beiden Fällen unterscheiden. Und wir reden hier nicht von Kraftwirkungen durch das Beschleunigen, sondern von simpler Bewegung im Ruhesystem.
Wir haben aber in beiden Fällen die selbe Wirkung auf das System losgelassen - eine Beschleunigung in X-Richtung. Aber bekommen haben wir einmal eine Veränderung der Abläufe in der Y-Z-Ebene und einmal nicht. Ergo muss die Kraft in X-Richtung sehr wohl in der Lage sein, einfluss auf Y- und Z-Komponenten zu nehmen.

Wie der Einfluss dann aussieht ist nochmal ne ganz andere Frage.

ComCitCat schrieb:Ich präsentiere 2 verschiedene Ur-Uhren, die diesen beiden Fällen entsprechen sollen.

Ich auch, die Ur-Uhr und eine Lichtuhr. Oder kommst du mit einer Rotation der Kugel besser klar bei Berechnungen statt einer Bewegung auf der y-Achse?

ComCitCat schrieb:Ich präsentiere 2 verschiedene Ur-Uhren, die diesen beiden Fällen entsprechen sollen. Ob sie das tun, ist der kritischste Punkt in meiner ganzen Argumentation. Wir setzten das im folgenden einfach vorraus,

Das könnte ich bei meinem Gedankenexperiment auch einfach voraussetzen. Es geht hier ja aber um die Frage, steht das mit der Physik im Einklang.