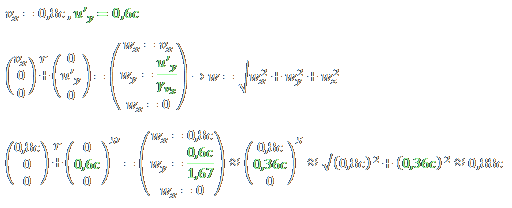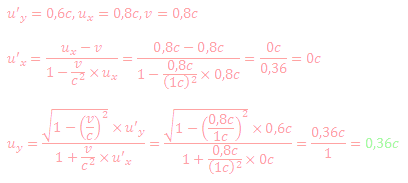Schwierigkeit der Längenkontraktion

Ok, ich muss da ein bisschen Nachdenken, wie ich da am besten drauf antworte. Fest steht, dass ich die Sachen anders rechne. Ich werd also versuchen, meinen Rechenweg zu zeigen, und zu erklären, warum ich so rechne. :-)

Allerdings wohl nicht mehr heute. Ich hab jetzt übrigens endlich dein Konzept einer Ur-Uhr verstanden. Glaube ich zumindest. :-D

ComCitCat schrieb:Ok, ich muss da ein bisschen Nachdenken, wie ich da am besten drauf antworte.

Ich habe mir fest vorgenommen 120 zu werden, also meinetwegen kannst du dir ruhig Zeit lassen. Ohnehin sind das dann in der Regel eher Beiträge mit Substanz als wenn man mal eben schnell aus der Hüfte auf der Tastatur rumhämmert.

ComCitCat schrieb:Ich hab jetzt übrigens endlich dein Konzept einer Ur-Uhr verstanden. Glaube ich zumindest. :-D

Das freut mich. Das ich kein begnadeter Erklärbar bin weiß ich wohl, allerdings kamen in mir schon erste Zweifel hoch, völlig unfähig darin zu sein, Sachverhalte wenigstens halbwegs verständlich rüberzubringen.

pluss schrieb:Weiters erkennt man, dass die Ur-Uhr nicht dilatiert.

Weil sie im Inertialsystem von ALice sitzt. Der zweiter Fall btrachtet die Geschwindigkeit des Raumschiffs in x-Richtung aus Sicht der Kugel.

Da die Lichtuhr aber eigentlich im Raumschiff sein sollte entspricht der zweite Fall nicht deinem Gedankenexperiment, sprich das Raumschiff vergisst glatt die Ur-Uhr mitzunehmen,

D.h. Die Kugel wird aus Sicht von ALice auf 0,6c beschleunigt. Während aus Sicht von Alice nun das Eaumschiff auf 0,8c beschleunigt, beschleunigt das Raumschiff auf der nunmehr mit 0,6c beschleungten Kugel nur auf 0,64c.

D.h. für Alice bewegt sich die Kugel ständig nur auf der y-Achse mit 0,6c und irgendwann fliegt das Raumschiff für AQlice in x-Richtung mit 0,8c davon. Aus SIcht der Kugel fliegt das Raumschiff auch davon aber nur mit eine x-Gschwidigkeit von 0,64c.

Die Geschwindigkeitsdifferenz zwischen Raumschiff und Kugel muss aber auf der x-Achse = 0.

mojorisin schrieb:Weil sie im Inertialsystem von ALice sitzt. Der zweiter Fall btrachtet die Geschwindigkeit des Raumschiffs in x-Richtung aus Sicht der Kugel.

Da die Lichtuhr aber eigentlich im Raumschiff sein sollte entspricht der zweite Fall nicht deinem Gedankenexperiment, sprich das Raumschiff vergisst glatt die Ur-Uhr mitzunehmen,

Sorry @mojorisin, aber es ist mir völlig unverständlich wie du zu dieser Interpretation gelangt bist.

Natürlich befindet sich die Ur-Uhr immer im Raumschiff von Bob. Sehe beim besten Willen auch nicht wo ich mich da derart missverständlich ausgedrückt haben sollte, zumal deine Interpretation ja auch vollkommen im Widerspruch meines Minkowski-Diagramms steht.

mojorisin schrieb:Die Geschwindigkeitsdifferenz zwischen Raumschiff und Kugel muss aber auf der x-Achse = 0.

Ist ja auch der Fall.

pluss schrieb:Sorry @mojorisin, aber es ist mir völlig unverständlich wie du zu dieser Interpretation gelangt bist.

Es ist keine Interpretation, es ist was du rechnest.

Die 0,6c nimmst du als Referenzgeschwindigkeit, und über die berechnest du die GEschwindigkeit des Raumschiffs. Das ist die GEschwindigkeit des Raumschiffes mit 0,8c aus Alices SIcht umgerechnet, in das System der Kugel die sich mit 0,6c relativ zu Alice bewegt.

@pluss

Von Wikipedia: Relativistisches Additionstheorem für Geschwindigkeiten:

Ein Beobachter B′ bewege sich gegenüber dem Beobachter B mit der Geschwindigkeit v

Dieser Beobachter B' beobachtget dann ein Objekt C mit der Geschwindigkeit u_x, u_y und u_z. Die Lorentztransformation hilft nun die Geschwindigkeiten die B' beobachtet so zu tranformieren das man weiß wie B sie wahrnimmt. Dies geschieht in dem man den Lorentzfaktor hernimmt der sich berechnet aus der Relativgeschwindigkeit v zwischen B und B'

Bei deinem Fall 1 ist Alice B, Bob in der Raktete ist B' und die Kugel das Objekt C.

Bei deinem Fall 2 ist Alice B, die Kugel ist B' und die Rakete das Objekt C.

Ich hoffe du erkennst den Unterschied.
Warum das so ist? Schau dir an zwischen welchen Objekten die GEschwindigkeit v stattfindet die du einsetzt um den Loretzfaktor auszurechnen.

--> Bei Fall 1 ist das die GEschwindigkeit 0,8c zwischen der Rakte und Alice.  
--> Bei Fall 2 ist das die Geschwindigkeit 0,6c zwischen dem Ball und Alice

Hab da mal eine Frage zwischendurch.
Nur für mein Verständnis und hat nicht direkt mit der aktuell beherrschenden Diskussion zu tun.

Also, verstehe ich es so grob richtig?:

Ich sehe Geschwindigkeiten im allgemeinen als relativ.
Es gibt also keinen festen Bezugspunkt aus dem man alle Geschwindigkeiten absolut bestimmen kann, oder nicht?
Als Beispiel:
Hier auf der Erde, an einem Bestimmten Ort auf einer sagen wir mal 1 km langen Strecke, messen wir die überwundene Strecke in einer bestimmten zurückgelegten Zeit, als x Geschwindigkeit.

Welche Geschwindigkeit würde man vom Saturn aus messen?
Und kann man die Lichtgeschwindigkeit eben drum als absolut bezeichnen? Wenn ja, kann man die LG denn als do. einen Bezugspunkt sehen?

Ich bitte also nur um kurze Aufklärung ob ich so in die richtige Richtung denke. Ich will gar nicht wissen mit welchen Formeln, Faktoren, Zahlen und Transformationen ich das feststellen kann, sind sich sowieso immer alle fachkundigen immer anschließend uneins drüber ^^
Ich möchte nur pauschal wissen, wieviel km/h, z.B. 100km/h, vom Saturn aus gemessen werden würde...bevor man es umrechnet in Erdverhältnisse und transformiert undwasweißich, damit wir auf dem Saturn wissen, wieviel km/h es für den Menschen auf der Erde ist.

Sind also alle Bezugssysteme im Universum, eigentlich alles eigene "Zeitrealitäten"?

Klingt vielleicht etwas OT, aber ich brauche das für mein Verständnis, um hier gedanklich themenbezogen weiterzukommen.

Nachtrag:
Kann die Frage auch sonst in einem anderen Thread verschieben, falls es hier jetzt unpässlich ist :-)

skagerak schrieb:Es gibt also keinen festen Bezugspunkt aus dem man alle Geschwindigkeiten absolut bestimmen kann, oder nicht?

Ja.

skagerak schrieb:Welche Geschwindigkeit würde man vom Saturn aus messen?

Ziemlich genau diesselbe. Aber nur weil die Relativgeschwindigkeit zwischen Erde und Saturn so gering ist im Vergleich zur LG. Das wäre anders wäre die Relativgeschwindigkeit zwischen Erde und Saturn viel näher an der LG, z.B. 0,8c.

skagerak schrieb:Und gilt die Lichtgeschwindigkeit eben drum als absolut bezeichnen?

Ja, in der SRT ist die LG absolut, d.h. egal welcher Beobachter alle messen in ihrem System die LG mit c. Man sagt c ist invariant, d.h. der Betrag der LG bleibt gleich, unter Koordinatentransformation.

skagerak schrieb:Sind also alle Bezugssysteme im Universum, eigentlich alles eigene "Zeitrealitäten"?

Ich glaube das könnte man so sagen.

@mojorisin
Okay, Danke :-) das hat mir schon sehr geholfen.

Nur hier noch mal'ne Frage:

Ziemlich genau diesselbe. Aber nur weil die Relativgeschwindigkeit zwischen Erde und Saturn so gering ist im Vergleich zur LG. Das wäre anders wäre die Relativgeschwindigkeit zwischen Erde und Saturn viel näher an der LG, z.B. 0,8c.

Okay, aber mal abgesehen von der geringen Relativgeschwindigkeit zwischen Erde und Saturn, ist doch Fakt, dass es einen Unterschied geben müsste, oder nicht?

Natürlich setze ich hier ja eben voraus, dass wir in diesem Gedanken mal den Saturn als Bezugspunkt nehmen. Okay, hier fängt es an schwierig zu werden für mich. Wir können doch eben nur aus unserer Sicht (aka "unserer Zeitrealität") alles betrachten, also auch keine realistische Aussage aus Sicht des Saturn machen, oder? Eben nur auf Basis der SRT alles auf uns bezogen betrachten?

Nachtrag: und eben deswegen kann man alles mit nichts vergleichen, weil eben alles relativ ist. Sagt das die ART und/oder SRT?

skagerak schrieb:Nachtrag: und eben deswegen kann man alles mit nichts vergleichen, weil eben alles relativ ist. Sagt das die ART und/oder SRT?

So wie ich das verstehe nicht, Du brauchst nur die richtigen Formeln um die Verhältnisse auszurechnen. Problem ist halt, dass es der eigenen Vorstellungswelt nicht entspricht.

@Balthasar70
Okay, das nähert mich schon denke ich.
Verhältnisse ist hier für mich das richtige Stichwort.
Wir, mit unseren Erd-Verhältnissen, sind also auch nicht die Referenz und ausschlaggebend für die Relativtät?
Wenn ja, denn kann ich es auch differenzieren, also wirklich relativ als relativ verstehen.

Nachtrag:
Das verwirrt mich auch jetzt selber sehr.
Also dient die Relativität auch nur unserem Verständnis und der praktischen Anwendung?

@skagerak
Für Dein Leben ist diese Relativität komplett wurscht. :-)

ComCitCat schrieb:Ok, ich muss da ein bisschen Nachdenken, wie ich da am besten drauf antworte. Fest steht, dass ich die Sachen anders rechne. Ich werd also versuchen, meinen Rechenweg zu zeigen, und zu erklären, warum ich so rechne. :-)

Wie schon angemerkt ist alles gerechne hier für die Katz, da hier ständig die Bezugssysteme durcheinander gebracht werden. Wer kann hier was messen ist erstmal entscheidend. Der Fehler beginnt ganz am Anfang, noch bevor überhaupt gerechnet wird.

skagerak schrieb:Ich sehe Geschwindigkeiten im allgemeinen als relativ.
Es gibt also keinen festen Bezugspunkt aus dem man alle Geschwindigkeiten absolut bestimmen kann, oder nicht?

In der SRT ist das so. In der ART und in der Praxis ist das schwerer zu beantworten. Es scheint ausgezeichnete Bezugssysteme zu geben. Die allgemeine Auflösung des Zwillingsparadoxons legt das theoretisch nahe, und praktisch gibt es auch ein paar Anhaltspunkte. Das ist aber Gegenstand intensiver sowohl physikalischer als auch philosophischer als auch metaphysischer Spekulationen. Wobei das Dogma der herrschenden Leere die Frage einfach bejahen würde. :-D

skagerak schrieb:Und kann man die Lichtgeschwindigkeit eben drum als absolut bezeichnen? Wenn ja, kann man die LG denn als do. einen Bezugspunkt sehen?

Man kann die Lichtgeschwindigkeit als absolut bezeichnen. Und das Dogma der herrschenden Lehre tut das auch. Wenn man genauer hinschaut bleibt, dass die Lichtgeschwindigkeit auf jeden Fall endlich ist, aber frappierender Weise Phänomene im Zusammenhang damit manchmal so tun als sei sie unendlich. Obwohl sie nen endlichen Wert hat.

Beispiel:
Wenn auf der Sonne ein Photon emmitiert wird, dann braucht das zu uns 8 Minuten, und kommt dann irgendwo an, wo es absorbiert wird (damit du es beobachten kannst). Aus Sicht dieses Photons jedoch vergeht keine Zeit. Es wird zum selben Zeitpunkt von der Sonne emmitiert und irgendwo auf der Erde absorbiert. Fairer Weise muss man dazu sagen, dass das Photon auch glaubt, dass beides am selben Ort passiert...

Nebenbei gibt es Physiker die sich fragen, ob der Wert der Lichtgeschwindigkeit wirklich unveränderlich ist. Aber das ist wieder so eine Frage wilder spekulationen. Ich will damit nur darauf ansprechen, das uns vieles im Rahmen der SRT und der ART nicht ganz so klar und unumstritten ist, wie die herrschende Lehre immer tut... ;-)

skagerak schrieb:Sind also alle Bezugssysteme im Universum, eigentlich alles eigene "Zeitrealitäten"?

Auch hier wieder... die dogmatische Lehrmeinung sagt ganz klar JA. Aber dann machen sie seltsame Sachen, wie zum Beispiel dem Universum ein Alter und EINE Geschichte zuzuschreiben. Was ja wohl offensichtlich nicht dazu passt.

Der Hintergrund ist der, dass es an jedem Ort Bezugssysteme mit einer bestimmten Geschwindigkeit zu geben scheint, die sozusagen minimal ist. Also im Bezugssystem mit dieser Geschwindigkeit an diesem Ort hat das Universum eine maximale Größe - mit jeder anderen Geschwindigkeit sieht alles irgendwie kleiner aus. Sprich näher zusammen gerückt. Und es scheint wohl so zu sein, dass man diese Geschwindigkeit bestimmen kann, indem man die kosmische Hintergrundstrahlung beobachtet. Wenn die aus allen Richtungen mit der gleichen Temperatur auf dich einstrahlt, dann hast du so etwas wie eine kosmische Nullpunktsgeschwindigkeit erreicht.
Dazu muss man anmerken, dass es da Differenzen gibt, die ein wenig Cracy aussehen. Denn wenn du die kosmische Hintergrundstrahlung hier beobachtest, und diese 0-Geschwindigkeit bestimmst, und das selbe dann in der Andromeda-Galaxie machst, dann kommst du dahin, dass diese beiden Geschwindigkeiten nicht gleich sind - zwei Körper die an diesen beiden Orten jeweils diese Null-Geschwindigkeit haben würden sich voneinander wegbewegen (allerdings noch nicht viel/schnell). In der herrschenden Lehre wird das ganze - so seltsam es ist - mit nur einem Satz umschrieben:
Das Universum dehnt sich aus.

Sorry, weiß nicht ob das zur klärung beiträgt. Aber vielleicht hilft es ja dabei weitere Fragen zu formulieren... *pfeifteinliedchen*

@ComCitCat
Danke, ja, das hat mir schon sehr geholfen. :-)

mojorisin schrieb:Bei deinem Fall 1 ist Alice B, Bob in der Raktete ist B' und die Kugel das Objekt C.

Bei deinem Fall 2 ist Alice B, die Kugel ist B' und die Rakete das Objekt C.

Nein, eben nicht.
Alice ist S (B) und die Kugel der Ur-Uhr ist S‘ (B‘). Die vektorielle Darstellung betrachtet ausschließlich die Kugel.


@mojorisin, ich versuche nochmals deinen Denkfehler aufzuzeigen.
Wenn deine Art der Berechnung zur Bestimmung der Geschwindigkeit auf der y-Achse so korrekt sein sollte, führt es zu folgenden Paradoxien:

Ein Satellit mit vier Steuerdüsen (je eine oben, unten, links, rechts) beschleunigt mit seiner oberen Steuerdüse den Satelliten auf eine Geschwindigkeit von 0,6c auf der y-Achse.

Frage: Wie kann der Satellit auf 0,3c auf der y-Achse abgebremst werden?

Meine Antwort wäre: Nur durch eine negative Beschleunigung auf der y-Achse. Durchführbar über die untere Steuerdüse.

Deine Antwort (logische Schlussfolgerung deiner Art der Berechnung) müsste in etwa so lauten: Über eine der Seitlichen (links, rechts) Steuerdüsen. Dafür muss der Satellit nur auf der x-Achse auf 0,87c beschleunigen, negativ (über die rechte) oder positiv (über die linke Steuerdüse). Oder durch eine negative Beschleunigung auf der y-Achse über die untere Steuerdüse.

Kommt dir das nicht "merkwürdig" vor, zumal man durch abwechselnde Beschleunigungen (positive, negative) auf der x-Achse dann eine Geschwindigkeit auf der y-Achse von 0 erzielen könnte?

Noch paradoxer wird es, wenn man die Gesamtenergie des Systems berechnet. Die Energie der ersten Beschleunigung plus der Energie der zweiten Beschleunigung ergibt die Gesamtenergie des Systems. Bei meiner Art der Berechnung besteht weder ein Widerspruch der Impuls- noch der Energieerhaltung. Darstellbar über den relativistischen Pythagoras (Energie-Impuls-Dreieck).

Bei deiner Art der Berechnung geht Energie spurlos verloren, was nicht der Fall sein darf, wenn deine Art der Berechnung korrekt wäre.
Wie gedenkst du diese Widersprüche zu entkräften?

@ComCitCat | @skagerak

ComCitCat schrieb:

skagerak schrieb:Ich sehe Geschwindigkeiten im allgemeinen als relativ. Es gibt also keinen festen Bezugspunkt aus dem man alle Geschwindigkeiten absolut bestimmen kann, oder nicht?

In der SRT ist das so. In der ART und in der Praxis ist das schwerer zu beantworten. Es scheint ausgezeichnete Bezugssysteme zu geben. Die allgemeine Auflösung des Zwillingsparadoxons legt das theoretisch nahe, und praktisch gibt es auch ein paar Anhaltspunkte. Das ist aber Gegenstand intensiver sowohl physikalischer als auch philosophischer als auch metaphysischer Spekulationen. Wobei das Dogma der herrschenden Leere die Frage einfach bejahen würde.

Es scheint ausgezeichnete Bezugsysteme zugeben? Wohl weniger und weder die "allgemeine Auflösung" des Zwillingsparadoxon noch eine andere "Auflösung" legen das nahe. Weder theoretisch noch praktisch, aber wenn Du das glaubst, warum nennst Du da nicht mal die Anhaltspunkte? Und warst Du es nicht, der neulich noch selber erklärte, er verstehe das Paradoxon mit den Zwillingen gar nicht?

ComCitCat schrieb:Nebenbei gibt es Physiker die sich fragen, ob der Wert der Lichtgeschwindigkeit wirklich unveränderlich ist. Aber das ist wieder so eine Frage wilder Spekulationen. Ich will damit nur darauf ansprechen, das uns vieles im Rahmen der SRT und der ART nicht ganz so klar und unumstritten ist, wie die herrschende Lehre immer tut...

Ja, es wird schon hinterfragt, wie konstant die Naturkonstanten sind, geht dabei nicht nur um die Lichtgeschwindigkeit, zu bedenken ist aber, alle diese Konstanten sind so unglaublich fein abgestimmt, wird da nur an einer wo was geändert, und sei es auch über 10 Stellen nach dem Komma fliegt und das Universum um die Ohren. Dann können die Atome sich nicht so aufbauen, wie sie es tun, oder die Sterne eben nicht "funktionieren". Neben der Lichtgeschwindigkeit grübelt man da auch über die Feinstrukturkonstante.

Mich hätte ja nun mal interessiert, wie Du da die Dinge "rechnest" die @pluss servierte ...

nocheinPoet schrieb:Mich hätte ja nun mal interessiert, wie Du da die Dinge "rechnest" die @pluss servierte ...

Das ist nicht ganz so einfach. Unter anderem versuche ich die Ur-Uhr in eine Form zu bringen, die uns die leidigen Geschwindigkeiten <0,6c am Umkehrpunkt erspart. Ich denke mal das geht, indem man die Kugel aufner Kreisbahn um die x-Achse rotieren lässt. Aber dann muss man eben nicht nur rechnen, sondern auch noch Gedankenexperimente finden, die zeigen, warum man so rechnen muss, und nicht anders. pluss hat ja in seinem letzten Beitrag schon wieder sehr schön dargelegt, warum er der Meinung ist, so rechnen zu müssen. Ich finde das Satellitenbeispiel auch schön eingängig. :-)
Mich jetzt hinzusetzen, und zu sagen, dass es aber anders gerechnet werden müsste, ohne erklären zu können warum, wäre ein bisschen billig oder? ;-)

nocheinPoet schrieb:Es scheint ausgezeichnete Bezugsysteme zugeben? Wohl weniger und weder die "allgemeine Auflösung" des Zwillingsparadoxon noch eine andere "Auflösung" legen das nahe. Weder theoretisch noch praktisch, aber wenn Du das glaubst, warum nennst Du da nicht mal die Anhaltspunkte?

Hab ich. Da:

ComCitCat schrieb:Der Hintergrund ist der, dass es an jedem Ort Bezugssysteme mit einer bestimmten Geschwindigkeit zu geben scheint, die sozusagen minimal ist. Also im Bezugssystem mit dieser Geschwindigkeit an diesem Ort hat das Universum eine maximale Größe - mit jeder anderen Geschwindigkeit sieht alles irgendwie kleiner aus. Sprich näher zusammen gerückt. Und es scheint wohl so zu sein, dass man diese Geschwindigkeit bestimmen kann, indem man die kosmische Hintergrundstrahlung beobachtet. Wenn die aus allen Richtungen mit der gleichen Temperatur auf dich einstrahlt, dann hast du so etwas wie eine kosmische Nullpunktsgeschwindigkeit erreicht.

Im Nachgang ist der Hinweis auf die Größe des Univesums ein wenig gewagt. Besser ist zu sagen, dass in diesem System am meißten Eigenzeit im Vergleich zu allen dazu bewegten Bezugssystemen vergeht. Du kommst um so eine Betrachtung kaum herum, wenn du entscheiden möchtest, welcher Zwilling der ältere ist. Zu sagen, das liege an den Beschleunigungen ist witzlos. Und feige.

@McMurdo

McMurdo schrieb:Wie schon angemerkt ist alles Gerechne hier für die Katz, da hier ständig die Bezugssysteme durcheinander gebracht werden. Wer kann hier was messen ist erstmal entscheidend. Der Fehler beginnt ganz am Anfang, noch bevor überhaupt gerechnet wird.

Ja, stimme Dir da zu, aber gibt doch auch einen Erfolg zu verbuchen, @pluss hat nun endlich verstanden, wo die beiden Geschwindigkeiten gemessen werden. Musste ja nur ganz oft viele Tage immer und immer wieder erklärt werden und schon schwuppsdiwupps kam es im Hirn an und zog auch ein. Nun betont er es selber ganz deutlich:

pluss schrieb:Die erste Beschleunigung (der Rakete von Bob) findet auf der x-Achse statt, welche zu einer Geschwindigkeit von 0,8 c führt. Die zweite Beschleunigung (der Kugel der Ur-Uhr in der Rakete von Bob) findet auf der y'-Achse statt, die zu einer Geschwindigkeit auf der y'-Achse von 0,6 c führt.

Da freut man sich doch wirklich, wenn man gehört wird, es aufgegriffen wird und umgesetzt. Sehr schön, ein Schritt weiter. Wie ich ja @pluss ganz oft schrieb und erklärte, schaut es so aus:

System S' - Ruhesystem von Bob:

u'_x = 0,0 c (Teilchen in der Uhr)
u'_y = 0,6 c (Teilchen in der Uhr)


System S - Ruhesystem von Alice:

u_x = 0,8 c (Rakete von Bob und Teilchen in der Uhr)
u_y = ??? c (Teilchen in der Uhr)

---

Gut, nun haben wir da jetzt 0,8 c zwischen Bob un Alice, der Wert selber ist ja aber nicht entscheidend. Auch die Rechnung schaut recht passabel aus, etwas überladen:



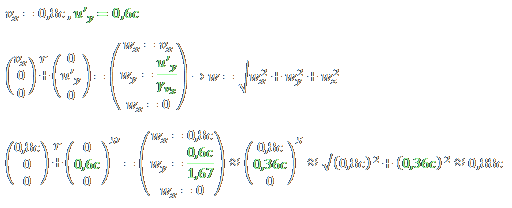
Aber immerhin stimmen die Werte. Inzwischen wird auch einfach der Lorentzfaktor (LF) Gamma vorab ausgerechnet und dann eingesetzt. Macht es schon übersichtlicher. Wenn man schaut, was das vorher für ein Monster war:



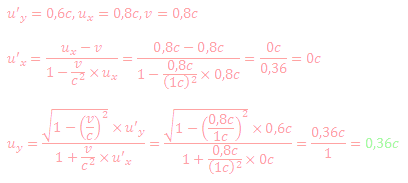
nur um da auf:

u_y = 0,36 c

zu kommen. Und dann meinte er selber ja noch, die Rechnung tauge nicht für sein Beispiel und hat die deshalb extra rot eingefärbt gehabt. Aber Schnee von Gestern, wir sind ja nun darüber dann doch hinausgekommen.

---

Man muss aber nicht noch die Komponenten für die z-Achse mitschleppen und könnte auch statt Spalten-Vektoren Zeilen-Vektoren nehmen.

System S - Ruhesystem von Alice:

u = (u_x ; u_y)
u = (u_x ; u'_yγ ^-1)

Spaltenvektor sind schon schön und auch "besser" aber so braucht man kein LATEX und kann besser zitieren, also reiner Pragmatismus und solange man keine Matrizen multipliziert geht es eben auch so.

Kennt man also nun den Lorentzfaktor (LF) Gamma γ, hat den also vorab richtig berechnet, schaut es ganz einfach und übersichtlich aus, die Geschwindigkeit welche Alice in S für das Teilchen auf der y-Achse misst berechnet sich dann so:

γ = 1,667 (der Lorentzfaktor bei 0,8 c)

u_y = u'_y ⋅ γ ^-1
u_y = 0,6 c ⋅ 1,667 ^-1
u_y = 0,3599 c

Also gerundet eben u_y = 0,36 c die 0,36 c welche auch @pluss da nun stehen hat. Sehr schön, geht doch weiter, langsam aber es geht.


Ich wiederhole mal hier abschließen für den Absatz die Rechnung.

System S - Ruhesystem von Alice:

u_x = 0,8 c (Rakete von Bob und Teilchen in der Uhr)
u_y = ??? c (Teilchen in der Uhr)

u = (u_x ; u_y)
u = (u_x ; u'_yγ ^-1)
u = (u_x ; 0,6 c ⋅ 1,667 ^-1)
u = (0,8 c ; 0,3599 c)

Damit sind dann beide Geschwindigkeitskomponenten im System S von Alice für die Kugel oder das Teilchen bekannt und können mit dem Pythagoras dann addiert werden. Machen wir dann später ... ;)

---

Nun geht es dann weiter zum nächsten Schritt, leider hat sich @pluss ja gleich wieder ein neues Bein gestellt. @mojorisin hat es ja ganz deutlich angesprochen und aufgezeigt, ich hänge mich da einfach mal an. Eventuell schafft man es ja gemeinsam in ein paar Tagen auch diesen Baum vom Weg zu räumen.

Wichtig ist natürlich nun, den Lorentzfaktor (LF) Gamma vorab richtig zu berechnen. Dafür braucht man die Geschwindigkeiten zwischen den Beiden Systemen, zwischen denen man Größen transformieren möchte. Wir haben das System S' von Bob und das System S von Alice und wir kennen die Geschwindigkeit zwischen beiden:

u_x = 0,8 c (System S' von Bob, Bob eben mit seiner Rakete)

Das System S' von Bob bewegt sich von Alice in S aus gemessen mit 0,8 c auf der x-Achse. Ergibt sich aus der Geschwindigkeit der Rakete von Bob, denn Bob ruht ja mit Uhr in seiner Rakete. Wie sich Gamma γ nun berechnet wurde hier im Thread schon ganz oft gezeigt, und da diese Rechnung selber nicht bestritten wird, reicht hier nun auch einfach ein Link auf eine Tabelle für einige Werte von γ abhängig eben von v:

https://www.lernhelfer.de/schuelerlexikon/physik-abitur/artikel/lorentz-transformation

Nicht wundern, γ wird dort als k-Faktor bezeichnet. Wie wir dort nun der Tabelle entnehmen können, beträgt bei einer Geschwindigkeit zwischen den System von 0,8 c:

γ = 1,667

Und damit muss dann auch gerechnet werden. Wer nun für γ = 1,250 einsetzt, der nimmt v = 0,6 c und diese Geschwindigkeit gibt es zwischen den Systemen von Bob und Alice in dem Beispiel hier nicht. Das ist ja die Geschwindigkeit, welche Bob in seinem System S' für die Kugel auf der y-Achse misst.

Und somit hat @mojorisin recht, wenn er @pluss darauf hinweißt, dass dieser sich da verhaspelt und nun in das Ruhesystem der Kugel transformiert. Das sollte man dann mit S'' bezeichnen. Aber ganz sicher brauchen wir hier nun nicht noch ein weiteres System.

Also, nächster Meilenstein hier ist, den Lorentzfaktor (LF) Gamma γ = 1,667 bei einer Geschwindigkeit von v = 0,8 c zwischen dem System S' von Bob und dem System S von Alice fest zu etablieren und verständlich zu machen, dass v = 0,6 c zur Berechnung des Faktors falsch ist.  

@pluss

pluss schrieb:Alice ist S (B) und die Kugel der Ur-Uhr ist S‘ (B‘).

Nein, das System in dem Alice ruht, also das Ruhesystem von Alice ist S. Und das System in dem Bob mit seiner Rakete und Uhr ruht, also das Ruhesystem von Bob ist S'. Die Kugel ist doch nun im System S' von Bob auf der y-Achse bewegt:

System S' - Ruhesystem von Bob:

u'_x = 0,0 c (Teilchen in der Uhr)
u'_y = 0,6 c (Teilchen in der Uhr)


Auch wenn es hier sicher nur noch mehr Unruhe bringt, für die Kugel eben.

System S'' - Ruhesystem der Kugel:

u''_x = 0,0 c (Kugel in der Uhr)
u''_y = 0,6 c (Kugel in der Uhr)

u''_x = 0,0 c (Rakete von Bob, wenn Bob die Uhr nicht aus dem Fenster wirft ...)
u''_y = 0,6 c (Rakete von Bob)

u''_x = ??? c (Alice)
u''_y = 0,6 c (Alice)

Für die Geschwindigkeiten von Alice in S'' muss ich mir noch kurz Gedanken machen, kommt dann nachgereicht. Will da auf die Schnelle nichts falsches hinschreiben. Gut, denke u''_y = 0,6 c passt, muss aber dennoch noch mal drüber grübeln. u''_x müsste man dann wohl mit der LT berechnen. @mojorisin ist da offenbar schon weiter als ich.


Aber, wie gesagt, Du selber hast erklärt:

pluss schrieb am 20.09.2017:Man man man @nocheinPoet, Alice sitzt faul in ihrem Sessel und beobachtet wie Bob in seiner Rakete durch die Weiten des Alls düst, und dabei wie blöde die ganze Zeit auf seine Ur-Uhr starrt. Alice sitzt und saß in diesem Gedankenexperiment nie in einer Rakete. Unabhängig davon kann sich natürlich jeder als ruhend betrachten. Aber wie schon klar und deutlich aus dem Gedankenexperiment hervorgeht, interessiert hier nur und ausschließlich was Alice beobachtet.

Also warum nun das:

pluss schrieb:Die vektorielle Darstellung betrachtet ausschließlich die Kugel.

Warum willst Du nun in das Ruhesystem der Kugel wechseln? Noch nicht genug Baustellen offen? Noch mehr Verwirrung stiften? Bedenke, im System S'' der Kugel ruht die Kugel und die Uhr mit Bob und seiner Rakete sind dann auf der y-Achse mit 0,6 c bewegt. Denn die Kugel bewegt sich von beiden ja auf der y-Achse weg, also hin und her, somit bewegen die beiden sich aus dem System der Kugel betrachtet auch auf der y-Achse hin und her.

Und dann sollte Alice eine weiter Geschwindigkeit auf der x-Achse erhalten. Es macht einfach nicht wirklich Sinn, sich das alles noch mal aus dem Ruhesystem der Kugel durch den Kopf zu drücken, mag ja interessant sein, aber dann doch bitte erst, wenn die anderen Baustellen beendet wurden.