Schwierigkeit der Längenkontraktion
Schwierigkeit der Längenkontraktion
04.10.2017 um 21:36Durch die Äquivalenz von Energie und Masse kann man Photonen eine Masse verpassen. Eine Ruhemasse ist das nicht.ComCitCat schrieb:Der Witz ist halt, genau das kommt im Prinzip auch raus, wenn man es trotzdem mal ausprobiert...
Durch eine falsche Annahme kommt man auch mal zum richtigen Ergebnis, sinnig ist das nicht.
Schwierigkeit der Längenkontraktion
04.10.2017 um 21:41Ich sprach auch nicht von Ruhemasse sondern Ruhesystem. Und ich gebe gerne zu, dass ich mich da blöd ausgedrückt habe. Besser ist, ein Bezugssystem das sich mit Lichtgeschwindigkeit von der Photonenemission zur Photonenabsorbtion bewegt. Und konsistent mit euren Argumenten verschwindet in diesem Bezugssystem das Photon. (auch eine Begründung, warum "Ruhesystem" ziemlich sinnlos ist)totte schrieb:Eine Ruhemasse ist das nicht.
Schwierigkeit der Längenkontraktion
04.10.2017 um 21:51@pluss
299.792.458 m/s = c
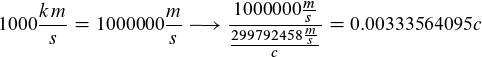

Wenn das Argument stimmt warum können wir dann trotz unserer Geschwindigkeit von über 1000 km/s gegenüber dem VirgoHaufen Protonen, die nach weislich eine Ruhemasse haben auf über 0,999999991c beschleunigen? Dennpluss schrieb:Nein. Er kann beschleunigen und auch unabhängig vom Photon an Geschwindigkeit gewinnen. Warum: Weil Photonen keine Ruhemasse besitzen.
299.792.458 m/s = c
Schwierigkeit der Längenkontraktion
04.10.2017 um 21:54Es gibt kein Bezugssystem mit der Geschwindikeit c.ComCitCat schrieb:Ich sprach auch nicht von Ruhemasse sondern Ruhesystem. Und ich gebe gerne zu, dass ich mich da blöd ausgedrückt habe. Besser ist, ein Bezugssystem das sich mit Lichtgeschwindigkeit von der Photonenemission zur Photonenabsorbtion bewegt. Und konsistent mit euren Argumenten verschwindet in diesem Bezugssystem das Photon. (auch eine Begründung, warum "Ruhesystem" ziemlich sinnlos ist)
melden
Schwierigkeit der Längenkontraktion
04.10.2017 um 21:57Schwierigkeit der Längenkontraktion
04.10.2017 um 22:03Und warum nicht? Das ein Photon kein Ruhesystem haben kann ist klar, aber warum sollte man ihm kein Bezugssystem zuordnen?totte schrieb:Es gibt kein Bezugssystem mit der Geschwindikeit c.
Schwierigkeit der Längenkontraktion
04.10.2017 um 22:24@totte
Im richtigen Leben, wenn man in ein Gespräch reinplatzt, ist es hilfreich sich erst ein paar Sätze der Leute anzuhören um deren Argumention zu verstehen bevor man seinen Senf dazu gibt. Hier im Forum ist es noch einfacher, da man einfach etwas zurückblättern kann, um sich die Gesprächsgeschichte anzuschauen. Auf jeden Fall hilft das Vorgehen, um zu verhindern völlig planlos einen Kommentar zu einer Aussage abzudrücken, ohne den Gesamtzusammenhang dieser Aussage zu verstehen.totte schrieb:Und jetzt nur noch das Ganze relativistisch richtig berechnen, dann stimmt es auch.
nocheinPoet

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2006
dabei seit 2006
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Schwierigkeit der Längenkontraktion
05.10.2017 um 12:46@intruder
Gleichzeitig, gleiche Zeit, es geht hier um etwas das verglichen wird, gleich sein kann und einen Wert hat, hier konkret um die Zeit. In der Physik haben Ereignisse Koordinaten, wir fragen, hat sich das "gleichzeitig" ereignet. Wenn man schon "Jemand" braucht, dann stellt der sich eben diese Frage, haben da zwei Ereignisse gleiche Zeitkoordinaten? Haben sie sich gleichzeitig ereignet?
Nehmen wir Anstelle von gleichzeitig mal gleichhöhig, gegeben sind zwei Turmuhren, beide Türme 100 m hoch und sie stehen 1.000 m auf der x-Achse auseinander.
Nun fragen wir mal, sind beide Türme "gleichhöhig"?
Eben, klar sind sie es. Auch hier wird nach gleichen Werten von Koordinaten gefragt, die Höhe ist beides mal 100 m auf der y-Achse.
Nun kann sich ein "Jemand" nahe vor den ersten Turm stellen und auf den zweiten blicken, der erste ist für ihn 200 m entfernt, der andere 1.200 m. Der in der Ferne sieht nun "kleiner" aus, mit den Augen sieht "Jemand" nun unterschiedliche Höhen für beide Türme, aber würde er deswegen sagen, sie sind nicht gleichhöhig?
In der Physik spielt der Ort des "Jemand" - oft auch Beobachter genannt - keine Rolle für den Wert der "beobachtet" wird. Und "beobachten" steht in der Regel als "Synonym" für "Messen" und hier sind Koordinaten und physikalische Größen gefragt.
Noch mal ein Vergleich Zeitkoordinaten und Ortskoordinate, "Jemand" sieht den Blitz einer Supernova, die ist mal zum Glück 8.000 Lichtjahre von uns entfernt. Sie hat sich also vor 8.000 Jahren ereignet, auch wenn uns das Licht erst jetzt erreicht.
Fragt "Jemand" nun nach der Zeit des "Ereignisses" werden die 8.000 Jahre Lichtlaufzeit von dem Zeitpunkt der "Beobachtung" abgezogen. Ist nun ganz wichtig, auch wieder, man darf nicht den Zeitpunkt des Ereignisses mit dem der Messung verwechseln.
Generell wird immer nach dem Zeitpunkt des Ereignisses gefragt, selten nur nach dem Zeitpunkt der Messung.
Nun "beobachtet" Jemand die Supernova, das macht er auf der Erde, also die Ortskoordinaten der Messung sind die der Erde, aber eben nicht die des Ereignisses. So wie man nach den Ortskoordinaten eines Ereignisses fragt und die vergleicht, fragt man auch nach den Zeitkoordinaten des Ereignisses. Man fragt nicht nach den Koordinaten der Messung und vergleicht diese. Also in der Regel zumindest eben nicht, man vergleicht die Zeitkoordinaten der Ereignisse auf "Gleichzeitigkeit".
Merken wir uns:
1. Es werden Koordinatenwerte von Ereignissen verglichen
2. Der Messort und Messzeitpunkt ist nicht das gemessene Ereignis
Noch mal zu den beiden Turmuhren, zwischen beiden in der Mitte haben wir eine Atomuhr die über zwei Laserstrahlen jede Sekunde einen Blitz zu den beiden Uhren schickt. Die Uhren dort "kennen" den Abstand zur Uhr, die Lichtlaufzeit und stellen so die Uhren eben auf die "richtige" Zeit. Beide Uhren laufen so also synchron. Tun sie, für jeden zur Atomuhr und den Türmen ruhenden "Beobachter". Nun schlagen zwei Blitze in beide Turmuhren, beide bleiben daraufhin sofort stehen. Beide zeigen 12:00:00 Uhr, auf die Nanosekunde genau.
Die Frage hier, sind beide Blitze nun "gleichzeitig" eingeschlagen? Die Antwort ist jetzt recht klar, ja sind sie, beide Uhren zeigen ja gleiche Zeiten der Einschlag-Ereignisses an.
Klar kann man nun einen "Jemand" dicht neben einer Turmuhr stellen, der "sieht" dann den Lichtblitz des anderen Einschlages in der anderen Turmuhr eben etwas später, weil das Licht ein wenig Zeit für den Weg braucht. Er "sieht" dann die Einschläge nicht "gleichzeitig", aber er "beobachtet" sie in seinem Ruhesystem dennoch gleichzeig. Denn auch hier ist Beobachtungszeitpunkt nicht Ereigniszeitpunkt.
In der Physik bedeutet also: "Alice beobachtet zwei Blitzeinschläge gleichzeitig" - da gibt es ein Ruhesystem und in diesem sind die Zeitkoordinaten zwei Ereignisse gleich. Wo Alice da nun auch steht, und ob sie es überhaupt tut, ist irrelevant.
Wichtig ist mehr, ob der fiktive "Beobachter" ruht. Nun verstehst man unter "jeder Andere" einfach andere Bezugsysteme. Wir haben hier im Thread immer das Ruhesystem von Alice S und das Ruhesystem von Bob B'. Beide sind zueinander bewegt. Fragen wir nun, was "sieht" Alice, ist auch wieder nur nach Werten in dem Ruhesystem von Alice gefragt.
Wichtig, Du kannst nun fiktiv beliebig viele "Jemande" in ein Ruhesystem stellen, wenn einer da was "gleichzeitig" bezeichnet, dann ist es für alle dort gleichzeitig.
Merken wir uns:
1. Wo "wer" in einem System steht, ist für die Frage nach der Gleichzeitigkeit nicht entscheidend
2. Entscheidend ist, ob sich sein Ruhesystem gegenüber einem anderen System bewegt.
Wir haben nun das Ruhesystem von Alice, dort fallen nun Deine beiden Bälle "gleichzeitig" zu Boden. Dann ereignet sich das für alle "Beobachter" gleichzeitig, die zu Alice ruhen. Deutlicher, in allen anderen Systemen, die zum Ruhesystem von Alice ruhen ereignen sich beide Ereignisse auch gleichzeitig.
Noch mal zu den beiden Turmuhren, wo wir hier schon ein Beispiel formuliert haben, wenn Bob nun mit seinem System auf der x-Achse mit 0,9 c zwischen den beiden Türmen unterwegs ist, dann misst er beide Einschläge real nicht gleichzeitig.
Wichtig, für Bob, in seinem System finden beide Ereignisse wirklich nicht gleichzeitig statt, hat nichts mit Lichtlaufzeiten in dem Sinne zu tun. Natürlich wird auch Bob da zwei kaputte Uhren finden, beide stehen auf 12:00 Uhr, aber für Bob gehen beide Uhren nicht synchron, sie zeigen für Bob nicht gleichzeitig gleiche Zeiten an.
Warum das so ist, erklärt sich dann über die Relativität der Gleichzeitigkeit, dazu dann aber mal was in einem anderen Beitrag, wenn Interesse besteht.
Nur noch mal zu der "Erklärung" von @Peter0167 hier:
Kann für Einige dann doch zu Irritationen führen. Darum ist auch die erste Antwort von @Zotteltier hier richtig:
Gut, ich gehe mal davon aus, so wie Du fragst und erklärst, Du liest hier mit, dass es hier auch im den Kontext geht, spielt gleich eine wichtige Rolle.intruder schrieb:Mal allgemein für mich, wenn es nicht stört. Ich versuche in Rahmen meiner Möglichkeiten hier mitzulesen um daher kurz eine Frage, ob ich halbwegs auf dem Stand bin.
Hier ging es um die Relativität der Gleichzeitigkeit, ich vermute um das "gleichzeitig" geht es Dir, so wie es da in der Physik, konkret der SRT verstanden wird. Gibt nämlich immer mal wen, der versteht "gleichzeitig" doch etwas anders und erklärt es dann auch so, und dabei kommt dann nichts wirklich Gutes raus, denn er macht nicht deutlich, dass er es eben etwas anders versteht und seine Antwort nicht in den Rahmen der SRT passt.intruder schrieb:Es gibt 2 Ereignisse die jemand als gleichzeitig wahrnimmt.
Gleichzeitig, gleiche Zeit, es geht hier um etwas das verglichen wird, gleich sein kann und einen Wert hat, hier konkret um die Zeit. In der Physik haben Ereignisse Koordinaten, wir fragen, hat sich das "gleichzeitig" ereignet. Wenn man schon "Jemand" braucht, dann stellt der sich eben diese Frage, haben da zwei Ereignisse gleiche Zeitkoordinaten? Haben sie sich gleichzeitig ereignet?
Nehmen wir Anstelle von gleichzeitig mal gleichhöhig, gegeben sind zwei Turmuhren, beide Türme 100 m hoch und sie stehen 1.000 m auf der x-Achse auseinander.
Nun fragen wir mal, sind beide Türme "gleichhöhig"?
Eben, klar sind sie es. Auch hier wird nach gleichen Werten von Koordinaten gefragt, die Höhe ist beides mal 100 m auf der y-Achse.
Nun kann sich ein "Jemand" nahe vor den ersten Turm stellen und auf den zweiten blicken, der erste ist für ihn 200 m entfernt, der andere 1.200 m. Der in der Ferne sieht nun "kleiner" aus, mit den Augen sieht "Jemand" nun unterschiedliche Höhen für beide Türme, aber würde er deswegen sagen, sie sind nicht gleichhöhig?
In der Physik spielt der Ort des "Jemand" - oft auch Beobachter genannt - keine Rolle für den Wert der "beobachtet" wird. Und "beobachten" steht in der Regel als "Synonym" für "Messen" und hier sind Koordinaten und physikalische Größen gefragt.
Noch mal ein Vergleich Zeitkoordinaten und Ortskoordinate, "Jemand" sieht den Blitz einer Supernova, die ist mal zum Glück 8.000 Lichtjahre von uns entfernt. Sie hat sich also vor 8.000 Jahren ereignet, auch wenn uns das Licht erst jetzt erreicht.
Fragt "Jemand" nun nach der Zeit des "Ereignisses" werden die 8.000 Jahre Lichtlaufzeit von dem Zeitpunkt der "Beobachtung" abgezogen. Ist nun ganz wichtig, auch wieder, man darf nicht den Zeitpunkt des Ereignisses mit dem der Messung verwechseln.
Generell wird immer nach dem Zeitpunkt des Ereignisses gefragt, selten nur nach dem Zeitpunkt der Messung.
Nun "beobachtet" Jemand die Supernova, das macht er auf der Erde, also die Ortskoordinaten der Messung sind die der Erde, aber eben nicht die des Ereignisses. So wie man nach den Ortskoordinaten eines Ereignisses fragt und die vergleicht, fragt man auch nach den Zeitkoordinaten des Ereignisses. Man fragt nicht nach den Koordinaten der Messung und vergleicht diese. Also in der Regel zumindest eben nicht, man vergleicht die Zeitkoordinaten der Ereignisse auf "Gleichzeitigkeit".
Merken wir uns:
1. Es werden Koordinatenwerte von Ereignissen verglichen
2. Der Messort und Messzeitpunkt ist nicht das gemessene Ereignis
Noch mal zu den beiden Turmuhren, zwischen beiden in der Mitte haben wir eine Atomuhr die über zwei Laserstrahlen jede Sekunde einen Blitz zu den beiden Uhren schickt. Die Uhren dort "kennen" den Abstand zur Uhr, die Lichtlaufzeit und stellen so die Uhren eben auf die "richtige" Zeit. Beide Uhren laufen so also synchron. Tun sie, für jeden zur Atomuhr und den Türmen ruhenden "Beobachter". Nun schlagen zwei Blitze in beide Turmuhren, beide bleiben daraufhin sofort stehen. Beide zeigen 12:00:00 Uhr, auf die Nanosekunde genau.
Die Frage hier, sind beide Blitze nun "gleichzeitig" eingeschlagen? Die Antwort ist jetzt recht klar, ja sind sie, beide Uhren zeigen ja gleiche Zeiten der Einschlag-Ereignisses an.
Klar kann man nun einen "Jemand" dicht neben einer Turmuhr stellen, der "sieht" dann den Lichtblitz des anderen Einschlages in der anderen Turmuhr eben etwas später, weil das Licht ein wenig Zeit für den Weg braucht. Er "sieht" dann die Einschläge nicht "gleichzeitig", aber er "beobachtet" sie in seinem Ruhesystem dennoch gleichzeig. Denn auch hier ist Beobachtungszeitpunkt nicht Ereigniszeitpunkt.
Da haben wir es wieder, eigentlich spielst Du keine echte Rolle, in der Physik ist mit "beobachten" in der Regel "messen" gemeint, wie schon erklärt, werden hier Koordinaten gemessen und physikalische Größen. Unter "Beobachter" wird in der Physik auch in der Regel einfach nur ein "System" verstanden, da muss nicht wirkliche "Jemand" an einem "Ort" stehen und mit den Augen was "sehen" oder anders "beobachten".intruder schrieb:Ich stelle mir hier 2 Bälle vor, die auf den Boden auftreffen. Wenn ich das Ereignis als gleichzeitig wahrnehme, muss jeder andere auch das Ereignis als gleichzeitig wahrnehmen, wenn auch nicht gleichzeitig mit mir.
In der Physik bedeutet also: "Alice beobachtet zwei Blitzeinschläge gleichzeitig" - da gibt es ein Ruhesystem und in diesem sind die Zeitkoordinaten zwei Ereignisse gleich. Wo Alice da nun auch steht, und ob sie es überhaupt tut, ist irrelevant.
Wichtig ist mehr, ob der fiktive "Beobachter" ruht. Nun verstehst man unter "jeder Andere" einfach andere Bezugsysteme. Wir haben hier im Thread immer das Ruhesystem von Alice S und das Ruhesystem von Bob B'. Beide sind zueinander bewegt. Fragen wir nun, was "sieht" Alice, ist auch wieder nur nach Werten in dem Ruhesystem von Alice gefragt.
Wichtig, Du kannst nun fiktiv beliebig viele "Jemande" in ein Ruhesystem stellen, wenn einer da was "gleichzeitig" bezeichnet, dann ist es für alle dort gleichzeitig.
Merken wir uns:
1. Wo "wer" in einem System steht, ist für die Frage nach der Gleichzeitigkeit nicht entscheidend
2. Entscheidend ist, ob sich sein Ruhesystem gegenüber einem anderen System bewegt.
Wir haben nun das Ruhesystem von Alice, dort fallen nun Deine beiden Bälle "gleichzeitig" zu Boden. Dann ereignet sich das für alle "Beobachter" gleichzeitig, die zu Alice ruhen. Deutlicher, in allen anderen Systemen, die zum Ruhesystem von Alice ruhen ereignen sich beide Ereignisse auch gleichzeitig.
Schau an, Du hast es doch selber richtig gewusst. Ja, die Information des Auftreffen auf dem Boden ist entscheiden und gefragt. Nicht wann wer wo vom Licht des Ereignisses erreicht wird.intruder schrieb:Angenommen jemand würde sich mit c von dem Ereignis entfernen, der würde natürlich nie das Ereignis wahrnehmen, und jemand der entsprechen weit weg von der Ereignis ist, würde es entsprechend später wahrnehmen, aber immer noch gleichzeitig. Welche Geschwindigkeit die Bälle haben spielt dafür keine Rolle, da nur der Zeitpunkt entscheidend ist, in dem die Information über das Auftreffen auf dem Boden entsteht.
Noch mal zu den beiden Turmuhren, wo wir hier schon ein Beispiel formuliert haben, wenn Bob nun mit seinem System auf der x-Achse mit 0,9 c zwischen den beiden Türmen unterwegs ist, dann misst er beide Einschläge real nicht gleichzeitig.
Wichtig, für Bob, in seinem System finden beide Ereignisse wirklich nicht gleichzeitig statt, hat nichts mit Lichtlaufzeiten in dem Sinne zu tun. Natürlich wird auch Bob da zwei kaputte Uhren finden, beide stehen auf 12:00 Uhr, aber für Bob gehen beide Uhren nicht synchron, sie zeigen für Bob nicht gleichzeitig gleiche Zeiten an.
Warum das so ist, erklärt sich dann über die Relativität der Gleichzeitigkeit, dazu dann aber mal was in einem anderen Beitrag, wenn Interesse besteht.
Nur noch mal zu der "Erklärung" von @Peter0167 hier:
Peter "sieht" die Dinge etwas anders, er versteht sie anders, er versteht hier mit "Ereignis wahrnehmen" wirklich, wann ein realer Beobachter mit seinen Sinnen das Ereignis misst, nicht aber, wann sich das Ereignis wirklich ereignet hat.Peter0167 schrieb:Nicht unbedingt, hängt vom Standort des Beobachters ab. Wenn du genau in der Mitte zwischen 2 Bällen stehst, die auf den Boden fallen, und du nimmst beide Ereignisse gleichzeitig wahr, würde ein anderer Beobachter, der sich in deinem Ruhesystem befindet, unter Umständen etwas anderes wahrnehmen, und zwar genau dann, wenn die Bälle zu ihm unterschiedliche Abstände haben. Dann trifft die Info des Balles, der sich näher am 2. Beobachter befindet vor der Info des entfernteren Balles ein (immer unter der Grundannahme, dass Beobachter 1 beide Ereignisse gleichzeitig wahrnimmt, und er genau in der Mitte zwischen den Bällen steht). (m.M.n.)
Kann für Einige dann doch zu Irritationen führen. Darum ist auch die erste Antwort von @Zotteltier hier richtig:
Wie Du siehst, er klärt es es so wie ich und so wie Du es selber ja schon beschrieben hast. Dabei solltest Du auch bleiben und Dich nicht verwirren lassen.Zotteltier schrieb:Zwei zueinander ruhende Beobachter können aber Lichtlaufzeiten berechnen, und stimmen dann darin überein ob zwei Ereignisse gleichzeitig waren oder nicht. Ein bewegter Beobachter kommt auf gleichem Wege dazu, dass die Ereignisse nicht gleichzeitig sind.
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:29@Peter0167
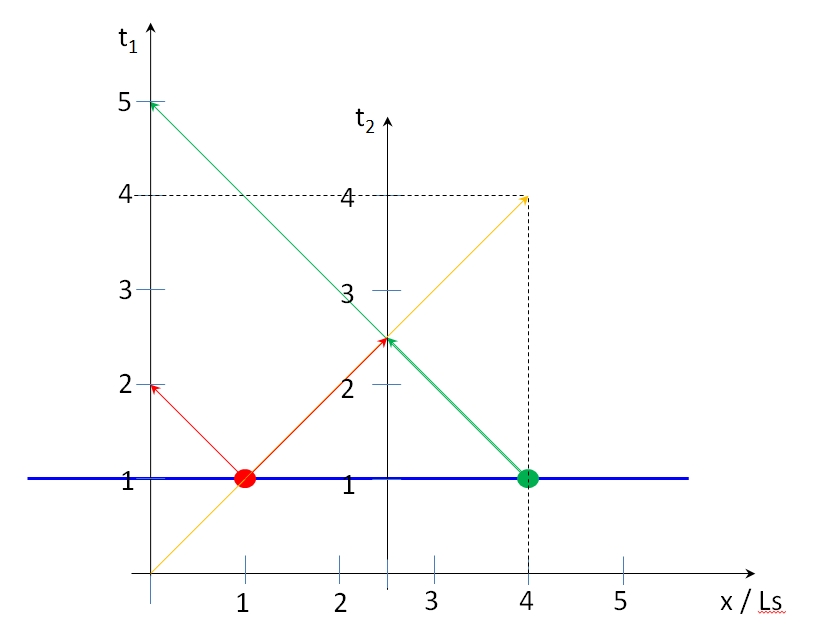
Der rote Ball und der blaue Ball schlagen bei folgenden Positionen auf der x-Achse auf: rot bei 1Ls grün bei 4Ls.
Aus Sicht eines Beobachter "2" der sich auf der x-Position = 2,5 Ls befindet, also mittig von den zwei Bällen, empfängt die Signale des Aufschlages gleichzeitig auf siner Zeitachse bei 2,5s und er sieht das die beiden Bälle "gleichzeitig bei 1s" aufgesprungen sind.
Ein Beobachter "1" der nun zu "Beobachter 2" ruht aber an einer andere x-Stelle nämlich bei x = 0 Ls, sieht die INdormationen der Bälle bei 2 s (rot) und 5 s (grün). Aufgrund der Luichtlaufzeiten finden die Aufschläge auch bei diesem Beobachter bei t = 1s sowie bei x = 1Ls (rot) und x = 4Ls (grün) statt. Beide Ereignisse sind verschiedenortig und gleichzeitig aus Sicht beider Beobachter, was auch logisch ist da sie zueinander ruhen (siehe blaue Linie) Das Erreichen der information des Vorganges ist natürlich unterschiedlich.
Warum ist die strenge Betrachtung so wichtig? Gleichzeitige Vorgänge können niemals kausal also voneinander abhängig sein, das eine Vorgang wegen der Lichtlaufzeit, erst etwas Zeit braucht um auf einen anderen Vorgang einzuwirken.
Auch wenn Beobachter 1 nun das Aufhüpfen der Bälle versetzt wahrnimmt, ist für ihn klar das die Vorgägen nicht kausal sein können, da sie, auch wenn die Info zeitlicvh versetzt ankommt, gleichzeitig passiert sind.
Unterschiedliche zeitliche und örtliche Bewertungen von Ereignissen können nur dann zustandekommen wenn sich zwei Beobachter zueineder bewegen.
Diese Aussage ist tasächlich falsch. Warum will ich kurz an dem Diagramm zeigen:Peter0167 schrieb:Frage: wenn Beobachter 1 die Ereignisse gleichzeitig wahrnimmt, nimmt sie Beobachter 2 dann auch gleichzeitig wahr?
Antwort: Es ist abhängig von der Konstellation

Der rote Ball und der blaue Ball schlagen bei folgenden Positionen auf der x-Achse auf: rot bei 1Ls grün bei 4Ls.
Aus Sicht eines Beobachter "2" der sich auf der x-Position = 2,5 Ls befindet, also mittig von den zwei Bällen, empfängt die Signale des Aufschlages gleichzeitig auf siner Zeitachse bei 2,5s und er sieht das die beiden Bälle "gleichzeitig bei 1s" aufgesprungen sind.
Ein Beobachter "1" der nun zu "Beobachter 2" ruht aber an einer andere x-Stelle nämlich bei x = 0 Ls, sieht die INdormationen der Bälle bei 2 s (rot) und 5 s (grün). Aufgrund der Luichtlaufzeiten finden die Aufschläge auch bei diesem Beobachter bei t = 1s sowie bei x = 1Ls (rot) und x = 4Ls (grün) statt. Beide Ereignisse sind verschiedenortig und gleichzeitig aus Sicht beider Beobachter, was auch logisch ist da sie zueinander ruhen (siehe blaue Linie) Das Erreichen der information des Vorganges ist natürlich unterschiedlich.
Warum ist die strenge Betrachtung so wichtig? Gleichzeitige Vorgänge können niemals kausal also voneinander abhängig sein, das eine Vorgang wegen der Lichtlaufzeit, erst etwas Zeit braucht um auf einen anderen Vorgang einzuwirken.
Auch wenn Beobachter 1 nun das Aufhüpfen der Bälle versetzt wahrnimmt, ist für ihn klar das die Vorgägen nicht kausal sein können, da sie, auch wenn die Info zeitlicvh versetzt ankommt, gleichzeitig passiert sind.
Unterschiedliche zeitliche und örtliche Bewertungen von Ereignissen können nur dann zustandekommen wenn sich zwei Beobachter zueineder bewegen.
nocheinPoet

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2006
dabei seit 2006
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:30@pluss
1. Lichtuhr:
v = 0,9 c (Geschwindigkeit zwischen beiden Systemen)
γ = (√ (1 - v²)) -1 = 2,294 (der Lorentzfaktor bei 0,9 c)
u'y = 1,0 c (Photon in der Uhr)
ux = 0,9 c (Rakete von Bob und Teilchen in der Uhr)
uy = ??? c (y-Geschwindigkeit des Photon in der Uhr im System S von Alice)
...
2. Kugeluhr, vor der Rakete gestartet:
v = 0,9 c (Geschwindigkeit zwischen beiden Systemen)
γ = (√ (1 - v²)) -1 = 2,294 (der Lorentzfaktor bei 0,9 c)
u'y = 0,6 c (Teilchen in der Uhr)
ux = 0,9 c (Rakete von Bob und Teilchen in der Uhr)
uy = ??? c (y-Geschwindigkeit des Teilchen in der Uhr im System S von Alice)
...
3. Kugeluhr, nach der Rakete gestartet:
v = 0,9 c (Geschwindigkeit zwischen beiden Systemen)
γ = (√ (1 - v²)) -1 = 2,294 (der Lorentzfaktor bei 0,9 c)
u'y = 0,6 c (Teilchen in der Uhr)
ux = 0,9 c (Rakete von Bob und Teilchen in der Uhr)
uy = ??? c (y-Geschwindigkeit des Teilchen in der Uhr im System S von Alice)
...
So, ganz wichtig ist eben hier, wie Du jeweils für jede Uhr den Lorentzfaktor Gamma γ = (√ (1 - v²)) -1 berechnest, der beträgt bei einer Geschwindigkeit von v = 0,9 c zwischen beiden Systemen eben immer 2,294.
Und daran hältst Du Dich in Deinen Rechnungen nicht, wo Du Fehler machst und wie die genau aussehen, hat Dir doch @mojorisin ganz genau hier:
Beitrag von mojorisin (Seite 38)
erklärt und aufgezeigt, soll ich das auch noch einmal im Detail machen? Damit Du es dann auch wieder ignoriert und nicht verstehst?
@totte
Hier findest Du eine kleine Zusammenfassung, @mojorisin kann ganz sicher richtig relativistisch Rechnen, er nahm sich hier nur den "Rechenweg" von @pluss um dem wieder mal seine Fehler deutlich vor Augen zu führen.
Beitrag von nocheinPoet (Seite 32)
Ist da wohl das erste Mal, und auch da ist nicht sauber beschrieben, welche Uhr nun gerade "berechnet" wird. Sollte in etwas so ausschauen:pluss schrieb:
Wie oft soll ich sie denn noch posten?nocheinPoet schrieb:Was ist mit den Rechnungen für die drei Uhren?
Beitrag von pluss (Seite 37)
1. Lichtuhr:
v = 0,9 c (Geschwindigkeit zwischen beiden Systemen)
γ = (√ (1 - v²)) -1 = 2,294 (der Lorentzfaktor bei 0,9 c)
u'y = 1,0 c (Photon in der Uhr)
ux = 0,9 c (Rakete von Bob und Teilchen in der Uhr)
uy = ??? c (y-Geschwindigkeit des Photon in der Uhr im System S von Alice)
...
2. Kugeluhr, vor der Rakete gestartet:
v = 0,9 c (Geschwindigkeit zwischen beiden Systemen)
γ = (√ (1 - v²)) -1 = 2,294 (der Lorentzfaktor bei 0,9 c)
u'y = 0,6 c (Teilchen in der Uhr)
ux = 0,9 c (Rakete von Bob und Teilchen in der Uhr)
uy = ??? c (y-Geschwindigkeit des Teilchen in der Uhr im System S von Alice)
...
3. Kugeluhr, nach der Rakete gestartet:
v = 0,9 c (Geschwindigkeit zwischen beiden Systemen)
γ = (√ (1 - v²)) -1 = 2,294 (der Lorentzfaktor bei 0,9 c)
u'y = 0,6 c (Teilchen in der Uhr)
ux = 0,9 c (Rakete von Bob und Teilchen in der Uhr)
uy = ??? c (y-Geschwindigkeit des Teilchen in der Uhr im System S von Alice)
...
So, ganz wichtig ist eben hier, wie Du jeweils für jede Uhr den Lorentzfaktor Gamma γ = (√ (1 - v²)) -1 berechnest, der beträgt bei einer Geschwindigkeit von v = 0,9 c zwischen beiden Systemen eben immer 2,294.
Und daran hältst Du Dich in Deinen Rechnungen nicht, wo Du Fehler machst und wie die genau aussehen, hat Dir doch @mojorisin ganz genau hier:
Beitrag von mojorisin (Seite 38)
erklärt und aufgezeigt, soll ich das auch noch einmal im Detail machen? Damit Du es dann auch wieder ignoriert und nicht verstehst?
@totte
Hier findest Du eine kleine Zusammenfassung, @mojorisin kann ganz sicher richtig relativistisch Rechnen, er nahm sich hier nur den "Rechenweg" von @pluss um dem wieder mal seine Fehler deutlich vor Augen zu führen.
Beitrag von nocheinPoet (Seite 32)
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:40Moin moin @mojorisin
Alles schön und gut, aber es ging in der Frage niemals darum ob die Ereignisse gleichzeitig geschehen, sondern ausschließlich um die Wahrnehmung von Gleichzeitigkeit bei unterschiedlichen Beobachtern im gleichen Ruhesystem!
Hier noch mal der unveränderte Originaltext:
Alles schön und gut, aber es ging in der Frage niemals darum ob die Ereignisse gleichzeitig geschehen, sondern ausschließlich um die Wahrnehmung von Gleichzeitigkeit bei unterschiedlichen Beobachtern im gleichen Ruhesystem!
Hier noch mal der unveränderte Originaltext:
Ginge es um die Frage nach der Gleichzeitigkeit beider Ereignisse, dann trifft das zu was du sagst, geht es aber nicht, da nach der Wahrnehmung gefragt wurde.intruder schrieb:Es gibt 2 Ereignisse die jemand als gleichzeitig wahrnimmt. Ich stelle mir hier 2 Bälle vor, die auf den Boden auftreffen. Wenn ich das Ereignis als gleichzeitig wahrnehme, muss jeder andere auch das Ereignis als gleichzeitig wahrnehmen, wenn auch nicht gleichzeitig mit mir.
nocheinPoet

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2006
dabei seit 2006
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:46@mojorisin
Du, @Peter0167 versteht unter "gleichzeitig wahrnehmen" nicht das, was in der Physik üblich damit gemeint ist. Habe ihm das auch schon mal erklärt, vergeblich:
Du, @Peter0167 versteht unter "gleichzeitig wahrnehmen" nicht das, was in der Physik üblich damit gemeint ist. Habe ihm das auch schon mal erklärt, vergeblich:
Schon doch recht deutlich ...Peter0167 schrieb am 22.05.2017:
Es gibt Gleichzeitigkeit, aber sie ist relativ, d.h. sie ist abhängig vom Bezugssystem. Grundsätzlich kann man sagen, wenn ein Beobachter 2 getrennte Ereignisse als gleichzeitig wahrnimmt, dann sind sie für ihn auch gleichzeitig, egal wie ein anderer Beobachter die Ereignisse wahrnimmt.nocheinPoet schrieb am 21.05.2017:In der Physik geht es nun nicht wirklich um das was man so glaubt. ;) Objekte selber sind keine Bezugsysteme, ein Bezugssystem ist abstrakt, nur definiert, kann man nicht real anfassen. In so einem System gibt man dann eben Objekte an. So ein System "endet" auch nicht wirklich wo, Du kannst also ein Bezugssystem definieren und in dem ruht dann eben das Flugzeug, das ist dann eben das Ruhesystem des Flugzeuges. Ebenso kannst Du ein weiteres definieren, für einen Beobachter der wo auf dem Flugplatz steht. Im Ruhesystem des Flugzeuges ist der Flugplatz bewegt und im Ruhesystem des Flugplatzes ist das Flugzeug bewegt.
Ruhen zwei Beobachter zueinander, sind räumlich getrennte Ereignisse für beide gleichzeitig, wenn diese für einen gleichzeitig sind. Sie können sich also darüber einigen, ob diese gleichzeitig sind.
Für zwei zueinander bewegte Beobachter ist das nicht mehr so, hier kommt die Relativität der Gleichzeitigkeit ins Spiel, was für einen Beobachter gleichzeitig ist, ist für einen anderen nicht mehr gleichzeitig und umgekehrt. Kann das gerne genauer und mit Beispiel erklären.
Und es ist auch Quatsch was der Poet schreibt, auch wenn zwei Beobachter im selben Bezugssystem sind, können sie räumlich getrennte Ereignisse unterschiedlich wahrnehmen. Kann man ganz simpel am Beispiel von Lesch erkennen: 1 Zug bewegt sich gleichförmig, 1 Beobachter ist in der Mitte des Zuges, 1 Beobachter ist in der Lok. Beide Beobachter ruhen also zueinander! Dann schlägt ein Blitz in der Lok ein, und einer am Ende des Zuges. Der Beobachter in der Mitte nimmt sie gleichzeitig wahr, der Beobachter in der Lok nicht. Und Beide haben recht.
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:48@intruder
Ich deine Satz mal überarbeitet:
Angenommen jemand würde sich mit c von dem Ereignis entfernen, dann würde für den das Ereignis nie stattfinden, und jemand der entsprechen weit weg von der Ereignis ist, würde es entsprechend später wahrnehmen, für den würden die Ereignisse immer noch gleichzeitig stattfinden
Ich weiß jetzt nicht mehr von wie vielen Ereignissen usw du geredet hast aber ich hoffe ich konnte mich verständlcih machen.
@Peter0167
Ja, das ist so richtig. Aber du siehst warnehmen, ist ein schlechtes Wort. Stattfinden würde hier besser passen:intruder schrieb:Angenommen jemand würde sich mit c von dem Ereignis entfernen, der würde natürlich nie das Ereignis wahrnehmen, und jemand der entsprechen weit weg von der Ereignis ist, würde es entsprechend später wahrnehmen, aber immer noch gleichzeitig.
Ich deine Satz mal überarbeitet:
Angenommen jemand würde sich mit c von dem Ereignis entfernen, dann würde für den das Ereignis nie stattfinden, und jemand der entsprechen weit weg von der Ereignis ist, würde es entsprechend später wahrnehmen, für den würden die Ereignisse immer noch gleichzeitig stattfinden
Ich weiß jetzt nicht mehr von wie vielen Ereignissen usw du geredet hast aber ich hoffe ich konnte mich verständlcih machen.
@Peter0167
Habs nochmal korrigiert.Peter0167 schrieb:Ginge es um die Frage nach der Gleichzeitigkeit beider Ereignisse, dann trifft das zu was du sagst, geht es aber nicht, da nach der Wahrnehmung gefragt wurde.
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:53Für mich ist der Prozess des Wahrnehmens ein grundsätzlich anderer als der des Stattfindens, daher kann man Stattfinden auch nicht mit Wahrnehmen ersetzen und umgekehrt.mojorisin schrieb:Ja, das ist so richtig. Aber du siehst warnehmen, ist ein schlechtes Wort. Stattfinden würde hier besser passen
Wenn es dem Fragesteller (intruder) nun mal um die gleichzeitige Wahrnehmung geht, und nicht ums "Stattfinden", wie hätte er sich denn besser ausdrücken können/sollen?
nocheinPoet

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

anwesend
dabei seit 2006
dabei seit 2006
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:53@Peter0167
Solltest da besser acht geben hier User nicht noch zusätzlich in den Nebel zu führen, reicht doch, wenn da einer drin verloren scheint.
Nein Du irrst, musst mal den Beitrag zu Ende lesen, er schreibt:Peter0167 schrieb:Alles schön und gut, aber es ging in der Frage niemals darum ob die Ereignisse gleichzeitig geschehen, sondern ausschließlich um die Wahrnehmung von Gleichzeitigkeit bei unterschiedlichen Beobachtern im gleichen Ruhesystem! Hier noch mal der unveränderte Originaltext:
Ginge es um die Frage nach der Gleichzeitigkeit beider Ereignisse, dann trifft das zu was du sagst, geht es aber nicht, da nach der Wahrnehmung gefragt wurde.intruder schrieb:Es gibt 2 Ereignisse die jemand als gleichzeitig wahrnimmt. Ich stelle mir hier 2 Bälle vor, die auf den Boden auftreffen. Wenn ich das Ereignis als gleichzeitig wahrnehme, muss jeder andere auch das Ereignis als gleichzeitig wahrnehmen, wenn auch nicht gleichzeitig mit mir.
Da schreibt er es explizit: "... nur der Zeitpunkt ... über das Auftreffen auf dem Boden ...", es geht um die Zeitkoordinate des Ereignisses, nicht um die Zeitkoordinate an dem eine Person dieses Ereignis selber misst.intruder schrieb:Angenommen jemand würde sich mit c von dem Ereignis entfernen, der würde natürlich nie das Ereignis wahrnehmen, und jemand der entsprechen weit weg von der Ereignis ist, würde es entsprechend später wahrnehmen, aber immer noch gleichzeitig. Welche Geschwindigkeit die Bälle haben spielt dafür keine Rolle, da nur der Zeitpunkt entscheidend ist, in dem die Information über das Auftreffen auf dem Boden entsteht.
Solltest da besser acht geben hier User nicht noch zusätzlich in den Nebel zu führen, reicht doch, wenn da einer drin verloren scheint.
Schwierigkeit der Längenkontraktion
05.10.2017 um 13:56Schwierigkeit der Längenkontraktion
05.10.2017 um 13:58@mojorisin
@nocheinPoet
@Peter0167
Ja, die Verwirrung entsteht durch meine "unkorrekte" und eher umgangssprachliche Ausdrucksweise. Danke für die Erklärung. So wie ich mich ausgedrückt habe sind beide Interpretationen möglich. Grundsätzlich wollte ich schon auf die Zeitpunkt des auftreffens und nicht die Wahrnehmung hinaus.
@Peter0167
Hatte dir ja schon recht gegeben und geschrieben, dass ich deine Interpretation bei meiner Überlegung nicht bedacht hatte.
@nocheinPoet
@Peter0167
Ja, die Verwirrung entsteht durch meine "unkorrekte" und eher umgangssprachliche Ausdrucksweise. Danke für die Erklärung. So wie ich mich ausgedrückt habe sind beide Interpretationen möglich. Grundsätzlich wollte ich schon auf die Zeitpunkt des auftreffens und nicht die Wahrnehmung hinaus.
@Peter0167
Hatte dir ja schon recht gegeben und geschrieben, dass ich deine Interpretation bei meiner Überlegung nicht bedacht hatte.
