Schwarze Löcher

Nachtrag zum obigen Bild (die Bearbeitungsfrist war mal wieder zu kurz): bei 2.3·10⁴² kg würde die 1g Grenze genau mit der Photonensphäre von 1.5rs zusammenfallen.

@pukahontas

Schön wäre für die y-Achse eine Angabe in Metern.
Dann kann man sich das besser vorstellen.

pukahontas schrieb:perttivalkonen schrieb:
Dann hat dieses SL eine Masse von X mal A, einen Schwarzschildradius von X mal B, eine Fluchtgeschwindigkeit von v=c, eine Fallbeschleunigung von D geteilt durch X und auch eine mittlere Dichte von E geteilt durch X.

Wir sind ja nicht bei Newton. Bei Schwarzschild ist die benötigte Kraft um stationär zu bleiben wie bereits in einem früheren Beitrag erwähnt nicht GMm/r² sondern GMm/r²/√(1-rs/r). Das geht am Horizont immer gegen unendlich.

So, heute wollt ich mich nochmal dazu umschauen. Und prompt der erste Link, den ich bei meiner Recherche gefunden und angeklickt hab, führte mich zu dieser PDF: https://www.haw-hamburg.de/fileadmin/user_upload/SchulCampus/Downloads/3.SG-Rs.pdf (haw-hamburg steht für Hochschule für angewandte Wissenschaften ebendort).

Und was wird einem da vorgerechnet? Daß die Fallbeschleunigung am EH eines SL von 12 Milliarden Sonnenmassen 129g beträgt.

Also doch nicht so, wie Du behauptet hast.

OK, dann hab ich mir mal die Formeln näher angeschaut. Und Tatsache, sie verwenden die nach dem Newtonschen Gravitationsgesetz. Und geben sogar nen entsprechenden Link zur Wikipedia dazu an. Da kann ich mich ja geehrt fühlen, daß ich mit diesem Fehler nicht allein dastehe...

@pukahontas

pukahontas schrieb:Ich habe mal probegerechnet wann das der Fall wäre (das Wort "knapp" habe ich in dem Fall so interpretiert dass die Höhe über dem Horizont ein Bruchteil des Horizontradius ist). Ab einer Masse von 10⁴³ kg ist man dabei:

Ok dann häte ich zwei Fragen (Oder mehrere :-))

Kann ich g = 9,81 m/s^2 am EH erreichen? Ich denke ja.

Kann ich am EH verweilen wenn ich eine Rakete habe die den Schub leistet um mit g beschleunigen zu können?
Ich denke nein.

Nur versuche ich gerade rauszufinden was der Unterschied wäre zwischen der Erdoberfläche die g = 10 m/s² Erdbeschleunigung aufweist und einem Schwarzen Loch das am EH eine Gravitationsbeschleunigung von 10 m/s² aufweist?

Wobei es gibt auch eine nichtrelativistische Formel für die FLuchtgeschwindigkeit:



Das heißt bei gleichem g steigt mit zunehmendem Radius die Fluchtgeschwindigkeit. Mein Problem hier ist, da muss ich noch drüber brüten, wie der Zusammenhang ist zwischen Fluchtgeschwindigkeit und Gravitationsbeschleunigung.

Wieso kann ich einem SL mit einer so geringen Anziehungskraft nicht entkommen?

perttivalkonen schrieb:Und was wird einem da vorgerechnet? Daß die Fallbeschleunigung am EH eines SL von 12 Milliarden Sonnenmassen 129g beträgt.

Der Fehler liegt bei dir, bei genauer Lektüre dieses Fadens stellt sich nämlich heraus dass

pukahontas schrieb am 26.04.2019:Tatsächlich ist das was du anscheinend meinst aber das d²r/dτ² des Freifallers, wobei r der Koordinatenradius und τ dessen Eigenzeit ist. Die Kraft um stationär zu bleiben enthält den Faktor 1/√(1-rs/r), die ist also am Horizont unendlich.

Mit dem Fehler den unkontrahierten Koordinatenradius und die Eigenzeit mit dem physikalischem Abstand und der absoluten Zeit zu verwechseln stehst du aber dennoch nicht alleine da, das machen viele die Newton mit Einstein verwechseln.

Nachtrag aufgrund der zu kurzen Bearbeitungsfrist:

www.astro.umd.edu/~miller/teaching/astr498/lecture10.pdf (Cole Miller)
What about in strong gravity? First consider radial motion. Then d²r/dτ²=GM/r². This has the same form as the Newtonian expression, but remember that the coordinates mean different things, so you have to be careful.

Wenn man frei fällt ist es natürlich klar dass man nicht unendlich stark beschleunigt (man soll ja ohne etwas Besonderes zu bemerken durch den Horizont fallen), das wäre nur der Fall wenn man versucht stationär zu bleiben (siehe den Unterschied zwischen g und d²r/dτ²).

mojorisin schrieb:Kann ich am EH verweilen wenn ich eine Rakete habe die den Schub leistet um mit g beschleunigen zu können?
Ich denke nein.

Nur versuche ich gerade rauszufinden was der Unterschied wäre zwischen der Erdoberfläche die g = 10 m/s2 Erdbeschleunigung aufweist und einem Schwarzen Loch das am EH eine Gravitationsbeschleunigung von 10 m/s2 aufweist?

Am EH kann man nicht verharren, auf der Eedoberfläche schon. Hast du deine Frage damit nicht selbst beantwortet? Oder was meinst du genau?

@Arrakai

Arrakai schrieb:Am EH kann man nicht verharren, auf der Eedoberfläche schon. Hast du deine Frage damit nicht selbst beantwortet? Oder was meinst du genau?

Mit einer Rakete kann ich 1g Schub erzeugen und mich gegenüber der Erde stationär aufhalten also schweben. Am Ereignishorizont geht das nicht. Wieso?

mojorisin schrieb:Mit einer Rakete kann ich 1g Schub erzeugen und mich gegenüber der Erde stationär aufhalten also schweben. Am Ereignishorizont geht das nicht. Wieso?

@pukahontas schrieb:
Bei Schwarzschild ist die benötigte Kraft um stationär zu bleiben wie bereits in einem früheren Beitrag erwähnt nicht GMm/r² sondern GMm/r²/√(1-rs/r). Das geht am Horizont immer gegen unendlich.

Er ignoriert anscheinend alle meine Beiträge, du wirst es ihm also in eigenen Worten erklären müssen oder es so wie ich es jetzt auch tun werde aufgeben.

pukahontas schrieb:Der Fehler liegt bei dir, bei genauer Lektüre dieses Fadens stellt sich nämlich heraus

Ähm, da haste wohl meinen Beitrag nicht richtig gelesen. Genauer gesagt, den letzten Absatz nicht gelesen:

perttivalkonen schrieb:OK, dann hab ich mir mal die Formeln näher angeschaut. Und Tatsache, sie verwenden die nach dem Newtonschen Gravitationsgesetz. Und geben sogar nen entsprechenden Link zur Wikipedia dazu an. Da kann ich mich ja geehrt fühlen, daß ich mit diesem Fehler nicht allein dastehe...

perttivalkonen schrieb:Ähm, da haste wohl meinen Beitrag nicht richtig gelesen. Genauer gesagt, den letzten Absatz nicht gelesen:

Dieses PDF stammt wohl aus einer Waldorfschule, dort stehen ja gleich auf der ersten Seite solche Sachen wie

https://www.haw-hamburg.de/fileadmin/user_upload/SchulCampus/Downloads/3.SG-Rs.pdf
Zusammenfassung: 1. Mit einer „Superrakete“ kann man den Ereignishorizont einer Schwarzen Galaxie überschreiten.
2. Bei einer Schwarzen Galaxie mit der Masse von 12 Milliarden Sonnenmassen benötigt man dazu eine Beschleunigung von 129 g.

Warum das Unfug ist muss ich hoffentlich niemandem erklären, denn dass ein schwarzes Loch kein schwarzes Loch wäre wenn es nur einen Ferrari bräuchte um von dort wieder herauszufahren ist vermutlich jedem außer den Autoren dieses Witzblatts klar.

pukahontas schrieb:Er ignoriert anscheinend alle meine Beiträge

Wie ich gerade sehe ignorierst du eh nicht alle sondern nur manche, daher versuche ich es nochmal:

mojorisin schrieb:da muss ich noch drüber brüten, wie der Zusammenhang ist zwischen Fluchtgeschwindigkeit und Gravitationsbeschleunigung.

Den Zusammenhang wirst du nicht finden da dir die Fluchtgeschwindigkeit alleine nur einen Faktor, aber nicht das ganze Ergebnis liefert. Bei Newton ist g sowohl die Koordinatenbeschleunigung mit der man frei fällt als auch die spezifische Kraft die man benötigen würde um sich der Beschleunigung zu widersetzen, bei Einstein ist das aber nicht das Gleiche daher musst du dir als Erstes bewusst werden was du unter g verstehst.

@pukahontas

pukahontas schrieb:Den Zusammenhang wirst du nicht finden da dir die Fluchtgeschwindigkeit alleine nur einen Faktor, aber nicht das ganze Ergebnis liefert.

Ich verstehe, es ist die gravitative Zeitdilatation die noch eine Rolle spielt. Ich muss mir das nochmal in RUhe reinziehen aber danke mal für die Antworten.

pukahontas schrieb:Wie ich gerade sehe ignorierst du eh nicht alle sondern nur manche, daher versuche ich es nochmal:

Ich ignoriere keine Beiträge, aber so schnell wie hier momentan geschrieben wird komme ich nicht mit, da ich nebenher was anderes mache :-)

Schönen abend euch ;-)

mojorisin schrieb:Ich verstehe, es ist die gravitative Zeitdilatation die noch eine Rolle spielt.

Am nachvollziehbarsten wird es im Flussmodell, da die meisten bereits aus der SRT wissen dass man beschleunigen kann wie man will ohne trotzdem je die Lichtgeschwindigkeit erreichen zu können ist es dann nur noch ein kleiner Schritt zur Einsicht warum man selbst bei maximaler Beschleunigung nicht schneller herausschwimmen könnte als der Raum hineinfließt.

@pukahontas

pukahontas schrieb:da die meisten bereits aus der SRT wissen dass man beschleunigen kann wie man will

Danke, ja das macht Sinn.

skagerak schrieb:Konstant beschleunigt impliziert doch dass es "immer stärker" beschleunigt mMn. Also konstant immer schneller, sozusagen.

Moin Skagerak...
Konstant beschleunigt meint... zB... je abgelaufene Sekunde, kommen jeweils zB. 9 m dazu...
Nach der ersten Sek hast du eine Geschwindigkeit (v) von 9 m/s, nach der 2ten Sek eine v von 18m/s, nach der 3ten v = 27m/s und so weiter und sofort...

Im Freifall auf den EH kann man das so.. natürlich nicht anwenden, da ist die Beschleunigung nicht konstant, wie im Beispiel drüber.

Ganz einfach weil wir ein asymptotes G-Feld (wie ja schon mehrmals versucht zu erklären) und kein homogens Feld anliegen haben, welches dich je vergehender Sek immer mit dem gleichen Wert beschleunigen würde.
Wikipedia: Asymptote

Man kann´s auch mit ner banalen 2D Graphic eines G-Feldes verdeutlichen:
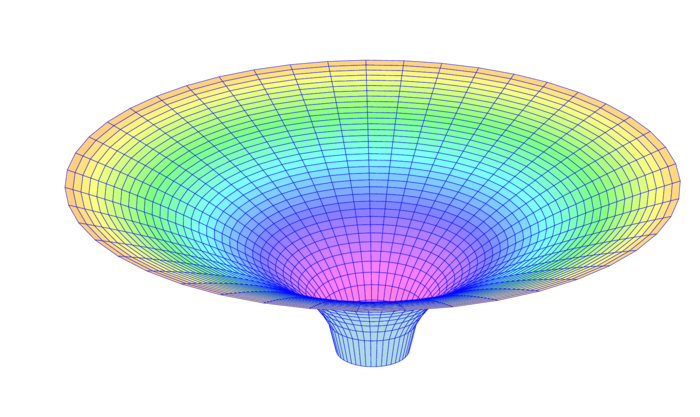Original anzeigen (0,7 MB)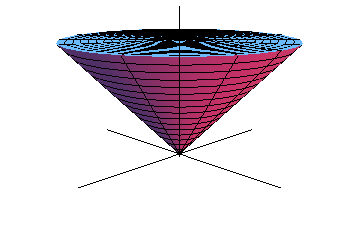
Schwarzes Loch. Am äusseren Rand wirst du schwach, nach innen immer stärker beschleunigt.
Die Krümmung (Gefälle) nimmt also zu, je näher dem gedachten Zentrum und je stärker diese, umso stärker wirst du G-Beschleunigt.. oder eben schneller fällst du. Ein Beispiel für asymptote Beschleunigung wäre zB die Abfolge 9/27/108/540m/s ....

Wäre das Feld homogen "gekrümmt", besser das Gefälle homogen, würde das einfallende Objekt konstant beschleunigt, dann sähe das Feld so aus:

Bis zum Zentrum, immer das gleiche Gefälle... 9/18/27m/s..

Noch ein Beispiel...
(wo anscheinend auch der Fehler drin ist, dass man vor EH eines 2 Billionen M☉ (Sonnenmassen) schweren Lochs, mit nur ~1 g stehen könnte).... ist hier einzusehen:
Lochmasse = 10 M☉
https://www.tempolimit-lichtgeschwindigkeit.de/expeditionsl/expeditionsl.html
In 150 Km Abstand zum EH (Ereignishorizont) wirst du mit 9 Mrd. g gravitationsbeschleunigt...
bei 90 Km sinds 30 Mrd. g
bei 45 Km bereits mit 100 Mrd. g

Hoffe das hilft..
NG ,)

Z. schrieb:Noch ein Beispiel... (wo anscheinend auch der Fehler drin ist, dass man vor EH eines 2 Billionen M☉ (Sonnenmassen) schweren Lochs, mit nur ~1 g stehen könnte).... ist hier einzusehen: tempolimit-lichtgeschwindigkeit.de/expeditionsl/expeditionsl.html

Da ist dieser Fehler nicht drin, die verwenden die richtige Formel. Wenn bei M=2Msol und r=1.005rs ca. 1g herauskommt kommt bei r=rs unendlich raus:

pukahontas schrieb:Wenn bei M=2Msol

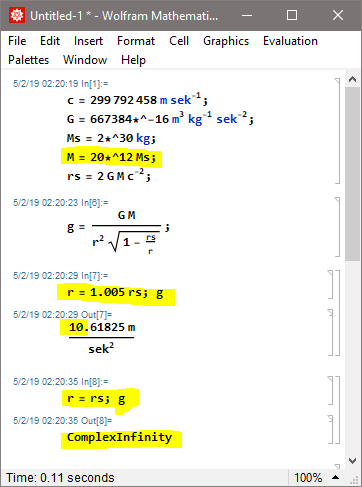
Ich meine natürlich 20e12 Msol = 4e43 kg, so wie es auf



steht. (Bearbeitungszeit mal wieder abgelaufen, aber in der Rechnung im Bild ist es eh richtig)

@pukahontas
Moin...

Nun die Berechung mag stimmen, bei mir kam sowas wie ~ 0.77 g raus.. aber da steht.. man könnte bei r = 1.005rs fachen vor dem EH stehen (verharren) ???... soweit ich das deute.


Ps: Na klar meintest du 20 Billionen M☉... det is scho klar... Meister.