Was ist hinter den Grenzen des Universums?

@Z.

Z. schrieb:ich würde dich sehr bitten mir den Widerspruch zwischen Zeh und dennoch erörterten Paralellwelten auszureden oder zumindest zu bewerten.

Die Aussagen von Zeh beziehen sich auf die klassische Viele-Welten-Interpretation. Und die widerspricht natürlich der von LeviaX1 genannten Interpretation, da es ganz unterschiedliche Ansätze sind.

Aber beides sind eben nur Interpretationen der QM. Darum macht es imho keinen Sinn, mit der Einen gegen die Andere zu argumentieren.

@perttivalkonen
@TangMi

Gut. Dann habe ich wohl tatsächlich mehr hineininterpretiert als ich hätte dürfen. Dann entschuldige ich mich für die angerichtete Verwirrung bezüglich der Vorläufer-Universen. :)

TabbysStar schrieb:Die Thermodynamik kann deduktiv aus den mikroskopischen Gesetzen hergeleitet werden. Sie basiert auf Ihnen. Damit ist dein Einwand irrelevant.

Was soll jetzt irrelevant sein? In welchem abgeschlossenen System gilt die Thermodynamik nicht gnadenlos? Nur Teilsysteme davon, geschlossene, offene eben, nur solche können auch mal ihre Entropie verringern, aber nur, weil ein anderes Teilsystem den Preis dafür bezahlt. Da kannst Du die Thermodynamik sonstwie aus anderen Gesetzen herleiten und meinen, diese Gesetze selbst würden spiegelbildlich, nicht zeitabhängig gelten - das "Gesetz", daß die Thermodynamik zeitlich gerichtet ist, steht dennoch unveränderlich "darüber".

TabbysStar schrieb:Die gesamte moderne Physik basiert darauf, dass es Symmetrien in der Natur gibt.

Tu ich das ab? Nenn ich das Mumpitz? Nö, im Gegenteil, ich verwies selbst auf ein Beispiel dieser Symmetrie. Die ballistische Kurve eines hochgeworfenen Steines ist spiegelsymmetrisch. Nur eben leider - beinahe. Denn sobald da Energieumwandlungen bei stattfinden (Luftwiderstand zum Bleistift), isses aus mit der exakten Spiegelbildlichkeit.

Symmetrien gibt es, keine Frage. So lange, bis ein äußerer Einfluß hinzukommt. Was praktisch immer der Fall ist. Mit anderen Worten: Symmetrien gibt es - theoretisch, auf dem Papier, in der Realität nur näherungsweise.

Mumpitz ist was anderes, nicht die Physik.

TabbysStar schrieb:Und wenn du nicht argumentieren kannst, außer das aus deinem Bauchgefühl heraus zu wissen glaubst, dass das Widerkehrtheorem keinen Realitätsbezug hat, dann erübrigt sich auch jegliche Diskussion.

Wer von uns nahm drei Jahre später die Diskussion wieder auf?

@ilchegu

Ich habe es so verstanden, vor allem auch den weiterführenden Text der Erörterungen zur Quantenmechanik enthält,
das die Quantenmechanik an sich keine realen Parallelwelten zulässt.
In sofern wäre doch eher eine veränderte QM nötig?

NG

Und klassich trifft auch imho nicht zu.

perttivalkonen schrieb: In welchem abgeschlossenen System gilt die Thermodynamik nicht gnadenlos?

Nein, siehe Poincare.

perttivalkonen schrieb:Da kannst Du die Thermodynamik sonstwie aus anderen Gesetzen herleiten und meinen, diese Gesetze selbst würden spiegelbildlich, nicht zeitabhängig gelten - das "Gesetz", daß die Thermodynamik zeitlich gerichtet ist, steht dennoch unveränderlich "darüber".

Und das sagt dir ausschließlich dein Bauchgefühl, Glückwunsch.

perttivalkonen schrieb:Tu ich das ab? Nenn ich das Mumpitz?

Ja, hier:

perttivalkonen schrieb:Das ist genau dasselbe, wie sämtliche Naturgesetze auf dem Papier auch zeitumgekehrt funktionieren. Schön, nur klappt das eben in der Realität dennoch nicht.

Die Energieerhaltung, zum Beispiel, ist eine Folgerung daraus. Man hat noch nie, in keinem Experiment, eine Abweichung davon gefunden.

perttivalkonen schrieb:Wer von uns nahm drei Jahre später die Diskussion wieder auf?

Bestes Beispiel dafür, dass du dich nicht weiter entwickelt hast und das Forum sich im Kreis dreht. Ich hab die Physik hinter mir, du dein Bauchgefühl. Immerhin.

@ilchegu
Das Problem ist doch... Das Tegmark und alle anderen Parallelwelten Vertreter auf die QM fundieren, wie auch Zeh.
Wenn nun aber jeder der Burschen eine andre Auffassung der QM hat... bringt das reichlich Chaos.

Es ging mir dies bzgl. eben genau darum das mir ein Physiker (wenn schon mal da) die Unterschiede gegensätzlicher Auffassungen der QM näher bringt....

Wenn der Diskuss schon soweit ist, das die Grundlagen ...die QM.... einfach so interpretiert werden können wie es einem zur eigenen, letzterer übergestülpten, Theo passt, dann gut Nacht und Willkommen Interpretationschaos und im Bücherwald der Science Fiction. Besser als dieses Forum und deren User ist das dann sicher NICHT!

Ich halte Zeh für einen Meilenstein und seine Interpretationen für äusserst fundiert.
Warum keine Antwort kommen wird ist jedoch mit hoher Wahrscheinlichkeit klar.

Es liegt imho an 2 Dingen, die eine betr. eigener Wissenstand (QM), die andere, Vorsicht die eigene Reputation und Karriere betreff, somit offiziellen Widerspruch zu Spitzentheoretikern, Koryphäen wie Zeh, zu vermeiden.

Von meiner Seit ist das abgehackt.

NG
Ps
Ich hoffe nur das Tabby noch Antwortet.

TabbysStar schrieb:Nein, siehe Poincare.

Ah, verstehe, es gilt auf dem Papier. Ein mathematischer Beweis diktiert die Realität.

TabbysStar schrieb:Und das sagt dir ausschließlich dein Bauchgefühl, Glückwunsch.

Empirie. Experimente, wiederholbare. Die Realität eben. Oder um mit Deinen Worten zu sprechen:

TabbysStar schrieb:Man hat noch nie, in keinem Experiment, eine Abweichung davon gefunden.

Außer in offenen/geschlossenen Systemen, wenn ein "Nachbar" den Entropiezuwachs-Preis dafür zahlte.

perttivalkonen schrieb:
Tu ich das ab? Nenn ich das Mumpitz?


Ja, hier:

perttivalkonen schrieb:
Das ist genau dasselbe, wie sämtliche Naturgesetze auf dem Papier auch zeitumgekehrt funktionieren. Schön, nur klappt das eben in der Realität dennoch nicht.


Die Energieerhaltung, zum Beispiel, ist eine Folgerung daraus. Man hat noch nie, in keinem Experiment, eine Abweichung davon gefunden.

Scherzkeks. Die Energieerhaltung funzt genauso wie der zweite Hauptsatz der Thermodynamik quer durch alle anderen Naturgesetze. Egal, was Du betrachtest, egal, welchen Gesetzen das folgt, daß es so läuft, Energieerhalt und zweiter Hauptsatz kommen immer bei vor und werden immer eingehalten. Das sind mehr Eckdaten als konkrete Gesetze, die die Realität regeln. Hingegen was die Fallbeschleunigung bewirkt und regelt, läuft nicht quer durch alle andere Gesetze und Prozesse und pocht da auf Einhaltung, etwa bei Redoxreaktionen.

Wenn Du in Physik besser bewandert bist als ich, ich nehms einfach mal an, dann weißt Du, daß Du eben nur getrickst hast. Und zwar ziemlich schlecht. Und wenn Du wissen willst, was ich Mumpitz nenne, dann genau sowas. Nicht adäquates Übertragen.

Selbstverständlich läuft der Energieerhalt spiegelbildlich - und er kann eben nicht durch Einflüsse aus seiner Spiegelbildlichkeit gerissen werden. (Naja, lassen wir die Dunkle Energie mal außen vor, da gabs hier mal ne Diskussion mit der Behauptung, daß die DE bei Expansion pro Kubikmeter nicht weniger würde, da kenn ich mich nicht aus.) Sowas würd ich nie Mumpitz nennen.

@Z.

Z. schrieb:Wenn der Diskuss schon soweit ist, das die Grundlagen ...die QM.... einfach so interpretiert werden können wie es einem zur eigenen, letzterer übergestülpten, Theo passt, dann gut Nacht und Willkommen Interpretationschaos und im Bücherwald der Science Fiction. Besser als dieses Forum und deren User ist das dann sicher NICHT!

Ich verstehe Dein Problem hier nicht so ganz. Für die QM existieren seit jeher verschiedene Interpretationen (Kopenhagener Deutung, Viele Welten, etc.). Diese Interpretationen ändern ja nichts an den Ergebnissen der QM, sind experimentell nicht überprüfbar und beziehen sich mehr auf metaphysische Aspekte.

@ilchegu
Sag ich doch.
Kein Deut besser als hier, der Sektor.
NG
.

@Z.

Du siehst da drin viel mehr als da eigentlich ist.

Ganz einfach erklärt. Betrachte eine Newtonsche Welt. Du hast ein Apfel und lässt ihn fallen. Die Gesetzmäßigkeit oder die Mathematik dafür ist dir bekannt. Was siehst du? Fällt der Apfel auf die Erde oder die Erde auf den Apfel? Beide Interpretationen werden durch die gleiche Mathematik beschrieben und beide führen zum selben Ergebnis der Falldauer, Strecke etc. Jetzt hänge dich bitte nicht an Spitzfindigkeiten in diesem Beispiel auf. Es soll nur zeigen. Was ist Realität? Keine Ahnung. Die Mathematik der Quantenmechanik erklärt die verifizierbaren Größen sehr genau. Die Interpretation scheint durch ihren probabilistischen Zusammenhang viele Möglichkeiten zu besitzen. Physiker stören sich in der Regel nicht an der Art der Interpretation und schon garnicht, wenn sie ununterscheidbar sind.

@perttivalkonen

perttivalkonen schrieb:Die Energieerhaltung funzt genauso wie der zweite Hauptsatz der Thermodynamik quer durch alle anderen Naturgesetze.

Nein, das wird auch nicht richtiger, wenn du es häufiger wiederholst. Machen wir noch einmal ein Gedankenexperiment. Das du das alles nicht verstehen willst, habe ich nun kapiert. Vielleicht will das ja jemand anderes nochmal erklärt kriegen und da ich mich vor meiner Arbeit drücke:

Betrachten wir folgende zwei Behälter



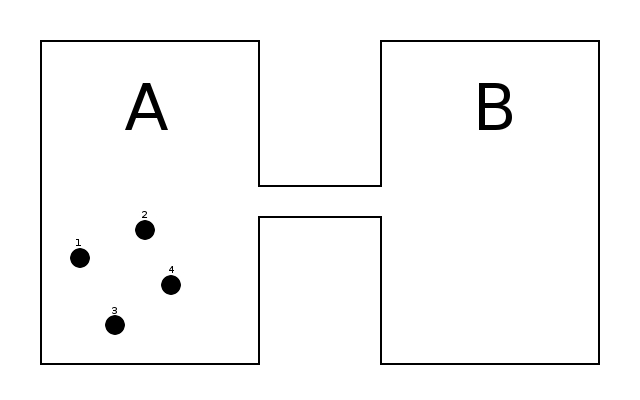
In Behälter A befinden sich vier Teilchen an irgendwelchen Positionen x mit Impulsen p und in Behälter B befindet sich keines der vier Teilchen. A kann nun mit B über die Brücke Wechselwirken. Wir betrachten als unser abgeschlossenes System A vereinigt mit B. Jetzt ist die Entropie ein Maß für die Anzahl der Mikrozustände eines Makrozustands. Welche Makrozustände haben wir?

<table border="1"> <tr> <td>A</td><td>B</td></tr> <tr> <td>4</td> <td>0</td></tr> <tr> <td>3</td> <td>1</td></tr> <tr> <td>2</td> <td>2</td></tr><tr> <td>1</td> <td>3</td></tr><tr> <td>0</td> <td>4</td></tr></table>

Hier steht in den Spalten die Anzahl der Teilchen je Behälter. Wie viele Realisierungsmöglichkeiten gibt es diese Makrozustände durch Mikrozustände zu beschreiben? Beispiel: Das sich in System A 4 Teilchen befinden und in System B 0 entspricht genau einer möglichen Realisierung. Das in System A 3 Teilchen sind und in System B eines entspricht vier möglichen Realisierungen. Wir können jedes der Teilchen {T1,T2,T3,T4} mit einem anderen austauschen und so weiter. Das führt zu

<table border="1"> <tr> <td>A</td><td>B</td><td>Mikro</td></tr> <tr> <td>4</td> <td>0</td><td>1</td></tr> <tr> <td>3</td> <td>1</td><td>4</td></tr> <tr> <td>2</td> <td>2</td><td>6</td></tr><tr> <td>1</td> <td>3</td><td>4</td></tr><tr> <td>0</td> <td>4</td><td>1</td></tr></table>

wo die letzte Spalte der Anzahl an Mikrozuständen entspricht die den dazu gehörigen Makrozustand beschreiben. Man kann jetzt die Entropie explizit berechnen. Für unsere Zwecke reicht aber die Größe in der letzten Spalte. Die Entropie ist folglich maximal, wenn wir die Gleichverteilung haben.

Es gibt damit insgesamt 16 verschiedene Mikrozustände die unser System einnehmen kann und 6 von denen repräsentieren den Zustand maximaler (Wahrscheinlichkeit 3/8) und 2 den Zustand minimaler (Wahrscheinlichkeit 1/8) Entropie.

Was pertti nun sagt ist, dass der Zustand minimaler Entropie in unserem Gesamtsystem nicht wieder erreicht werden kann. Macht das Sinn? Was verbietet den Teilchen wieder zurück in Behälter A zu gehen, gleichwohl das sehr viel unwahrscheinlicher ist, als im Zustand maximaler Entropie zu verharren. Ich denke es ist jedem klar (auch pertti) das, wenn man lange genug wartet, sich alle Teilchen auch wieder in System A zusammenfinden können und das sich das System lediglich im Mittel im Zustand maximaler Entropie befindet. So ein Effekt kann auch in der Realität beobachtet werden

Poincaré recurrence theorem

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

oder im Experiment (obwohl es abgesehen vom Universum kein echtes abgeschlossenes System gibt) und das ist auch schon alles, was das Poincaresche Widerkehrtheorem mathematisch sauber formuliert. Je geringer die Teilchenanzahl N desto größer wird der Effekt.

Nebenbemerkung dazu: Betrachten wir ein Mol Gas (6*10^23 Teilchen). Nix besonderes in der Welt da draußen und stecken das in unsere Welt A vereinigt B. Der Zustand minimaler Entropie wird noch immer durch nur zwei Mikrozustände realisiert, derjenige mit maximaler Entropie durch 18*10^46 Mikrozustände. Man kann sich unschwer ausmalen das die Wahrscheinlichkeit, einmal im Zustand maximaler Entropie angekommen wieder zurück zu dem Ausgangszustand zu gelangen sehr gering ist und im Mittel große Zeiten bedarf. Übertragen auf das Universum...

The LONGEST time - Numberphile

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Nerok schrieb:Also ist im Endeffekt überhaupt nichts gewonnen und es ist vollkommen überflüssig darüber nachzudenken.

...das mag aus Deiner Sicht überflüssig sein und aus Perttis Sicht ein sehr dürftiger Beweis - und aus meiner Sicht ist das gar kein Beweis.

Darum geht es mir aber nicht wenn ich solche Sätze formuliere - sondern darum auf zu zeigen das da etwas war was eine ungeheure Macht hatte.
Andere nennen das eine Fluktuation im Nichts. Komischer Weise finden sich hier alle damit ab - bzw. hätte sich nie jemand gemeldet wenn ich gesagt hätte "Das Universum ist aus einer Fluktuation im Nichts entstanden".
Diese Bezeichnung für das woraus alles entstanden ist - ist mir zu dürftig. Ich nenne es deshalb das Potential von "Allem was ist".
Und in diesem Potential steckt auch die Antwort auf alle Fragen, bzw. warum das Universum entstanden ist und warum nicht Nichts ist.

@TabbysStar
Moin...

Ich werde dein "Spizfindig" einfach mal positiv bewerten.
Das man die Aussagen Zehs im verlinkten Paper nicht mit Äpfeln erklären kann dürfte klar sein.
Der Kontext war angefragt. Die Kritik im gesamten Paper ist unübersehbar und geht in etliche Bereiche.
Von welch grossen Gegensätzen das spricht, spricht für sich selbst.
NG

TabbysStar schrieb:Nein, das wird auch nicht richtiger, wenn du es häufiger wiederholst.

Das kann ich Dir genauso sagen. Schon damals vor drei Jahren hab ich Dich drauf aufmerksam gemacht, daß es sich dabei um ne energetische Geschichte handelt. Vier Kugeln können selbstverständlich in jeden dieser Zustände gebracht werden. Können sie sich aber auch in jeden dieser Zustände selbst bringen?

Damals hatten wir ein paar mehr Kugeln, und wir hatten unterschiedlich warme Kugeln, Moleküle eines Gases. Hier wird es dann sinnhafter. Wenn Du in Behälter A ein warmes Gasgemisch hast und in B ein kaltes, dann wird sich dieses Gas über die Brücke mischen, aber es wird sich nie wieder sauber trennen.

Wir können aber auch gerne bei hüpfenden Kugeln bleiben. Da reicht dann sogar ein Behälter. Nimm Behältnis A, schließ die Brücke. Dann leg ein Gitternetz über den Behälter, sodaß sich sechs Reihen und vier Spalten mit 24 Quadraten ergeben. Öffne oben den Deckel des Gefäßes und wirf 24 Flummies rein, schließe schnell wieder den Deckel. Die Flummies hüpfen in dem Gefäß hin und her. Theoretisch könnte bei jedem Hinschauen pro Gitterquadrat ein Flummie anzutreffen sein, wahrscheinlich aber wären pro Schnappschuß mehrere Quadrate mehrfach besetzt und mehrere Quadrate leer. Betrachten wir die sechs übereinanderliegenden Reihen zu je vier Quadrtaten, ist die Wahrscheinlichkeit, daß keine der Reihen unbesetzt ist.

Warte ne Weile, gerne ne Woche. Wie verteilen sich die Flummies? Hüpfen sie noch immer rum. Ich für meinen Teil muß nicht mal hinschauen, ich weiß auch so, daß Fünf der Reihen flummiefrei sind und nur die sechste, die unterste, Flummies beherbergt. Für Dich mag ja die reine arithmetische Verteilung das Entropiemaximum sein, für mich ist das energetische Entropiemaximum erreicht, wenn alle Flummies sich am Boden konzentrieren und ihre Bewegungsenergie in Wärme umgesetzt haben.

Und jetzt schau da gern ein ganzes Jahr auf den Kasten, oder zehn Trilliarden Jahre, oder ein Googolplexplexplex an Jahren. Wird die arithmetische Wahrscheinlichkeit der Flummieverteilung auf alle sechs Reihen jemals wieder eingenommen? Nicht ohne Zufuhr von Energie von Außen!

TabbysStar schrieb:Was pertti nun sagt ist, dass der Zustand minimaler Entropie in unserem Gesamtsystem nicht wieder erreicht werden kann. Macht das Sinn? Was verbietet den Teilchen

Klar kannst Du Deinem Aufbau Energie zuführen, z.B. durch Schütteln des Aufbaus. Dann verändern die Kugeln wieder ihren Ort. Und so kannst Du jede beliebige Konstellation nach ihrer arithmetischen Wahrscheinlichkeit erzielen. Hauptsache, Du führst Energie zu. Dann könntest Du sogar ein unterschiedlich warmes Gasgemisch sauber auf A und B entmischen. Mit ner strombetriebenen temperaturabhängigen Durchlaßsperre etwa. Oder Du nimmst gleich nur vier Gasmoleküle, die sowieso kaum miteinander kollidieren und sich also tatsächlich rein arithmetisch verteilen können.

Nein, nichts verbietet den Teilchen diese Verteilung., jede beliebige Verteilungskonstellation einzunehmen.

TabbysStar schrieb:Ich denke es ist jedem klar (auch pertti) das, wenn man lange genug wartet, sich alle Teilchen auch wieder in System A zusammenfinden können und das sich das System lediglich im Mittel im Zustand maximaler Entropie befindet. So ein Effekt kann auch in der Realität beobachtet werden

Wahrscheinlich kannst Du nun selbst erraten, wo ich den Zustand größter Entropie der pendelnden Kugeln in dem Vid beobachte. Und wo den Zustand der geringsten Entropie. Letzterer wurde übrigens nach dem Start der Pendelaktion nie mehr erreicht.

TabbysStar schrieb:Nebenbemerkung dazu: Betrachten wir ein Mol Gas (6*10^23 Teilchen). Nix besonderes in der Welt da draußen und stecken das in unsere Welt A vereinigt B. Der Zustand minimaler Entropie wird noch immer durch nur zwei Mikrozustände realisiert, derjenige mit maximaler Entropie durch 18*10^46 Mikrozustände. Man kann sich unschwer ausmalen das die Wahrscheinlichkeit, einmal im Zustand maximaler Entropie angekommen wieder zurück zu dem Ausgangszustand zu gelangen sehr gering ist und im Mittel große Zeiten bedarf. Übertragen auf das Universum...

Na machen wir es einfacher. Nimm vier hüpfende Flummies und teil den Behälter nur in der Mitte in oberen und unteren Bereich. Dann hast Du Deine sechzehn Mikrozustände. Nun mußt Du nicht so viele Tests machen, um der erdrückenden Megawahrscheinlichkeit des entropischen Maximums mit Deiner Testreihe Herr zu werden. Nach spätestens hundert Einzeltests sollte so gut wie jede Verteilung bei rausgekommen sein, nicht wahr? Und? Laß mich raten. Selbst Du weißt, daß stets nur ein Ergebnis sich einstellen wird: unten vier, oben null.

@perttivalkonen

Tja, gegen soviel Ignoranz ist kein Kraut gewachsen. Ich spreche hier von einem abgeschlossenem System.

Wikipedia: Abgeschlossenes System

Der Poincaresche Wiederkehrsatz funktioniert logischerweise nur in abgeschlossenen Systemen. Es gibt nur A und B, sonst nichts. Keine Entropie die irgendwo größer wird durch die Minimierung in meinem vereinigtem Gesamtsystem. Was du konstruierst (dafür musst du auch keine 100 verschiedene Aufbauten besprechen, einer reicht) hat nichts mit dem Universum zu tun (deine Flummies geben Wärme an die Umgebung ab, dadurch kannst du das nur näherungsweise für kleine Zeiten t als abgeschlossenes System betrachten, d.h. solange der Wärmeaustausch hinreichend klein ist) und darum ging es ja. Das Universum tauscht keine Energie aus (ein perfektes abgeschlossenes System im thermodynamischen Sinn), zumindest beobachten wir das nicht und es ist legitim davon auszugehen das das auch stimmt. Mein Beispiel entspricht dem Universum. Gravitation ist am Ende auch nichts weiter als die zufällige Verteilung einzelner Massenpunkte und wenn mein Minimalbeispiel funktioniert, funktioniert das auch mit 8, 100, 10^23 oder 10^10^23 Teilchen. Das Wiederkehrtheorem und die Vereinbarkeit mit der statistischen Mechanik haben alle Physiker in ihrem Studium durchgearbeitet. Andere Physiker haben eine Wiederkehrzeit für das Universum berechnet (s. Youtube Link). Doch du weißt es besser.

Ganz ehrlich, dass ist hier nicht das erste mal das Du die Physik und ihre Begriffe nach Herzenslust und Bauchgefühl verwendest. So funktioniert das vielleicht auf Allmy wo dich in der Regel keiner hinterfragt und wo du mit deinem zugegeben erschreckend großem allgemein Wissen glänzen kannst, aber zum Glück nicht in der nicht Tastatur Welt. Es ist fein, wenn du etwas nicht nachvollziehen kannst, aber dein überhebliches daran Klammern immer recht haben zu wollen ist leider traurig.

Letzterer wurde übrigens nach dem Start der Pendelaktion nie mehr erreicht.

Ja, man kann Erbsen zählen. Siehe oben abgeschlossenes System. Es ging auch nur darum, dass hier für eine geringe Anzahl an Teilchen in einer ziemlichen kurzen Zeitspanne unglaublich viele unterschiedliche Zustände angenommen wurden.

PS: Bevor du dir die Mühe machst. Argumente ala, das Universum ist offen, wegen Expansion tralala. Wayn. Es bleibt auch dann noch ein abgeschlossenes System im thermodynamischen Sinn.

EDIT: Nicht das es wichtig ist, aber hab ich übersprungen.

perttivalkonen schrieb:Wenn Du in Behälter A ein warmes Gasgemisch hast und in B ein kaltes, dann wird sich dieses Gas über die Brücke mischen, aber es wird sich nie wieder sauber trennen.

Und wie das der Fall sein wird. Das kannst du rechnerisch zeigen und intuitiv auch ganz leicht verstehen. Fang mit zwei Teilchen an, möglich oder nicht? Und geh dann weiter. Abgesehen von der Wiederkehrzeit spielt es keine Rolle wie viele Teilchen du betrachtest.

@Z.

Z. schrieb:Sag ich doch.
Kein Deut besser als hier, der Sektor.

Doch, da gibt es einen großen Unterschied: Diese Interpretationen stammen vom Physikern, welche die QM bestens beherrschen :)

Dahinter is nichts, jedenfalls nichts das wir wahrnehmen können.

Wir kennen ja noch nich einmal die Grenze unseres Universums. Denn wir schauen nun mal nich nur durch den Raum sondern vor allem durch die Zeit. Eine erkennbare Grenze wäre dann immer eine zeitlich Grenze und niemals eine räumliche.

Wir müssten zunächst einmal die Struktur unseres Universums erkennen um auf dieser Basis Grenzen bestimmen zu können.

Aus meiner Sicht deutet einzig und allein die Dunkle Energie darauf hin dass unser Universum auch nur eine Struktur in einer höherdimensionalen Hierarchie ist. Ähnlich wie die Kugeloberfläche zweidimensional in einem dreidimensionalen Raum existiert.

Würden wir als zweidimensionale Wesen auf einer Kugeloberfläche leben, könnten wir den uns umgebenden dreidimensionalen Raum auch nicht direkt wahrnehmen. Und die Kugeloberfläche wäre für uns unendlich groß, solange niemand sie einmal umrundet hätte.

Gruß greenkeeper

greenkeeper schrieb:Eine erkennbare Grenze wäre dann immer eine zeitlich Grenze und niemals eine räumliche.

Die für uns erkennbare Grösse entspricht dann wohl die des beobachtbaren Universum und nicht der tatsächlichen Grösse des Universums z.Z.

"Aus meiner Sicht deutet einzig und allein die Dunkle Energie darauf hin dass unser Universum auch nur eine Struktur in einer höherdimensionalen Hierarchie ist."

"Über die genaue Natur der Dunklen Energie kann derzeit nur spekuliert werden. Die einfachste Lösung ist, einen geeigneten Wert einer kosmologischen Konstanten zu postulieren und als gegebene und grundlegende Eigenschaft des Universums hinzunehmen."

fritzchen1 schrieb:Über die genaue Natur der Dunklen Energie kann derzeit nur spekuliert werden. Die einfachste Lösung ist, einen geeigneten Wert einer kosmologischen Konstanten zu postulieren und als gegebene und grundlegende Eigenschaft des Universums hinzunehmen."

Trotzdem muss auch die Dunkle Energie eine Ursache haben. Und wenn man diese mit den in unserem Universum geltenden Naturgesetzen nicht erklären kann (siehe Energieerhaltungssatz), dann liegt es nahe dass außerhalb unseres Universums auch noch etwas existieren muss. Und solange wir die Dunkle Energie nich erklären können, können wir uns auch keine Vorstellung machen wie es wohl hinter den Grenzen unseres Universums aussieht.

Wir nehmen an das Universum wäre nach außen hin unendlich, wie siehts denn im Inneren aus? Ich meine rein mathematisch ist es auch in dieser Richtung unendlich, obwohl das ja unseren alltäglichen Erfahrungen vollkommen widerspricht. Wir haben einen abgeschlossenen Raum vor uns, wissen aber dass wir das Volumen darin beliebig in immer kleiner Einheiten aufteilen können ohne jemals eine Volumeneinheit mit der Größe Null zu erreichen. Null ist sowieso nur eine theoretische Zahl, die uns hilft mathematisch mit der Umwelt zurecht zu kommen. Praktisch existiert diese Zahl im Universum eigentlich gar nich.

Gruß greenkeeper

greenkeeper schrieb:Trotzdem muss auch die Dunkle Energie eine Ursache haben. Und wenn man diese mit den in unserem Universum geltenden Naturgesetzen nicht erklären kann (siehe Energieerhaltungssatz),

Siehe auch die Quantenphysik. Demnach kann Energie so quasie aus dem nichts entstehen. :)