In diesem Beitrag soll es um das Thema
Umlaufbahnen (z.B. von Himmelskörpern oder Satelliten) gehen. Der User
@eich-hörnchen hat dazu sehr eigene Ansichten, die er kürzlich im Schwarze-Löcher-Thread geäussert hat, was auf deutliche Kritik von einigen anderen Usern, u.a.
von mir stiess. Da es sich bei Umlaufbahnen im Allgemeinen um ein Physik-Grundlagen-Thema handelt, das in einer ernsthaften Diskussion über Schwarze Löcher nichts verloren hat, möchte ich die Diskussion darüber nach hier verlagern.
Der User
@eich-hörnchen vertritt die Ansicht, dass "jede kleinste Abbremsung" von einer stabilen Umlaufbahn dazu führt, dass das umlaufende Objekt in Richtung des Zentralobjekts abstürzt. Um das zu verhindern, müsse jede dauerhafte Umlaufbahn ein gewisses Abdriften des umlaufenden Objekts vom Zentralobjekt weg aufweisen.
So ganz sicher scheint er sich seiner Sache aber doch nicht zu sein, da er zu dieser Frage -- wobei möglicherweise eine vorübergehende Beurlaubung hier eine Rolle gespielt haben mag -- einen
Thread in einem anderen Forum eröffnet hat. U.a. schimpft er dort auf seine Kritiker hier ("User 001" bin ich, "User 002" ist
@perttivalkonen):
Beispiele von usern, die anderer °Meinung sind, die Unsinn verbreiten, was jedoch befürwortet wird:
User 001:Unsinn. Himmelskörper driften nur dann von ihrer Umlaufbahn ab, wenn es einen konkreten physikalischen Einfluss gibt, der dieses Abdriften bewirkt, nicht weil sie es irgendwie "müssen".
Unsinn. Eine nicht wiederkehrende Abbremsung führt -- von Extremfällen abgesehen -- zu einer anderen, niedrigeren Umlaufbahn, die genauso stabil ist wie die vorhergehende. Nur permanente oder periodisch wiederkehrende Abbremsungen führen zu einem Absturz (z.B. durch Luftwiderstand bei Satelitten).
Diese beiden Punkte zeigen, dass Du noch nicht mal die elementarsten Grundlagen der Himmelsmechanik verstanden hast. Das wäre an sich nicht schlimm, wenn Du nicht gleichzeitig versuchen würdest, andere über Astronomie zu belehren.
user 002:Entsprechend stürzt auch kein Himmelskörper zwangsläufig in sein Zentralgestirn, wenn seine Geschwindigkeit für einen stabilen Orbit ausgebremst wird. Durch den freien Fall in Richtung Zentralgestirn erhöht der Körper seine Geschwindigkeit, bis sie ausreichend hoch für die gerade erreichte Distanz ist, um hier wieder einen stabilen Orbit einzunehmen.
Für meine Begriffe wird von diesen beiden usern totaler Unsinn verbreitet, was aber ganz normal zu sein scheint. Die Rubrik nennt sich übrigens: WISSENSCHAFT, müsste aber Unsinn heißen.
(bumbumpeng aka eich-hörnchen am 05.12.2020)
Die Frage des allgemeinen Verlaufs von Umlaufbahnen ist -- zumindest solange man unterhalb der Grössenordnung von Galaxien bleibt -- keine Frage von
Meinungen. Diese Frage ist seit über 300 Jahren, nämlich seit der Veröffentlichung von Newton's
Principia Mathematica 1687 grundsätzlich geklärt. Es gibt zwar einige extrem geringe Abweichungen, die die Anwendung der allgemeinen Relativitätstheorie erfordern, aber die grösste Abweichung dieser Art im Sonnensystem, die
Periheldrehung des Merkur, beträgt nur 43,11
Bogensekunden (das ist nicht viel mehr als
ein Hundertstel eines Grads)
pro Jahrhundert. Alles andere lässt sich mit klassischer Physik, insbesondere den Newton'schen Gesetzen erklären. Ein Abdriften von einer Umlaufbahn findet nur genau dann statt, wenn es einen
konkreten physikalischen Einfluss (z.B. Gezeitenkräfte) gibt, der dieses Abdriften bewirkt.
Betrachten wir zunächst den einfachsten Fall einer kreisförmigen Umlaufbahn. Sofern die Masse des Zentralobjekts gegenüber dem umlaufenden Objekt als quasi unendlich gross betrachtet werden kann (was z.B. bei Satelliten in der Erdumlaufbahn der Fall ist), und keine relevanten zusätzlichen Kräfte (z.B. Gezeitenkräfte oder Luftreibung) wirken, kann man eine kreisförmige Umlaufbahn durch Gleichsetzen von gravitativer Anziehung und Zentrifugalkraft berechnen. An jedem Bahnpunkt des umlaufenden Objekts wirkt die gravitative Anziehung auf den Schwerpunkt des Zentralobjekts hin, und die Zentrifugalkraft davon weg. Sofern sich beide Kräfte genau gegeneinander aufheben, bleibt der Abstand des umlaufenden Objekts vom Schwerpunkt des Zentralobjekts gleich, was einer Kreisbahn entspricht.
Die gravitative Anziehung berechnet sich gemäss (G = Gravitationskonstante ≈ 6.6743e-11 m^3/(kg*s^2), M = Masse des Zentralobjekts, m = Masse des umlaufenden Objekts, r = Abstand der Schwerpunkte) :
F_g=G*\frac{M*m}{r^2}
Die Zentrifugalkraft (dazu hatte ich vor Längerem in einem anderen Thread mal eine
Herleitung gepostet) berechnet sich gemäss (m = Masse des umlaufenden Objekts, v = Bahngeschwindigkeit des umlaufenden Objekts, r = Abstand der Schwerpunkte):
F_z=\frac{m*v^2}{r}
Gleichsetzen ergibt:
F_g=F_z \quad\longrightarrow\quad G*\frac{M*m}{r^2}=\frac{m*v^2}{r}
Diese Gleichung kann man nun sowohl nach v als auch nach r auflösen:
\begin{aligned}
v&=\sqrt{\frac{G*M}{r}} \\
r&=\frac{G*M}{v^2}
\end{aligned}
Mit diesen beiden Formeln kann man für einen gegebenen Bahnradius die Bahngeschwindigkeit, oder für eine gegebene Bahngeschwindigkeit den Bahnradius berechnen, bei der/dem sich jeweils eine stabile Kreisbahn ergibt. Bemerkenswerterweise kommt die Masse des umlaufenden Objekts in den beiden Formeln gar nicht mehr vor. Solange die Masse des umlaufenden Objekts gegenüber der Masse des Zentralobjekts vernachlässigbar ist, spielt es für die Umlaufbahn tatsächlich keine Rolle, ob das umlaufende Objekt eine Masse von einem Gramm oder 1000 Tonnen hat. Das liegt daran, dass sich die Masse des umlaufenden Objekts auf die gravitative Anziehungskraft genau entgegengesetzt gleich wie auf die Zentrifugalkraft auswirkt.
Als praktisches Beispiel sei die (idealisierte) Berechnung der Bahn für einen geostationären Satelliten betrachtet. Ein geostationärer Satellit umläuft die Erde in einem
siderischen Tag (ca. 86.164 s), genau entsprechend der Rotationsdauer der Erde um sich selbst.
Die Umlaufstrecke des Satelliten hängt vom Bahnradius ab:
s=2*\pi*r
Die Bahngeschwindigkeit ergibt sich aus der Umlaufstrecke und der Umlaufzeit:
v=\frac{s}{T}=\frac{2*\pi*r}{T}
Dieser Ausdruck lässt sich nun für v in die obige Formel für den Bahnradius einsetzen:
r=\frac{G*M}{v^2}=\frac{G*M}{\left(\dfrac{2*\pi*r}{T}\right)^2}
Auflösen nach r und Einsetzen der numerischen Werte ergibt:
r=\sqrt[3]{\frac{G*M*T^2}{4*\pi^2}}=\mathrm{\sqrt[3]{\frac{6{,}6743\times 10^{-11}\,m^3/(kg*s^2)*5{,}9724\times 10^{24}\,kg*(86164\,s)^2}{4*\pi^2}}≈42.164.685\,m}
Abzüglich des Erdradius am Äquator (ca. 6.378 km) entspricht das einem Orbit von ca. 35.787 km Höhe, was weitgehend dem tatsächlichen
Orbit geostationärer Satelliten (üblicherweise als 35.786 km angegeben) entspricht.
Für die Bahngeschwindigkeit ergibt sich:
v=\sqrt{\frac{G*M}{r}}=\mathrm{\sqrt{\frac{6{,}6743\times 10^{-11}\,m^3/(kg*s^2)*5{,}9724\times 10^{24}\,kg}{42.164.685\,m}}≈3075\,m/s}
Was geschieht nun, wenn man das umlaufende Objekt aus einer solchen Kreisbahn heraus beschleunigt oder abbremst? Normalerweise, sofern die resultierende Geschwindigkeit bestimmte Grenzen nicht unter- bzw. überschreitet, entsteht eine Ellipsenbahn,
die genauso stabil ist, wie die vorhergehende Kreisbahn. Das lässt sich auch berechnen, ist allerdings deutlich komplizierter als bei einer Kreisbahn. Das Problem bei solchen Berechnungen ist die fehlende Anschaulichlichkeit für diejenigen, die mit der zugrundliegenden Mathematik nicht vertraut sind. Deshalb erschien es mir sinnvoller, das Ganze anhand einer Simulation zu erläutern.
Es gibt mit dem
Python-basierten
VPython ein Software-Framework, das es erlaubt, mit relativ wenig Aufwand recht absehnliche 3D-Animationen zu erstellen. VPython wurde ursprünglich an der Carnegie Mellon Universität entwickelt, ist Open-Source-Software und für alle gängigen Plattformen frei verfügbar. Ein paar Infos zur Installation und zu speziellen Aspekten finden sich
hier (Archiv-Version vom 13.08.2020). Mit
GlowScript gibt es eine VPython-Variante, bei der die erzeugten Programme im Webbrowser ausführbar sind. Inzwischen wird nur noch diese Variante weiterentwickelt. Eine Sammlung interessanter Beispiele gibt's
hier, besonders gut gefällt mir die folgende
Kreisel-Simulation. Bemerkenswert finde ich, wie wenig Sourcecode viele Beispiele erfordern. Einen wesentlichen Nachteil von VPython möchte ich allerdings nicht verschweigen: Die Programme sind ziemlich langsam. Je nach Anwendungsfall kann das mehr oder weniger problematisch sein.
Zur Simulation von Umlaufbahnen habe ich mit GlowScript die folgende 3D-Animation erstellt. Es ging mir dabei nicht nur um das physikalische Thema selbst, sondern auch darum, VPython/GlowScript etwas bekannter zu machen, und die Grundprinzpien von Bewegungssimulationen zu erläutern. Zunächst das vollständige Programm in der Übersicht:
from vpython import *
#GlowScript 3.0 VPython
# Project: Satellite Simulation
# Version: 0.0
# Date: 2020-12-07
# Developer: Uatu
# Licence: Public Domain
scene.width = 1200
scene.height = 900
scene.forward = vector(0,-0.05,-1)
G = 6.6743e-11 # [m^3/(kg*s^2)] Gravitational constant
Siderial_Day = 86164 # [s]
Initial_Orbit = 35793685 # [m]
Initial_Speed = 3075 # [m/s]
Running = True
Earth = sphere(radius=6371e3, color=vector(0.0,0.5,1.0),
make_trail=True, trail_type='points', interval=5, retain=1000)
Earth.mass = 5.9724e24 # [kg]
Earth.pos = vector(0, 0, 0)
Earth.speed = vector(0, 0, 0)
scene.visible = False
Earth.texture = textures.earth
for i in arange(30):
rate(10)
if Earth.ready: break
if Earth.ready:
Earth.color=vector(1,1,1)
else:
Earth.texture = None
scene.visible = True
Satellite = sphere(radius=1000e3, color=color.gray(0.6),
make_trail=True, trail_type='points', interval=5, retain=1000)
Satellite.mass = 1000 # [kg]
Satellite.pos = vector(0, 0, Earth.pos.x+Earth.radius+Initial_Orbit)
Satellite.speed = vector(Initial_Speed, 0, 0)
def Button_Pause(b):
global Running
Running = not Running
if Running:
b.text = ' Pause '
else:
b.text = 'Continue'
button(text=' Pause ', bind=Button_Pause)
def Button_Accelerate(b):
Satellite.speed = Satellite.speed * 1.05
button(text='Accelerate', bind=Button_Accelerate)
def Button_Decelerate(b):
Satellite.speed = Satellite.speed * 0.95
button(text='Decelerate', bind=Button_Decelerate)
Label_Steps = label(pixel_pos=True, pos=vector(0, 110, 0), align='left', opacity=1,
color=color.green, box=False)
Label_Time = label(pixel_pos=True, pos=vector(0, 80, 0), align='left', opacity=1,
color=color.green, box=False)
Label_Satellite_Orbit = label(pixel_pos=True, pos=vector(0, 50, 0), align='left', opacity=1,
color=color.green, box=False)
Label_Satellite_Speed = label(pixel_pos=True, pos=vector(0, 20, 0), align='left', opacity=1,
color=color.green, box=False)
step = 0
dt = 100
scene.autoscale = False
scene.range = scene.range * 2
while True:
rate(100)
if not Running: continue
r = Satellite.pos - Earth.pos
F = G * Earth.mass * Satellite.mass * norm(r) / mag(r)**2
Earth.speed = Earth.speed + (F / Earth.mass) * dt
Satellite.speed = Satellite.speed - (F / Satellite.mass) * dt
Earth.pos = Earth.pos + Earth.speed * dt
Satellite.pos = Satellite.pos + Satellite.speed * dt
if (Earth.texture != None):
Earth.rotate(axis=vector(0,1,0), (dt / Siderial_Day) * 2 * pi)
Label_Steps.text='Steps: ' + (step + 1)
Label_Time.text='Time: '+ round((step + 1) * dt) + ' s'
Label_Satellite_Orbit.text='Orbit: ' + round(mag(r) - Earth.radius) + ' m'
Label_Satellite_Speed.text='Speed: ' + round(mag(Satellite.speed)) + ' m/s'
step = step + 1Das ist die herunterladbare Sourcecode-Datei:
Dateianhang: Satellite_Simulation.py (2 KB)Dieses Programm wird von der GlowScript-Entwicklungsumgebung (im Webbrowser) in HTML/JavaScript umgewandelt. Die resultierende Animation sieht nach ca. einem Umlauf so aus:
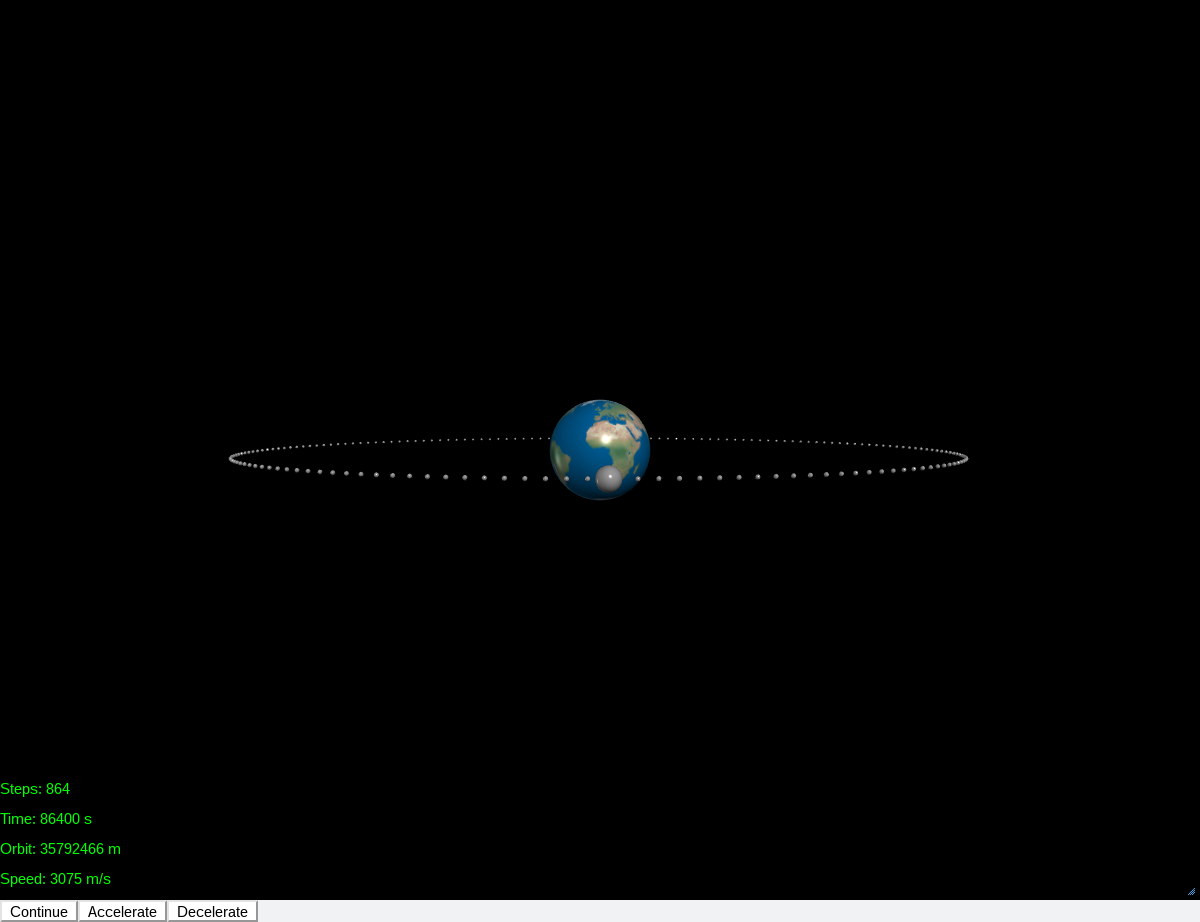
Das ist die HTML/JavaScript-Datei mit der Animation (herunterladen, lokal speichern, und dann im Webbrowser öffnen):
Dateianhang: Satellite_Simulation.html (6 KB)Die GlowScript-Bibliotheken werden dabei von einem von GlowScript bereitgestellten Server geladen, die Animation ist also in dieser Form nicht offline nutzbar (das geht aber auf anderem Wege, dazu komme ich noch).
Die Animation sollte sich idealerweise mit dem Scrollrad zoomen und mit der rechten Maustaste räumlich drehen lassen. Leider funktioniert das aktuell je nach Webbrowser u.U. nur eingeschränkt.
Nun zu den einzelnen Abschnitten des Programms. Der erste Abschnitt enthält einige Standard-Deklarationen. Eine Raute (#) bewirkt, dass die entsprechende Zeile ab dieser Stelle als Kommentar interpretiert wird.
from vpython import *
#GlowScript 3.0 VPython
# Project: Satellite Simulation
# Version: 0.0
# Date: 2020-12-07
# Developer: Uatu
# Licence: Public DomainDer folgende Abschnitt legt die Grösse der "Leinwand" fest, auf der die Animation dargestellt wird, und aus welchem Winkel diese betrachtet wird. Das Koordinatensystem ist folgendermassen ausgerichtet: Die x-Achse verläuft von links nach rechts, die y-Achse von unten nach oben, und die z-Achse vom Hintergrund zum Betrachter hin.
scene.width = 1200
scene.height = 900
scene.forward = vector(0,-0.05,-1)Der folgende Abschnitt legt eine Reihe von globalen Konstanten bzw. Variablen fest, u.a. den anfänglichen Orbit und die anfängliche Bahngeschwindigkeit für den Satelliten. Da die Erde in der Animation aus Vereinfachungsgründen eine ideale Kugel mit einem einheitlichen Radius ist, unterscheidet sich der Wert für den anfänglichen Orbit geringfügig von dem in der obigen Rechnung.
G = 6.6743e-11 # [m^3/(kg*s^2)] Gravitational constant
Siderial_Day = 86164 # [s]
Initial_Orbit = 35793685 # [m]
Initial_Speed = 3075 # [m/s]
Running = TrueDer folgende Abschnitt legt die Daten für die Erde fest. Die Erde ruht zunächst im Zentrum des Koordinationsystems.
Earth = sphere(radius=6371e3, color=vector(0.0,0.5,1.0),
make_trail=True, trail_type='points', interval=5, retain=1000)
Earth.mass = 5.9724e24 # [kg]
Earth.pos = vector(0, 0, 0)
Earth.speed = vector(0, 0, 0)Der folgende Abschnitt ist nur aus einem softwaretechnischen Grund notwendig. GlowScript kann Texturen (im konkreten Fall die "Weltkarte" auf der Oberfläche der Erdkugel) derzeit grundsätzlich nur von einem Webserver, und nicht aus einer lokalen Datei laden. Der Code in diesem Abschnitt wartet drei Sekunden lang, ob sich die Textur laden lässt. Ansonsten wird die Erde ohne Textur als einfarbige blaue Kugel dargestellt. Sollte das trotz bestehender Internet-Verbindung passieren (z.B. weil diese ungewöhnlich langsam ist), könnte es evtl. sinnvoll sein, den Wert 30 (der drei Sekunden entspricht) in der Zeile "for i ..." etwas höher zu setzen.
scene.visible = False
Earth.texture = textures.earth
for i in arange(30):
rate(10)
if Earth.ready: break
if Earth.ready:
Earth.color=vector(1,1,1)
else:
Earth.texture = None
scene.visible = TrueDer folgende Abschnitt legt die Daten für den Satelliten fest. Der Radius des Satelliten (der keinen Einfluss auf den Bahnverlauf hat) ist zur besseren Sichtbarkeit unrealistisch auf 1000 km gesetzt. Der Parameter "retain" gibt an, wieviele Punkte des Schweifs des Satelliten -- der zur besseren Verfolgung der Bahn dient -- beibehalten werden, bis die ältesten Punkte gelöscht werden.
Satellite = sphere(radius=1000e3, color=color.gray(0.6),
make_trail=True, trail_type='points', interval=5, retain=1000)
Satellite.mass = 1000 # [kg]
Satellite.pos = vector(0, 0, Earth.pos.x+Earth.radius+Initial_Orbit)
Satellite.speed = vector(Initial_Speed, 0, 0)Der folgende Abschnitt definiert drei Buttons am unteren Rand der Animation. Mit dem ersten Button lässt sich die Animation unterbrechen und fortsetzen, mit dem zweiten Button mit der Beschriftung "Accelerate" lässt sich die Bahngeschwindigkeit des Satelliten um 5% erhöhen, und mit dem dritten Button mit der Beschriftung "Decelerate" lässt sich die Bahngeschwindigkeit des Satelliten um 5% verringern.
def Button_Pause(b):
global Running
Running = not Running
if Running:
b.text = ' Pause '
else:
b.text = 'Continue'
button(text=' Pause ', bind=Button_Pause)
def Button_Accelerate(b):
Satellite.speed = Satellite.speed * 1.05
button(text='Accelerate', bind=Button_Accelerate)
def Button_Decelerate(b):
Satellite.speed = Satellite.speed * 0.95
button(text='Decelerate', bind=Button_Decelerate)Der folgende Abschnitt definiert vier Textausgabefelder im unteren, linken Bereich der Animation. Im obersten Feld "Steps" wird die Zahl der durchgeführten Simulationsschritte angezeigt. Im nächsten Feld "Time" wird die in der Simulation abgelaufene Zeit angezeigt. Im nächsten Feld "Orbit" wird die Höhe des Orbits über der Erdoberfläche angezeigt. Um den Bahnradius (d.h. den Abstand der Schwerpunkte von Satellit und Erde) zu bestimmen, muss zu diesem Wert der Erdradius addiert werden. Im nächsten Feld "Speed" wird die Bahngeschwindigkeit des Satelliten angezeigt.
Label_Steps = label(pixel_pos=True, pos=vector(0, 110, 0), align='left', opacity=1,
color=color.green, box=False)
Label_Time = label(pixel_pos=True, pos=vector(0, 80, 0), align='left', opacity=1,
color=color.green, box=False)
Label_Satellite_Orbit = label(pixel_pos=True, pos=vector(0, 50, 0), align='left', opacity=1,
color=color.green, box=False)
Label_Satellite_Speed = label(pixel_pos=True, pos=vector(0, 20, 0), align='left', opacity=1,
color=color.green, box=False)In dem folgenden Abschnitt wird der Zähler für die Simulationsschritte (step) initialisiert, und die sehr wichtige Variable für die Zeitdauer eines einzelnen Simulationsschritts (dt) gesetzt. An dieser Stelle macht sich die Langsamkeit von VPython unangenehm bemerkbar. Um auch auf nicht allzu schnellen PCs eine brauchbare Geschwindigkeit zu erzielen, habe ich den Wert auf 100 Sekunden festgesetzt. In Bezug auf die Genauigkeit der Simulation wäre es allerdings eigentlich wünschenswert, den Wert sehr viel niedriger zu setzen. Für einfache Experimente mit der Simulation reicht der Wert 100 allerdings aus. Bei einem geostationären Orbit mit einer Umlaufzeit von ca. 86164 Sekunden wird die Bahn damit aus ca. 860 geraden Teilstücken zusammengesetzt.
step = 0
dt = 100In dem folgenden Abschnitt wird das automatische Zoomen abgeschaltet, und der sichtbare Bereich auf das Doppelte des von der Automatik bis dahin ermittelten Werts vergrössert. Bei Experimenten mit stark grössenveränderlichen Umlaufbahnen kann es u.U. sinnvoll sein, diesen Abschnitt auszukommentieren bzw. zu löschen.
scene.autoscale = False
scene.range = scene.range * 2Der folgende Abschnitt ist der Beginn der eigentlichen Simulationsschleife. Der Befehl rate(100) bewirkt, dass die Schleife nicht schneller als mit 1/100 Sekunde pro Durchlauf abgearbeitet wird. Dadurch wird eine einheitliche Ablaufgeschwindigkeit unabhängig von der Rechenleistung des Systems erreicht. Vorausgesetzt natürlich, das System ist schnell genug, um einen Schleifendurchlauf in nicht mehr als 1/100 Sekunde abzuarbeiten. Die "Running"-Variable wird durch den "Pause"-Button umgeschaltet. Solange "Running" auf False gesetzt ist, wiederholt sich nur dieser kleine Abschnitt der Schleife.
while True:
rate(100)
if not Running: continueDie folgende Zeile berechnet den Abstand der Schwerpunkte von Satellit und Erde. Intern werden dabei drei Werte (x/y/z) berechnet.
r = Satellite.pos - Earth.posDie folgende Zeile berechnet mit der üblichen Standardformel die gravitative Kraft zwischen Satellit und Erde. Intern werden dabei wiederum drei Werte (x/y/z) berechnet. Über norm(r) wird dabei die Richtung der Kraft ermittelt, der Rest des Ausdrucks ergibt den (richtungsunabhängigen) Absolutbetrag.
F = G * Earth.mass * Satellite.mass * norm(r) / mag(r)**2Die folgenden beiden Zeilen berechnen die Änderung der Geschwindigkeiten von Erde und Satellit auf Basis der in der vorhergehenden Zeile berechneten aktuell wirkenden Kraft. Intern werden dabei wiederum drei Werte (x/y/z) berechnet. Der entscheidende Punkt dabei ist, dass die Kraft für die Zeitdauer des Simulationsschritts (dt) als konstant angenommen wird. Im Gegensatz dazu ändert sich die Kraft in Realität laufend. Ist die Zeitdauer des Simulationsschritts angemessen kurz, ist die daraus resultierende Abweichung vernachlässigbar. Es ist leider, wie oben erwähnt, bei dieser Simulation aus Performancegründen nicht sinnvoll, die Zeitdauer eines Simulationsschritts so niedrig zu setzen, wie eigentlich wünschenswert wäre.
Earth.speed = Earth.speed + (F / Earth.mass) * dt
Satellite.speed = Satellite.speed - (F / Satellite.mass) * dtDie folgenden beiden Zeilen berechnen die Änderung der Positionen von Erde und Satellit auf Basis der in der vorhergehenden Zeile berechneten Geschwindigkeiten. Intern werden dabei wiederum drei Werte (x/y/z) berechnet. Die Geschwindigkeiten werden dabei, ähnlich wie die Kraft im vorhergehenden Abschnitt, für die Zeitdauer des Simulationsschritts als konstant angenommen. Es handelt sich also um eine stückweise geradlinige Bewegung. Für die Genauigkeit gilt entsprechend, was ich im vorhergehenden Abschnitt erläutert hatte. Es hat übrigens einen wichtigen und mathematisch ziemlich komplizierten Grund, warum erst die Geschwindigkeiten und danach die Orte neu berechnet werden (Stichwort:
Symplektisches Eulerverfahren). Die Genauigkeit der Simulation ist bei dieser Reihenfolge wesentlich besser, als wenn man zuerst die Orte neu berechnet.
Earth.pos = Earth.pos + Earth.speed * dt
Satellite.pos = Satellite.pos + Satellite.speed * dtDie folgenden beiden Zeilen drehen die Erdkugel entsprechend der Zeitdauer eines Simulationsschritts (aber nur, wenn die Textur erfolgreich geladen wurde, weil man sonst die Drehung sowieso nicht sehen kann).
if (Earth.texture != None):
Earth.rotate(axis=vector(0,1,0), (dt / Siderial_Day) * 2 * pi)Die folgenden Zeilen geben die oben beschriebenen aktuellen Werte für die Zahl der durchgeführten Simulationsschritte, die in der Simulation abgelaufene Zeit, und den Orbit und die Bahngeschwindigkeit des Satelliten aus.
Label_Steps.text='Steps: ' + (step + 1)
Label_Time.text='Time: '+ round((step + 1) * dt) + ' s'
Label_Satellite_Orbit.text='Orbit: ' + round(mag(r) - Earth.radius) + ' m'
Label_Satellite_Speed.text='Speed: ' + round(mag(Satellite.speed)) + ' m/s'Die letzte Zeile -- auch wenn sie eigentlich kaum eine Beschreibung braucht
;) -- erhöht den Zähler für die durchgeführten Simulationsschritte um 1:
step = step + 1Auch wenn die Genauigkeit der Simulation, wie erwähnt, aus Performancegründen nicht ganz so gut ist, wie ich mir gewünscht hätte, reicht sie für einfache Experimente mit Umlaufbahnen ohne weiteres aus. Unabhängig davon ist es natürlich auch möglich, den Parameter dt tatsächlich sehr viel niedriger (auch < 1 Sekunde) zu setzen, und die Genauigkeit damit entsprechend zu erhöhen. Die Simulation wird dann eben nur sehr langsam.
Grundsätzlich wird bei der Simulation nicht nur die Kraftwirkung der Erde auf den Satelliten, sondern auch die des Satelliten auf die Erde berechnet. Es sind also auch Simulationen möglich, bei denen sich die Erde deutlich bewegt (z.B. wenn man für den Satelliten die Daten des Mondes eingibt).
Das beschriebene Simulationsverfahren ist eines der einfachsten seiner Art, da es mir in diesem Fall insbesondere um möglichst gute Nachvollziehbarkeit ging. Es gibt erheblich leistungsfähigere Verfahren (z.B.
Runge-Kutta-Fehlberg), die u.a. mit adaptiven Schrittweiten arbeiten. Die Implementierung dieser Verfahren ist jedoch erheblich aufwändiger, und ihre Funktionsweise ist wesentlich schwerer zu verstehen.
Um die Animation nicht nur laufen zu lassen, sondern auch -- was ich anregen möchte -- selbst zu verändern, gibt es im wesentlichen zwei Möglichkeiten:
Zum einen die "Cloud"-Variante: Man kann sich kostenlos bei
glowscript.org registrieren ("Sign in" in der oberen rechten Ecke der Webseite). Das habe ich selbst allerdings nicht getan, und kann daher auch nichts näheres zu dieser Variante sagen. Ich vermute, dass die Benutzung so ähnlich wie bei den weiter oben verlinkten
Beispielprogrammen abläuft.
Zum anderen die lokale Variante:
1. Zunächst auf der
GlowScript-GitHub-Webseite die aktuelle GlowScriptOffline-Version herunterladen. Derzeit ist das die Datei
GlowScriptOffline3.0.zip. Nach diesem Schritt ist (ausser im Hinblick auf die weiter oben beschriebene Textur-Problematik) keine Internet-Verbindung mehr notwendig.
2. Als nächstes die heruntergeladene zip-Datei lokal in einem beliebigen Verzeichnis entzippen.
3. Nun in diesem Verzeichnis die Datei GlowScript.html starten (bzw. mit einem Webbrowser öffnen).
4. Nun sollte sich im verwendeten Webbrowser eine zweigeteilte Seite öffnen: Im linken Bereich der GlowScript-Sourcecode-Editor, und im rechten Bereich eine leere Fläche für die Grafik-Ausgabe.
5. Über den Browse-Button kann man nun ein GlowScript-Programm laden. Testweise bieten sich dazu die Demo-Programme im Unterverzeichnis Demo an. Sobald sichergestellt ist, dass die Installation sauber funktioniert, kann man dann die obige Datei Satellite_Simulation.py laden.
6. Mit dem Run-Button lässt sich (naheliegenderweise
;)) das geladene Programm starten.
7. Mit dem Export-Button lässt sich das Programm in eine HTML/JavaScript-Datei umwandeln, die unabhängig von der GlowScript-Offline-Installation funktionsfähig ist (allerdings eine Intenet-Verbindung zum Laden der Bibliotheken erfordert).
Nun zur eingangs erwähnten Frage, was geschieht, wenn man ein Objekt auf einer Kreisbahn beschleunigt oder abbremst. Zu diesem Zweck hat die Simulation die Buttons "Accelerate" (Beschleunigen: die aktuelle Bahngeschwindigkeit des Satelliten wird bei der Betätigung des Buttons um 5% erhöht) und "Decelerate" (Abbremsen: die aktuelle Bahngeschwindigkeit des Satelliten wird bei der Betätigung des Buttons um 5% vermindert). Bei einmaliger Betätigung des "Decelerate"-Buttons ergibt sich der folgende Bahnverlauf:
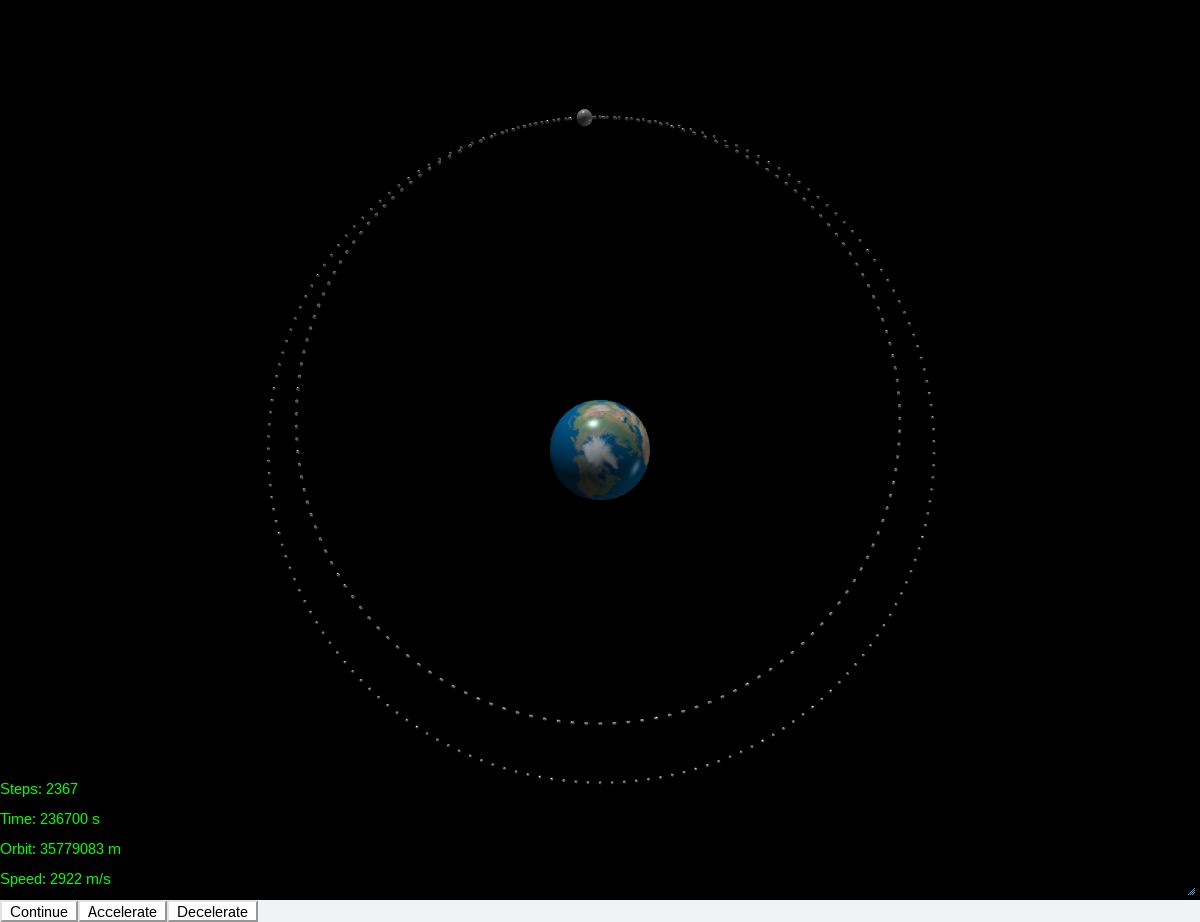
Die ursprüngliche Kreisbahn wird zu einer stabilen Ellipsenbahn, die sich (ohne Ausseneinfluss) nicht mehr weiter verändert. Das ist der Normalfall, und geschieht immer, sofern die Bahngeschwindigkeit nicht bestimmte Grenzwerte (die i.d.R. einer
erheblichen Beschleunigung bzw. Abbremsung entsprechen) über- bzw. unterschreitet.
Es ist auch gar nicht so schwer, zu verstehen,
warum aus einer Kreisbahn durch einen einmaligen Beschleunigungs- oder Abbremsvorgang i.d.R. eine stabile Ellipsenbahn wird:
1. Ellipsenbahnen sind im Prinzip genauso stabil wie Kreisbahnen. Das ist seit Keppler bekannt, und lässt sich auch mathematisch beweisen.
2. An den Scheitelpunkten einer Ellipsenbahn gibt es nur
einen einzigen Unterschied zu einer Kreisbahn, die durch den gleichen Punkt verläuft: Die Bahngeschwindigkeit ist entweder höher als bei einer Kreisbahn (das gilt für die Periapsis, den Scheitelpunkt, der sich näher am Zentralobjekt befindet) oder niedriger als bei einer Kreisbahn (das gilt für die Apoapsis, den Scheitelpunkt, der sich weiter entfernt vom Zentralobjekt befindet).
3. Ändert sich an einem Bahnpunkt einer Kreisbahn die Bahngeschwindigkeit, so ist die Bahn ab diesem Punkt identisch mit einer Ellipsenbahn, die diesen Bahnpunkt als Scheitelpunkt, und dort die gleiche Bahngeschwindigkeit hat. Die Kreisbahn geht unmittelbar in diese Ellipsenbahn über. Es gibt nach der Geschwindigkeitsänderung ab diesem Punkt keinen Unterschied in den Bahnverläufen mehr.
4. Die neue Ellipsenbahn ist gemäss Punkt 1. stabil.
Möchte man -- was in der Praxis häufig der Fall ist -- aus der neuen Ellipsenbahn wieder eine Kreisbahn, aber auf höherem oder niedrigerem Orbit machen, so ist eine
zweite Beschleunigung bzw. Abbremsung erforderlich. Dazu muss man an dem entsprechenden Scheitelpunkt der Ellipsenbahn die Bahnschwindigkeit so ändern, dass sie der Bahngeschwindigkeit einer Kreisbahn mit diesem Bahnradius entspricht (entsprechend der weiter oben angegebenen Formel). Diese zweifache Geschwindigkeitsänderung, um von einer Kreisbahn auf eine andere Kreisbahn zu wechseln, wird als
Hohmann-Transfer bezeichnet.











