Der Satellit im freien Fall

skagerak schrieb:Ich dachte eher theoretisch und praktisch nicht.

Theoretisch ist immer alles möglich, solange es nicht praktisch falsifiziert wurde ...

schukoplex schrieb:Theoretisch ist immer alles möglich, solange es nicht praktisch falsifiziert wurde ...

Ja, okay :D, in diesem Sinne ist es wohl theoretisch möglich. Aber die Theorien dazu auf die Realität bezogen (meinetwegen rechnerisch), da ist es nicht möglich, oder?

Thaddeus schrieb:Relativ zur Mondoberfläche schon. Aber versuch' dann mal, zur Erde zu kommen. Dann wird das Vorbeifallen nämlich lästig.

Sind irgendwas um die 3600 Stundenkilometer.

Nach deinem letzten Edit denke sich zu begreifen, worauf du hinaus willst. Du gehst von ausgedehnten Objekten, also "Körpern" aus, ich hingegen nur von "punktförmigen Massepunkten" (...). Wenn also ein solcher Punkt sich auf einer exakten Kreisbahn um einen anderen Punkt herum bewegte - wie könnte man dann irgendeine "Geschwindigkeit" festlegen?

@schukoplex

Du mißt den Abstand zu den Ding, das Du umkreist. Dann mißt Du die Zeit, die Du brauchst, um einmal rundrum zu gelangen. Wenn's da jetzt natürlich gar keine optischen Anhaltspunkte gibt, dann mußt Du gebildetere Leute als mich fragen. Bei mir gibt's immer ganz viel Universum, an dem man sich optisch festhalten kann.

@schukoplex:

schukoplex schrieb:Wenn ich mich (z.B. als Mond) mit absolut konstanter Winkelgeschwindigkeit um den Massenmittelpunkt der Erde bewegen würde (also eben auf einer idealen Kreisbahn), wäre ich doch in beiden Bezugssytemen schwerelos, also unbeschleunigt, ...

Jede nicht-gleichförmig-geradlinige (anders formuliert: der Trägheit zuwiderlaufende) Bewegung gilt als beschleunigt (wobei die Beschleunigung auch negativ, d.h. eine Abbremsung sein kann). Z.B. bei einer Kreisbahn wird der Satellit laufend in Richtung der Erde beschleunigt, und in Richtung der Tangentialbahn abgebremst. Beides gleicht sich so aus, dass die Bahngeschwindigkeit bezogen auf die Kreisbahn konstant bleibt.

Das war eines der ursprünglichen zentralen Argumente gegen das Bohrsche Atommodell: Elektronen, die sich auf einer Kreisbahn bewegen, sind -- wie oben beschrieben -- laufend beschleunigt, und beschleunigte Ladungen strahlen elektromagnetische Wellen ab. Daher müssten Elektronen, die sich auf einer Kreis- (oder auch Ellipsen-) Bahn um den Atomkern bewegen, laufend elektromagnetische Wellen abstrahlen, dadurch Energie verlieren, und in den Kern stürzen. Das ist einer der Gründe, warum man von dem "anschaulichen" Elektronen-kreisen-um-den-Kern-Modell ziemlich bald wieder abgekommen ist.

uatu schrieb:Jede nicht-gleichförmig-geradlinige (anders formuliert: der Trägheit zuwiderlaufende) Bewegung gilt als beschleunigt (wobei die Beschleunigung auch negativ, d.h. eine Abbremsung sein kann).

Ein Satellit auf einer exakt kreisförmigen Umlaufbahn würde keinerlei Beschleunigung "spüren", aus "seiner Sicht" wäre er immer exakt geradeaus unterwegs; diese Ansicht würde noch dadurch bestärkt, dass er ständig parallel zu einer Fläche unter ihm unterwegs ist. Das würde sogar physikalisch stimmen.

Und was die Atommodelle betrifft - ich finde mitterweile schon das "Orbitalmodell" als zu wenig abstrakt.

delta.m schrieb:Ich habe mir das mal mit dem "Fallen" bzw. "Vorbeistürzen" versucht, vektoriell vorzustellen:

Wieso issn bei Dir der zweiteblaue Pfeil, der linke, länger gezeichnet als der erste? Klar, die Fallbeschleunigung ist ja ne Beschleunigung. Und wenn ein Objekt lotrecht fällt, kommt das auch hin.

Aber Dir müßte doch schon mal auffallen, daß der zweite blaue Pfeil nicht in die selbe Richtung zeigt wie der erste. Nicht nach unten (auf der Grafik), sondern nach rechts unten.Wie soll denn die mit dem ersten blauen Pfeil erzeugte "Bewegung nach unten" sich nun gedreht haben, daß sie nun nach schräg rechts unten verläuft und also zum nächsten normal langen blauen Pfeil hinzuaddiert wird? Geht doch nicht.

Tatsächlich darfst Du den ersten blauen Pfeil gar nicht mehr irgendwo hinzuaddieren, da Du ihn ja schon längst hinzuaddiert hast. Nämlich zum ersaten grünen Pfeil. Er steckt also schon im ersten roten Pfeil drin. Die Kraft des blauen Pfeils wurde also exakt "aufgebraucht" und führte zur Richtungsänderung.

Nun würde das Objekt wieder in Richtung des zweiten grünen Pfeils fliegen wollen, mit gleicher Geschwindigkeit wie am Anfang (die Beschleunigung des Freien Falls ging ja quasi für die Richtungsänderung drauf). Nun muß er zweite blaue Pfeil genauso lang sein wie der erste, und wieder zum Erdmittelpunkt zeigen. Damit findet hier dann dasselbe wie zuvor statt.

Die Fliehkraft ist keine Kraft, die dem blauen Pfeil entgegengesetzt ist, sondern die Trägheit des Objektes, welches auf dem grünen Pfeil entlang fliegen will, aber auf den roten Pfeil gezwängt wird. Würde ein Objekt sich auf einem solchen Orbit bewegen, und würde durch irgendeine Magie der umkreiste Planet verschwinden, würde die FLiehkraft das Objekt nicht in die entgegengesetzte Richtung des blauen Pfeils wegfliegen lassen, sondern schlicht in Richtung des grünen Pfeils. Weil eben die Kaft, die der grüne Pfeil darstellt, die einzige wirkende Kraft ist, die dem freien Fall inRichtung blauer Pfeil entgegenwirkt.

Daher vergiß die zweite Grafik mit dem Fliehkraftpfeil, der dem Pfeil in Richtung Erdmittelpunkt entgegengesetzt eingezeichnet ist.

@uatu
Nochmals, genauer überlegt, ist das mit der "Fläche" freilich falsch. Sollte besser "Punkt" lauten.

@schukoplex:

schukoplex schrieb:Ein Satellit auf einer exakt kreisförmigen Umlaufbahn würde keinerlei Beschleunigung "spüren", aus "seiner Sicht" wäre er immer exakt geradeaus unterwegs; diese Ansicht würde noch dadurch bestärkt, dass er ständig parallel zu einer Fläche unter ihm unterwegs ist.

Es ist relativ einfach möglich, auch ohne Aussenbeobachtung eine geradlinige Bewegung von einer Bewegung auf einer Kreisbahn zu unterscheiden: mit einem Kreisel. Damit lassen sich -- ausreichende Präzision vorausgesetzt -- alle richtungsändernden Beschleunigungen genau ermitteln.

@perttivalkonen

perttivalkonen schrieb:Wieso issn bei Dir der zweiteblaue Pfeil, der linke, länger gezeichnet als der erste? Klar, die Fallbeschleunigung ist ja ne Beschleunigung. Und wenn ein Objekt lotrecht fällt, kommt das auch hin.

Aber Dir müßte doch schon mal auffallen, daß der zweite blaue Pfeil nicht in die selbe Richtung zeigt wie der erste. Nicht nach unten (auf der Grafik), sondern nach rechts unten.Wie soll denn die mit dem ersten blauen Pfeil erzeugte "Bewegung nach unten" sich nun gedreht haben, daß sie nun nach schräg rechts unten verläuft und also zum nächsten normal langen blauen Pfeil hinzuaddiert wird? Geht doch nicht.

Tatsächlich darfst Du den ersten blauen Pfeil gar nicht mehr irgendwo hinzuaddieren, da Du ihn ja schon längst hinzuaddiert hast. Nämlich zum ersaten grünen Pfeil. Er steckt also schon im ersten roten Pfeil drin. Die Kraft des blauen Pfeils wurde also exakt "aufgebraucht" und führte zur Richtungsänderung.

Diese Zeichnung war mein erster Versuch, also sei nich so streng :)


Alle Pfeile sind zurückgelegte Wege pro gleicher Zeiteinheit (z.B. dt=1 sec).

Der erste kurze blaue Pfeil ist die Strecke, die der Körper in der Zeit dt = 0 bis 1 sec zurücklegen würde wenn er einfach fallengelassen würde.

Der zweite längere blaue Pfeil beschreibt die Strecke, die er zw. sec 1 und sec 2 zurücklegt. Diese Strecke ist natürlich länger als zw. sec 0 bis sec 1.


Der blaue Vektor (=Erdanziehung) zeigt immer zum Erdmittelpunkt).

Den Rest Deines Beitrags muß ich erst noch genauer überdenken ...

...aber nicht mehr heute :)

gn8

@delta.m:

delta.m schrieb:Der zweite längere blaue Pfeil beschreibt die Strecke, die er zw. sec 1 und sec 2 zurücklegt. Diese Strecke ist natürlich länger als zw. sec 0 bis sec 1.

An der Stelle stimmt's nicht. Wie schon mal erwähnt, ist die Situation von 1..2 s vollkommen symmetrisch zu der von 0..1 s: Die Bahngeschwindigkeit ist gleich, der Abstand zum Mittelpunkt der Zentralmasse ist gleich, etc. Also resultiert auch die gleiche Bewegung (relativ zur Zentralmasse).

delta.m schrieb:Der zweite längere blaue Pfeil beschreibt die Strecke, die er zw. sec 1 und sec 2 zurücklegt. Diese Strecke ist natürlich länger als zw. sec 0 bis sec 1.

Eben nicht. Das habe ich ja zu erklären versucht.

Im lotrechten freien Fall führt die Beschleunigung der ersten Sekunde dazu, daß ein Objekt sich 9,81m tiefer befindet und sich mit 9,81m/s in Richtung Erde bewegt. Während der zweiten Sekunde wird das Objekt nochmals beschleunigt, fällt weitere 19,62m mit entsprechenden 19,62m/s Geschwindigkeit.

Beim "Freien Fall um die Erde" passiert nun aber eine Richtungsänderung. Das führt dazu, daß das Objekt nach einer Sekunde nicht 9,81m näher an die Erde gekommen ist und sich nicht mit 9,81m/s der Erde nähert. Daher kann hier auch nichts hinzuaddiert werden; der blaue Pfeil wird nicht länger.

Stell es Dir so vor. Eine Rakete fliegt an der Erde vorbei. Irgendwann ist sie der Erde am nächsten. Das ist auf Deinem ersten Bild der Punkt, wo der erste grüne Pfeil anfängt. Würde die Rakete nun weiter geradeaus fliegen, würde sie sich immer weiter von der Erde entfernen. Die Spitze des grünen Pfeils ist nun mal weiter vomErdmittelpunkt entferntals der Anfang dieses Pfeiles. Würde die Rakete ohne Antrieb liegen, also nur "aus Trägheit", dann würde sie in Richtung Erdmittelpunkt fallen. Aber sie würde eben auch in Richtung des grünen Pfeils weiterfliegen. Beide Bewegungen ergeben eine neue Bewegung. Das Sichvondererdeentfernen und das Sichdererdenähern heben einander auf. Die gerade Flugnahn wird durch den FreienFall zur Kreisbahn. Annäherung an die Erde Null, Wegflug von der Erde ebenfalls Null.

uatu schrieb:Es ist relativ einfach möglich, auch ohne Aussenbeobachtung eine geradlinige Bewegung von einer Bewegung auf einer Kreisbahn zu unterscheiden: mit einem Kreisel.

Noch mal schnell "gegengemeckert". Ein Kreisel ist ebenfalls ein räumlich ausgedehntes Objekt; ich wollte letztlich darauf hinaus, ob sich zwei Punkte ("punktförmige Objekte"), welche sich - von außen betrachtet - "radial" umeinander mit stets exakt gleichem Abstand zueinander ("perfekte Kreisbahn") bewegen, tatsächlich zueinander bewegen.

Aber den Kreisel nehme ich jetzt gern mit ins Bett, als "Einschlafhilfe".

Oh, kurze Frage noch: Wie schnell darf, kann oder muss sich denn dieser Kreisel drehen?

schukoplex schrieb:Ein Satellit auf einer exakt kreisförmigen Umlaufbahn würde keinerlei Beschleunigung "spüren", aus "seiner Sicht" wäre er immer exakt geradeaus unterwegs

Warum sollte er keine Beschleunigung spüren? Und warum wäre er aus seiner Sicht geradeaus unterwegs? Sollte er sich dann nicht eher als ruhend wahrnehmen?

schukoplex schrieb:Oh, kurze Frage noch: Wie schnell darf, kann oder muss sich denn dieser Kreisel drehen?

Da der Drehimpuls (in Betrag und Richtung) eine Erhaltungsgröße ist, ist es prinzipiell egal, wie schnell er sich dreht.

schukoplex schrieb:tatsächlich zueinander bewegen.

Was ist denn für dich eine tatsächliche Bewegung?

@delta.m: Es ist möglich, die Zentrifugalbeschleunigung (entsprechend der Fliehkraft) direkt aus der Trägheit herzuleiten. Das ist eine ungewöhnliche Art der Herleitung, die ich in dieser Form noch nicht gesehen habe. "Neu" ist sie allerdings sicherlich nicht. Mathematische Feinheiten lasse ich aus Zeitgründen beiseite. Zu Erläuterung zunächst eine Zeichnung:



Ohne die Anziehungskraft der Zentralmasse würde sich ein umlaufender Satellit ab dem Punkt X mit der Bahngeschwindigkeit v auf der mit z bezeichneten Strecke tangential weiterbewegen. Am Endpunkt der Strecke z hätte er sich um die Strecke d weiter vom Mittelpunkt der Zentralmasse entfernt, als der Kreisbahn entsprechen würde.

Diese Abweichung um die Strecke d von der Kreisbahn entspricht einer bestimmten Radialbeschleunigung. Sofern man einen sehr kleinen Zeitraum betrachtet, kann man diese Radialbeschleunigung als konstant annehmen. Sie ergibt sich dann aus der bekannten Formel für die bei einer gleichmässigen Beschleunigung zurückgelegten Wegstrecke:



Die Zeit t für das Durchlaufen der Strecke z (und damit auch die Zeit für die Entfernung um die Strecke d von der Kreisbahn) ergibt sich ganz einfach zu :



Die Gesamtentfernung r+d vom Mittelpunkt der Zentralmasse lässt sich einfach nach Pythagoras berechnen:



Für die Strecke d folgt daraus:



Die gewonnenen Ausdrücke für t und d kann man jetzt in die obige Formel für die Radialbeschleunigung a einsetzen:



Interessant ist nun, was sich daraus ergibt, wenn man die Strecke z (und damit auch den Zeitraum t) sehr klein werden lässt. Der Faktor v² ist für die Grenzwertbildung nicht relevant, weshalb ich ihn vorübergehend beseite lasse. Es geht also um die Bildung von:



Dazu erweitere ich den Bruch zunächst mit (der Grund wird im darauffolgenden Schritt klar):





Durch Anwendung der Formel (a-b)*(a+b)=a²-b² vereinfacht sich der Zähler des Bruchs erheblich:



Weiteres Vereinfachen ergibt:



Es ist nun leicht zu erkennen, was sich ergibt, wenn z immer kleiner wird:



Dieses Resultat kann man jetzt in die obige Formel für die Radialbeschleunigung a einsetzen:



Das ist aber genau die Formel für die Zentrifugalbeschleunigung (bzw. multipliziert mit der Masse m für die Zentrifugal- oder Fliehkraft). Das meinte ich, als ich weiter oben schrieb:

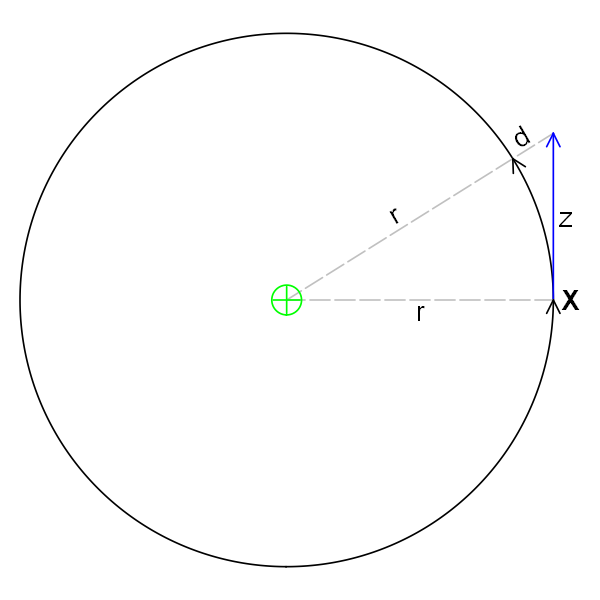
uatu schrieb:Die Fliehkraft ist äquivalent dazu, dass der Satellit trägheitsbedingt tangential geradeaus fliegen "möchte". Das sind zwei verschiedene Sichtweisen des gleichen Sachverhalts.

uatu schrieb:Es ist möglich, die Zentrifugalbeschleunigung (entsprechend der Fliehkraft) direkt aus der Trägheit herzuleiten. Das ist eine ungewöhnliche Art der Herleitung, die ich in dieser Form noch nicht gesehen habe. "Neu" ist sie allerdings sicherlich nicht.

Nicht nur nicht neu, sondern auch überhaupt nicht ungewöhnlich.

Die Zentrifugalkraft (von lateinisch centrum, Mitte und fugere, fliehen), auch Fliehkraft, ist eine Trägheitskraft, die bei Dreh- und Kreisbewegungen auftritt und radial von der Rotationsachse nach außen gerichtet ist. Sie wird durch die Trägheit des Körpers verursacht.
[...]
Die Zentrifugalkraft ist eine Scheinkraft und genügt daher nicht dem Prinzip von Actio und Reactio.

Wikipedia: Zentrifugalkraft

Trägheitskraft und Zentripetalkraft sind die beiden einzigen Kräfte, die da "wirklich wirken".

@perttivalkonen

perttivalkonen schrieb:Im lotrechten freien Fall führt die Beschleunigung der ersten Sekunde dazu, daß ein Objekt sich 9,81m tiefer befindet und sich mit 9,81m/s in Richtung Erde bewegt. Während der zweiten Sekunde wird das Objekt nochmals beschleunigt, fällt weitere 19,62m mit entsprechenden 19,62m/s Geschwindigkeit.

Geschwindigkeit und Position bzw. zurückgelegte Strecke haben nicht die gleichen Zahlenwerte bei einer beschleunigten Bewegung. D.h. bei konstanter Beschleunigung nimmt die Geschwindigkeit linear zu während die zurückgelgte Strecke quadratisch zunimmt.

Die Beschleunigung im Gravitationspotential ist gegeben durch (In einem Koordinantensystem das zur Richtung Erde zeigt):



Die Geschwindigkeit zum Zeitpunkt t erhält man dann durch:



Nach einer Sekunde ist die GEschwindigkeit daher 9,81 m/s und nach zwei Sekunden 19,62 m/s.

Die zurückgelegte Strecke erhält man dann durch:




Nach einer Sekunde ist die zurückgelegte Gesamtstrecke daher 4,91 m und nach zwei Sekunden ist die zurückgelegte Gesamtstrecke 19,62 m. Das heißt zwischen der ersten und der zweiten Sekunde legt das Objekt 19,62 m - 4,91 m = 14,71 m zurück.

@perttivalkonen:

perttivalkonen schrieb:Nicht nur nicht neu, sondern auch überhaupt nicht ungewöhnlich.

Natürlich wird die Zentrifugalkraft durch die Trägheit verursacht. Darum ging es nicht. Ich schrieb, dass die Herleitung in der Form, wie ich sie beschrieben habe, ungewöhnlich ist. Zumindest habe ich sie in dieser Form noch nicht gesehen, obwohl sie, wie ich erwähnte, sicherlich nicht neu ist.

@mojorisin
thx für die klärenden Worte. Ob Du's glaubst oder nicht, seit der Schule hab ich das so verstanden wie oben dargestellt. Und so oft ich davon sprach und es auch so darlegte, auch hier im Forum, warst Du heut der erste, der das mal angesprochen hatte.
Danke nochmal.