Glaubt ihr, dass es Außerirdische gibt?

Man sollte hier immer klar ausdrücken meint man die Wahrscheinlichkeit für leben im Universum oder leben nicht auf der Erde im Universum.

Für mich ist hier aber immer noch die einzige logische anwedung für Wahrscheinlichkeit. Dass beobachtbare Universum betrachten und dann möglichst exakt Parameter für die Entstehung von Leben festlegen.

Dies wurde auch von verschiedenen Forschern Physikern Mathematikern gemacht. Und die Resultate gehen von „schon die Erde ist unwahrscheinlich“ bis hinzu weiteres Leben ist fast sicher.

Ich denke weiterkommt man da auch nicht. Diese Parameter werden vllt besser bestimmt und wir beobachten mehr aber die Wahrscheinlichkeit bleibt bis zur wirklichen Entdeckung von lebennimmer kleiner 1.

Und hier nochmal ein Beispiel warum auch in einem unendlichen sich nicht wiederholendem Universum in dem es leben gibt nicht zwangsläufig ein zweites Mal leben geben muss.

Nehmen wir die Erde als Binärcode 101

Und betrachten dann die Zahlenfolgen

101 1001 10001 100001 … so haben wir eine unendliche nicht periodische zahlen folge in der 101 nur dieses eine mal vorkommt

continuum schrieb:Auch wenn in 40 Lichtjahren als beispiel ein erdähnlicher planet gefunden würde, wäre der in heutiger Sicht unmöglich in den nächsten paar Jahren bemannt zu erreichen.

Wie unser altbekannter Erich von Däniken aufgezeigt hat, wäre es mit sg. "Generationenraumschiffen" möglich, die mehrere hundert Jahre unterwegs sind , wo gelebt , gearbeitet wird , gestorben wird und neu geboren wird. Natürlich müssten sich dafür gute Familien finden lassen aber der menschliche Wille ist unermesslich, möglich wäre es imo

gagitsch schrieb:continuum schrieb:
Auch wenn in 40 Lichtjahren als beispiel ein erdähnlicher planet gefunden würde, wäre der in heutiger Sicht unmöglich in den nächsten paar Jahren bemannt zu erreichen.
Voyager als derzeit schnellstes Objekt aus Menschenhand würde so ca 700.000 Jahre benötigen.

rainlove schrieb:continuum schrieb:
Auch wenn in 40 Lichtjahren als beispiel ein erdähnlicher planet gefunden würde, wäre der in heutiger Sicht unmöglich in den nächsten paar Jahren bemannt zu erreichen.
Wie unser altbekannter Erich von Däniken aufgezeigt hat, wäre es mit sg. "Generationenraumschiffen" möglich, die mehrere hundert Jahre unterwegs sind , wo gelebt , gearbeitet wird , gestorben wird und neu geboren wird. Natürlich müssten sich dafür gute Familien finden lassen aber der menschliche Wille ist unermesslich, möglich wäre es imo

Ja, das habe ich mir auch schon gedacht, aber dann müsste es schon fast ein Raumschiff der Grösse eines Planeten sein im Sinne einer Wirtschaft, siehe das von Perttivalkonen (O'Neil Zylinder, oder ähnliches), damit man das überbrücken könnte so von der Aussage von @gagitsch mit den ca. 700.000 Jahre, auch wenn wir mal 10x schneller fliegen könnten, dann ist es immer noch schnurrgerade 70.000 Jahre, einfach unheimlich.

Hier das Video:
Gibt schon bessere und andere, aber egal.

Rama - HQ version

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Noumenon schrieb:Eine Wahrscheinlichkeit von exakt 0 bedeutet in diesem Fall nun einmal, dass ein Ereignis niemals eintritt, auch nicht bei unendlich vielen Versuchen.

perttivalkonen schrieb:Nope, das heißt es nur im Falle endlicher Events. Bei unendlich vielen Events, aber nur endlich vielen Eintreffen eines bestimmten Ergebnisses kann die Wahrscheinlichkeit des Auftretens dieses Ergebnisses nicht >0 heißen.

Wie gesagt, ein endlicher Wert aus unendlichen Events, dessen Wahrscheinlichkeit geht gegen Null. Kannst auch gerne "ist exakt Null" sagen, kommt ja aufs selbe hinaus. Zätz ze probläm - wie ja auch bei 1=2 weil 1x[unendlich]=2x[unendlich] Da haste Recht, inner Mathematik spricht mans nicht so gerne aus, aber das Limesproblem bleibt nun mal. Und ist verdammt real, sobald wir ein unendliches Universum voraussetzen.

Da verwechselst du relative Häufigkeit mit Wahrscheinlichkeit. Wenn du 3x Lotto spielst und 1x gewinnst, liegt die relative Häufigkeit des Gewinns bei 1/3, aber daraus folgt nicht, dass auch die Wahrscheinlichkeit bei 1/3 liegt.

perttivalkonen schrieb:Nur bei einem endlich großen Teiler beweist ein Event, daß dessen Auftretenswahrscheinlichkeit über der Null liegen muß. Bei einem unendlich großen Divisor führt selbst ein immens großer, jedoch endlicher Wert als Dividend nicht zu >0 als Ergebnis.

Noumenon schrieb:Ja, diese "Logik" basiert halt auf einer klassischen Milchmädchenrechnung bzw. der falschen Anwendung von Grenzwerten und Wahrscheinlichkeitskonzepten. Wahrscheinlichkeiten werden durch Wahrscheinlichkeitsmaße definiert, nicht durch einfache Division auf Basis einer Milchmädchenrechnung.

perttivalkonen schrieb:Sagt der, der auf die Ermittlung des Wahrscheinlichkeitswertes für Leben schei*t und gleich die Gesamtwahrscheinlichkeit für Leben im Universum festlegt, weil "uns gibts ja", also ist n/X > 0, weil n mindestens 1.

Wie gesagt: Die Wahrscheinlichkeit definiert sich nicht durch einfache Division auf Basis einer Milchmädchenrechnung (dein "n/X"). Hättest du recht, wäre das ein klarer Widerspruch zum Wahrscheinlichkeitsbegriff. Nehmen wir als Beispiel die natürlichen Zahlen, ziehen eine x-beliebige Zahl und fragen uns, wie hoch die Wahrscheinlichkeit gewesen ist, diese konkrete Zahl (bspw. 42) gezogen zu haben. Jetzt sagst du: Null! Deine Begründung: 1/Unendlich = 0, ein einzelnes Ergebnis geteilt durch unendlich viele Möglichkeiten ergäbe eben Null (deine Milchmädchenrechnung). So weit, so gut. Wäre aber für alle möglichen Zahlen die Wahrscheinlichkeit exakt 0, diese Zahl zu ziehen, würden sich alle Wahrscheinlichkeiten zu 0 aufsummieren, im Widerspruch zu Forderung, dass sich alle Wahrscheinlichkeiten zu 1 aufsummieren müssen. Und damit ist eben ausgeschlossen, dass p für alle Zahlen exakt 0 ist.

perttivalkonen schrieb:War ja auch meine Folgerung, daß diese Umkehr aufs selbe hinausläuft, was Du gesagt hast. Daß Du auch noch auf eine Verschiedenheit zwischen stetiger und diskreter Warhscheinlichkeit verweist, ist dabei geschenkt, solange Du Null Aufweis erbringst, daß dieser Unterschied für das hiesige Problem relevant ist (is ja nich so, als ob da alles verschieden wäre, etwa das Problem von [endlicher Wert] / [unendlicher Wert] worauf ich mich ja bezogen hatte.

Ja, der Unterschied ist schon relevant, schließlich sind Planeten abzählbar.

perttivalkonen schrieb:Zeig doch mal bitte, daß es falsch ist, daß der Wert 1/n sich bei ständiger Erhöhung von n der Null nähert, wie sich n dem Unendlich nähert. Anders ausgedrückt: sobald jemand daherkommt und n direktemang auf [unendlich] setzt (Universum unendlich), der Wert 1/n genauso direktemang bei 0 landet.

Nein, das ist so schon richtig, wurde aber auch nicht bestritten.

perttivalkonen schrieb:Vielleicht merkste's ja irgendwann mal, daß ich mich in der damaligen Diskussion einzig dagegen gewehrt hatte, die Wahrscheinlichkeit für Leben im Universum nicht über die Bestimmung des Wahrscheinlichkeitswertes zu bestimmen, sondern einfach aus "uns gibts ja, und wenns Universum unendlich is, dann". Wenn also jemand nur auf die Gesamtwahrscheinlichkeit schaut und bei so ner Limesrechnung sagt "muß >0 sein", dann halt ich dem ein genauso definites "muß =0 sein" entgegen.

Ich habe die Diskussion zwar nicht mitverfolgt, aber sie kommt ja immer wieder mal auf, alle paar Wochen, Monate oder Jahre. Und wir wissen nun einmal, dass Leben endstanden ist, damit kann die Wahrscheinlichkeit eben nicht bei Null liegen so wie bspw. für die Entstehung einer Boeing 747, wenn ein Tornado über einen Schrottplatz fegt (der kann da auch unendlich oft über den Schrottplatz fegen, es wird keine Boeing 747 dabei herauskommen).

perttivalkonen schrieb:Ansonsten kannste's Dir auch sparen, hier nochmal was zu zu schreiben - wenn nichts wirklich Neues hinzu kommt. Schlichtes Wiederholen mit anderen Worten bringts nicht. Danke.

Da hier insbesondere auf der letzten bzw. mittlerweile vorletzten Seite (1.111) wild über Unendlichkeiten sinniert wurde, ohne zu einem vernünftigen Ergebnis zu kommen, macht eine Klarstellung schon Sinn.

---

Donidoni2 schrieb:Und hier nochmal ein Beispiel warum auch in einem unendlichen sich nicht wiederholendem Universum in dem es leben gibt nicht zwangsläufig ein zweites Mal leben geben muss.

Nehmen wir die Erde als Binärcode 101

Und betrachten dann die Zahlenfolgen

101 1001 10001 100001 … so haben wir eine unendliche nicht periodische zahlen folge in der 101 nur dieses eine mal vorkommt

Wenn Vergleiche hinken, ist ja schon schlimm, aber wenn sie förmlich auf dem Bauch kriechen...? Dein Beispiel ist deterministisch, konstruiert, welches eine Ausnahme künstlich erzwingt, indem es explizit vorgibt, wo genau "101" vorkommen darf. Ein Universum mit zufälligen, aber wiederholbaren physikalischen Prozessen funktioniert probabilistisch: Wenn es in einem Teil des Universums Bedingungen gibt, die zur Entstehung von Leben (oder anderer Naturphänomenen) führen, gibt es keinen Grund, warum diese Bedingungen nicht auch an anderer Stelle reproduzierbar sein und in einem unendlich großen Universum sogar unendlich oft vorkommen sollten. Alle Gegen"argumente" sind konstruiert a la "Die Zahl 42 gibt's ja trotz unendlich vieler Zahlen auch nur ein einziges Mal!"

---

continuum schrieb:Ja, das habe ich mir auch schon gedacht, aber dann müsste es schon fast ein Raumschiff der Grösse eines Planeten sein im Sinne einer Wirtschaft, siehe das von Perttivalkonen (O'Neil Zylinder, oder ähnliches), damit man das überbrücken könnte so von der Aussage von @gagitsch mit den ca. 700.000 Jahre, auch wenn wir mal 10x schneller fliegen könnten, dann ist es immer noch schnurrgerade 70.000 Jahre, einfach unheimlich.

Naja, ich verfolge das zwar nur am Rande mit, aber in der Schublade stecken weitaus effizientere Antriebssysteme, etwa winzige Sonden, die durch Laserlicht beschleunigt und auf eine Reisezeit von ~20 Jahren bis Proxima Centauri b kommen könnten:
https://www.nasa.gov/general/swarming-proxima-centauri/

Ausführlicher (Video vom 2. Januar 2025, ca. 20min):

NASA is embarking on an extraordinary mission to Proxima Centauri b, a distant exoplanet that lies just 4.2 light-years away from Earth. Situated in the habitable zone of its star, Proxima Centauri b could hold the key to finding life beyond our planet. But how will NASA overcome the immense challenges of interstellar travel?

In this video, we dive deep into the technological advancements that could make this mission a reality, including the use of laser-powered lightsails and autonomous picospacecraft swarms. Discover how these groundbreaking technologies will allow us to explore one of the most promising candidates for extraterrestrial life.

We also explore the ethical dilemmas and international cooperation required for such an ambitious mission. Will we find signs of life on Proxima Centauri b, or will the mission reveal more about the mysteries of space than we ever imagined?

NASA Is Planning A Mission To Proxima B And It Could Change Everything!

Externer Inhalt
Durch das Abspielen werden Daten an Youtube übermittelt und ggf. Cookies gesetzt.

Noumenon schrieb:Naja, ich verfolge das zwar nur am Rande mit, aber in der Schublade stecken weitaus effizientere Antriebssysteme, etwa winzige Sonden, die durch Laserlicht beschleunigt und auf eine Reisezeit von ~20 Jahren bis Proxima Centauri b kommen könnten:
https://www.nasa.gov/general/swarming-proxima-centauri/

Danke für den Link.

Ja, das habe ich auch schon gehört. Ich finde das eine sehr schöne Idee.
Hoffe das die umgesetzt wird. ;)

Das Faszinierende ist, wenn sie für die etwa 4,5 Lichtjahre beschleunigt werden, müsste die Beschleunigung ungefähr 90% betragen und der Zeitpunkt festgelegt werden, ab dem die Sonden wieder abbremsen sollten. Ich gehe davon aus, dass es dann trotzdem etwa 6 Lichtjahre oder mehr dauern würde, aber es wäre immer noch plausibel zu erreichen (wegen der Beschleunigung und wegen dem abbremsen).

Das andere ist, dass wir zurzeit und wahrscheinlich auch in den nächsten 20 Jahren nicht in der Lage sein werden, unsere Antriebe für bemannte Flüge auf etwa 10% der Lichtgeschwindigkeit zu bringen, aber man weiß ja nie.

Proxima Centauri wäre daher ideal zu erreichen. Nehmen wir an, wir brauchen insgesamt 7,5 Lichtjahre mit beschleunigen und abbremsen, dann würde ein Raumschiff mit einem Zehntel der Lichtgeschwindigkeit 75 Jahre benötigen, was mit einem Generationsraumschiff durchaus machbar wäre. Also so prophylaktisch geschaut.

continuum schrieb:etwa 6 Lichtjahre oder mehr dauern würde

continuum schrieb:brauchen insgesamt 7,5 Lichtjahre

Ein Lichtjahr ist eine Entfernungseinheit, keine Zeiteinheit. Nichts kann Lichtjahre "dauern".

Donidoni2 schrieb:Man sollte hier immer klar ausdrücken meint man die Wahrscheinlichkeit für leben im Universum oder leben nicht auf der Erde im Universum.

Ja, das ist ein weiteres Problem. Jedoch, und deswegen kommen viele ja auch gerne mit der Voraussetzung eines unendlich großen Universums: selbst wenn die mittlere Auftretenswahrscheinlichkeit von Leben unter einem Stern 1/n so gering ist, daß n die Zahl sämtlicher Sterne des beobachtbaren Universums übersteigt, liefe die Zahl belebter Welten im unendlichen Universum dennoch auf unendlich hinaus.

Was anderes aber ist die grundsätzliche Möglichkeit, daß es selbst in einem unendlich großen Universum Objektkategorien gibt, die nur in endlicher Anzahl vorkommen. Rein rechnerisch muß man bei solchen Phänomenen dann sagen, daß deren Wahrscheinlichkeit eben n/[unendlich] ist, wobei n endlich ist, und also nicht >0 sein kann.

Der Witz ist, daß viele die "Wahrscheinlichkeit = 0" für gleichbedeutend mit "ausgeschlossen", "unmöglich" odgl. halten in dem Sinne, daß was in nem unendlich großen Universum die Wahrscheinlichkeit Null besitzt, das wird von den Eigenschaften, Naturgesetzen etc. des Universums nicht zugelassen. Daß etwas möglich ist, sich aber dennoch selbst in einem unendlichen Universum nicht oder nur endlich oft ereignet, liegt für viele außerhalb des Denkens.

Dazu komme ich auf das Problem des Infinite-Monkey-Theorems. Wenn ich unzählige Affen wahllos auf Schreibmaschinen (oder PC-Tastaturen) klimpern lasse, müßte doch eigentlich, wenn die nur lang genug Zeit haben, irgendwann einmal Shakespeares Gesamtwerk ohne Fehler aufs Papier gebracht werden. Rein mathematisch betrachtet ist das korrekt. Wenn auch die Affenzahl und die Zeiträume unvorstellbar riesig sind, um auch nur einen einzigen Satz herauszubekommen. (Wer es nicht kennt, einfach mal Wikipedia: Infinite-Monkey-Theorem lesen).

Funktioniert nur nicht. Man stelle sich mal sich selber vor, wie man wahllos mit den Fingern auf ner Tastatur rumklimpert. Einfach mal in der Luft "klimpern" und dabei den Händen zuschauen. Eins drei fix haben sich da nämlich Routinen eingestellt. Bei mir etwa gehen die Finger vom kleinen Finger bis zum Zeigefinger hintereinander nach unten, und dann wieder beim kleinen Finger beginnend, immer fort. Und das bei beiden Händen gleichzeitig, also beidseitig von außen nach innen geklimpert. Somit kommen ziemlich gleichmäßig oft Buchstaben beider Tastaturseiten aufs Papier, und zwar erst welche vom Rand, dann näher zur Mitte, dann aus der Mitte, und wieder vom Rand her. Buchstabenfolgen mit Schwerpunkt auf einer Tastaturseite bzw. mit einer Reihung von der Tastaturmitte zum Rand sind zumindest massiv unterrepräsentiert. So kriegt man keinen ganzen Text zusammen.

Oder das Tippen nur mit den beiden Zeigefingern. Kann man auch ausprobieren. Auch da stellt sich irgendwann ne Routine ein. Erst mal die, daß ich wieder abwechselnd mit dem linken, dann dem rechten Zeigefinger tippe. Dabei laß ich meine Hände über der Tastatur kreisen, beide in Uhrzeigersinn oder beide gegenläufig o.ä., gleichzeitig oder um einen halben Kreis versetzt. Auch so erhalte ich eine bestimmte Buchstabenverteilung, vorgegeben durch Handbewegungsroutine und Tastaturbelegung. Einen ganzen Text erhalte ich so nicht.

Ist mit Affen nicht anders. Sollten die dahingehend dressiert werden, auf der Tastatur zu klimpern, wird auch bei denen die Handanatomie zu Fingerbewegungs- und Handkreisel-Routinen führen.

Und was ist mit Affen, die nicht dressiert werden, sondern einfach aus Neugier mal auf Tasten tippen, später halt mal aus Versehen über die Tastatur latschen und dabei wahllose Buchstabenfolgen erzeugen? Stellen sich auch da Routinen ein?

Ja!

Es war eines der skurrilsten Forschungsexperimente der Mathematikgeschichte: 2002 spendierten Forschende der University of Plymouth sechs Schopfmakaken eines Zoos im englischen Devon eine Schreibmaschine. Vom 1. Mai bis zum 22. Juni durften sich die Tiere darauf austoben – die getippten Buchstaben wurden über ein elektrisches Signal an die Fachleute übertragen und gespeichert. Ihr Ziel war es, das »Infinite-Monkey-Theorem« zu testen.

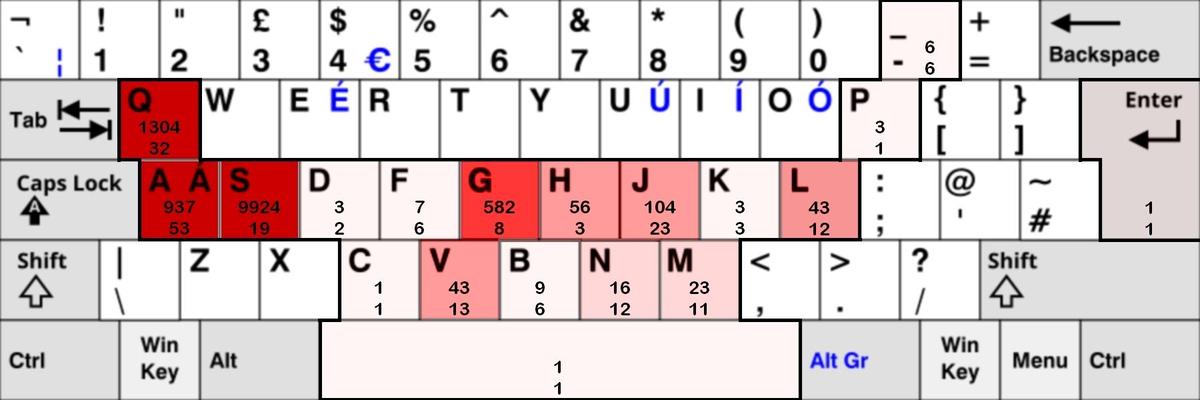
Quelle: https://www.spektrum.de/kolumne/infinite-monkey-theorem-mit-genuegend-zeit-ist-alles-moeglich/2211128
https://web.archive.org/web/20090318143423/http://www.vivaria.net/experiments/notes/publication/NOTES_EN.pdf

Hier mal die Zahl der von den Makaken produzierten Buchstaben (oben) sowie die Zahl der Blöcke (unten), in denen hintereinander stets der selbe Buchstabe erzeugt wurde.

Original anzeigen (0,2 MB)

Von der gesamten Tastatur wurde nur ein mondsichelförmiger Bereich angeschlagen, einzig die Zeilenumbruchs-Taste außerhalb davon wurde ein mal getätigt. Alle anderen benutzten Tasten liegen direkt zusammen, es gibt keine Taste dazwischen, die nicht angeschlagen wurde. Wie auch immer dies zustande gekommen ist, hier hat sich eine Routine eingestellt, die zu einer abgrenzbaren Verteilung geführt hat. Weitere Routinen zeigen sich in der Häufigkeit des Anschlags. Besonders sticht die massive Häufigkeit der Anschläge ganz links hervor: Q, A und S. Auch vom V übers G bis zum J gibt es eine deutliche Häufung, nur das L liegt ein wenig von diesem "Mittelfeld" entfernt. Die am seltensten angeschlagenen Tasten liegen im Randbereich des "Mittelfelds" bzw. zwischen diesem und dem "Spitzenfeld".

Insgesamt wurden 13066 Zeichen erzeugt (der eine Zeilenwechsel mitgezählt), davon mit 9924 mal das S fallen knapp 76 Prozent auf einen einzigen Buchstaben. Von 26 möglichen Buchstaben sind zehn Buchstaben gleich überhaupt nicht verwendet worden, das sind knapp 38,5 Prozent des Alphabets. Ferner findet sich das S auch nicht querbeet verteilt, sondern in relativ wenig (19) Blöcken. In einem Block stehen 7241 S direkt hintereinander, fast 55,5 % des gesamten "Textes"!

Nehmen wir mal an (was wahrscheinlich ist), daß die allermeisten Folgen gleicher Buchstaben hintereinander durch ein Dauerdrücken der entsprechenden Buchstabentaste erzeugt wurden, und zählen jeden Block gleicher Zeichen stets nur als ein angeschlagenes Zeichen, dann wäre der erzeugte Text nur 212 Zeichen lang. In dem Falle aber bestünde der Text über eine Länge von sechzig Zeichen nur aus ständig wechselnden je 30 Q und A (Block 18-77 von 212). Q und A liegen übrigens direkt nebeneinander.

Es treten also auch ohne Klimperroutine gewisse Regelmäßigkeiten / Routinen auf, welche definitiv einen sinnigen Text echter Sprache verhindern. Und genau solche "Routinen", bedingt durch z.B. anatomische wie feinmotorische Bedingungen zum einen sowie der Tastenanordnung zum anderen, lassen kein Shakespeare-Werk entstehen. Hier ergibt sich die Bestimmung des Wahrscheinlichkeitswertes eben nicht aus der rein "mathematischen" Betrachtung, wie wahrscheinlich eine wie lange Folge von welchen Buchstaben ist

Unterm Strich ist die Wahrscheinlichkeit, daß so das Shakespeare-Gesamtwerk entsteht, trotz aller "numerischer Machbarkeit" und frei von jeglicher Naturgesetz-Verletzung dennoch Null. Sollten unendlich viele Affen unendlich lange tippen, und sollte doch mal so ein Gesamtwerk herauskommen, dann ist dennoch keine Wiederholung gewährleistet.

Noumenon schrieb:Da verwechselst du relative Häufigkeit mit Wahrscheinlichkeit. Wenn du 3x Lotto spielst und 1x gewinnst, liegt die relative Häufigkeit des Gewinns bei 1/3, aber daraus folgt nicht, dass auch die Wahrscheinlichkeit bei 1/3 liegt.

Definitiv nö. Drei mal Lottospielen ist was Anekdotisches. Selbst ein ganzes Menschenleben voller Lottospiele ist anekdotisch, und die Häufigkeit der Gewinne dabei ist noch lange keine Wahrscheinlichkeit, da gebe ich Dir recht. Aber ich sprech ja überhaupt nicht von einer begrenzten Auswahl an Events, bei denen ich die Häufigkeit eines bestimmten eingetroffenen Ereignisses auszähle und dann als X/n zur Wahrscheinlichkeit erkläre. Wir sprechen hier nun mal die ganze Zeit vom ---> unendlichen Universum! In Deinem Bild müßtest Du schon sämtliche Lottospiele der Welt von Anbeginn an nehmen - und selbst das wäre zu wenig, weil es weitere Spiele geben wird. Du müßtest schon von "absolut allen" Lottospielen sprechen. Und sogar das ist nicht adäquat, weil es eben endlich viele sein werden, das "Anekdotische" also nie ganz verschwunden sein wird.

Beim "ein ganzes Leben lang Lotto spielen" immerhin schwindet das Anekdotische schon deutlich, jedenfalls partiell. Wenn Du in dem Falle die Zahlen der geknackten Jackpots, Sechser und Fünfer aufschreibst und je ein /n dranfügst (n für die Gesamtlottospielzahl dieses einen Lebens), bliebe es deutlich anekdotisch und nicht dem Wahrscheinlichkeitswert entsprechend. Machst Du das hingegen mit den gewonnenen Dreiern (gar noch mit den gewinnlosen Zweiern und Einern), dürfte sich der so ermittelte Wert X/n schon verdammt nah am betreffenden Wahrscheinlichkeitswert befinden. Die, nun ja, Wahrscheinlichkeit ist verdammt groß, mit diesem "Auszählen" an den tatsächlichen Wahrscheinlichkeitswert zu kommen. Je größer das n der Auszählung gegenüber dem n des Wahrscheinlichkeitswertes ist, desto größer fällt die Näherung der Auszählung an den Wahrscheinlichkeitswert aus.

Und wie gesagt, wir sprechen hier nun mal die ganze Zeit vom ---> unendlichen Universum! Und da sprichst Du vom Auszählen anekdotischer dreier Lottospiele??? Weia!

Noumenon schrieb:Wie gesagt: Die Wahrscheinlichkeit definiert sich nicht durch einfache Division auf Basis einer Milchmädchenrechnung (dein "n/X").

Ja klar. Hübsch behauptet, aber Null Aufweis (Deine unpassenden 3 Lottoscheine mal außen vor gelassen).

Noumenon schrieb:Nehmen wir als Beispiel die natürlichen Zahlen, ziehen eine x-beliebige Zahl und fragen uns, wie hoch die Wahrscheinlichkeit gewesen ist, diese konkrete Zahl (bspw. 42) gezogen zu haben. Jetzt sagst du: Null! Deine Begründung: 1/Unendlich = 0, ein einzelnes Ergebnis geteilt durch unendlich viele Möglichkeiten ergäbe eben Null (deine Milchmädchenrechnung). So weit, so gut. Wäre aber für alle möglichen Zahlen die Wahrscheinlichkeit exakt 0, diese Zahl zu ziehen, würden sich alle Wahrscheinlichkeiten zu 0 aufsummieren, im Widerspruch zu Forderung, dass sich alle Wahrscheinlichkeiten zu 1 aufsummieren müssen. Und damit ist eben ausgeschlossen, dass p für alle Zahlen exakt 0 ist.

Und begreift es fortgesetzt nicht. Ja scheiß drauf, daß die Mathematik daran scheitert, dieses Dilemma aufzulösen. Aber sie immerhin "weiß" es besser als Du!
Nimm eine Strecke, miß ihre Länge. Sicher ein Wert >0, gell?
Woraus besteht diese Linie? Aus Punkten.
Gibt es Zwischenräume ohne Punkte? Nein.
Welche Ausdehnung hat ein Punkt? Null.
Auf welchen Wert summieren sich alle diese Nullen? Auf das anfängliche >0 jener Strecke.

Klar, da hab ich wieder mit Überabzählbarkeiten gehändelt wie weiland mit dem Beispiel der Reellen Zahlen. Falls Du das einwenden willst, kannste gerne erst einmal erklären, wieso das Addieren von Nullen überabzählbar >0 ergibt, wohingegen Deine obige Erklärung genau dieses nun mal ausschließt, daß das Aufsummieren von Nullen was anderes als Null ergeben könnte. Anschließend darfste auch erklären, wieso abzählbare Unendlichkeiten anders als die Nichtabzählbarkeiten dennoch bei Null blieben.

Wenn Dir letzteres gelungen sein sollte, werd ich Dir mit nem Dreieck und ner abzählbaren Unendlichkeit (natürliche Zahlen) das Gegenteil beweisen.

Aber hübsch der Reihe nach. Erst mal Du.

Noumenon schrieb:perttivalkonen schrieb:
War ja auch meine Folgerung, daß diese Umkehr aufs selbe hinausläuft, was Du gesagt hast. Daß Du auch noch auf eine Verschiedenheit zwischen stetiger und diskreter Warhscheinlichkeit verweist, ist dabei geschenkt, solange Du Null Aufweis erbringst, daß dieser Unterschied für das hiesige Problem relevant ist (is ja nich so, als ob da alles verschieden wäre, etwa das Problem von [endlicher Wert] / [unendlicher Wert] worauf ich mich ja bezogen hatte.

Ja, der Unterschied ist schon relevant, schließlich sind Planeten abzählbar.

Echt jetzt? Du erklärst, daß ein Unterschied zwischen X und Y relevant sei, und weist dies nach, indem Du auf den bloßen Unterschied hinweist???

Noumenon schrieb:perttivalkonen schrieb:
Zeig doch mal bitte, daß es falsch ist, daß der Wert 1/n sich bei ständiger Erhöhung von n der Null nähert, wie sich n dem Unendlich nähert. Anders ausgedrückt: sobald jemand daherkommt und n direktemang auf [unendlich] setzt (Universum unendlich), der Wert 1/n genauso direktemang bei 0 landet.

Nein, das ist so schon richtig, wurde aber auch nicht bestritten.

Zu Deutsch, Dein

Noumenon schrieb:ex falso quotlibet

trifft also gar nicht zu. Danke, meine Rede!

Noumenon schrieb:Ich habe die Diskussion zwar nicht mitverfolgt

Ja, den Verdacht hatte ich auch schon.

Noumenon schrieb:Und wir wissen nun einmal, dass Leben endstanden ist, damit kann die Wahrscheinlichkeit eben nicht bei Null liegen

Und das ist ne Behauptung ohne Herleitung - für das unendliche Universum wohlgemerkt. Bei endlichen Mengen isses was anderes, da reicht der Aufweis (Dividend ist >0) schon aus. Nur eben nicht bei Unendlichkeiten.

Und komm nicht wieder mit Milchmädchen und Häufigkeit statt Wahrscheinlichkeit. Denn was machst Du an dieser Stelle? Dein "mindestens uns gibts ja" beruft sich nicht auf den Wahrscheinlichkeitswert von Leben, sondern hantiert ebenfalls mit "Häufigkeit".

Noumenon schrieb:Da hier insbesondere auf der letzten bzw. mittlerweile vorletzten Seite (1.111) wild über Unendlichkeiten sinniert wurde, ohne zu einem vernünftigen Ergebnis zu kommen, macht eine Klarstellung schon Sinn.

Würde, da geb ich Dir recht. Aber ich sagte ja sinngemäß "wenn von Dir da nix zu kommt (und Du nur den bisherigen haltlosen Kram wiederholst), dann klemms Dir".

continuum schrieb:Ja, das habe ich mir auch schon gedacht, aber dann müsste es schon fast ein Raumschiff der Grösse eines Planeten sein im Sinne einer Wirtschaft, siehe das von Perttivalkonen (O'Neil Zylinder, oder ähnliches), damit man das überbrücken könnte so von der Aussage von @gagitsch mit den ca. 700.000 Jahre, auch wenn wir mal 10x schneller fliegen könnten, dann ist es immer noch schnurrgerade 70.000 Jahre, einfach unheimlich.

Die Entfernungen sind unheimlich, ja.

Es gibt ja Forschungen die die Reise deutlich schneller macht.

Ob die rd 20 Jahre die Noumenon genannt hat, realistisch sind, kann ich nicht abschätzen, das was ich so las, war bei ca 800-1000 Jahre gelandet wenn Versuchsantriebe Serienreife erhalten.

continuum schrieb:Das andere ist, dass wir zurzeit und wahrscheinlich auch in den nächsten 20 Jahren nicht in der Lage sein werden, unsere Antriebe für bemannte Flüge auf etwa 10% der Lichtgeschwindigkeit zu bringen, aber man weiß ja nie.

Mit ner sonde ist das dann wohl das eine, mit Menschen was anderes.

Noumenon schrieb:Wenn du 3x Lotto spielst und 1x gewinnst, liegt die relative Häufigkeit des Gewinns bei 1/3, aber daraus folgt nicht, dass auch die Wahrscheinlichkeit bei 1/3 liegt.

Ich habe nicht alles verfolgt aber die Aussage stimmt so ob „anekdotisch“ oder nicht.

Die beobachtete relative Häufigkeit zu gewinnen ist 1/3 auch wenn die tatsächliche Wahrscheinlichkeit mikroskopisch klein ist.

Noumenon schrieb:Wenn Vergleiche hinken, ist ja schon schlimm, aber wenn sie förmlich auf dem Bauch kriechen...? Dein Beispiel ist deterministisch, konstruiert, welches eine Ausnahme künstlich erzwingt, indem es explizit vorgibt, wo genau "101" vorkommen darf. Ein Universum mit zufälligen, aber wiederholbaren physikalischen Prozessen funktioniert probabilistisch: Wenn es in einem Teil des Universums Bedingungen gibt, die zur Entstehung von Leben (oder anderer Naturphänomenen) führen, gibt es keinen Grund, warum diese Bedingungen nicht auch an anderer Stelle reproduzierbar sein und in einem unendlich großen Universum sogar unendlich oft vorkommen sollten. Alle Gegen"argumente" sind konstruiert a la "Die Zahl 42 gibt's ja trotz unendlich vieler Zahlen auch nur ein einziges Mal!"

Man merkt, dass du zwar sehr belesen bist aber deine mathematische Denkweise kommt mir doch sehr abgelesen und beschränkt vor. Dir fehlt leider komplett die Fähigkeit gedanklich etwas zu übertragen.
Es geht hier um ein Beispiel, dass eine bestimmte Struktur als Binärcode dargestellt auch in der Unendlichkeit nicht wiederholt werden muss.
Natürlich sind Beispiele konstruiert.

Du solltest vielleicht mal einen Gang runterschalten und nicht immer deinen ganzen Fokus darauf legen etwas zwanghaft zu widerlegen. (Auch wenn du oft bestimmt recht hast)

Und das deine Umgangsformen allgemein sehr fragwürdig sind weißt du bestimmt selber.

Ich bin mir zwar sicher, dass du in irgendeiner Form mathematisch etwas gelernt hast aber sehr wahrscheinlich nicht Physik oder Mathematik auf Master/Diplom. Eher Informatik, oder Lehramt. Wobei Lehrer glaube ich nicht so gut wäre.

Donidoni2 schrieb:Ich bin mir zwar sicher, dass du in irgendeiner Form mathematisch etwas gelernt hast aber sehr wahrscheinlich nicht Physik oder Mathematik auf Master/Diplom. Eher Informatik, oder Lehramt. Wobei Lehrer glaube ich nicht so gut wäre.

Ich tippe auf Schwerpunkt Philosophie :popcorn: Wobei der Personenbezug ja eigentlich rauszuhalten ist.
Jedenfalls kam mir seine Argumentation auch unzutreffend vor; in einigen Punkten sogar offensichtlich eklatant. Ich habe nur bei diesem Thema nicht das Rüstzeug an Bord, um schnell mal die wirklich zutreffenden Gegenargumente hinzulegen, die dann auch in der Tiefe standhalten. Daher der eine oder andere Abbruch beim Posten von Beiträgen hier. :lolcry:

Donidoni2 schrieb:Du solltest vielleicht mal einen Gang runterschalten und nicht immer deinen ganzen Fokus darauf legen etwas zwanghaft zu widerlegen.

Diese Diskussion hier geht bereits sehr viel länger als du hier angemeldet bist und die Einwände bzw. die Sichtweise von @Noumenon sind durchaus berechtigt und schon in vielen Varianten oftmals vorgetragen und nun von @Noumenon auf den letzten Seiten sehr gut zusammenfassend argumentiert.

Ob sie letztlich stimmig und korrekt begründet sind, wird vielleicht seine Diskussion mit Valkonen zeigen, aber ich befürchte Letztgenannter wird wieder einmal maulig aus der Diskussion aussteigen.

Donidoni2 schrieb:Und das deine Umgangsformen allgemein sehr fragwürdig sind weißt du bestimmt selber.

Schlechte Umgangsformen kann man @Noumenon nun wirklich nicht vorwerfen. Im Gegenteil - und ich empfinde eigentlich deine merkwürdige "Analyse" seines beruflichen bzw. akademischen Werdeganges doch als sehr despektierlich und als völlig unangebracht.


Also schalte du mal bisschen runter, Neuling! :Y:

Nemon schrieb:Jedenfalls kam mir seine Argumentation auch unzutreffend vor; in einigen Punkten sogar offensichtlich eklatan

Weil?

Nemon schrieb:Ich habe nur bei diesem Thema nicht das Rüstzeug an Bord, um schnell mal die wirklich zutreffenden Gegenargumente hinzulegen, die dann auch in der Tiefe standhalten

Achso, aber Hauptsache deinen Senf dazu geben. Wer braucht denn schon Inhalte?! :)

@RogerHouston
Ja nu. Es geht sicher nicht nur mir so. Darf man ja mal gesagt haben. Man muss sich bei der Vielfalt an Themen, in denen man mitunter involviert ist, hier auch manchmal entscheiden, worauf man sich noch einlassen kann aus Gründen der zeitlichen und gedanklichen Kapazitäten. Ab und zu einen wackeligen Einwurf von der Seitenlinie wird man sich doch genehmigen dürfen.

RogerHouston schrieb:Weil?

Die eine Sache ist das digitale Verständnis der "0" vs. infinitisemal, Beispiel hier:

Noumenon schrieb am 18.02.2025:Eine Wahrscheinlichkeit von exakt Null für die Entstehung von Leben im Falle eines unendlich großen Universums wäre nur dann zutreffend, wenn Leben grundsätzlich unmöglich wäre.

Diese Sache ging mir direkt sehr gegen den Strich:

Noumenon schrieb am 18.02.2025:Doch, wir wissen, dass die Wahrscheinlichkeit für die Entstehung von Leben größer Null ist, denn mindestens hier auf unserer Erde ist Leben entstanden. Damit folgt direkt, dass in einem unendlich großen Universum auch die Anzahl belebter Planeten gegen unendlich geht.

Nemon schrieb:Diese Sache ging mir direkt sehr gegen den Strich:

Nemon schrieb:Noumenon schrieb am 18.02.2025:
Doch, wir wissen, dass die Wahrscheinlichkeit für die Entstehung von Leben größer Null ist, denn mindestens hier auf unserer Erde ist Leben entstanden. Damit folgt direkt, dass in einem unendlich großen Universum auch die Anzahl belebter Planeten gegen unendlich geht.

Mir persönlich geht das Konzept der Unendlichkeit gegen den Strich und bin der Auffassung, dass es sowas nicht gibt.

Lässt man sich aber darauf ein, so finde ich es als logisch, dass in einem unendlichen Universum die Kombinations-Möglichkeiten von beispielsweise Atomen dennoch begrenzt, also endlich sind. Wenn Leben nun als eine bestimmte Kombination von Umständen (Atomen in meinem Beispiel) ist, so müsste sich das zwangsläufig wiederholen - und zwar unendlich.
Aber ja, das ist ja zum Einen der Disput hier.

RogerHouston schrieb:Schlechte Umgangsformen kann man @Noumenon nun wirklich nicht vorwerfen. Im Gegenteil - und ich empfinde eigentlich deine merkwürdige "Analyse" seines beruflichen bzw. akademischen Werdeganges doch als sehr despektierlich und als völlig unangebracht.


Also schalte du mal bisschen runter, Neuling! :Y:

Sry.
Aber Ich finde sowohl perti als auch jetzt noumenon könnten das Ganze weniger gereizt angehen. Ich habe den Eindruck da wird etwas gelesen und bevor wirklich darüber nachgedacht wird geht es darum wie man das gesagte schlecht machen kann. Und dann frage ich mich auch warum nicht einfach geschrieben wird: das ist falsch das ist so und so. Wenn möglich werden unterschwellige Beleidigungen eingebaut.

RogerHouston schrieb:Wenn Leben nun als eine bestimmte Kombination von Umständen (Atomen in meinem Beispiel) ist, so müsste sich das zwangsläufig wiederholen - und zwar unendlich.
Aber ja, das ist ja zum Einen der Disput hier.

Bei müsste, da bin ich nicht sicher
Bei sollte, da wäre ich bei dir.

Ein Würfel mit 6 zahlen drauf, unendliche möglichkeit, wird es alle Zahlen jemals gewürfelt? Müsste.....
Sollte......

Was spräche dagegen, so wie du ja gesagt hast, wenn die Zahlen begrenzt sind (aber die versuche unendlich), das dann ja eigentlich aus der Logik passieren müsste.

Weiss nicht mehr wer das gesagt hat mit, dann müsste auch der zufall sein, wenn ein affe, unendlich viel mal auf eine tastatur klimbert, dass der irgendwann das Buch Harry Potter schreibt und die fortsetzung.

Und jetzt bin ich unsicher mit "müsste".....

Sollte doch, aber genau hier hört es dann für mich auf, eher weil mein Hirn an der Grenze ist. ;)

continuum schrieb:Weiss nicht mehr wer das gesagt hat mit, dann müsste auch der zufall sein, wenn ein affe, unendlich viel mal auf eine tastatur klimbert, dass der irgendwann das Buch Harry Potter schreibt und die fortsetzung.

Du kannst die Wahrscheinlichkeit dafür ja ausrechnen und wenn du n mal tippen lässt geht der Grenzwert für die Wahrscheinlichkeit lim n -> unendlich auch gegen 1. aber das ist eben nur die grenzwertbetrachtung. Solange du an einer bestimmten Zeit aufhörst zu tippen ist die tatsächliche Wahrscheinlichkeit immer kleiner 1.

Da macht es auch keinen Unterschied ob Münzwurf oder ein ganzes Harry Potter Schreiben.

@Donidoni2
Sehr gut, dann kannst du mir die Lotto Zahlen ausrechnen? Aber bitte per PN, nicht das ich noch teilen muss..... ;)