Leben im Sonnensystem durch Panspermie möglich?

perttivalkonen schrieb:zwar ging es in der Testreihe darum, wie viel überleben kann, doch nur im Sinne einer Relation zum Beschleunigungsdruck. Letztlich gings um die Frage, ob was überleben kann. Und mittlerweile bezweifle ich wie gesagt, daß diese Art Experiment / Testreihe da wirklich verwertbare Antworten liefert.

Ja, und ich habe dazu angemerkt, das es unter günstigen Umständen relativ egal ist, wieviele Mikroben tatsächlich überleben, sofern ihre Zahl zur Vermehrung ausreicht. Wie gut die Testreihen da die realen Bedingungen widergeben kann ich nicht beurteilen...

wolf359 schrieb:Ja, und ich habe dazu angemerkt, das es unter günstigen Umständen relativ egal ist, wieviele Mikroben tatsächlich überleben, sofern ihre Zahl zur Vermehrung ausreicht.

Was sollen das denn für günstige Bedingungen sein, daß die Bakterienzahl dafür ausreichend wäre? Ne Bakteriendichte wie in Lebewesen oder in Mutterboden, gerne auch ne Endolithendichte direkt an ner Steinoberfläche kommt jedenfalls nicht in Frage. Auf der anderen Seite findet während eines Transspermie-Ereignisses eine Dezimierung nicht nur einmal statt, sondern gleich mehrmals nacheinander; ich verwies ja darauf.
Impaktdruck/Beschleunigungsdruck -> physische Dezimierung
druckbedingte Erwärmung -> chemische Dezimierung
Abkühlung im All -> Dezimierung
kosmische Strahlung -> Dezimierung
Länge des Cryoschlafs -> Dezimierung
Impaktdruck/"Brems"druck -> Dezimierung
druckbedingte Erwärmung -> Dezimierung

Berechnet wurde aber nur ein einziger Dezimierungsaspekt, nämlich die erste Dezimierung durch den reinen Druck (wobei der zweite Aspekt mit hineinspielt, aber womöglich wegen der Projektilgröße um Größenordnungen weniger von Belang ist).

Ob die Dauer der Beschleunigung eines Projektils auf fünfkommanochwas km/s "sehr kurz" tatsächlich der kurzen Beschleunigungsdauer eines Impaktgeschehens entspricht, geht aus dem Paper nicht hervor, ich wage es zu bezweifeln. Vor allem aber entsprechen die fünfkommanochwas nicht den Elfkommanochwas der irdischen Fluchtgeschwindigkeit, was die Aussterberate nochmals gehörig verschlechtert.

Die dritte Dezimierung, die Abkühlung, könnte eine zu vernachlässigende Größe sein. Die vierte stellt auch nur für kleine Objekte ein Problem dar bzw. bei großen nur für oberflächennahe Lebensformen. Andererseits sorgt ein Impakt eben auch vor allem für kleines Auswurfmaterial.

Eine mittlere Aussterberate von 10^-2 ist jedenfalls total illusorisch. Bei 10-4 im Mittel und ohne die Cryo-Dezimierung würde schon nur noch ein Bakterium von 10²⁴ überleben. Bei 10¹⁴ Mikroben in Mutterboden müßten schon 10.000 Tonnen Mutterboden nach einem Impakt auf nem anderen Himmelskörper landen. Entsprechend sehr viel mehr müßte ins All geschleudert werden, da das so ins All gelangte Material a) auch auf den Heimathimmelskörper zurückfallen kann, egal wann, b) auf nem Himmelskörper mit Atmosphäre auch komplett verglühen kann, c) bis Sankt Nimmerlein im All verbleiben kann... Wenns nun aber gar nicht mikrobenreicher Mutterboden ist, der es ins All schafft, sondern um Größenordnungen weniger bewohntes Gestein, dann müssen wir wohl eher fragen, wie viele Milliarden genügend großer Impakte wir benötigen, damit auch nur ein einziges Bakterium mal lebend irgendwo ankommt.

perttivalkonen schrieb:Nee Du, Bodenbakterien kannste knicken.

Gut, überredet, klammern wir Bodenorganismen mal aus.

perttivalkonen schrieb:Nee Du, wenn etwas überleben kann, dann nix in "Mikrometeoriten", sondern in kompaktem Gestein genügender Größe.

Schon klar, je größer der Brocken, desto besser.

perttivalkonen schrieb:Allerdings ist die Endolith-Dichte in Gestein nicht sonderlich hoch.

Naja, also 10⁶/g bis 10⁸/g sind selbst in tieferen Gesteinsschichten nicht unüblich und immer noch recht beachtlich. In einer Gesteinsprobe vom Gewicht einer Tafel Schokolade können sich also locker mal 'ne Milliarde Bakterien tummeln.

perttivalkonen schrieb am 28.10.2019:Immerhin scheinen uns Marsmeteoriten von acht Impaktereignissen der letzten 20 Millionen Jahre erreicht zu haben, was pro Milliarde Jahren hochgerechnet 400 Events bedeutet, bei denen lebenshaltiges Gestein ins All geschleudert werden kann. In 3 1/2 Milliarden Jahren kämen da 1400 Events zusammen, bei denen Transspermie hätte passieren können. Und pro Event werden zahlreiche Klumpen ins All geschleudert, und die beglücken womöglich nicht nur einen weiteren Himmelskörper mit nur je einem Meteoriten.

Ich weiß zwar nicht, woher genau die Angaben stammen, aber wenn bei mehr als 1000 Events etliche Mega- und mitunter vielleicht sogar Gigatonnen (?) kontaminiertes Material ins All geschleudert werden, wäre das doch eigentlich schon recht ordentlich.
Wenn ich richtig informiert bin, wurden auf der Erde bisher um die 30 Einschlagkrater mit einem Durchmesser von 30km oder mehr nachgewiesen (die Dunkelziffer dürfte freilich höher sein). Was da für Brocken mit Milliarden Tonnen an Gewicht auf die Erde geknallt sind, kann man leicht nachrechnen. Und da hopsen dann nicht mal eben nur drei Kieselsteinchen kurz hoch in die Luft, sondern werden "Unmengen" (Kilo-, Mega-, Gigatonnen?) an Material aus den oberen Gesteinsschichten gerissen und ins All befördert. Und wenn man auch kleinere Impacts mitzählt, kommt man wohl auf deine 1400 Events, insofern würde ich deine Zahl jetzt erst einmal so hinnehmen, solange ich keine besseren habe. :)

Mars und Erde sind nicht direkt vergleichbar (Fluchtgeschwindigkeit, Oberflächenbeschaffenheit, Atmosphäre...) und beim Mars genügen sogar schon kleinere Treffer, um Material aus dem Planeten zu reißen:

"Marsmeteoriten entstehen mehrheitlich nicht durch größere Asteroideneinschläge auf dem Mars, sondern bereits durch Einschläge, die Krater von 3 km Durchmesser hinterlassen. Durch die Wucht des Einschlags wird entsprechend der Kratertiefe Marsgestein verschiedenen Alters ins All geschleudert. Einige dieser so freigesetzten Gesteinsbrocken erreichen als Meteoriten die Erde. Unter diesen war aufgefallen, dass sie im Mittel sehr viel jünger waren, als sich dies durch äußerst seltene Asteroideneinschläge erklären ließe. Kleinere Einschläge schleudern jüngere Gesteinsschichten aus geringeren Tiefen ins All und sind häufiger."
Wikipedia: Marsmeteorit#Herkunft

An Material mangelt es insofern nicht, da fliegt genug durch die "Luft". Die Frage ist halt nur, unter welchen Bedingungen. Wobei hier ja scheinbar schon festgestellt wurde, dass man den ganzen Trip grob in drei Phasen unterteilen kann: Auswurf, Transit, Eintritt. Im Detail wird's aber spätestens dann kompliziert, wenn es diverse Himmelskörper im Sonnensystem, alle möglichen Zeiträume (vom Hadaikum zur Gegenwart) und Bedingungen usw. zu berücksichtigen gilt.

perttivalkonen schrieb:Aber was wir schon wissen, schiebt die Chancen für Transspermie doch arg in den Keller.

Eher im Gegenteil. Vor wenigen Jahrzehnten war diese Hypothese noch völlig undenkbar und ein Produkt blühender Fantasie, mittlerweile wird sie ernsthaft in Betracht gezogen und ist längst zum Gegenstand etlicher wissenschaftlicher Paper geworden.

Nicht dass mich dein Standpunkt sonderlich überraschen würde. Vor ca. 100 Jahren wunderte man sich bspw. auch darüber, dass aus Ölfeldern gewonnenes Wasser Schwefelwasserstoff und Hydrogencarbonate enthielt (E. Bastin/F. Greer). Das Problem: Man wusste zwar, dass diese Chemikalien normalerweise von Bakterien erzeugt werden, während man aber gleichzeitig auch wusste (man möchte lieber sagen: zu wissen glaubte), dass Hitze und Druck in jener Tiefe, aus der das Wasser stammte, viel zu groß seien, um dort Leben zu ermöglichen. Und so nahm man noch weitere 50 Jahre lang an, dass die entnommenen Proben schlichtweg mit Mikroben von der Erdoberfläche verunreinigt gewesen sein müssen, denn was man damals wusste (bzw. zu wissen glaubte), schob die Chancen für Leben unter solchen extremen Bedingungen eben arg in den Keller...

perttivalkonen schrieb:Nee Du, Bodenbakterien kannste knicken. Wenn da etwas auf die Reise geht, dann Endolithe, also in festem Gestein lebende Bakterien. Deswegen verwendete man beim STONE-6-Experiment auch Chroococcidiopsis, ein Cyanobakterium, welches u.a. hitze- und strahlungsresistent ist, vor allem aber auch endolithisch lebt.

Ja, sicherlich nicht die schlechteste Wahl angesichts der genannten Resistenzen. Laut diesem 2007 veröffentlichtenPaper scheinen sie allerdings etwas empfindlich auf Druck zu reagieren:

"The vegetative Chroococcidiopsis cells did not survive shock pressures >10 GPa (Fig. 2) where survival rates were reduced to less than 10^(−3). At shock pressures higher than 10 GPa, no survivors were found with a detectable threshold of 10^(−6)."

Man beachte allerdings die lausige Messgenauigkeit (detectable threshold). Und für eine Reise von Mars zur Erde könnte es laut den Autoren auch dennoch reichen, nur halt nicht umgekehrt.

perttivalkonen schrieb:Vor allem aber landet dieses Gestein am Ende nicht in einem Gelatineblock zum schonenden Abbremsen wie in der Testreihe.

Solche groben methodischen Mängel wie der Bakterien-Airbag sind natürlich sehr ärgerlich. Bei obiger Versuchsanordnung hat man die Viecher deshalb einfach mal zwischen zwei Gabbro-Platten eingequetscht, um sie mit Drücken von bis zu 50 GPa und Temperaturspitzen von mehreren hundert °C zu traktieren. Untersucht wurden aber nicht nur Cyanobakterien, sondern auch Sporen (Bacillus subtilis) und Flechten (Xanthoria elegans). Insgesamt kommt die Studie übrigens zu dem Schluss:

"In conclusion, it can be speculated that “lithopanspermia” from Earth to Mars had a high probability during the early history of the Earth; however, during the past 3.8 Ga the probability has been very low."

Vergleichsweise geringe Chancen sehen die Autoren also "nur" für die letzten 3.8 Mrd. Jahre, während sie in der früheren Erdgeschichte (im Hadaikum, da war ja buchstäblich auch "Bombenwetter"...) weitaus größere Chancen für eine Kontamination des Sonnensystems durch terrestrisches Material sehen. Falls das Leben also nicht zu uns gekommen ist, kam es höchstwahrscheinlich von uns:

"Falls das irdische Leben durch chemische Evolution entstand (und nicht entsprechend der Panspermie-Hypothese aus dem Weltall auf die Erde kam), so fand dieser Schritt im Hadaikum statt."
Wikipedia: Hadaikum#Mögliche Entstehung des Lebens

Im Abstract einer 2009 veröffentlichten Studie ("Ancient micronauts: interplanetary transport of microbes by cosmic impacts") sieht man die Dinge scheinbar ähnlich:

"Recent developments in microbiology, geophysics and planetary sciences raise the possibility that the planets in our solar system might not be biologically isolated. Hence, the possibility of lithopanspermia (the interplanetary transport of microbial passengers inside rocks) is presently being re-evaluated, with implications for the origin and evolution of life on Earth and within our solar system. Here, I summarize our current understanding of the physics of impacts, space transport of meteorites, and the potentiality of microorganisms to undergo and survive interplanetary transfer."

Leider ist das Paper kostenpflichtig, hätte natürlich gerne einen Blick reingeworfen. Genauso wie in das folgende, wo man insbesondere auch die Einwirkung mehrerer Faktoren gleichzeitig untersucht hat:

"Bacterial spores are considered good candidates for endolithic life-forms that could survive interplanetary transport by natural impact processes, i.e., lithopanspermia. Organisms within rock can only embark on an interplanetary journey if they survive ejection from the surface of the donor planet and the associated extremes of compressional shock, heating, and acceleration. Previous simulation experiments have measured each of these three stresses more or less in isolation of one another, and results to date indicate that spores of the model organism Bacillus subtilis can survive each stress applied singly. Few simulations, however, have combined all three stresses simultaneously. [...] Spore survival was calculated to be on the order of 10^(−5), which is in agreement with results of previous static compressional shock experiments. These results demonstrate that endolithic spores can survive launch by spallation from a hypervelocity impact, which lends further evidence in favor of lithopanspermia theory."
https://www.liebertpub.com/doi/10.1089/ast.2008.0326

Oder anders ausgedrückt: Was wir schon wissen, schiebt die Chancen für Transspermie doch arg... nach oben.

Auch wenn für knallharte Belege und ein umfassenderes Verständnis natürlich noch einiges an Forschungsarbeit nötig sein wird.

perttivalkonen schrieb:Ob die Dauer der Beschleunigung eines Projektils auf fünfkommanochwas km/s "sehr kurz" tatsächlich der kurzen Beschleunigungsdauer eines Impaktgeschehens entspricht, geht aus dem Paper nicht hervor, ich wage es zu bezweifeln. Vor allem aber entsprechen die fünfkommanochwas nicht den Elfkommanochwas der irdischen Fluchtgeschwindigkeit, was die Aussterberate nochmals gehörig verschlechtert.

Nee, aber die "fünfkommanochwas" entsprechend gerade der Fluchtgeschwindigkeit vom Mars. Auf Merkur, Pluto und diversen Monden liegt sie sogar noch darunter, im Falle des Jupitermonds Europa bspw. sogar "nur" bei ca. 2 km/s, wobei im Falle von Europa aber auch noch hinzukommt, dass seine Oberfläche komplett mit Eis bedeckt ist - zur Erinnerung:

"For the impacts on ice, the survival rate was some 10 times greater than for impacts on agar."
https://academic.oup.com/mnras/article/352/4/1273/1076022

Europa dürfte sich auch eh so einiges an Material einfangen, dadurch dass der fette Jupiter so viel anzieht. Und zwischen Mars und Jupiter fliegt ja auch noch einmal so richtig schön viel Zeug herum und ist im schlimmsten Fall auch noch mit irgendwelchen Viechern kontaminiert. Insofern also auch eine gute Idee, sich die ganze Sache mal etwas näher anzuschauen, allerdings dürften die richtig spannenden Missionen noch etwas auf sich warten lassen (gegen 2030 will man erst einmal klären, ob Europa denn auch wirklich 'nen Ozean unter'm Eispanzer hat)...

Noumenon schrieb:Naja, also 10⁶/g bis 10⁸/g sind selbst in tieferen Gesteinsschichten nicht unüblich und immer noch recht beachtlich. In einer Gesteinsprobe vom Gewicht einer Tafel Schokolade können sich also locker mal 'ne Milliarde Bakterien tummeln.

Das ist gar nichts, wenn von mutmaßlichen 10¹⁰ Mikroben gleich am Anfang eines Transspermie-Ereignis sagenwirmal nur 1 Bakterium von 10⁵ überlebt. Beim Landen sterben dann nochmals alle bis auf eine von 10⁵, und schon hätte gerade mal ein einziger Einzeller von 10¹⁰ überlebt. Nehmen wir doch mal 10²⁰ Mikroben, die auf Reise gehen. Lassen wir davon also erst mal 5 Größenordnungen beim Start wegsterben am Druck der quasi instantanen Beschleunigung auf 11,2+ km/s (nach der Berechnung sollte die Aussterberate sogar noch schröcklicher ausfallen). Und wer nicht vom Druck stirbt, der stirbt am begleitenden Hitzschlag. Macht nochmals, was nehm'wa denn?: sagenwirmal weitere 3 Größenordnungen weniger. Auch das anschließende Einfrieren dürften nicht alle überleben, sind ja keine behutsamen Laborbedingungen, unter denen das erfolgt. Ziehnwa mal 1 Größenordnung ab. Dann fliegt das Geschoß sagenwirmal 20.000 Jahre durchs All, bevor es auf nem Planeten oder Mond aufschlägt. In dieser Zeit sterben zahlreiche Bakterien schlicht deswegen, weil kein Leben für ewig Cryoschlaf ausgelegt ist. Ziehnwa nochmals 4 Größenordnungen ab. Na und dann kommt noch die kosmische Strahlung hinzu, die vor allem das oberflächennahe Leben killt, dank der 20.000 Jahre Dauer aber auch dem tiefer verborgenen Leben an den Kragen geht. Aber ok, ziehnwa nur 1 Größenordnung ab, wir könnens uns ja leisten.

Und nu? Nu gehts ans Landen. Müssen wir da nun nochmals 5 + 3 Größenordnungen runterrechnen? Nein, deutlich mehr, mindestens also 6 + 4, denn die bis jetzt überlebt habenden Mikroben sind ja dennoch von all den Drücken, Hitzen, Strahlen, Kälten und Jahrtausenden betroffen und alles andere als taufrisch und fit wie'n Turnschuh. Wenn ich da jetzt mal die Nullen zusammenzähle, die ich für die ganze Reise von Anfang bis Ende abziehen muß, dann komm ich auf 5+3+1+4+1+6+4. Da komm ich mal eben auf 10²⁴. Hui! Da überlebt von den 10²⁰ vorgeschlagenen Start-Mikroben glatte Null. Hätt ich also 10²⁴ vorschlagen sollen, damit am Ende ein einzelner Einzeller am Leben bleibt. Na ok, bei 10⁸ Mikroben je Gramm Gestein bräuchten wir da schon einen Trumm von 10¹⁶g - sind ja nur läppische 10 Milliarden Tonnen. Das wäre ein mehr als kilometergroßer Gesteinsklumpen. Oder 10 Milliarden tonnenschwere Brocken.

So viele so schwere Brocken müssen erst mal ins All geschleudert werden. Damit ein Bakterium überlebt. Aber nur, wenn gewährleistet ist, daß alle diese 10 Milliarden Trumms auch wirklich mal niedergehen. Und zwar auf nem fremden Himmelskörper, nicht 20.000 Jahre später wieder auf der alten Heimat, wo's ja eh schon Leben gibt. Und dann auch nicht auf Merkur, Mond oder Makemake. Damit da also wirklich ein einzelnes Bakterium landet, sollten wir nochmals (wenigstens) 1 Größenordnung drauf packen. Haben wir also schon 100 Milliarden Geschosse von eine Tonne Lebendgewicht.

Und dann stellt sich natürlich die Frage, ob das Bakterium auf Mars, Europa, Venus oder Enceladus nicht doch noch die Hufe hochreißt, weil ihm die dortigen Bedingungen nicht so recht schmecken.

Wie ich schon schrieb, scheint es in den letzten 20 Millionen Jahren nur 8 Impakten auf dem Mars gelungen zu sein, Material von dort ins All zu schleudern. Auf der Erde mit ihrer höheren Fluchtgeschwindigkeit sollten es weniger Impakte geschafft haben. Wie viele Impakte mit der Fähigkeit, irdisches Material ins All zu schleudern, kann es da in sagenwirmal den letzten 3 1/2 Milliarden Jahren existierenden Lebens auf der Erde gegeben haben? Eindeutig weniger als die für den Mars hochgerechneten 1400 Impakte. Können diese Impakte zusammen bereits so viel Erdmaterial wie hundert Milliarden tonnenschwere Klopse ins All geschickt haben? Wohl gemerkt, so viel Material in größeren Objekten, denn zentimetergroße Bröckchen würden bei Ankunft in ner Atmosphäre oder auf Eis schlicht verglühen, verpuffen, vaporisieren...

Das ist nur ne hypothetische Beispielrechnung. Könnte günstiger sein, aber genauso deutlich ungünstiger.

Noumenon schrieb:wenn bei mehr als 1000 Events etliche Mega- und mitunter vielleicht sogar Gigatonnen (?) kontaminiertes Material ins All geschleudert werden

Ich befürchte, es sind gar nicht so viele.

Wenn ein Impaktor Material aus dem Himmelskörper ins All schleudert, so bildet das allermeiste eine Akkretionsscheibe, von der das meiste wieder auf den Himmelskörper zurück fällt. Ein kleiner Teil davon vermag einen stabilen Orbit einzunehmen. Und sicher vermag auch einiges, die Anziehung komplett zu überwinden und ins All zu entweichen, aber das sollte dann in Relation zum im Orbit verbleibenden Materialanteil stehen.

Und nun schauen wir mal. Damit ein Impaktor so viel Material von der Erde ins All befördert, damit ein ganzer Erdmond voll Masse im Orbit bleibt (7,35 x 10²²kg), sollte der Impaktor schon ungefähr marsgroß sein, also n x 10²³kg Masse besitzen. Nun haben Forscher vor ner Weile die Frage gestellt, ob Phobos und Deimos, deren materiale Beschaffenheit nicht zu eingefangenen Asteroiden passen, womöglich ebenfalls durch einen Impakt entstanden sind. Nach ihren Berechnungen wäre dazu ein Impaktor von 1,25...5 x 10²²kg vonnöten gewesen. Also vielleicht ein Zehntel bis ein Vierzigstel der Masse der hypothetischen marsgroßen Theia. Wenn also ein marsgroßer Impaktor die Masse des Erdmondes von 7,35 x 10²²kg in den Orbit bekommt, aber ein Impaktor mit 2,5...10% dieser Masse nur noch 1,2 x 10¹⁶kg in einen stabilen Orbit bekommt, dann wird ein Impaktor von sagenwirmal Chicxulubasteroiden-Maß wohl kaum sehr viel mehr als ne Megatonne in einen stabilen Orbit oder darüber hinaus bekommen. Wirklich nur grob geschätzt. Vielleicht findest Du ja bessere Angaben.
http://www.planetary.brown.edu/planetary/geo287/PhobosDeimos/papers/Criton2015Icarus-giantimpact.pdf (Archiv-Version vom 25.06.2021)

So, nu isses verdammt spät geworden bei der endlosen Recherche. Nächtle!

@perttivalkonen
Deine (Un-)Wahrscheinlichkeitsrechnerei in allen Ehren, aber es kann ja trotzdem alles etwas anders geschehen sein.
Ich bin zwar auch kein großer Fan von dieser Hypothese, aber einige Faktoren sind ja auch nur Vermutungen.
Der gute alte Zufall darf da doch sicherlich auch noch ein Wörtchen mitreden, oder?
Kann ja sein das zufällig dass es doch geklappt hat in einem speziellen Fall, weil, zufällig doch mehr überlebt haben, weil, zufällig nur kurze Reise und, naja, halt zufällig doch alles begünstigt stattfand.

Will nur sagen, möglich isses doch trotzdem, wenn auch unwahrscheinlich, oder nicht?

@skagerak

Wenn wir bei WünschDirWas wären, würd ich Deine Könntedochsein und Vielleicht und Zufall. Bei der jüngsten Diskussion geht es aber die ganze Zeit über nicht darum, was möglich ist aufgrund unseres Nichtwissens, oder was möglich ist, weil der Zufall jede noch so miese Wahrscheinlichkeit aushebeln kann. Nein, vom Eingangspost an haben alle beteiligten "Seiten" sich auf echte Objekte, echte Mechanismen, echte Beobachtungen berufen und damit argumentiert, und auch eine Entgegnung sollte das Vorgebrachte auf diese Weise zu entkräften suchen. Nicht mit Floskeln, Phrasen und Vielleichts.

Was ich hier vorgerechnet habe, ist eben nicht mit meiner rein hypothetischen Lebensentstehungsrechnerei gleichzusetzen. Hier berufe ich mich auf Bekanntes, Gewußtes. Und zwar weil die anderen es ebenso tun.

Wenn einer sagt, da gibts Aussterberaten von 10^-4...10^-7, dann halte ich dem entgegen, daß das nur für einen Faktor bei einem Transspermie-Event gilt. Wenn jemand auf die Menge von Mikroorganismen in einem Gramm Boden verweist, geh ich da sachbezogen drauf ein. Spricht jemand von Gigatonnen Auswurfmaterial, recherchiere ich und versuche, echte wissenschaftliche Hochrechnungen auszuwerten.

@perttivalkonen
Okay, na dann...
Ich wollte es Dir auch nicht mies reden.

perttivalkonen schrieb:Und wer nicht vom Druck stirbt, der stirbt am begleitenden Hitzschlag.

Die Hitze beschränkt sich nur auf die äußeren Schichten eines Gesteinsklumpen, also die 5cm, von denen du ja bereits gesprochen hattest. 5cm ist faktisch... nichts. Das ist ein kleiner Stein, den man in der Hand halten kann, vergleichsweise ein "Krümel". Bei hinreichender Größe fühlen sich Bakterien im Inneren also pudelwohl, zumal Gestein auch nicht gerade der beste Wärmeleiter ist.

Der Druck (bis zu 50 GPa) breitet sich faktisch durch's gesamte Material aus, für die Temperatur gilt das allerdings nicht, womit das "Hitze-Argument" für Ein- und Austritt entkräftet wäre.

perttivalkonen schrieb:Auch das anschließende Einfrieren dürften nicht alle überleben, sind ja keine behutsamen Laborbedingungen, unter denen das erfolgt.

Auch das hängt von diversen Faktoren ab, so dass man hier keine pauschale Aussage treffen kann. Temperaturausgleich findet bspw. nur über Strahlung und Leitung (im Inneren des Himmelskörpers) statt, nicht aber durch Konvektion, da Vakuum. Hauptsächlich wird Wärme in Form von Strahlung abgegeben, aber eben auch aufgenommen (=> Sonne, Wärmestrahlung).
Die Temperatur des Himmelskörpers hängt vor allem (aber nicht nur) von zwei Faktoren ab: Abstand zur Sonne und Reflexionsvermögen des Himmelskörpers. In einer Entfernung von 1 AE (also Erdnähe) würde die mittlere Temperatur eines Himmelskörpers mit ähnlichem Reflexionsvermögen wie dem der Erde bspw. um die -15 bis -20 Grad Celsius betragen. Die mittlere Temperatur, wohlgemerkt. Inwieweit sich überhaupt ein Equilibrium einstellt bzw. wie sich die Temperatur über den Körper (und dann auch noch als Funktion der Zeit) verteilt, hängt von weiteren Faktoren ab wie etwa die Beschaffenheit (Metall, Stein...) oder die Rotation des Himmelskörpers.
Die Rotation spielt durchaus eine entscheidende Rolle, denn die der Sonne zugewandte Seite ist in jedem Fall wärmer als die der Sonne abgewandete Seite. Und obwohl die mittlere Temperatur eines Himmelskörpers in der Nähe des Mars (ca. 1,5 AE) aufgrund der Entfernung zur Sonne so um die -50°C liegt, kann sie auf Schattenseite bis auf -100°C runtergehen, während sie auf der Sonnenseite angenehme 20°C beträgt. "Dazwischen" herrscht Temperaturverteilung, wo aus Gründen der Stetigkeit faktisch jeder Wert zwischen den Minimum und Maximum angenommen wird. Dreht sich der Himmelskörper schnell genug (quasi wie ein Grillhähnchen über'm Lagerfeuer), verteilt sich die Temperatur mehr oder weniger gleichmäßig über den ganzen Körper (Worst-Case). Im Extremfall hat unser Grillhähnchen aber gar keine Eigenrotation, dann bleibt eine Seite des Grillhähnchens warm, die andere kalt, dazwischen ist die Temperatur über eine Skala zwischen Minimum und Maximum verteilt. Faktisch dürften aber so gut wie alle Asteroiden eine Eigenrotation haben, die zwischen einigen Stunden bis einigen Wochen liegt, was sie in etwa mit Grillhähnchen vergleichbar macht. Nur sind Asteoriden letzten Endes eben doch keine Grillhähnchen. Die Drehachse des Grillhähnchens ist orthogonal zur Hitzequelle, die eines Asteoriden aber nicht unbedingt. Ist der Neigungswinkel klein (die Drehachse zeigt ungefähr in Richtung Sonne), bleibt's dabei: an einem Pol warm, am anderen kalt, dazwischen verteilt es sich.

Das "Kälte-Argument" wäre also ebenfalls entkräftet.

perttivalkonen schrieb:Dann fliegt das Geschoß sagenwirmal 20.000 Jahre durchs All, bevor es auf nem Planeten oder Mond aufschlägt.

Auch wieder nur so'n Durchschnittswert, dazu ein lausiger. Bei einer mittleren Entfernung zwischen Erde & Mars von 225 Mio. km entspräche das im Falle einer direkten Reise (Best-Case-Szenario) einer Geschwindigkeit von über 11000 km pro Jahr, allerdings nur müde 30 km am Tag und 1,3 km pro Stunde - zum Vergleich die Fluchtgeschwindigkeit der Erde: 11,2 km... pro Sekunde. Mag zwar also ein toller Durchschnittswert für's Average-Szenario sein, wie auch immer sich dieser lausige Wert errechnen mag, aber im Durchschnitt war der Teich nur 50 cm tief und trotzdem ist die Kuh ersoffen...

Man kann mindestens davon ausgehen, dass nicht alle Geschosse 20.000 Jahre benötigen, sondern manche mehr und manche eben weniger. Wenn man dazu bedenkt, dass eine direkte Reise zum Mars selbst bei nur 1/10 der Fluchtgeschwindigkeit müde 232 Tage dauern würde, man aber zumindest zur Kenntnis nimmt, dass es natürlich in den seltensten Fällen direkte Hinflüge sein dürften, sondern erst einmal noch ein paar "Tänze" quer durch's Sonnensystem gemacht werden, scheinen mehrere Jahre bis Jahrzehnte dem Average-Szenario schon eher zu entsprechen. Meinetwegen können wir aber auch bei 20.000 Jahren bleiben...

perttivalkonen schrieb:Na und dann kommt noch die kosmische Strahlung hinzu, die vor allem das oberflächennahe Leben killt, dank der 20.000 Jahre Dauer aber auch dem tiefer verborgenen Leben an den Kragen geht. Aber ok, ziehnwa nur 1 Größenordnung ab, wir könnens uns ja leisten.

Auch gegen die kosmische Strahlung bietet eine hinreichend dicke Schicht an Gesteinsmaterial genügend Schutz, wie hier schon festgestellt wurde:

"In ausführlichen Untersuchungen im Weltraum und in unseren Weltraumsimulationsanlagen haben wir gezeigt, daß widerstandsfähige Bakteriensporen bis zu sechs Jahre ungeschädigt im Weltraum überleben können, wenn sie vor der aggressiven Ultraviolett-Strahlung der Sonne geschützt sind. Dies könnte leicht durch eine einige Millimeter dicke Staub- oder Gesteinsschicht geschehen. Um über einen längeren Zeitraum von Tausend oder gar Millionen Jahren vor der kosmischen Strahlung geschützt zu werden, müßte der Gesteinsbrocken allerdings schon erhebliche Ausmaße von etwa zwei bis drei Meter haben."
https://www.dlr.de/me/Portaldata/25/Resources/dokumente/publikationen/16-25.pdf

Ziehen wir trotzdem ruhig 1 Größenordnung ab, wir könnens uns ja leisten. ;)

Der Teil, der übrigens nicht vor den Auswirkungen der kosmischen Strahlung geschützt ist, d.h. die Außenschichten, ist gerade und übrigens so ziemlich der gleiche Teil, der später beim Wiedereintritt in die Atmosphäre eh verglüht bzw. noch stark genug erhitzt wird, dass Bakterien verrecken.

perttivalkonen schrieb:Wenn ich da jetzt mal die Nullen zusammenzähle, die ich für die ganze Reise von Anfang bis Ende abziehen muß, dann komm ich auf 5+3+1+4+1+6+4.

Naja, was soll bei einer Milchmädchenrechnung, die vom absoluten Worst-Case-Szenario ausgeht, auch anderes rauskommen? Was sind das für Zahlen? Wo kommen sie her? Welche Formel liegt hier zugrunde? Inwieweit sind die Zahlen durch Studien belegt? Von welchen Prämissen usw. wird ausgegangen? Etc. pp. Selbst die Drake-Gleichung bietet mehr, ist aber auch so'ne Milchmädchenrechnung. Der Einfachheit halber schlug ich ja schon eine Unterteilung vor: Auswurf, Transit, Eintritt. Mit den Warscheinlichkeiten p(A), P(T), p(E) für's Überleben einer Entität während einer dieser Phasen ließe sich über das Produkt dann die Gesamtwahrscheinlichkeit ausrechnen. Wobei hier nicht nur Unsicherheitsfaktoren (Interquartilsabstand) mit zu berücksichtigen wären, um die Wahrscheinlichkeiten für Best-, Average- und Worst-Case-Szenarien abschätzen zu können, sondern auch diverse zugrundegelegte Annahmen.

So aber bin ich von solchen Milchmädchenrechnungen herzlich wenig beeindruckt.

Die Einteilung in Phasen reicht auch nicht. Man kann sich so einen Meteorit/Asteroid bspw. in einem Schalenmodell veranschaulichen (und für unsere Zwecke tut's auch ein simples Atommodell):

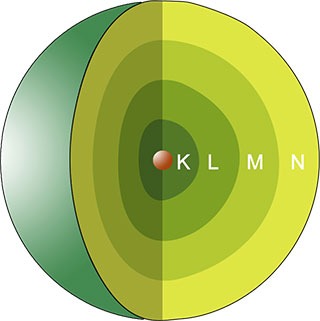
Die äußere Schicht N geht schon in der ersten Phase (Aufwurf) flöten, vor allem durch Ablation. Die Oberfläche von M wird zwar auch noch stark erhitzt, wird aber nicht mehr abgetragen. Bakterien in Schichten K und L fühlen sich auf jeden Fall pudelwohl, vielleicht auch noch ein paar in Schicht M. Schicht M ist insbesondere auch der kosmischen Strahlung ausgesetzt, Bakterien in Schichten K und L fühlen sich aber weiterhin pudelwohl. Beim Widereintritt in die Atmosphäre wird Schicht M übermäßig stark erhitzt und geht flöten (erneut durch Ableration). Schicht L wird zwar noch stark erhitzt, aber nicht mehr abgetragen. Bakterien in Schicht K (und vielleicht auch ein paar in Schicht L) fühlen sich pudelwohl.

"Pudelwohl" ist zwar stark übertrieben, aber so oder so ist es unzulässig, alle Wahrscheinlichkeiten und Szenarien von Anfang bis Ende gleichverteilt auf alle Schichten anwenden, denn ein innerer Teil ist von diversen Prozessen ab einer kritischen Mindestgröße überhaupt nicht betroffen.

perttivalkonen schrieb:Und dann stellt sich natürlich die Frage, ob das Bakterium auf Mars, Europa, Venus oder Enceladus nicht doch noch die Hufe hochreißt, weil ihm die dortigen Bedingungen nicht so recht schmecken.

Damit fügst du mit dem Szenario "langfristiges Überleben" in obiger Gleichung natürlich noch einen Faktor hinzu, womit eine andere Fragestellung gegeben ist. Explizit wollte der Diskussionsleiter scheinbar auf zwei Fragestellungen hinaus:

Alteiche schrieb am 27.10.2019:Was meint ihr wie wahrscheinlich ist es für euch, dass Leben es von der Erde auf die anderen Himmelskörper geschafft hat und dort bis heute überlebt haben?

Diese Fragen kann man zusammen betrachten, muss man aber nicht. Um die Diskussion auch überschaubar zu halten, würde ich die Frage nach den allgemeinen Bedingungen für Leben aber erst einmal ausklammern, da es - als notwendige Voraussetzung für die Entstehung von Leben - bereits an anderer Stelle zur Genüge diskutiert und untersucht wird.

perttivalkonen schrieb:Wie viele Impakte mit der Fähigkeit, irdisches Material ins All zu schleudern, kann es da in sagenwirmal den letzten 3 1/2 Milliarden Jahren existierenden Lebens auf der Erde gegeben haben? Eindeutig weniger als die für den Mars hochgerechneten 1400 Impakte.

Ich würde die Anzahl derartige Einschläge auch lieber vorsichtig auf 500-1000 schätzen.

perttivalkonen schrieb:Ich befürchte, es sind gar nicht so viele. [...] Vielleicht findest Du ja bessere Angaben.

Nach einer Abschätzung oder gar Zahlen musste ich lange suchen... Aber wie der Zufall nach dutzenden Papers so will...

"The ejecta size is important because of their ability to achieve radiation shielding against the Galactic cosmic ray nuclei. It requires ejecta with radii larger than 0.2m, and the survival increases with ejecta size. [...] The largerthe ejecta, the larger the portion that remains<100°C. Approximately 4×10^12 ejecta of this size range with T<100°C were ejected on average, in all directions, from Mars’ surface during the last 4 Gyr by impactors of diameters 1–20 km, i.e., an average∼10^9 per Myr (Mileikowsky et al. 2000)."
https://iopscience.iop.org/article/10.1088/0004-637X/690/1/210/meta

Hierbei reden wir aber nur über das Material, welches über alle Zeiten in alle möglichen Richtungen flog, aber darum ging es ja.

perttivalkonen schrieb:Wenn einer sagt, da gibts Aussterberaten von 10^(-4)...10^(-7), dann halte ich dem entgegen, daß das nur für einen Faktor bei einem Transspermie-Event gilt.

Berechtigter Einwand, nur sind aber eben auch nicht alle Teile von so einem Brocken gleichermaßen von allen Faktoren betroffen.

perttivalkonen schrieb:Wenn jemand auf die Menge von Mikroorganismen in einem Gramm Boden verweist, geh ich da sachbezogen drauf ein. Spricht jemand von Gigatonnen Auswurfmaterial, recherchiere ich und versuche, echte wissenschaftliche Hochrechnungen auszuwerten.

Wenn man obige Zahlen grob überschlägt... 4x10^12 Geschosse... r=0.2m... da käme man bei einer Dichte von 2,7t/m^3 auf ca. 134 Mrd. Tonnen, die da durch die "Luft" fliegen. Und wenn von diesem ggf. kontaminierten Material auch nur eine einzige Tonne, was nur dem winzigen Bruchteil von 0.0000000007% entspricht, auf einem anderen Planeten landet, käme das faktisch einer Invasion gleich.

Noumenon schrieb:Die Hitze beschränkt sich nur auf die äußeren Schichten eines Gesteinsklumpen, also die 5cm, von denen du ja bereits gesprochen hattest.

Von der Hitze hab ich an der Stelle doch gar nicht gesprochen. Sondern hiervon:

perttivalkonen schrieb am 30.10.2019:Bei einer Beschleunigung wird Druck aufgebaut, bei einer geradezu instantanen Beschleunigung auf Fluchtgeschwindigkeit ein geradezu immenser Druck. Beim Druckaufbau wird Wärme erzeugt, bei immens kurzzeitigem und immens starkem Druckaufbau eine immens hohe Temperatur erzeugt.

Und für diese Hitze gilt eben nicht Dein:

Noumenon schrieb:Der Druck (bis zu 50 GPa) breitet sich faktisch durch's gesamte Material aus, für die Temperatur gilt das allerdings nicht

Diese Hitze ist überall da, wo dieser Druck vorherrscht. Also "faktisch durch's gesamte Material"

Noumenon schrieb:Auch das hängt von diversen Faktoren ab, so dass man hier keine pauschale Aussage treffen kann. Temperaturausgleich findet bspw. nur über Strahlung und Leitung (im Inneren des Himmelskörpers) statt, nicht aber durch Konvektion, da Vakuum. Hauptsächlich wird Wärme in Form von Strahlung abgegeben, aber eben auch aufgenommen (=> Sonne, Wärmestrahlung).

Am Ende steht die Abkühlung. Völlig egal, wie lang das dauert.

Noumenon schrieb:Die Temperatur des Himmelskörpers hängt vor allem (aber nicht nur) von zwei Faktoren ab: Abstand zur Sonne und Reflexionsvermögen des Himmelskörpers. In einer Entfernung von 1 AE (also Erdnähe) würde die mittlere Temperatur eines Himmelskörpers mit ähnlichem Reflexionsvermögen wie dem der Erde bspw. um die -15 bis -20 Grad Celsius betragen.

Ja klar. Wenn das Objekt dann auf ungefähr dem Erdorbit bleibt. Dumm nur, daß es dann auch keinen anderen Himmelskörper erreichen wird. Dazu sollte es dann doch nen stärker elliptischen Umlauf um die Sonne vorlegen. Und somit auch größere Arschkälte abkriegen.

Noumenon schrieb:Die Rotation spielt durchaus eine entscheidende Rolle

Also ich gehe mal nicht davon aus, daß ein zenti-, dezi oder metergroßes Objekt ne Rotation von mehreren Stunden vorlegt. Dürfte eher kürzer sein. Alles in allem ignorier ich da mal nennenswerte Temperaturunterschiede bei. Vor allem im Innern; außen is ja eh schon alles tot.

Noumenon schrieb:Und obwohl die mittlere Temperatur eines Himmelskörpers in der Nähe des Mars (ca. 1,5 AE) aufgrund der Entfernung zur Sonne so um die -50°C liegt, kann sie auf Schattenseite bis auf -100°C runtergehen, während sie auf der Sonnenseite angenehme 20°C beträgt.

Klar doch, schlagartig ab Sonnenaufgang herrscht geschmeidiger Frühling auf jedem Fleckchen beschienener Mars. Nicht etwa erst Stunden später, und nur dort, wo die Sonnenstrahlen in leidlich steilem Winkel auf die Oberfläche treffen.

Noumenon schrieb:Dreht sich der Himmelskörper schnell genug (quasi wie ein Grillhähnchen über'm Lagerfeuer), verteilt sich die Temperatur mehr oder weniger gleichmäßig über den ganzen Körper (Worst-Case).

Worst Case? Echt jetzt?

Most asteroids with absolute magnitudes H > 22 (corresponding to D < 0.15 km) rotate with periods of less than 2 h.

https://www.lpi.usra.edu/books/AsteroidsIII/pdf/3016.pdf (Archiv-Version vom 30.11.2022)

Und das sind die Asteroiden, die ihren Spin von ihrer Bildung her haben. Wir aber sprechen von Material, welches durch einen Impakt von der Erde fortgeschleudert wird. Da hat quasi alles nen Spin.

Kaum daß ich angefangen habe, Deinen Beitrag zu lesen, stolpere ich von einer haltlosen Phantasterei zur nächsten. Es kann doch nicht angehen, daß Du Dir Deine Argumente einfach nur ausdenkst. Ausdenken ist ja in Ordnung, aber bevor man das dann anderen argumentativ vorhält, sollte man das dann durchaus mit der Realität abgleichen. Kann aber nicht angehen, daß ich hier Deine Hausaufgaben mache und für Dich die ganze Recherchearbeit leiste.

Daher beende ich es hier. Komm wieder, wenn Du was anderes vorzubringen hast, als zusammengereimten Schei*.