Erst einmal kurz zu den Grundbegriffen, sofern Du Dir diese nicht schon selbst angeeignet hast:
Mit "Knoten" werden die Punkte in solchen Strukturen bezeichnet, mit "Kanten" die Linien, die die Knoten/Punkte verbinden. Formal ausgedrückt sind die Knoten Elemente der Menge V ('vertices') und die Kanten Elemente der Menge E ('edges'), die zusammen den Graphen bilden (also ein Tupel (V,E)).
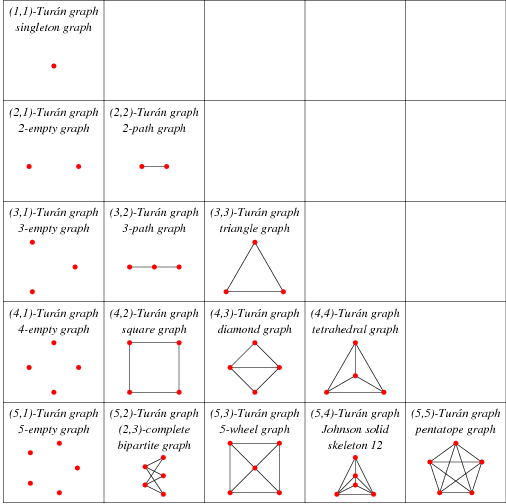
So, der Satz von Turán besagt nun, dass ein Graph unter der Bedingung, dass alle n Knoten nicht durch Kanten Dreiecke bilden können, eine maximale Anzahl an Kanten enthält (sprich dadurch nach oben beschränkt wird), nämlich [n^4/4], wobei die eckige Klammer bedeutet, dass nach unten abgerundet wird. Man verzeih mir diese unsaubere Schreibweise, aber der mir bekannte Formeleditor kennt keine Abrundungsfunktion.
Betrachte dazu die Grafik auf der entsprechenden Wikipedia-Seite:
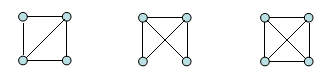
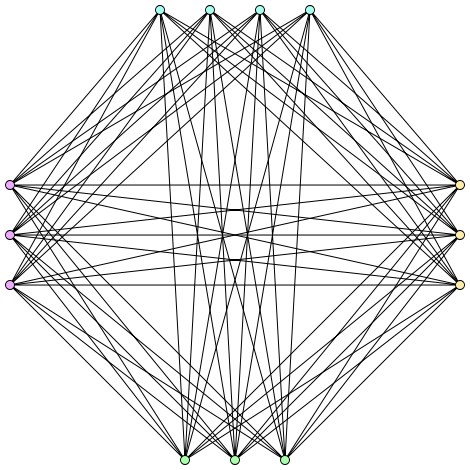
Alle drei Graphen besitzen n = 4 Knoten, allerdings 5 bzw. 6 Kanten. Setzen wir den Wert nun in die obige Formel ein, erhalten wir
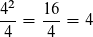
D.h. ein Graph mit 4 Knoten dürfte höchstens 4 Kanten haben, damit es möglich ist, eine solche Struktur ohne Dreieck zu zeichnen.
Beim ersten Graphen ist schnell zu sehen, dass kein Dreieck existiert, wenn man die Kante in der Mitte entfernt. Beim zweiten existiert aber bspw. immer noch ein Dreieck, nachdem man eine der Kanten in der Mitte entfernt hat. Dies widerspricht jedoch der Aussage des Satzes nicht, da diese lediglich eine obere Schranke ('höchstens') angibt, andernfalls würde man "genau dann, wenn ..." als Formulierung verwenden. Mit anderen Worten: Es war möglich, einen dreiecklosen Graphen zu konstruieren, der (höchstens) 4 Kanten besitzt, wie man am ersten sehen konnte.
Abschließend zu deinem Link:
https://oeis.org/A033437Diese Zahlenfolge enthält in aufsteigender Ordnung die besagten, aus der obigen Formel generierten Werte, die die obere Schranke (d.h. maximale Anzahl an Kanten) bildet.
Dazu kurz als Beispiel:
Die ersten zwei Werte sind 0, was logisch ist, da n=0 -> [0^2/4] = 0 sowie n=1 -> [1^2/4] = 0 ergibt. Selbiges gilt für n = 2 -> 1; dies ist alles ebenfalls der Wikiseite zu entnehmen. Abweichungen gibt es dann allerdings schon ab n=3. Ich kann mir vorstellen, dass dies daran liegt, dass der Graph auf oeis.org 5-partitiv ist, dies dagegen in dem Wikipediabeispiel nicht näher definiert ist. Da ich persönlich nur einige Grundlagen der Graphentheorie kenne, müsste ich mich da selbst einarbeiten, wofür mir leider die Zeit fehlt. Ich hoffe aber, dass ich Dir trotzdem helfen konnte, da das Konzept an sich klar ist.
Um das ganze visuell darzustellen, empfiehlt sich wohl, ein Programm zu schreiben. In Verbindung mit dem Studium des mathematischen Beweises sollte sich ein klareres Verständnis ergeben.
Warum interessiert dich das eigentlich?