@Peter0167 Das Problem ist, dass Elektronen keine "Kugeln" sind, die zusammenstoßen können. Elektronen haben keinen Radius, keine Ausdehung. Sie sind aber auch nicht unendlich kleine Punkte. Elektronen sind Quantenobjekte, und das ist extrem schwierig zu erklären. Es gibt nämlich in unserer Erfahrung nichts Vergleichbares.
Ein großes Problem dabei ist mit Sicherheit, dass man üblicherweise solchen Unsinn wie "Elektronen sind Welle und Teilchen gleichzeitig" hört, was das Verständnis nur noch erschwert. Elektronen sind nämlich weder Teilchen, noch Welle, sondern eben ein Quantenobjekt. Ein solches Quantenobjekt lässt sich in bestimmten Extremsituationen durch eine Welle oder durch ein Teilchen annähern, das ist richtig. Aber es ist und bleibt ein Quantenobjekt.
Mathematisch ist ein Elektron etwas unglaublich Abstraktes. Das Objekt, das seinen Zustand beschreibt ist ein Funktional, also eine Abbildung von einem Funktionenraum. Das irgendwie zu deuten ist nicht trivial.
In
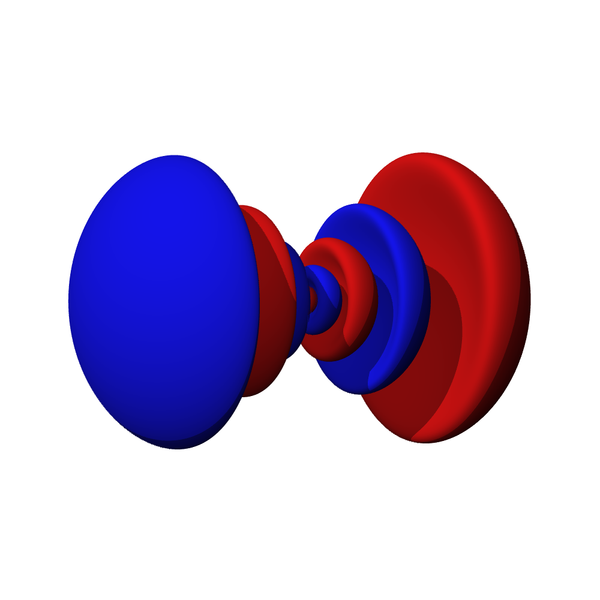
manchen Fällen ist es jedoch möglich, diese Abbildung mit einer bestimmten Funktion zu assoziieren. Das kannst du dir dann wie eine "Wolke" im Raum vorstellen. Orbitale sind z.B. solche Wolken. Die Grafiken, die du dazu meistens siehst sind zwar wiederrum nur eine reduzierte Darstellung dieser Wolke (es fehlen die reellen und komplexen Anteile, außerdem wird in der Regel nur einen Potentialfläche gezeichnet), aber können dir dir doch eine Vorstellung von der "Form" eines Elektrons geben.
Das Entscheidende ist nämlich das: Die Wirkung des Elektrons ist überall in dieser Wolke
gleichzeitig. Es ist kein kleiner Punkt, der zufällig hier und da erscheint, sondern diese Wolke
ist (von einem gewissen Standpunkt aus betrachtet) das Elektron.
Du weiß damit also, wie ein Elektron "aussieht", wenn es sich in einem Atom befindet. Und wenn ein Elektron frei im Raum herumflitzt, dann hat es auch eine gewisse "Form", also eine solche Wolke, die damit assoziiert werden kann.
Und diese Wolken sind (wiederrum in guter Näherung) die Objekte, die miteinander interagieren. Zwei kollidierende Elektronen sind also zwei solche Wolken, die in Wechselwirkung treten, weil sie sich zu "nahe" kommen.
Und was dabei passiert ist, sagen wir mal... kompliziert
;) In erster Linie kann man sagen, dass diese Wolken sich abstoßen. Das hat viele Gründe, z.B. sind die Wolken an das Photonenfeld gekoppelt. Darüber können sich Schwingungen übertragen, die dann die Wolken auseinandertreiben. Das ist das, was man dann als die elektrische Abstoßung der Elektronen wahrnimmt. Es gibt aber noch andere Effekte, die die Wolken sich abstoßen lassen. Viele dieser Effekte (z.B. Fermidruck) treten spürbar auf, wenn die Wolken sich stark überlappen, also ganz eng beieinander sein. Insgesamt könnte das dann so aussehen:
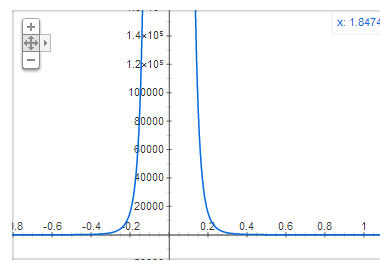
Das soll jetzt mal die Kraft sein, die die Elektronen auseinandertreibt, wenn sich die Wolken zunehmend stark überlappen. Du siehst, dass die Kraft extrem groß wird, wenn die Entfernung klein wird, darüber aber winzig klein ist.
Und eine solche Kraft sieht von außen aus, als ob die Teilchen zusammenprallen. Erst gibt es nämlich eine nicht wahrnehmbar kleine Kraft, und dann ist sie auf einmal riesig, woraufhin sie sich sofort wieder voneinander entfernen.
Wenn du jetzt Elektronen kollidieren lässt, dann sorgst du dafür, dass sie sich sehr nahe kommen. Bis zu einer bestimmten Energie siehst du nur einen normalen Stoß. Anhand der Bewegung nach diesem Stoß kannst du dem Elektron dann einen "Radius" zuordnen. Du tust also so, als ob diese Kraft unendlich steil wäre, und somit eine Art "Wand" darstellt. In der Grafik z.B. bei 0.15 oder so.
Gibst du den Elektronen mehr Energie, dann baut sich in diesem Potential eine ziemliche Menge Energie auf, und das kann dann zu vielen anderen lustigen Sachen führen. Bestünde das Elektron z.B. aus wiederrum anderen Teilchen, dann würde man vermuten, dass diese irgendwann mal auseinanderbrechen, wenn man die Belastung nur groß genug macht. Das scheint aber nicht der Fall zu sein.
Man kann sogar nichtmal eine irgendwie geartete Richtungsabhängigkeit der Elektronen feststellen, die Wolke scheint also (bei einem ruhenden, kräftefreien Elektron) absolut symmetrisch zu sein. Deswegen sagt man, dass Elektronen rund sind. Aber wie gesagt, sie haben weder eine feste "Form" (diese hängt immer von dem ab, was das Elektron gerade macht), noch einen Radius. Das sind lediglich Hilfsgrößen, die in manchen Situationen ganz nützlich sein können.
Nebenbei bemerkt: Das was man so gemeinhin als Elektron betrachtet ist auch nur ein "Nebeneffekt" von komplexeren Vorgängen. Das Elektronenfeld an sich hat nämlich an sich keine "schweren Elektronen". Es wechselwirkt jedoch mit dem Neutrinofeld, wobei durch eine bestimmte Symmetriebrechung ein Objekt entsteht, das man dann als "Elektron" kennt
;) Aber es ist erstmal kein grundlegendes Objekt in unserem Universum.
Bekannter schrieb:Was heißt Teilchenmittelpunkt?