Hier mal ein qualitativer Beweis für die Instabilität eines solchen Objekts. Wenn die Masse als Fluid betrachtet werden kann (bei Planeten der Fall, bei Sternen sowieso), dann kann es ein solchen Objekt nicht geben.

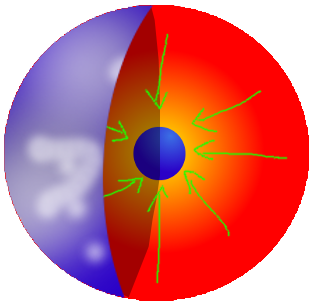
Wir sehen hier den Querschnitt eines Sterns mit einem Kern (orange) und einer Hülle (grün), die sich gemäß Renes Theorie abstoßen.
Ein Punkt in der Hülle ist exakt dann ohne Beschleunigung, wenn sich die auf ihn einwirkenden Kräfte exakt auslöschen. Rot eingezeichnet sind 14 exemplarische Kräfte, die sich auf der linken und auf der rechten Seite des Grafik befinden.
Diese Kräfte addieren sich zu F_ungestört auf, die exakt nach unten zeigt. Ihr entgegen wirkt F_abstoßung. Sie zeigt nach dem gleichen Prinzip exakt nach oben. Der Abstand zwischen Hülle und Kern ist dabei so eingependelt, dass die beiden Kräfte sich aufheben.
F_ungestört = F_abstoßung.
Nehmen wir jetzt eine Störstelle auf der linken Seite der Hülle an. Dies ändert die von dort ausgehende Gravitation. Wir nehmen o.b.d.a an, dass dort die Dichte höher sei, womit der gelbe Pfeil mehr Kraft repräsentiert, als sein Zwilling auf der rechten Seite. Es ergibt sich dadurch die Gesamtkraft F_gestört.
F_gestört hat im Gegensatz zu F_abstoßung eine horizontale Komponente. Dadurch gleichen sich die beiden nicht mehrt exakt aus und es bleibt eine nach links gerichtete Kraft auf das betrachtete Massenelement.
Da wir hier ein Fluid haben fließt nun also Masse von der rechten auf die linke Seite. Dadurch wird das Kräfteungleichgewicht weiter verstärkt und der Fluss erhöht sich weiter. Die Masse der Materie fließt somit auf die linke Seite, bis sich die Materie von der Antimaterie abscheidet und die beiden sich voneinander entfernen.
Das System ist somit labil und bricht bei der kleinsten Imhomogenität der Dichte oder Form zusammen.

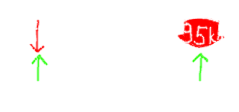
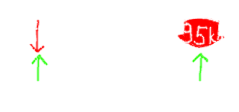




rene.eichler schrieb:Das liegt daran dass die Hülle mit ihrer 95% Masse ja Kugelsymetrisch ist und die Kraft Richtung Kugelmitte wirkt



rene.eichler schrieb:Das macht mir nichts aus, ich sag ja die Hülle und der kern drücken aufeinander