Schwarze Löcher
23.04.2019 um 17:00Hallo @Sonni1967,
Ich möchte es nocheinmal in anderen Worten erklären. Die maximale erreichbare Fallgeschwindigkeit bei freiem Fall geht gegen die FLuichtgeschwindigkeit erreicht diese aber aus endliche Höhe nie exakt. Der Ansatz wie man zu diesen Aussagen klommt ist einfach: DIe potentielle Energie wird in kinetische Energie umgewandelt.
Ein ganz einfaches Beipiel:
DIe potentielle Energie eines Körpers gegenüber der Erde hängt ab von seinem Abstand zur Erdoberfläche h und seiner Masse:
Lassen wir diesen Körper aus einer Höhe h fallen können wir die Aufschlagsgeschwindigkeit berechnen. Das könne wir deshalb weil wir wiessen das die potentielle Energie in kinetische Energie umgewandelt wird:
Da die Masse links und rechts auftaucht kürzt sie sich raus und wir können nach v auflösen:
Du kannst nun für h beliebige Werte einsetzten und bekommst dann die Aufprallgeschwindigkeit heraus. Du könntest die FOrmel auch umstellen nach der Höhe h und berechnen wie hoch eine Kugel fliegt bei einer bestimmten vertikalen Abschussgeschwindigkeit. Doch was passiert mit v wenn wir die Hohe h gegen unendlich gehen lassen? In dem Fall würde auch v gegen unendlich gehen
denn v(\infty) = \sqrt{2g \infty} = \infty.
Was haben wir falsch gemacht? Die Erdbeschleunigung g ist natürlich auch von der Höhe h abhängig und nur bei geringen Abständen von der Erdoberfläche konstant. Daher heißt unsere Formel besser
Für große Höhen h h \rightarrow \infty geht g(h) \rightarrow 0. In Worten auf der Erdoberfläche ist g = 9,81 m/s2, in 10 km Höhe beträgt diese nur noch 4 m/s2 und geht bei noch größeren Höhen gegen null.
Wikipedia: Schwerefeld#Erdschwerefeld außerhalb der Erde
Was passiert jetzt mit v(h) für Höhen h gegen unendlich? Nun die obere Formel hilft uns hioer nicht mehr denn wir erhalten:
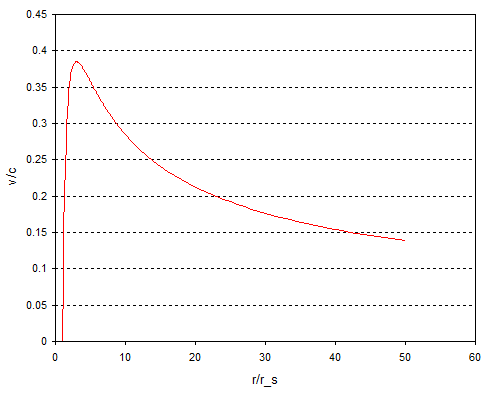
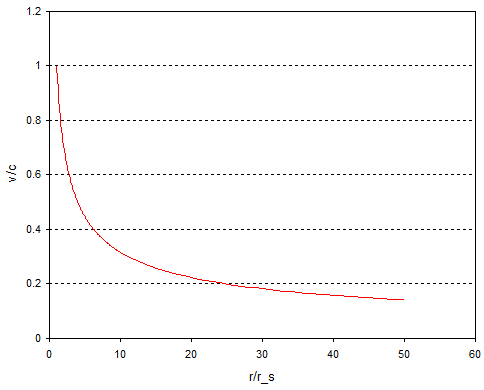
Um nun also den Grenzwert zu berechnen der Maximal möglichen Aufschalgsgeschwindigkeit, müssen wir über die Höhe h integrieren so wie das hier gemacht wird:
http://www.extycion.de/physik/files/exphys/ueb/blatt03/exph_ueb03.pdf (Archiv-Version vom 13.07.2017)
Aber keine Sorge das Prozedere ist genau dasselbe: Man berechnet die maximale potentielle Energie die eine Objekt gegenüber einer Masse erhalten kann. Und da die potentielle Energie mit der Höhe h zunimt ist die natürlich maximal in undendlicher Höhe h.
Ist die potnetielle Energie in unendlicher Höhe h unendlich? Nein. Kann daher die Aufschlagsgeschwindigkeit eines Massebheafteten Objektes c sein? Nein, den dafür müsste unendlich viel potentielle Energie zwischen Objekt und Masse vorhanden sein. Denn wir wissen
E_{kin} = E_{pot} und E_{kin} = (\frac{1}{\sqrt{1-v^2/c^2}}-1)mc^2 für v rightarrow c folgt E_{kin} = (\frac{1}{\sqrt{1-c^2/c^2}}-1)mc^2 = \infty = E_{pot}
Ein massebahftetes Objekt kann die LG nicht erreichen. Genau so gut kann ein frei fallendes Objekt niemals schneller oder gleich der Fluchtgeschwindigkeit auf der Erde aufschlagen. Um Fluchtgeschwindigkeit beim Aufschlag zu erreichen müsste es aus unendliche Höhe fallen gelassen werden, was nicht geht. Genau das ist das Prinzip des Grenzwertes: geht gegen einen endlichen Wert.
@all
Ein massebehaftetes Objekt das sich mit v = c im Raum bewegen würde, würde sich mit v > c in der Raumzeit bewegen.
@hawak hat das hier schön ausgedrückt:
Richtig.Sonni1967 schrieb:Die Fluchtgeschwindigkeit ist die Geschwindigkeit die ein Objekt brauch um der Anziehungskraft (dem Gravitationstopf) eines
Himmelkörpers zu entkommen (sodass er nicht mehr zurückkehren muss)
Im groben richtig. Allerdings hängt die Fluchtgeschwindigkeit auch vom Abstand zur Masse ab. Dazu gleich noch mehr.
größer muss auch die Fluchtgeschwindigkeit sein
LG eines massebhaftetes Objektes tritt gar nicht ein, dafür benötigt es unendlich viel Energie.
Ich möchte es nocheinmal in anderen Worten erklären. Die maximale erreichbare Fallgeschwindigkeit bei freiem Fall geht gegen die FLuichtgeschwindigkeit erreicht diese aber aus endliche Höhe nie exakt. Der Ansatz wie man zu diesen Aussagen klommt ist einfach: DIe potentielle Energie wird in kinetische Energie umgewandelt.
Ein ganz einfaches Beipiel:
DIe potentielle Energie eines Körpers gegenüber der Erde hängt ab von seinem Abstand zur Erdoberfläche h und seiner Masse:
E_{pot} = mgh
Lassen wir diesen Körper aus einer Höhe h fallen können wir die Aufschlagsgeschwindigkeit berechnen. Das könne wir deshalb weil wir wiessen das die potentielle Energie in kinetische Energie umgewandelt wird:
E_{pot} = mgh = \frac{1}{2}m v^2 = E_{kin}
Da die Masse links und rechts auftaucht kürzt sie sich raus und wir können nach v auflösen:
v(h) = \sqrt{2gh}
Du kannst nun für h beliebige Werte einsetzten und bekommst dann die Aufprallgeschwindigkeit heraus. Du könntest die FOrmel auch umstellen nach der Höhe h und berechnen wie hoch eine Kugel fliegt bei einer bestimmten vertikalen Abschussgeschwindigkeit. Doch was passiert mit v wenn wir die Hohe h gegen unendlich gehen lassen? In dem Fall würde auch v gegen unendlich gehen
denn v(\infty) = \sqrt{2g \infty} = \infty.
Was haben wir falsch gemacht? Die Erdbeschleunigung g ist natürlich auch von der Höhe h abhängig und nur bei geringen Abständen von der Erdoberfläche konstant. Daher heißt unsere Formel besser
v(h) = \sqrt{2g(h)h}
Für große Höhen h h \rightarrow \infty geht g(h) \rightarrow 0. In Worten auf der Erdoberfläche ist g = 9,81 m/s2, in 10 km Höhe beträgt diese nur noch 4 m/s2 und geht bei noch größeren Höhen gegen null.
Wikipedia: Schwerefeld#Erdschwerefeld außerhalb der Erde
Was passiert jetzt mit v(h) für Höhen h gegen unendlich? Nun die obere Formel hilft uns hioer nicht mehr denn wir erhalten:
v(\infty) = \sqrt{2g(h)h} = \sqrt{2 \cdot 0 \cdot \infty} \rightarrow~keine~vernünftige~Aussage
Um nun also den Grenzwert zu berechnen der Maximal möglichen Aufschalgsgeschwindigkeit, müssen wir über die Höhe h integrieren so wie das hier gemacht wird:
http://www.extycion.de/physik/files/exphys/ueb/blatt03/exph_ueb03.pdf (Archiv-Version vom 13.07.2017)
Aber keine Sorge das Prozedere ist genau dasselbe: Man berechnet die maximale potentielle Energie die eine Objekt gegenüber einer Masse erhalten kann. Und da die potentielle Energie mit der Höhe h zunimt ist die natürlich maximal in undendlicher Höhe h.
Ist die potnetielle Energie in unendlicher Höhe h unendlich? Nein. Kann daher die Aufschlagsgeschwindigkeit eines Massebheafteten Objektes c sein? Nein, den dafür müsste unendlich viel potentielle Energie zwischen Objekt und Masse vorhanden sein. Denn wir wissen
E_{kin} = E_{pot} und E_{kin} = (\frac{1}{\sqrt{1-v^2/c^2}}-1)mc^2 für v rightarrow c folgt E_{kin} = (\frac{1}{\sqrt{1-c^2/c^2}}-1)mc^2 = \infty = E_{pot}
Ein massebahftetes Objekt kann die LG nicht erreichen. Genau so gut kann ein frei fallendes Objekt niemals schneller oder gleich der Fluchtgeschwindigkeit auf der Erde aufschlagen. Um Fluchtgeschwindigkeit beim Aufschlag zu erreichen müsste es aus unendliche Höhe fallen gelassen werden, was nicht geht. Genau das ist das Prinzip des Grenzwertes: geht gegen einen endlichen Wert.
@all
Ein massebehaftetes Objekt das sich mit v = c im Raum bewegen würde, würde sich mit v > c in der Raumzeit bewegen.
@hawak hat das hier schön ausgedrückt:
Der Grund dafür ist einfach: In der SRT bewegen sich ausnahmslos alle Objekte mit der LG durch die Raumzeit.hawak schrieb:Ein Objekt mit Ruhemasse > 0 kann c unter keinen Umständen erreichen, während sich ein Objekt mit Ruhemasse 0 immer und unter allen Umständen mit c bewegen muss.
