Die Relativitätstheorie

@uatu | @pluss |@delta.m | @skagerak | @mojorisin

So hier mal der Link zu AstroNews: Das "Photon"-Paradoxon oder wie die Richtung eines Photons umkehrt

@nocheinPoet

nocheinPoet schrieb:So hier mal der Link zu AstroNews:

Der Vorteil am oberen Bild ist das die Beschleunigungen rausfallen und man damit nur mit ganz normalen Lorenztransformationen arbeiten kann.

@mojorisin

Geht aber genau so einfach ins System von Carl. Oder sieht Du das anders?

nocheinPoet schrieb:Geht aber genau so einfach ins System von Carl. Oder sieht Du das anders?

Ja geht genau so einfach. WEnn hier jatzt mal noch jeamnd das ganze ausrechnen würde wärs prima :-)

@mojorisin

Würde ich machen, Du hast ja nun schon Bild gepinselt, aber mir fehlt aktuell echt die Zeit, dürfte hier gar nicht lesen und schon gar nicht schreiben, werde wohl noch bis in die Nacht basteln müssen.

mojorisin schrieb:Der Vorteil am oberen Bild ist das die Beschleunigungen rausfallen und man damit nur mit ganz normalen Lorenztransformationen arbeiten kann.

Dann löse deine dort aufgeführten "Fragezeichen" doch mal mit Hilfe der Lorenztransformation.

@mojorisin

mojorisin schrieb:Alice bewegt sich hier mit 0,7c nach links, das Photon schnurstracks nach oben.

Ich will hier nicht nerven,
aber bei Deiner neuen Zeichnung will es mir nicht in den Kopp, dass für Bob cy = c sein soll .

Ich kapier's nicht :(

@mojorisin

Das "Problem" ist, man könnte immer neu anfangen, man nimmt sich das System von Bob oder Carl als Startpunkt und baut drauf auf. Ich drehe noch immer am Ende die Flugrichtung vom Photon auf der y-Achse um ... :D

Also so im Kopf. Echt wo knifflig, dass man dazu auch gar nicht konkretes wo im Netz findet, ich kann doch nicht der Erste sein, der sich so einen Käse überlegt ...

delta.m schrieb:aber bei Deiner neuen Zeichnung will es mir nicht in den Kopp, dass für Bob cy = c sein soll .

Ich kapier's nicht :(

Das liegt an der Zeitdilatation.

@delta.m

Was soll es denn für Bob sonst sein? Generell ist es in der SRT so, dass sich ein Photon in jedem System mit c bewegt. Bob hat in seinem System ein Photon und das bewegt sich nur auf der y-Achse, da muss v = c sein. Was sonst?

@nocheinPoet

nocheinPoet schrieb:Bob hat in seinem System ein Photon und das bewegt sich nur auf der y-Achse, da muss v = c sein. Was sonst?

Ach so, es hat also jetzt keinen Winkel mehr zur x-Achse so wie beim ersten Bild von mojo(?)

@delta.m

Genau, stell Dir vor Du bist im Bahnhof ein Zug fährt langsam an Dir vorbei, ein Junge im Zug lässt einen Ball auf und ab springen. Für Dich macht der eine Zickzack Bewegung. Nun läufst Du los, genauso schnell wie der Zug, Du läufst mit gleicher Geschwindigkeit wie der Zug durch den Bahnhof und nun macht der Ball des Jungen für Dich nur wieder eine auf und ab Bewegung.

Nun fülle den Bahnhof mit viel Nebel, nimm Zug, Bahnhof und den Jungen weg und behalte nur den Ball ... :D Und betrachte den auch nur auf seiner Bewegung nach oben. Das mit der Gravitation musst Du auch noch mal vergessen, und dann passt es. Also mit dem Ball, beim Photon ist es etwas anders, da muss die Summe der Geschwindigkeiten eben immer genau c ergeben.

Und bedenke, in Deinem Ruhesystem gibt es keine Zeitdilatation für Dich, Du hast da immer Eigenzeit, die Zeit geht in Deinem System für Dich nie langsamer. Und das ist gleichberechtigt so. Heißt, nur in einem bewegten System geht für Dich die Zeit langsamer, in diesem System ist es genauso, dort geht dann die Zeit in Deinem System langsamer.

Ganz wichtig, die Zeitdilatation so in der SRT ist bei zwei zueinander bewegten Systemen nie absolut. Heißt, für Alice geht die Zeit in den Ruhesystemen von Carl und Bob langsamer, aber für Carl und Bob geht die Zeit von Alice langsamer.

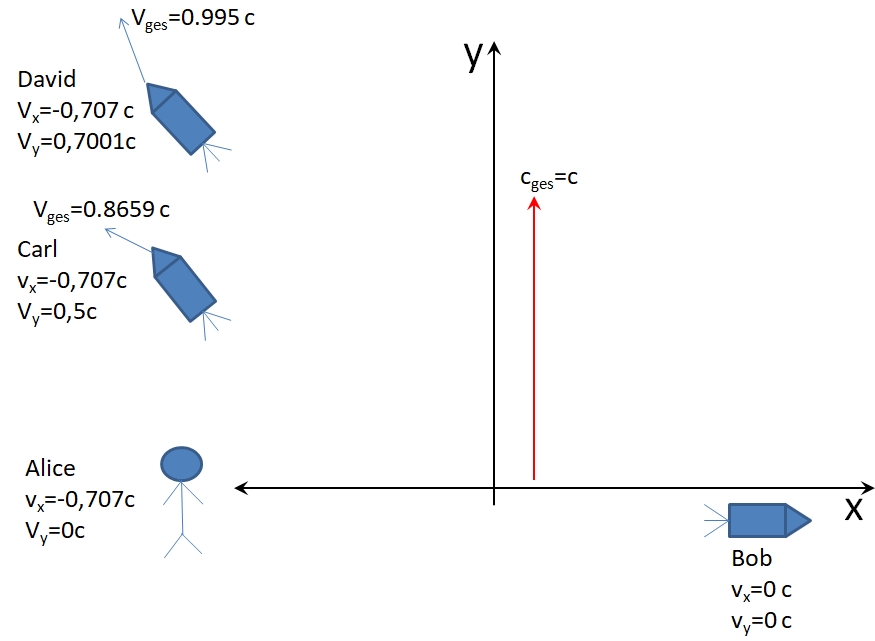
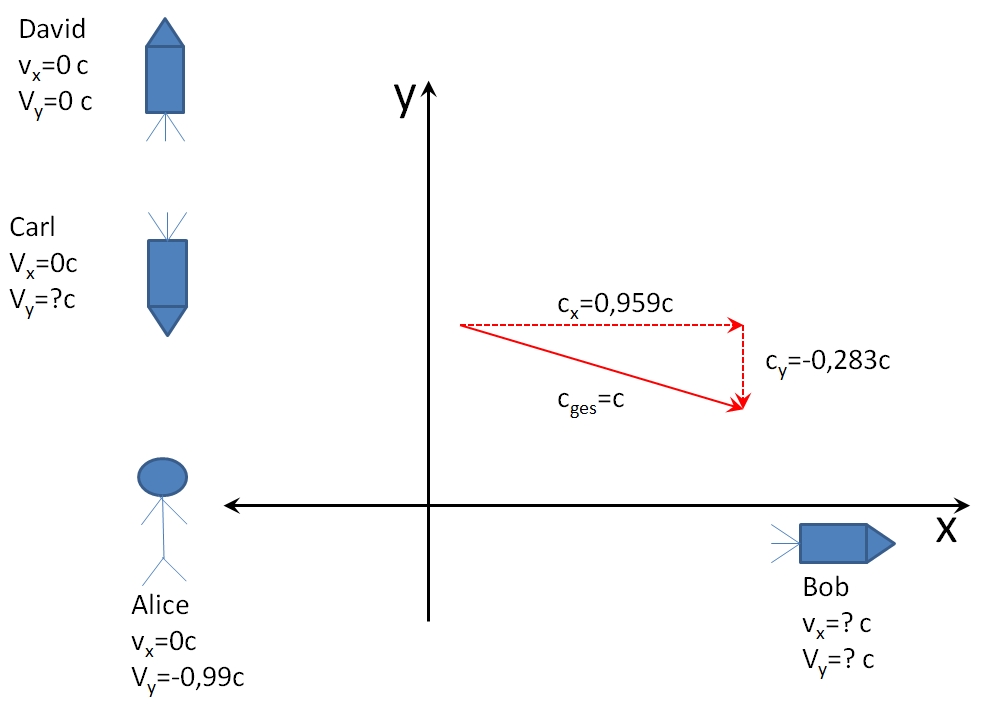
Also um die Fragezeichen aus dem oberen Bild zu beantworten:

Im Ruhesystem von Bob bewegt sich ALice mit v_x = -0,707 c. Da Carl und David relativ zu Alice auf der x-Achse ruhen sind deren x-GEschwindigkeiten ebenfalls v_x = -0,707 c.

Wir wissen das weil sich das Ruhesystem von ALice und von Bob entlang der x-Achse gegeneinander bewegt und zwar aus Sicht von Bob mit -0,707c. Wir können diese Relativgeschwinsdigkeit zwischen den Systemen miz u bezeichen , d.h. u = -0,707c. Wir wissen daher schon mal:




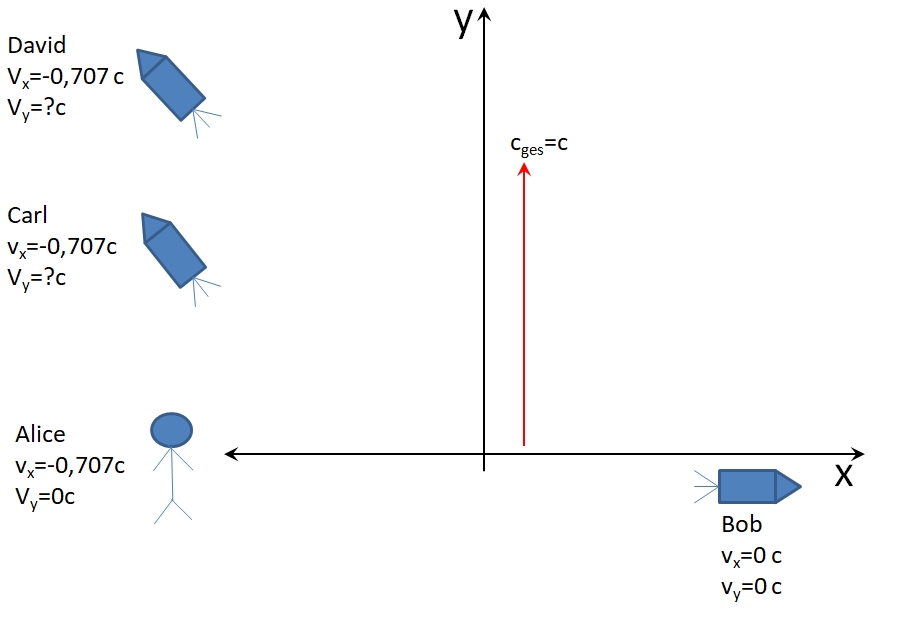
Nun können wir diese INfo nutzen und noch die y-GEschwindigkeiten von David und Carl berechnen wie sie Bob sieht. v'_x ist dabei die Geschwindigkeit wie sie sich aus dem System von Alice ergibt.

Für Carl:


daraus ergibt sich eine Gesamtgeschwindigkeit für Carl:


Für David:


daraus ergibt sich eine Gesamtgeschwindigkeit für David:



DAs ganze Spiel kann man jetzt auch machen aus Sicht von Carl bzw. aus SIcht von David.

Nun kann man sich fragen wie die gaz Geschichte aus Sicht von David aussieht:




Man sieht hier schon der Lichtstrahl aus Sicht von David geht nun nach rechts unten.

Und darum geht es hier auch: Wie kann es sein das Bob das Photon nach oben gehen sieht und David das Photon nach unten gehen sieht?

Eine Antwort darauf findet man wenn man sich die Struktur der Lorentztransformation anschaut. Mathamtisch kann man das analysieren anhand der Gruppentheorie. Das soll hier aber nicht abschrecken wirken. Die Gruppentheorie gibt uns ein Werkzeug an die Hand bei der wir schaune können ob bestimmte Transformationen dasselbe Resultat ergeben.

Ein ganz einfgaches Beispiel erhält man wenn man sich ein Quadrat anschaut. Welche Möglichkeiten gibt es ein Quadrat um seinen Ursprung zu rotieren so das wieder die Ecken auf sich selber abgebildet werden? Genau 4:



Eine Drehung um 360° bewirkt das dieselebn Ecken wieder auf sich selbst abgebildet werden.

--> Nun kommt der wichtige Punkt: Eine Drehung um 2 x 90° ist exakt dasselbe ist wie eine Drehung um 180°.

Was hat das nun mit unserem Beipiel zu tun? Nun die Frage ist wie kann es sein das Bob das Licht nach oben gehen sieht und David das Licht nach unten? Kann David das Licht überholen? Nein. Allerdings können Aneinanderreihungen von Lorenzboosts dasselbe bewirken wie Drehungen im Raum. Man kann sich das so klarmachen:

Setzen wir uns in das Ruhesystem von Bob: Von hier gibt es zwei Möglichkeiten in das Ruhesystem von David zu transformieren:

1. Lorentzboost in das System von Alice gefolgt von einem Lorentzboost in das System von David
--> Boost x Boost

2. Drehung des Koordinatensystems so das Davids Geschwindigkeitsvekor parallel zu einer der Koordinatenachsen liegt und dann Lorenzboost:
--> Drehung x Boost

Beide Möglichkeiten sind gleichwertig daraus folgt: Boost x Boost = Drehung x Boost

Das Erstaunliche ist also das Durchführen von mehreren Lorentztransformationen dieselben Auswirkugnen haben kann wie eine Drehung im Raum. Das ist mit den Galileitransformationen garantiert nicht der Fall.

@mojorisin
Sei mir nicht böse, aber ich bin raus, das ist mir zu komplex ;)

Ihr habt also das Paradoxon gelöst, mit den Lorentzboost´s, oder wie?

@skagerak

skagerak schrieb:Sei mir nicht böse, aber ich bin raus, das ist mir zu komplex ;)

Das ist kein Problem, die mathematische Struktur der Lorentzgruppe ist mit Sicherheit kein Einsteigerthema, sondern benötigt einiges an Einarbeitungszeit und etwas Grundlagenwissen in der Gruppentheorie.

skagerak schrieb:Ihr habt also das Paradoxon gelöst, mit den Lorentzboost´s, oder wie?

Lorentzboost heipt eigentlich nur Lorentztransformation. Was man von hier mitnehmen kann ist das Wissen das eine mehrmalige Lorentztransformation unter bestimmten Umständen (wenn sie nicht zweimal in die gleiche Richtung erfolgen) die gleichen Auswirkungen hat wie eine Drehung des Raumes.

Genau dieser Sachverhalt heißt in Lehrbüchern dann: räumliche Drehungen bilden eine Untergruppe der Lorentzgruppe.

Ja, damit sollte das Paradoxon aufgelöst sein.

mojorisin schrieb:Genau dieser Sachverhalt heißt in Lehrbüchern dann: räumliche Drehungen bilden eine Untergruppe der Lorentzgruppe.

Ja, damit sollte das Paradoxon aufgelöst sein.

Na dann, gut dass ich das denn weiß ;)

Lorentzboost heipt eigentlich nur Lorentztransformation.

Warum wird es denn boost genannt?

skagerak schrieb:Warum wird es denn boost genannt?

Das ist eine gute Frage und hab gerade erst gesehen:

Die speziellen Lorentz-Transformationen (auch Lorentz-Boosts oder nur Boosts), nach Hendrik Antoon Lorentz, sind eine Unterklasse der Lorentz-Transformationen. ...Formal sind sie diejenigen Lorentz-Transformationen, die keine Raumspiegelung, keine Zeitumkehr und keine Drehung beinhalten.

Wikipedia: Spezielle Lorentz-Transformation

delta.m schrieb:Ach so, es hat also jetzt keinen Winkel mehr zur x-Achse so wie beim ersten Bild von mojo(?)

Bob bewegt sich gegenüber Alice mit 0,707c. Aus Sicht von ALice bewegt sich also Bob genauso schnell entlang der x-Achse wie das Photon.
Um nun zu wissen wie schnell sich das Photon aus Bobs Sicht entlang der x-AChe bewegt müssen wir die Differenz berechnen:

Korrektur zu den FOrmeln im obigen Beitrag:

Beitrag von mojorisin (Seite 26)

Es werden natürlich die y-Geschwindigkeiten ausgerechnet.

Daher muss es in allen Berechnungen heißen: