Die Relativitätstheorie

nocheinPoet schrieb:So hier mal der Link zu AstroNews: Das "Photon"-Paradoxon oder wie die Richtung eines Photons umkehrt

Hehe, da nimmt man es aber genau:

Da wird nun drüber spekuliert,
ob das in y-Richtung pendelnde Photon in der Lichtuhr die Beschleunigung in x-Richtung mitmacht oder seitlich "rausfällt".

Ein Kommentar dazu:
Wenn es zu Beginn parallel zur y-Achse bewegt ist, wird dass so bleiben. Es bewegt sich nicht auf einmal in x-Richtung und “fällt daher seitlich raus”.

Würde zunächst auch dazu tendieren, dass es "rausfällt".

Wie ist hier die Meinung?

@delta.m

delta.m schrieb:Würde zunächst auch dazu tendieren, dass es "rausfällt".

Bei Beschleunigung gilt das Äquivalenzprinzip:





--> Es fällt raus

@mojorisin

So habe mal ein wenig hier gelesen, auch wenn ich wenig Zeit habe. Was mir auffällt, Du magst wohl richtig liegen, aber so wirklich geht es so nicht in meinem Kopf.

Gehe ich mal davon, dass wir da dann wo eine Drehung im Raum durch die beiden Beschleunigungen erzeugen. Dann haben wir doch eine reale Rotation, die Ausrichtung des einen System ist real im Raum anders. Schaut man aus dem Fenster sieht man nicht mehr den Punkt, den man vorher noch direkt vor Augen hatte.

Wie kann das sein, in welche Richtung dreht man sich, und bei einer Rotation müssten doch Zentripedalkräfte auftreten.

Weißt Du, die meisten Dinge der SRT kann ich mir auch real wo bildlich vorstellen, aber hier bekomme ich bisher nicht wirklich was klar hin. Vieles kann man ja auch visualisieren, wenn man eine Dimension raus nimmt, eine aus dem Raum oder auch zwei und dafür dann die Zeit als Raumdimension nimmt. So das "verdrehen" in der Zeit.

Aber hier scheint auch das nicht zu helfen, bisher finde ich da keinen Weg ein paar Autos über einen Parkplatz fahren zu lassen und dann hat sich aufmal eines gedreht.

Kann doch keine Rotation im vierdimensionalen Raum sein, so wie sich ein Hypercube umkrempelt. Ich kann doch nicht durch mich selber hindurch rotieren.

Also ich gehe mal aus, Du hast das von der Theorie und auch mathematisch gelöst, aber wirklich begreifen und logisches Verstehen stellt sich bei mir noch nicht ein. ;)

@delta.m | @mojorisin

Ja, im Grunde ist es so richtig, es "müsste" raus fallen. Aber das ist irrelevant für das eigentliche Szenario, darum kann man die Lichtuhr in der Rakete die beschleunigt für die Phase der Beschleunigung einfach anhalten und dann danach neu starten und schon passt es wieder. :D

@nocheinPoet

nocheinPoet schrieb:Gehe ich mal davon, dass wir da dann wo eine Drehung im Raum durch die beiden Beschleunigungen erzeugen.

Ich habe absichtlich die vier Beobachter eingeführt, so dass es keinerlei Beschleunigungen braucht. Dann kann man nämlich einfach über die normalen Lorentztransformationen gehen.

Bei diesem Beispiel benötigt es außerdem auf jeden Fall zwei Raumdimensionen, was die Sache unheimlich schwieriger macht, vor allem wenn man dann noch Beschleunigungen mitverarbeiten will. Man Suche nurmal nach 3D Minkowski-Diagrammen. Alles was ich da finde sind die Lichtkegel, aber keine zwei Bezugssystem übereinandergelegt.

@nocheinPoet

Ich kann mir vielleicht vorstellen wo der Knoten ist. Es erscheint unmöglich das man das Photon entlang der y-Achse überholen kann. UNd dasist es auch. Wie wir z.B. sehen ist aus SIcht von Bob:



David immer langsamer in y-Richtung als das Photon. Wir sehen aber auch in diesem Bild das Davids Rakete, aus Sicht von Bob nach links weggedreht erscheint. ALso hier mal nur die Drehung veranschaulicht:




In diesem Bild sieht man jetzt nur die Drehung. Für die vollständige Transformation kommt jetzt noch der Lorenz-Boost von 0,995c dazu, was dann aus Bobs Sicht klar erklärt das David den Lichtstrahl mit negativer y' Geschwindigkeit sehen muss.

Der Unterschied zur klassischen Mechanik ist versuche ich mal hier aufzuklären. Ein Photon kann sich immer nur mit c bewegen, d.h. wenn ich orthogonal zur Aubreitungsrichtung eines Photon beschleunige, verliert es an Vertikalgeschwindigkeit. Oder im Rahmen des ersten Bildes: Während sich das Photon für Bob parallel zur y-AChse bewegt, muss es für Alice an y-GEschwindigkeit einbüßen, da das Photon für Alice ja eine nichtverschwindende x-Komponente hat und die Gesamtsumme 1c ergebn muss

Bei klassichen Objekten ist das nicht der Fall; hier ein einfacher Vergleich:

Original anzeigen (0,2 MB)

Der Trick ist das im relativistischen Fall das Photon bei eine Quertransformation an vertikaler Geschwindigkeit "verliert" da die Gesamtsumme = 1 c sein muss. Das heißt es bleibt der Gesamtgeschwindigkeitvektor invariant.

Im klassischen Fall dagegen bleibt die Vertikalgeschwindigkeit konstant so dass sich der Gesamtgeschwindigkeitsvektor ändert. Im klassischen Fall kann aus Sicht von Bob nur ein Beobachter die Kugel in negativer y-Richtung fliegen sehen der sich aus Sicht von Bob mit v_y > 100 m/s bewegt.

Und hier liegen denke ich noch Vorstellungsschierigkeiten, denn in der SRT ist das nicht mehr notwendig. In der SRT ist es möglich das sich aus SIcht von Bob das Licht schneller in y-Richtugn bewegt als ein weiterer Beobachter. Dennoch kann aus Sicht des weiteren Beobachter das Licht sich in negativer y-Richtung bewegen.

mojorisin schrieb:Und hier liegen denke ich noch Vorstellungsschierigkeiten, denn in der SRT ist das nicht mehr notwendig. In der SRT ist es möglich das sich aus SIcht von Bob das Licht schneller in y-Richtugn bewegt als ein weiterer Beobachter. Dennoch kann aus Sicht des weiteren Beobachter das Licht sich in negativer y-Richtung bewegen.

Das klingt echt verrückt. Und wäre ich verrückt, würde ich behaupten dass wäre ein Dogma dass die Gesamsumme immer 1c ergeben muss ;)

Könnte man denn auch von sowas ähnlichem wie eine scheinbare negative y-Richtung sprechen?

@skagerak

skagerak schrieb:Könnte man denn auch von sowas ähnlichem wie eine scheinbare negative y-Richtung sprechen?

Nein, es ist tatsächlich so das man unterschiedliche Messungen erhält abhängig vom Bezugssystem. Das einfachste Beipiel ist die Längenkontraktion. Einen bewegten Zug mit 0,9 c würden wir tatsächlich kürzer messen, wir würden auch hier nicht von einer scheinbaren Länge bei bewegten Objekten sprechen. Bei hochenergetischen Elementarteilchen kann man dann schließlich auch die Auswirkungen der Lorentzkontraktion tatsächlich messen.

mojorisin schrieb:Nein, es ist tatsächlich so das man unterschiedliche Messungen erhält abhängig vom Bezugssystem.

Okay, das muss ich erst mal verdauen, das ist ja ähnlich kurios wie das Garagenparadoxon. Hat Euer Paradoxon denn auch etwas mit der Relativität der Gleichzeitigkeit zu tun, also keine Wahrnehmung ist absolut und so?

@skagerak

skagerak schrieb:. Hat Euer Paradoxon denn auch etwas mit der Relativität der Gleichzeitigkeit zu tun, also keine Wahrnehmung ist absolut und so?

Danke für den Einwurf, ich will hier mal Wikipedia zitieren:

Wikipedia: Paradoxon der Längenkontraktion

Das ursprüngliche Bild:


Die Auflösung:

Stab und Loch fliegen in diesem System nicht mehr parallel aufeinander zu. Daraus folgt erstens: Gleichzeitige Ereignisse in einem Inertialsystem laufen in einem anderen unterschiedlich schnell bewegten Inertialsystem nicht ebenfalls gleichzeitig ab, und zweitens sind „parallele“ Geraden im anderen Inertialsystem nicht mehr parallel: Der Winkel zwischen zwei Raumrichtungen wird von zwei sich relativ zueinander bewegenden Beobachtern unterschiedlich gemessen.

-------------------------------------

skagerak schrieb:Okay, das muss ich erst mal verdauen, das ist ja ähnlich kurios wie das Garagenparadoxon.

Allerdings lässt sich, im Gegensatz zum Thema hier, das Garagenparadoxon herrlich im Rahmen eines 2D Minkowski-Diagramms erklären. Mit etwas Zeit und Geduld kann man es dann hier sehr anschaulich verstehen:

http://wase.urz.uni-magdeburg.de/kassner/srt/pseudoparadoxa/stab_scheune/stab_scheune.html

@mojorisin
Ich habe für gewöhnlich auch nicht so die großen Schwierigkeiten, wenn ich mir physikalische Abläufe, auch bei relativ zueinander bewegten Objekten, bildlich vorstellen muss. Aber wie bei diesem Beipiel, wo wir nun zwei Raumdimensionen, mit zudem auch noch beschleunigten Objekten haben, wird es dann doch schon ziemlich tricky. Und wie Du ja auch schon angemerkt hast, dürften übereinandergelegte Bezugssysteme bei physikalischen Veranschaulichungen auch nicht gerade der Klassiker sein. ;)

Ich denke aber, daß Deine Erläuterungen und Bilder hierzu es für viele Mitleser nun wesentlich verständlicher machen konnten. :Y:

Libertin schrieb:Ich denke aber, daß Deine Erläuterungen und Bilder hierzu es für viele Mitleser nun wesentlich verständlicher machen konnten.

Also ich habe zumindest das Paradoxon verstanden, und dass es aufgelöst werden kann. Wie es das kann, eher weniger, aber ich akzeptiere es auch ;)

Danke @mojorisin :)

@mojorisin
Übrigens fand ich folgendes Video für mich hilfreich das Garagenparadoxon zu verstehen: Youtube - Garagenparadoxon

@Libertin

Libertin schrieb:Und wie Du ja auch schon angemerkt hast, dürften übereinandergelegte Bezugssysteme bei physikalischen Veranschaulichungen auch nicht gerade der Klassiker sein. ;)

Im zweidimensionalen geht es noch mit dem klassischen Minkowski-Diagramm, aber ich habe noch nie ein übereinandergelegtes 3D-Minkowski-Diagramm gesehen. Ich hatte hier mal eins eingestellt für eine Bewegun in x-Richtung:

Original anzeigen (0,2 MB)

Man sieht hier das x' und ct' eingedreht sind, wie man es vom 2D kennt und y auf y' abgebildet wird, das heißt es findet keine Längenkontraktion in y-Richtung statt bei einer Bewegung in x-Richtung. WEnn jetzt aber noch eine relativistische Bewegung in y-Richtung dazukommt wird es kompliziert.

Libertin schrieb:Ich denke aber, daß Deine Erläuterungen und Bilder hierzu es für viele Mitleser nun wesentlich verständlicher machen konnten. :Y:

Ich hoffe :-)

skagerak schrieb:Danke @mojorisin :)

Gern geschehen.

@nocheinPoet

nocheinPoet schrieb:Wie kann das sein, in welche Richtung dreht man sich, und bei einer Rotation müssten doch Zentripedalkräfte auftreten.

Ich kann dir keine direkte Antort darauf geben, aber habe jetzt Literatur gefunden die deinem PRoblem ähnlich sind:

Wikipedia: Thomas precession

For a given inertial frame, if a second frame is Lorentz-boosted relative to it, and a third boosted relative to the second, but non-colinear with the first boost, then the Lorentz transformation between the first and third frames involves a combined boost and rotation, known as the "Wigner rotation" or "Thomas rotation".

Llewellyn Thomas hat schon vor knapp hundert Jahren (1926) einen Effekt beschrieben der darauf beruht.

Im Artikel zur Wigner Rotation liest sich dann:

If a sequence of non-collinear boosts returns an object to its initial velocity, then the sequence of Wigner rotations can combine to produce a net rotation called the Thomas precession....
There are still ongoing discussions about the correct form of equations for the Thomas rotation in different reference systems with contradicting results.[4] Goldstein:[5]

"The spatial rotation resulting from the successive application of two non-collinear Lorentz transformations have been declared every bit as paradoxical as the more frequently discussed apparent violations of common sense, such as the twin paradox."

Einstein's principle of velocity reciprocity (EPVR) reads:[6]

"We postulate that the relation between the coordinates of the two systems is linear. Then the inverse transformation is also linear and the complete non-preference of the one or the other system demands that the transformation shall be identical with the original one, except for a change of v to −v"

With less careful interpretation, the EPVR is seemingly violated in some models.[7] There is, of course, no true paradox present.

@mojorisin

Cool, wenn ich etwas mehr Zeit habe, komme ich darauf zurück, habe was für Dich gefunden:




https://www.gbeyerle.de/twr/

@nocheinPoet

Nice. Das liefert ein netten Abschluss zu dieser Fragestellung.

Ich versuchs nochmal zu verlinken:


https://www.gbeyerle.de/twr/

@mojorisin

Moin, also so abgeschlossen habe ich es noch nicht, werde dazu noch einen eigenen Thread aufmachen, die Tage, denn das ist echt spannend.

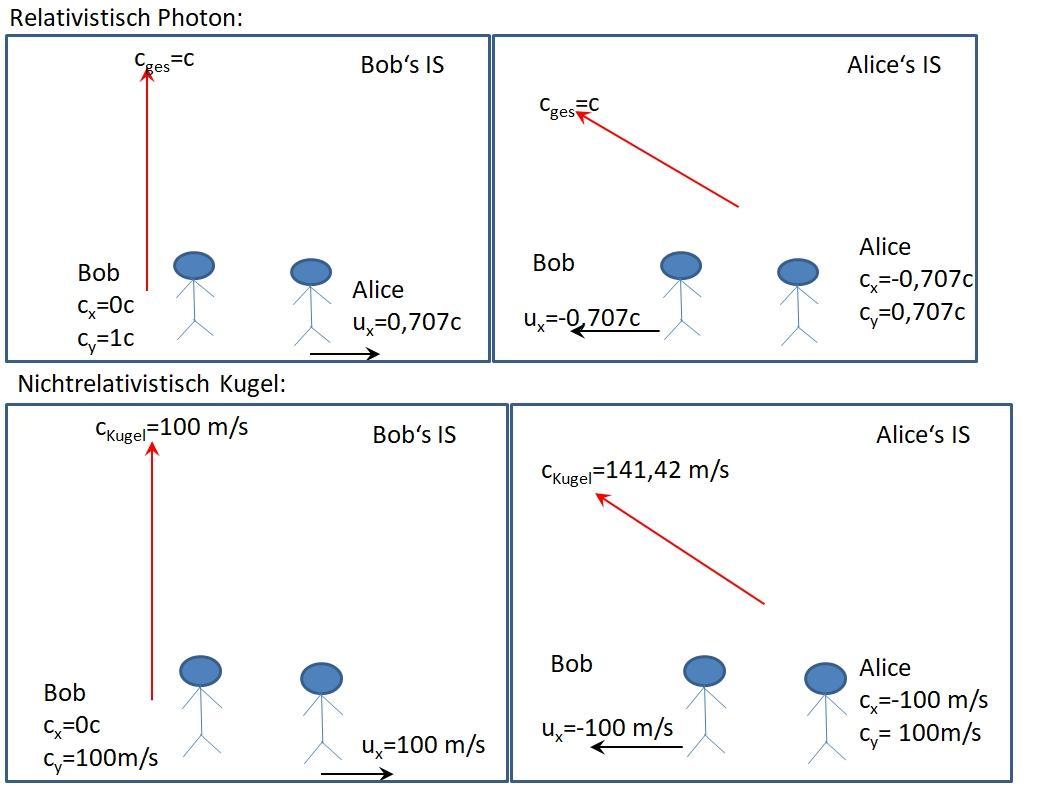
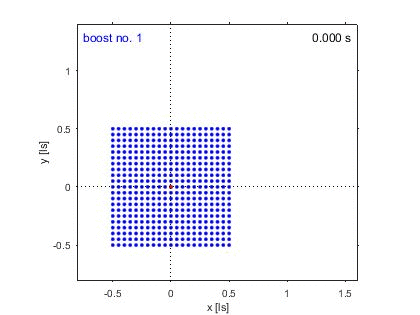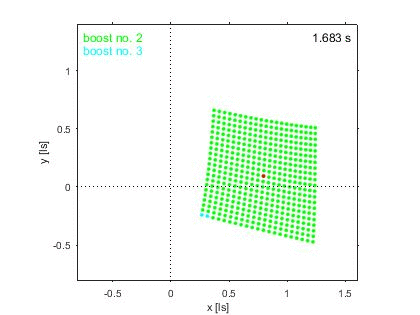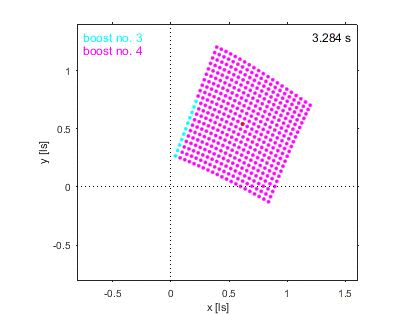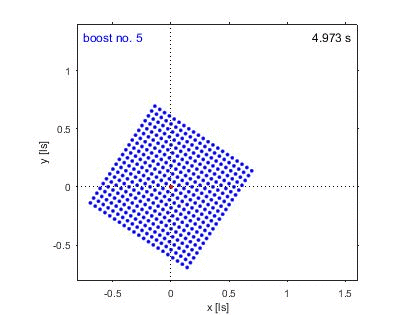
Ich sehe es noch nicht als abgeschlossen, weil die Frage selber noch nicht ganz direkt beantwortet ist, der Weg ist klar, gibt wo eine Rotation. Aber die Details fehlen noch, ich hatte ja durch vier Beschleunigungen die Richtung des Photons auf der y-Achse um 180 Grad gedreht. Die Frage ist nun, geht es so und bedeutet es, die beschleunigte Rakete hat sich dabei dann wirklich um 180 Grad im Raum gedreht? Wie verteilt sich die dann diese Rotation auf die einzelnen Beschleunigungen?

Wie gesagt, toll was Du da gefunden hast, super Sache, Hut ab, danke Dir. Wird mein Verständnis der SRT wieder noch mal erweitern, ist wohl nun echt schon tief im Eingemachten und die etwas höhere Schule der SRT.

Dennoch bleiben die genanten Fragen und ein paar mehr noch offen. Man könnte zum Beispiel einen relativistischen Raytracer nehmen, reicht auch fiktiv, real wäre natürlich der Hammer, und schauen wie es wohl so aus den Fenstern nach vorne und hinten und zu den Seiten in einer Rakete ausschaut, die so vier mal beschleunigt wird. Die hat zuerst die Sonne hinter und die Erde vor sich.

Wie schaut es nach den vier Beschleunigungen aus, schaut man dann nach vorne aus der Rakete und sieht nun aber die Sonne und die Erde hinter sich? Man ist nur rotiert und fliegt mit dem Hintern voran?

Also wie gesagt, ich sage mal, der Weg ist nun bekannt, hat was mit Rotation im Raum zu tun, aber es bleiben doch noch ein paar Detailfragen offen, und das dann zu rechnen ist noch mal eine Schippe oben drauf.

@mojorisin

Herr Senf hat mir noch einen guten Link gegeben:

http://www-e.uni-magdeburg.de/mertens/teaching/seminar/themen/relativistic_combination_velocities.pdf

Ich brauche da etwas länger für, aber eventuell rockt es Dich ja, gibt sogar Alice und Bob ... :D

@mojorisin

Cool, dank Senf haben wir da doch mal wirklich die Gleichungen für den Winkel und den ganzen Kram, eben mal so überlesen das Dokument, damit sollte man doch über den Winter kommen, ... :D

@mojorisin

Noch was, hier Seite 31:

https://kabinett.homepage.t-online.de/papers/so13/lorentz.pdf (Archiv-Version vom 01.03.2021)