mojorisin schrieb:Sind alle Fragen mit der Beantwortung der oberen Frage geklärt?
mojorisin schrieb:Sind alle Fragen mit der Beantwortung der oberen Frage geklärt?
Ja, danke. Ich komme auf die gleichen Ergebnisse wie du.
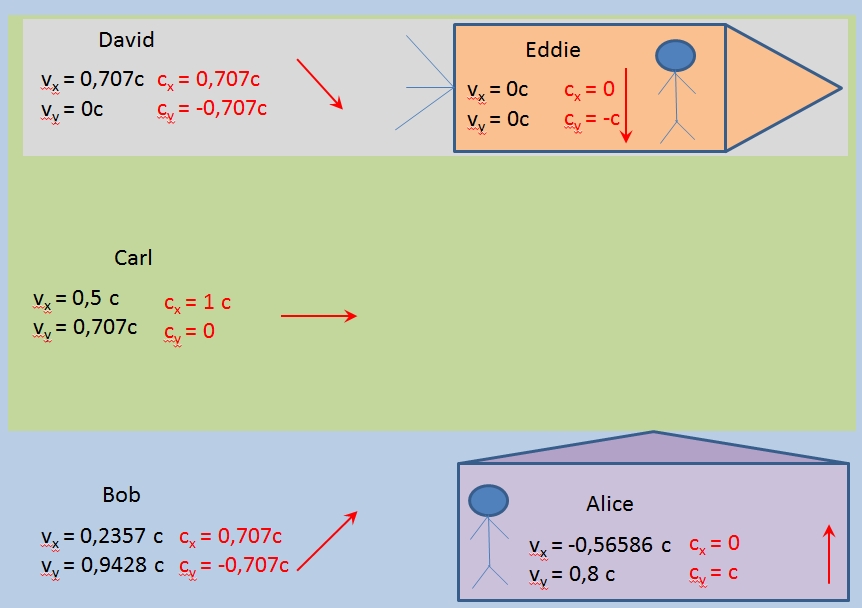
Carl aus Sicht von Bob:
u_y'=\frac {\sqrt {1- \left ( \frac {v^2} {c^2} \right )}u_y} {1- \frac {v} {c^2}u_x}=\frac {\sqrt {1- \left ( \frac {0{,}707c} {1c} \right )^2}\cdot0{,}707c} {1- \frac {0{,}707c} {1c^2}\cdot0c}=0{,}5c
David aus Sicht von Bob:
u_y'=\frac {\sqrt {1- \left ( \frac {v^2} {c^2} \right )}u_y} {1- \frac {v} {c^2}u_x}=\frac {\sqrt {1- \left ( \frac {0{,}707c} {1c} \right )^2}\cdot0{,}99c} {1- \frac {0{,}707c} {1c^2}\cdot0c}=0{,}7c
Alice aus Sicht von Bob:
u_x'=\frac {u_x-v}{1- \frac{v}{c^2}u_x}=\frac {0c-0{,}707c}{1- \frac{0{,}707c}{1c^2}\cdot0c}=-0{,}707c
Eine frage hätte ich da in Bezug auf Carl dennoch. Wenn Carl sich wie in dem Beispiel aus Sicht von Alice mit 0,707c auf der y-Achse bewegt, Carl nun zusätzlich auf der x-Achse beschleunigt, so dass er aus Sicht von Alice u
x=0,7c erreicht, welche Geschwindigkeiten ergeben sich dann aus Sicht von Bob?
Ich komme da auf folgende Beträge:
Carl aus Sicht von Bob:
u_y'=\frac {\sqrt {1- \left ( \frac {v^2} {c^2} \right )}u_y} {1- \frac {v} {c^2}u_x}=\frac {\sqrt {1- \left ( \frac {0{,}707c} {1c} \right )^2}\cdot0{,}707c} {1- \frac {0{,}707c} {1c^2}\cdot0{,}7c}=0{,}99c
u_x'=\frac {u_x-v}{1- \frac{v}{c^2}u_x}=\frac {0{,}7c-0{,}707c}{1- \frac{0{,}707c}{1c^2}\cdot0{,}7c}=-0{,}014c
Stimmst du dem zu?