mojorisin
Diskussionsleiter

Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen

dabei seit 2011
Profil anzeigen
Private Nachricht
Link kopieren
Lesezeichen setzen
Woher kam das Problem der Ultraviolettkatastrophe?
16.12.2018 um 18:11Im Thread "Jahrestage der Wissenschaft" kam die Frage auf "Warum es Probleme gab zu erklären warum ein Ofen nicht glüht wenn er kalt ist".
Der Aufwurf kam dazu von @Peter0167 in diesem Thread: Jahrestage der Wissenschaft (Seite 9) (Beitrag von Peter0167). Da das Problem recht interessant ist und einen Einstieg in die Quantenmachnik gibt will ich die Antwort dazu gerne hier diskutieren.
Nun um das Problem zu verstehen woher die Ultraviolettkatastrophe kommt muss man verstehen wie das Rayleigh-Jeans-Gesetzt hergeleitet wurde. Ich will dazu die dahinterstehenede Mathematik eher grafisch veranschaulichen als mit Formeln, in der Hoffnung das dies das Verständnis erleichtert.
Das Rayleight-Jeans wird folgendermaßen begründet:
Wikipedia: Plancksches Strahlungsgesetz#Herleitung und Historie
Was bedeutet das? NUn folgende 1D Grafik soll das Veranschaulichen:
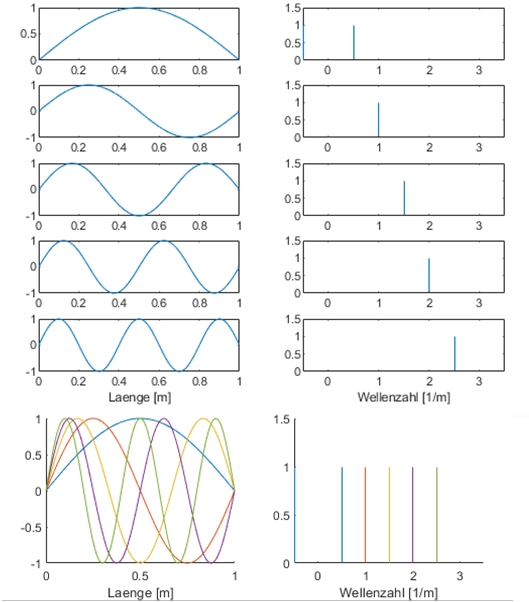
Auf der linken Seite sehen wir einen 1D Hohlraum in dem die ersten fünf möglichen Moden eingezeichnet sind. Auf der rechten Seite sehen wir das dazugehörige Spektrum der einzelnen Moden. Die erste Mode ist eine Halbwelle die sich über einen Meter erstreckt. Eine längere Mode passt nicht in den Hohlraum daher ist das die tiefstmögliche Frequenz. Im Spektrum hat man daher einen Peak bei 0.5 \frac{1}{m} . Die nächste Mode ist ein Ganze Welle mit einem Peak bei 1 \frac{1}{m} . Hier sind die ersten fünf Moden aufgezeichnet tatsächlich passen aber unendlich viele Moden in diesen Hohlraum.
Im untersten Diagramm sind man nun die Überlagerung der ersten fünf Moden wie sie sich im Kasten ausbreiten (links) und die dazugehörige spektrale Verteilung.
Im untersten rechten DIagramm sehgen wir nun die sogenannte "Zustandsdichte" der ersten fünf Moden. Das Wort bedeutet nicht mehr als das man damit aussagen kann wie hoch die Wahrscheinlichkeit ist eine Mode einer bestimmten WEllenzahl zu finden. Die Wahrscheinlichkeit ist 0 eine Welle mit der Frequenz 1.25 \frac{1}{m} zu finden aber sie ist z.B. = 1 eine Welle mit der WEllenzahl 1 \frac{1}{m} zu finden.
In diesem eindimensionalen Fall haben also alle Wellenzahlen die entweder halbzahlig oder ganzzahlig sind eine 100% Besetzungswahrscheinlichkeit.
Wichtig hier: Das alles hat bis hierhin noch nichts mit Quantisierung zu tun.
WEiters im Wiki-Link:
1. gleich viel Energie abbekommt nämlich k_B \cdot T, und
2. diese Energie wäre kontinuierlich
Punkt 2. bedeutet jede Mode könnte beliebig kleine Portionen an Energie tragen.
Wollen wir nun die Gesamtenergie berchnen würden wir ganz einfach die Energien der einzelnen Moden aufaddieren. Da es aber unendlich viele Moden gibt und jede den gleichen Energieanteil besitzt erhält man daher das in diesem Hohlraumresonator unendlich viel Energie drinne sein muss. Man nennt dies die sogenannte Ultraviolett-Katastrophe.
Hier will ich an dieser Stelle mal stoppen und Fraghen diskutieren falls welche da sind.
Der Aufwurf kam dazu von @Peter0167 in diesem Thread: Jahrestage der Wissenschaft (Seite 9) (Beitrag von Peter0167). Da das Problem recht interessant ist und einen Einstieg in die Quantenmachnik gibt will ich die Antwort dazu gerne hier diskutieren.
Nun um das Problem zu verstehen woher die Ultraviolettkatastrophe kommt muss man verstehen wie das Rayleigh-Jeans-Gesetzt hergeleitet wurde. Ich will dazu die dahinterstehenede Mathematik eher grafisch veranschaulichen als mit Formeln, in der Hoffnung das dies das Verständnis erleichtert.
Das Rayleight-Jeans wird folgendermaßen begründet:
Man betrachte als vereinfachtes Beispiel einen würfelförmigen Hohlraum der Seitenlänge L und des Volumens V, der elektromagnetische Hohlraumstrahlung im thermischen Gleichgewicht enthält. Im Gleichgewicht können sich nur stehende Wellen ausbilden; die erlaubten Wellen können in beliebige Richtungen laufen, müssen dabei jedoch die Bedingung erfüllen, dass zwischen zwei gegenüberliegende Hohlraumflächen jeweils eine ganzzahlige Anzahl von Halbwellen passt. Das hat folgenden Grund: Da die elektromagnetischen Wellen innerhalb der Wände des Hohlraums nicht existieren können, ist dort die elektrische und magnetische Feldstärke null. Damit müssen sich die Knotenpunkte der Wellen an den Oberflächen der Innenwände befinden. Es sind also nur bestimmte diskrete Schwingungszustände erlaubt; die gesamte Hohlraumstrahlung setzt sich aus diesen stehenden Wellen zusammen.
Wikipedia: Plancksches Strahlungsgesetz#Herleitung und Historie
Was bedeutet das? NUn folgende 1D Grafik soll das Veranschaulichen:

Auf der linken Seite sehen wir einen 1D Hohlraum in dem die ersten fünf möglichen Moden eingezeichnet sind. Auf der rechten Seite sehen wir das dazugehörige Spektrum der einzelnen Moden. Die erste Mode ist eine Halbwelle die sich über einen Meter erstreckt. Eine längere Mode passt nicht in den Hohlraum daher ist das die tiefstmögliche Frequenz. Im Spektrum hat man daher einen Peak bei 0.5 \frac{1}{m} . Die nächste Mode ist ein Ganze Welle mit einem Peak bei 1 \frac{1}{m} . Hier sind die ersten fünf Moden aufgezeichnet tatsächlich passen aber unendlich viele Moden in diesen Hohlraum.
Im untersten Diagramm sind man nun die Überlagerung der ersten fünf Moden wie sie sich im Kasten ausbreiten (links) und die dazugehörige spektrale Verteilung.
Im untersten rechten DIagramm sehgen wir nun die sogenannte "Zustandsdichte" der ersten fünf Moden. Das Wort bedeutet nicht mehr als das man damit aussagen kann wie hoch die Wahrscheinlichkeit ist eine Mode einer bestimmten WEllenzahl zu finden. Die Wahrscheinlichkeit ist 0 eine Welle mit der Frequenz 1.25 \frac{1}{m} zu finden aber sie ist z.B. = 1 eine Welle mit der WEllenzahl 1 \frac{1}{m} zu finden.
In diesem eindimensionalen Fall haben also alle Wellenzahlen die entweder halbzahlig oder ganzzahlig sind eine 100% Besetzungswahrscheinlichkeit.
Wichtig hier: Das alles hat bis hierhin noch nichts mit Quantisierung zu tun.
WEiters im Wiki-Link:
Wenn alle Oszillatoren im thermischen Gleichgewicht bei der Temperatur T schwingen, dann wäre nach dem Gleichverteilungssatz der klassischen Thermodynamik zu erwarten, dass jeder dieser Oszillatoren im Mittel die kinetische Energie kT/2 und die potentielle Energie kT/2, also insgesamt die Energie kT trägt.Das heißt die Energie einer jeden Schwingung ergibt sich aus k_B \cdot T wobei kB die Boltzmann Konstante ist. Das bedeutet das jede Mode
1. gleich viel Energie abbekommt nämlich k_B \cdot T, und
2. diese Energie wäre kontinuierlich
Punkt 2. bedeutet jede Mode könnte beliebig kleine Portionen an Energie tragen.
Wollen wir nun die Gesamtenergie berchnen würden wir ganz einfach die Energien der einzelnen Moden aufaddieren. Da es aber unendlich viele Moden gibt und jede den gleichen Energieanteil besitzt erhält man daher das in diesem Hohlraumresonator unendlich viel Energie drinne sein muss. Man nennt dies die sogenannte Ultraviolett-Katastrophe.
Hier will ich an dieser Stelle mal stoppen und Fraghen diskutieren falls welche da sind.




