@TangMi leichter gesagt, als getan.
Aber ich habe dies in meinem Eingangsposting berücksichtigt, ich zitiere mich mal selbst.
Albert Einstein meinte, der Mond würde nicht verschwinden, nur weil niemand hinschauen würde. Das stimmt so, aber das Problem ist, dass er nicht erkannt hat, dass seine Gleichung nicht vollständig ist. Denn der Mond würde nur dann verschwinden, wenn er mit nichts, was in der menschlichen Realität existiert interagiert, also mit nichts, dessen Zustand auf den Einfluss eines Mondes hinweisen würde. Diesen Zustand können wir also nicht herbeiführen, da die Frage nach der Existenz des Mondes bereits geklärt ist, somit gibt es keine Überprüfungsmöglichkeit für diese Behauptung, es sei denn man könnte beim Doppelspaltexperiment die Wellenmuster durch eine Untersuchung der Aufprallfläche im Nachhinein verschwinden lassen, in dem Moment wo man das Teilchen entdeckt.
Als erstes führe ich eine Theorie an, die offenbar von Albert Einstein stammt, deren Gleichung nicht korrekt zu sein scheint, um an das Thema heranzuführen. Das ist ein Beispiel, wo ich ansetze um die Zusammenhänge leichter begreifbar zu machen. Zudem versuche ich eine Voraussage zu machen. Das ist um genau zu sein, sogar eine weit bessere Ausgangslage als die der Stringtheorie.
Aber es ist nicht einfach sich eine Situation vorzustellen, in der eine praktische Überprüfung realisierbar ist.
Denn, wenn man ein Teilchen in Superposition dazu bringt mit der Umwelt zu interagieren, verliert es ja dann, wenn es in der logischen Folge dadurch beobachtet werden kann, meist seine Superposition. Deshalb muss man es dazu bringen, mit der Umwelt auf eine Art zu interagieren, die zum Zeitpunkt der Interaktion von der Realität isoliert ist.
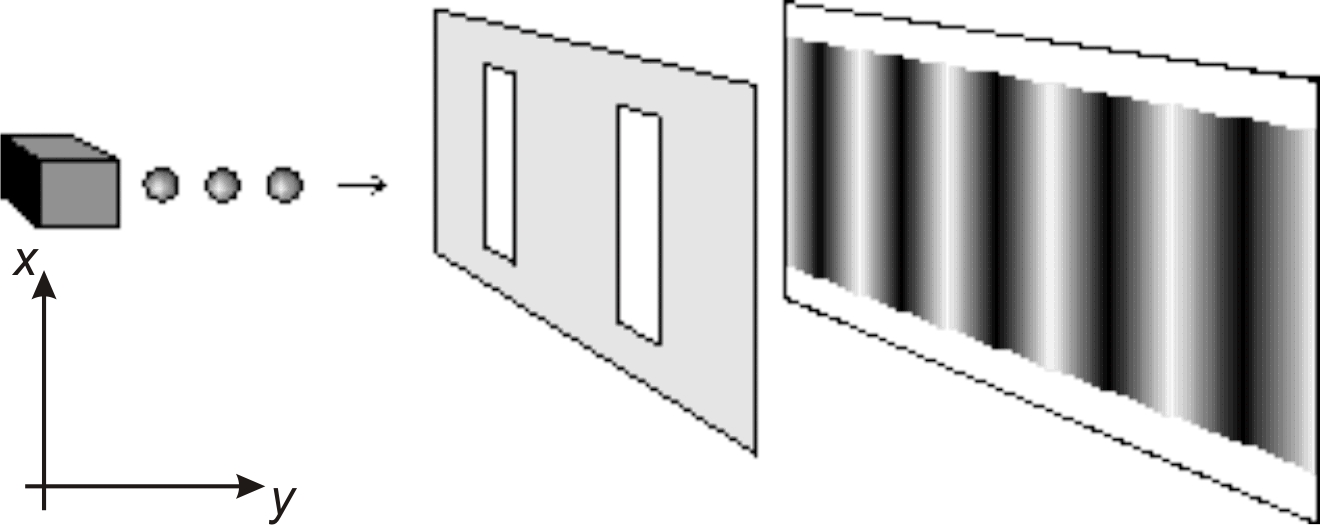
Nehmen wir an, wir schiessen ein Atom auf einen Doppelspalt und erhalten die Interfernzkurven, so sind diese Folge des Aufpralls des sich in lokaler Superposition (wir wissen nicht wo es ist) befindenden Atoms. Wir sehen die Auswirkungen, die die Eigenschaften des Atoms auf seine Umwelt haben deshalb auch an allen Orten, an denen es sich befinden könnte oder müsste, und das genau deshalb, weil die Eigenschaften des Atoms bekannt sind.
Als logische Folge muss der Effekt, den das Atom auf seine Umwelt in lokaler Superposition hat an seine lokale Superposition gebunden sein, denn man kann Atome sonst nirgendwo in Form von Wellen beobachten (so weit mir bekannt).
Wenn die Interferenzkurven also vom Zustand des Atoms abhängig sind, und es stimmt, dass sich das Atom momentan in Wirklichkeit an keinem dieser Orte befindet, wo seine Superposition Spuren hinterlässt, so müssten seine Auswirkungen genau so wenig dort existieren, wo wir sie sehen. Oder zu mindest besteht die Möglichkeit dazu, dass es so sein könnte.
Wenn man nun dieses Atom sucht, und angenommen wir finden es, können eindeutig beweisen, dass es sich um genau das Atom handelt, welches den Doppelspalt passiert hat, somit besteht die Möglichkeit, dass nicht nur das Atom seine lokale Superposition verliert, sondern auch seine in diesem Zustand hinterlassenen Spuren verschwinden.
Die Frage ist jetzt nur, wie man so etwas anstellen könnte, denn dann würde ich sicher mit einem Schlag eine wesentlich andere Resonanz auf die Theorie erhalten.
Aber gut, dass Du das genau wie ich siehst was die Glaubwürdigkeit von Theorien betrifft.