Das wird in dem Veritasium-Video das ich als letztes geposted habe ganz gut erklärt. Das Prinzip ist die Drehimpulserhaltung. Wenn das System still steht, dann ist die Schwerkraft genügend groß, um das System in Drehung zu versetzen. Wenn sich das System aber in Rotation befindet kann man es nicht mehr einfach drehen. Das liegt daran, dass dazu die Drehung dazu komplett gestoppt werden muss, bzw. in eine andere Richtung überführt werden muss, was einen sehr hohen Aufwand bedeutet. Aber wie gesagt, schau dir das Video an, dann solltest du die Grundlegenden Ideen dahinter verstehen
:)Allerdings ist der tatsächliche Vorgang noch etwas komplizierter als dort erklärt: Jeder starre Körper hat drei besondere Achsen, die sogenannten Hauptträgheitsachsen. Eine stabile Rotation ist nur um diese speziellen Achsen möglich, alles andere ist instabil. Dazu kommt, dass nur die größte und die kleinste Hauptträgheitsachse wirklich stabil sind, die mittlere ist labil.
Dazu kannst du einen einfachen versuch machen. Nimm z.B. ein Kartenspiel (in der Schachtel) und wirf es mit Drehung aus dem Handgelenk in die Luft. Je nachdem um welche Achse es sich dreht bekommst du eine "saubere" Drehung, oder das Kartenspiel fängt an in der Luft herumzueiern. Hier mal eine kleine Illustration dazu:
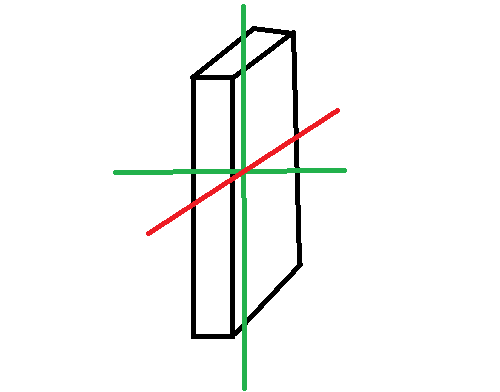
Drehung um die grünen Achsen sind stabil, Drehung um die rote ist labil. Woran liegt das? Wenn ein Körper sich dreht dann wirken auf alle Teile Zentrifugalkräfte. Aber im Allgemeinen sind diese Zentrifugalkräfte nicht symmetrisch verteilt. Im Endeffekt hast du also durch die Drehung ein Drehmoment auf den Körper wirken, der ihn verkippt (sogenannte Deviationsmomente). Und da sich der Körper ständig in eine andere Richtung dreht, sieht man in herumeiern.
Die Hauptträgheitsachsen sind besondere Symmetrieachsen, bei denen die Kräfte sich aufheben. Und davon gibt es wie gesagt immer drei Stück.
Was passiert wenn eine winzige Störung den Körper, der sich gerade um eine Hauptträgheitsachse dreht, etwas aus der Lage bringt? Nun, bei zwei der Trägheitsachsen führen die entstehenden Deviationsmomente dazu, dass der Körper wieder zurück auf die Trägheitsachse gerückt wird. Deswegen ist die Drehung dann stabil. Bei der dritten Trägheitsachse wirkt das Drehmoment von der Hauptträgheitsachse weg, die Abweichung wird also verstärkt.
Das wichtige ist jetzt, dass ein Körper immer versucht, sich so zu drehen, dass seine Hauptträgheitsachsen genau mit dem Drehimpuls ausgerichtet ist. D.h. wenn der Körper falsch liegt, dann entsteht das "Eiern", oder in Fachsprache "Nutation", und zwar so lange, bis das Drehmoment verschwindet. Ob das passiert kommt immer auf das System an, wenn genügend Reibung vorhanden ist um die Nutationsbewegung zu dämpfen kommt der Körper irgendwann mit seiner HTA auf dem Drehmoment (das ja unveränderlich ist) zum liegen.
Was passiert jetzt, wenn ein Körper, der sich sauber dreht, ein äußeres Drehmoment erfährt? Nun, wie du in dem Video gesehen hast verändert sich der Drehimpuls. Das bedeutet aber, dass der Körper nicht mehr um seine Hauptträgheitsachse rotiert. Er wird jetzt versuchen, dem Drehimpuls zu folgen, ein Effekt der eben durch die Deviationsmomente entsteht. Wenn der Körper sich schnell genug dreht, dann sind die Deviationsmomente groß genug, dass er schnell genug dem Drehmoment hinterhereilen kann. Wenn der Körper nicht mehr schnell genug dreht, dann wird er umfallen.
Den Effekt kannst du in deinem Video wunderbar an dem Versuch bei [56:40] sehen. Die "Scheibe" ist verzerrt, weil unterschiedliche Zentrifugalkräfte wirken.
Den Versuch den du jetzt angesprochen hast ([27:10]) kannst du damit ganz leicht auf diese Phänomene zurückführen. Würde die gesamte Platte kippen, dann ändert sich die Richtung des Körpers. Dies wäre aber nur möglich, wenn der Kreisel gerade parallel zur Tischkante steht. Dann kann die Platte kippen, ohne dass sich die Richtung des Drehmoments ändert. Da sich der Kreisel auf der Platte aber ständig dreht (Präzessionsbewegung) kann die Platte die meiste Zeit über nicht bewegt werden, ohne dass Deviationsmomente versuchen, den Körper zurück zu drehen.
Hier noch ein lustiges Video zu dem Thema:
https://www.youtube.com/watch?v=cRJv6z_bxQg






