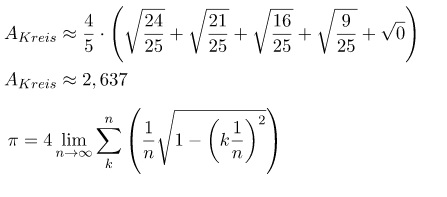Kann Pi plötzlich enden?

@AnGSt
Nehmen wir an, dass es eine sich immer wiederholende Zahlenfolge a = a_1, a_2, a_3 ... a_n gibt, so dass pi = 3.aaaaaaa.... gilt.

pi = 3 + 0.aaaaaa....
pi * 10^n = 3*10^n + a.aaaaa....
pi * 10^n - 1 = 3*10^n + a
pi = 3 + a / (10^n - 1)

Damit wäre pi nicht transzendent. Widerspruch.

Also kann pi nicht unendlich periodisch sein. Es können sich zwar Passagen wiederholen, aber es ist nicht periodisch.

@zaeld

Achso... :P

Bumbelbee schrieb:
Nicht die Annäherung an Pi ist Irrational sondern Pi selbst, darum gings.

Aus den Annäherungen wurde aber irgendwie gefolgert, daß Pi irrational sein muß. Hier die ursprüngliche Aussage (von der vorigen Seite):

"weil Pi, meines Wissens, zur Annäherung an ein Unendlicheck genutzt wird (Kreis) und da dieser bekanntlich über unendlich viele Ecken verfügt muss die Zahl auch unendlich lang sein."

Ich glaube die allgemeine Verwirrung liegt darin dass zwei unterschiedliche Annäherungen gemeint sind. Du sprichst von der Annäherung an Pi selbst und er Sprich von der Annäherung von Pi an einen "Punkt", sprich die Transzendenz von pi.

zaeld schrieb:Die Schlußfolgerung 'unendlich viele Ecken, deshalb muß Pi irrational sein' ist ganz einfach keine - zumindest fehlen dafür wesentliche Teile:

Verstehe nicht ganz weshalb man das so nicht sagen kann, das Verhältnis von Umfang zu Durchmesser kann einfach nicht absolut ermittelt werden da wir es mit einem Kreis bzw. Kreisbogen zutun haben.

zaeld schrieb:Ein rechtwinkliges Dreieck mit den beiden kurzen jeweiligen Seitenlängen 1 kann man auch durch viele schmale Rechtecke annähern, im Grenzfall unendlich viele. Nach dieser von mir kritisierten Schlußfolgerung müßte der Flächeninhalt logischerweise auch irrational sein, da ja unendlich viele Rechtecke verwendet wurden. Ist es aber nicht, der Flächeninhalt ist 1/2.

Die Anwendung eines "unendlichecks" auf eine Dreieck mit geraden Linien wäre auch irgendwie Sinnfrei wenn du mich fragst. :P

Sorry ,falls das hier schon mal geklärt wurde, ansonsten meine Frage:
Wie oft kann in der Zahlenfolge von PI die gleiche Ziffer (z.B. die 0)
hintereinander (maximal) vorkommen ?

@Bumbelbee

Bumbelbee schrieb:Ich glaube die allgemeine Verwirrung liegt darin dass zwei unterschiedliche Annäherungen gemeint sind. Du sprichst von der Annäherung an Pi selbst und er Sprich von der Annäherung von Pi an einen "Punkt", sprich die Transzendenz von pi.

Hm, ich wüßte nicht, wie man Pi an etwas annähern könnte, denn das ist ja eine feste Zahl. Was man annähern kann, ist der dargestellte Wert, der dem tatsächlichen Wert von Pi eben möglichst nahe kommen soll.

Vielleicht wiederhole ich mich ja, aber man kann doch aus dem Verfahren, einen Kreis in unendlich viele Rechtecke zu unterteilen, um daraus den Wert von Pi zu ermitteln, nicht einfach folgern, daß wegen der unendlichen Unterteilung Pi irrational ist. Da fehlt doch irgendein Gedankengang.

Bumbelbee schrieb:Verstehe nicht ganz weshalb man das so nicht sagen kann, das Verhältnis von Umfang zu Durchmesser kann einfach nicht absolut ermittelt werden da wir es mit einem Kreis bzw. Kreisbogen zutun haben.

Gut, und wie ist die logische Folgerung von Kreisbogen zu Irrationalität? Wodurch ist ausgeschlossen, daß Pi nicht doch eine rationale Zahl ist (abgesehen von den anderen existierenden Beweisen, daß Pi irrational ist)? Nur weil das ein Kreisbogen ist, wird doch Pi nicht automatisch irrational. Oder vielleicht doch, aber dann fehlt bisher die Erklärung dazu.

Bumbelbee schrieb:Die Anwendung eines "unendlichecks" auf eine Dreieck mit geraden Linien wäre auch irgendwie Sinnfrei wenn du mich fragst.

In welcher Hinsicht? Weil man für die Berechnung eines Dreiecks auch einfachere Methoden hat oder weil ein Dreieck nun mal kein Kreis ist und nicht aus unendlich vielen Ecken besteht?

Wenn letzteres: Damit ist gemeint, daß du z.B. ein rechtwinkliges Dreieck genauso wie einen Kreis durch viele kleine Rechtecke annähern kannst. Man hat dann z.B bei einem rechtwinkligen Dreieck die beiden kurzen Seiten wie bisher, und die lange Seite wird dann eine Treppe mit vielen Ecken. Bei unendlich kleinen Rechtecken hat man dann undlich viele Treppenstufen auf der langen Seite und damit auch wieder ein Unendlicheck, allerdings unsymmetrisch..

Also so, ich hoffe, das wird einigermaßen dargestellt:

***
***
***---
***---
***---***
***---***
***---***---
***---***---

Das soll ein Dreieck mit der Spitze oben links sein. * und - bilden die Rechtecke zur Annäherung des Dreiecks. Das wären jetzt 3 Ecken nur in der schrägen Gerade, plus 2 Ecken unten links und rechts. Und so wird dann ein Unendlicheck draus, indem aus den 3 Kanten unendlich viele werden.

Z.

@zaeld

zaeld schrieb:ich wüßte nicht, wie man Pi an etwas annähern könnte, denn das ist ja eine feste Zahl.

Ich auch nicht. Wo habe ich das geschrieben? Pi selbst beschreibt einen Annäherung. Was verstehst du unter "feste Zahl"? Ist das irgendwo definiert?

zaeld schrieb:Vielleicht wiederhole ich mich ja, aber man kann doch aus dem Verfahren, einen Kreis in unendlich viele Rechtecke zu unterteilen, um daraus den Wert von Pi zu ermitteln, nicht einfach folgern, daß wegen der unendlichen Unterteilung Pi irrational ist. Da fehlt doch irgendein Gedankengang.

Naja es ist sicher kein Beweis, man müsste schon wissen wie die Unterteilung genau zustande kommt.

Jedoch sehe ich nirgends das jemand Behauptet hat die Zahl müsse auch irrational sein nur deswegen (weil die Anzahl Ecken unendlich sind), es ging dabei alleine um die Unendlichkeit von pi. In dieser Hinsicht ist die Schlussfolgerung doch legitim?

zaeld schrieb:In welcher Hinsicht? Weil man für die Berechnung eines Dreiecks auch einfachere Methoden hat oder weil ein Dreieck nun mal kein Kreis ist und nicht aus unendlich vielen Ecken besteht?

Aus welchem Grund sollte man bei einem Dreieck dessen Inhalt man exakt bestimmen kann mit einer Annäherung arbeiten? Das ergibt keinen Sinn. Bei einem Kreis hingegen schon. Weshalb genau das so ist kannst du ja unter Infinitesimalrechnung nachschlagen (vermutlich weisst du das aber schon) .

zaeld schrieb:Eine nicht zufriedenstellende Antwort, weil die Folgerung, daß Pi unendlich viele Stellen zur Folge hat, nicht logisch hergleitet wird, sondern nur einfach hinbehauptet wird.

Ein logisch-formaler Beweis der Irrationalität von Pi - die dann unmittelbar auch die Folgerung nach sich zieht, dass die Anzahl der Nachkommastellen von Pi unendlich ist - würde, Pi mal Daumen, ja auch ca. 100% der Userschaft hier völlig überfordern...

skmo schrieb:Die Antwort von @unecht ist durchaus zufriedenstellend, es kann ja keine rationale Zahl herauskommen, wenn man nur eine Annäherung verwendet indem man eckig etwas rundes beschreiben will ! Jede Integralrechnung liefert die gleiche nicht zufriedenstellende Genauigkeit.
Kann ich etwas nicht genau beschreiben, muß mein annäherndes Ergebnis immer unendlich viele Kommastellen haben.

Ja, komisch... Die Fläche unter dem ersten Sinus-Hügel* beträgt zufälligerweise gerade und ziemlich genau 1, also sogar eine Ganze Zahl...

*also die rote Fläche hier:

Bumbelbee schrieb:Die Herleitung von Pi an sich bedingt ja schon eine unendliche Zahlenfolge.

Pi wird nicht hergeleitet, sondern definiert... und zwar als Verhältnis von Umfang eines Kreises zu seinem Durchmesser.

zaeld schrieb:Pi kann nur irrational sein weil sie eine Annäherung an das Verhältnis von Umfang zu Durchmesser ist und keine Absolute Zahl.

Nope. Betrachte bspw.:

Folge f_n=1/n

Sämtliche Folgenglieder sind rational, sind eine Annäherung an die 0 (ganze Zahl), die gleichzeitig auch der Grenzwert der Folge ist, wenn n gg. unendlich strebt.

Auch "Annäherung" scheidet also als jedwedes Argument für Irrationalität aus...

skmo schrieb:Das erste Bild erklärt auch gleichzeitig die UNGENAUIGKEIT der Integralrechnung danke! ;)

Hm... wie es wohl kommt, dass beim Riemann-Integral Grenzwert von Ober- und Untersumme exakt übereinstimmen, obwohl die Integralrechnung doch so ungenau ist...? :ask:

skmo schrieb:Wurzel aus 2, und diese Zahl hat wieviele Stellen nach dem Komma......? ;)

Ich habe mit dem Taschenrechner nachgerechnet... Es sind 9! :)

zaeld schrieb:Da wie gesagt die Rechtecke, die die Fläche unter der Kurve annähern sollen, bei der Integralrechnung die Breite 0 haben, wird die Fläche EXAKT nachgebildet, und zwar mit unendlich vielen Rechtecken.

Das ist genaugenommen nicht ganz korrekt. Ihre Breite ist nicht exakt Null, sondern lediglich infinitesimal ("unendlich klein")... Schönes Beispiel ist der Ausdruck:



Nun bilden wir den Grenzwert ("machen n unendlich groß")...



Und an dieser Stelle vllt. mal so eine kleine...

...Quizfrage in die "Experten"runde hier: Was kommt raus?! :ask:

Man könnte ja bspw. argumentieren (lol...), der Ausdruck in der Klammer sei exakt 1, wenn n unendlich groß wird. Denn im zweiten Summanden wird 1 durch unendlich geteilt, das sei eben 0, weshalb man in der Summe dann 1 erhält. Und '1 hoch irgendwas' bleibt 1. Selbst wenn man 1 unendlich oft mit 1 multipliziert, kommt ja immer noch 1 heraus. Also ist dann das Gesamtergebnis des obigen Ausdrucks 1.

Andererseits könnte man argumentieren (lol...), dass der Ausdruck in der Klammer eben nicht exakt 1 sei, sondern immer noch ein ganz klitzeklitzeklitze...kleines bisschen größer als 1. Und wenn man diesen Wert unendlich oft mit sich selbst multiplizieren würde, ginge auch das Ergebnis gegen unendlich.
(Man kann bspw. mal 1.001 in den Taschenrechner tippen und immer wieder mit 1.001 multiplizieren... dauert zwar ein Weilchen, aber der Wert wird immer größer und geht natürlich gegen unendlich, wenn man die Multiplikation unendlich oft wiederholt, klar. Und das klappt mit jedem beliebigen Wert größer 1, also bspw. 1.000000001, 1.000000000000000000000000001 oder 1.0000000000000000000000000000000000000000001 usf.)

Also...? :)

Bumbelbee schrieb:Pi selbst beschreibt einen Annäherung. Was verstehst du unter "feste Zahl"? Ist das irgendwo definiert?

Ja, Pi ist wie gesagt definiert als "Umfang geteilt durch Durchmesser eines Kreises". Das ist eine einzige feste Zahl. Da diese Zahl unendlich viele Stellen hinter dem Komma hat, schreibt man diese Zahl nicht aus, sondern nennt sie der Einfachheit halber "Pi".

Eine Zahl beschreibt keine Annäherung. Man kann sich bei der Berechnung des Wertes von Pi dem exakten Wert jedoch annähern. Zum Beispiel mit der von dir genannten Formel. Die hat aber Pi als Ergebnis, da wird Pi nicht verwendet.

Bumbelbee schrieb:Naja es ist sicher kein Beweis, man müsste schon wissen wie die Unterteilung genau zustande kommt.

Da man selber unterteilt, weiß man das ja. Allerdings kommt wegen der unendlichen Unterteilung nicht unbedingt eine irrationale Zahl heraus.

Bumbelbee schrieb:Jedoch sehe ich nirgends das jemand Behauptet hat die Zahl müsse auch irrational sein nur deswegen (weil die Anzahl Ecken unendlich sind), es ging dabei alleine um die Unendlichkeit von pi. In dieser Hinsicht ist die Schlussfolgerung doch legitim?

Wie lautet die Schlußfolgerung denn nun? "Weil man für die Berechnung von Pi ein Unendlicheck konstruiert, muß Pi irrational sein"?

Bumbelbee schrieb:Aus welchem Grund sollte man bei einem Dreieck dessen Inhalt man exakt bestimmen kann mit einer Annäherung arbeiten?

Um sich klar zu machen, daß eine Unterteilung in unendlich viele Rechtecke nicht zwingend zu einem irrationalen Ergebnis führt:

Nimm ein Koordinatensystem und zeichne im gleichen Abstand "r" von 0 einen Punkt auf die x-Achse und einen auf die y-Achse.

^
|
|
A
|
|
|
|
---------------B---->

Erster Versuch:

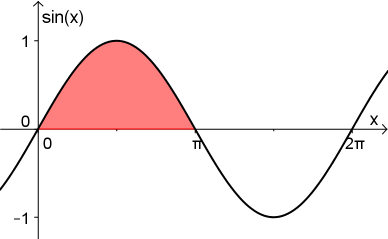
Verbinde A und B mit einem Kreisbogen, sodaß ein Viertelkreis entsteht.

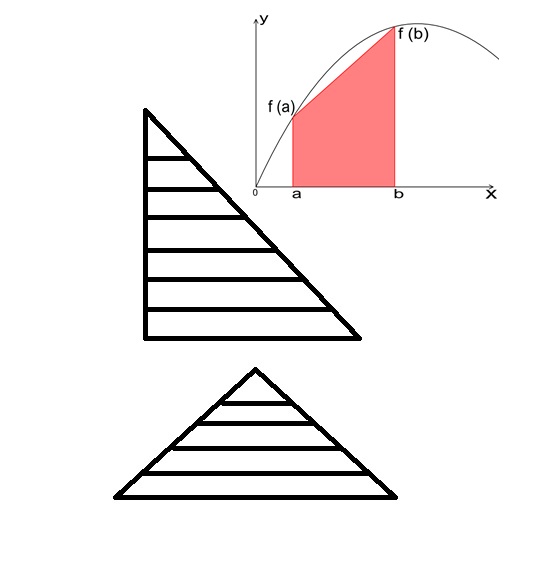
Berechne den Flächeninhalt unter dieser Kurve in Abhängigkeit von "r", indem unendlich viele Rechtecke in den Viertelkreis gelegt werden und die Summe darüber gebildet wird.

Als Ergebnis erhält man c * r^2, wobei eine c eine Konstante ist, und zwar Pi/4. c ist eine irrationale Zahl.

Zweiter Versuch:

Verbinde A und B mit einer Geraden, sodaß ein Dreieck entsteht.

Berechne den Flächeninhalt unter dieser Kurve in Abhängigkeit von "r", indem unendlich viele Rechtecke in das Dreieck gelegt werden und die Summe darüber gebildet wird.

Als Ergebnis erhält man c * r^2, wobei c wiederum eine Konstante ist, und zwar diesmal 1/2. c ist eine rationale Zahl.

Mit genau demselben Verfahren erhalten wir also einmal eine irrationale und einmal eine rationale Zahl. Der einzige Unterschied ist die Form der Kurve. Man kann also aus einer Unterteilung in unendlich viele Rechtecke, die die Kurve annähern (bzw. exakt nachbilden) nicht folgern, daß das Ergebnis irrational sein wird.

Z.

@Noumenon
Da Wurzel 2 irrational ist, hat die Zahl in jedem Stellenwertsystem unendlich viele nichtperiodische Nachkommastellen und lässt sich deshalb auch im Dezimalsystem nur näherungsweise darstellen. Die ersten 50 dezimalen Nachkommastellen lauten:
sqrt2 = 1,41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 …
Keine Ahnung warum Dein Taschenrechner nur 9 Stellen aufzeigt ?

@zaeld
Ok, bei der Berechnung des Flächeninhaltes einer Parabel an sich, muss ich Dir Recht geben.
Ich habe etwas anderes gemeint und mich zu flach ausgedrückt.
Was ich sagen wollte ist, daß bei jeder Berechnung bei der Pi verwendet wird, immer wieder nachgelegt werden kann, einfach deshalb weil immer wieder jemand kommen kann und rechnet nochmal mit mehr Stellen von Pi das ganze nach. Selbst wenn ich ein ganzzahliges Ergebnis vorgebe für den Flächeninhalt eines Kreises, muß entweder r oder U irrational werden, je nachdem welche Formel ich verwende.
@Noumenon
Somit ist auch klar, daß der Flächeninhalt unterhalb Deiner Sinuskurve genau 1 ist, jedoch wird eine Sinuskurve durch Pi-Intervalle unterteilt, wenn ich Dich also nach der Bogenlänge Deiner Sinuskurve befragen würde oder nach der Bogenlänge einer Parabel, so würde man die Sinus oder die Kosinusfunktion benutzen, diese Funktion im Taschenrechner wiederum beruht auf einen festgelegten endlichen Wert für Pi. (Rad)sin(Pi/2)=1 wird euer Taschenrechner ausgeben, ein besserer Taschenrechner würde jedoch mit dem Wert, der vorher für Pi verwendet wurde 0,9999.... ausspucken. Alle Bestandteile die eine runde, geschwungene oder bogenförmige Geometrie beschreiben sind gemeint, entweder ist es der Flächeninhalt, der Umfang, der Radius bzw. die Bogenlänge die nicht endlich genau beschrieben werden kann.

Falls ich mich irren sollte, bitte ich um ein Zahlenbeispiel, wo alle genannten Bestandteile jeweils endliche Ergebnisse liefern.

@zaeld

zaeld schrieb:Damit ist gemeint, daß du z.B. ein rechtwinkliges Dreieck genauso wie einen Kreis durch viele kleine Rechtecke annähern kannst.

Würde man da nicht automatisch zu Trapez-Formen zur Annäherung greifen statt Rechtecke und die Sache wäre endlich ?

@skmo

skmo schrieb:Was ich sagen wollte ist, daß bei jeder Berechnung bei der Pi verwendet wird, immer wieder nachgelegt werden kann, einfach deshalb weil immer wieder jemand kommen kann und rechnet nochmal mit mehr Stellen von Pi das ganze nach.

Das ist richtig. Das basiert allerdings auf dem Wissen, daß Pi irrational ist. Die ursprüngliche Aussage, die ich kritisierte, war jedoch, daß sich die Irrationalität von Pi durch irgendetwas ergeben würde. Das sind also zwei völlig unterschiedliche Dinge.

skmo schrieb:Selbst wenn ich ein ganzzahliges Ergebnis vorgebe für den Flächeninhalt eines Kreises, muß entweder r oder U irrational werden, je nachdem welche Formel ich verwende.

Das kann man noch viel direkter formulieren: Pi ist ja als U/d definiert (bzw. U/2r),
und Pi ist irrational. Wären U und d beide rational, wäre U/d rational und damit Pi rational, was ein Widerspruch ist. Also ist entweder U oder d (oder beide) irrational.

So muß man nicht über die Fläche gehen.

skmo schrieb:Würde man da nicht automatisch zu Trapez-Formen zur Annäherung greifen statt Rechtecke und die Sache wäre endlich ?

Integralrechnung geht aber immer über Rechtecke, ist ja auch am einfachsten zu rechnen, einfach Breite mal Höhe. Zumindest die Herleitung der Integralrechnung; bei der Anwendung der Integralrechnung am Ende macht man ja gar keine Iterationen mehr, sondern nutzt die Erkenntnisse aus den Überlegungen zur Integralrechnung.

Mein Beispiel sollte ein universelles Verfahren anwendbar für unterschiedliche Kurvenformen sein. Wenn man anfängt, bestimmte Kurvenformen doch wieder anders zu behandeln, wäre es kein universelles Verfahren mehr. Deshalb bekommt jede Kurve Rechtecke hineingepflanzt.

Und welche Sache sollte endlich sein?

Z.

@zaeld
Na Du hast doch geschrieben:

zaeld schrieb:bei einem rechtwinkligen Dreieck die beiden kurzen Seiten wie bisher, und die lange Seite wird dann eine Treppe mit vielen Ecken. Bei unendlich kleinen Rechtecken hat man dann undlich viele Treppenstufen auf der langen Seite und damit auch wieder ein Unendlicheck

Und meines Wissens gibt es durchaus Integralrechnung nicht nur mit Rechtecken:

Die Trapezregel beschreibt ein mathematisches Verfahren, wie man das Integral einer Funktion im Intervall [a, b] numerisch annähert. Das entspricht der Fläche unter der Kurve f(x) bei kartesischer Darstellung.
Dazu ersetzt man die Fläche unter der Kurve durch ein Trapez, oder bei Stückelung des Intervalls durch mehrere Trapeze.

...würde bei einem Dreieck nicht zu einem Unendlicheck führen.
Hast Du nun eigentlich bezüglich meiner letzten Frage ein Zahlenbeispiel ?

skmo schrieb:Und meines Wissens gibt es durchaus Integralrechnung nicht nur mit Rechtecken:

Sicherlich kann man für Näherungsberechnungen auch andere Verfahren anwenden. In meinem Beispiel sind es aber wie beim Kreis nun einmal Rechtecke, woraus sich auch bei dem Dreieck ein Unendlicheck ergibt. Und nun?

Die eigentliche Integralrechnung benutzt auch Rechtecke. So ein Integral hat ja im allgemeinen die Form "S f(x) dx", wobei S für dieses Integralzeichen stehen soll. Das bedeutet, daß die Fläche eines Rechtecks berechnet wird: Das Rechteck mit dem linken Rand an Position x hat an dieser Stelle die Höhe f(x) und die infinitesimal kleine Breite dx. Mit "f(x) * dx" erhält man also die Fläche dieses infinitesimal schmalen Rechtecks an Position x. Das macht man mit allen Positionen entlang des Bereichs, über das man berechnen möchte und addiert die Flächen sämtlicher Rechtecke. Diese Summierung über alle Rechtecke wird durch das Integral-S gekennzeichnet.

skmo schrieb:Hast Du nun eigentlich bezüglich meiner letzten Frage ein Zahlenbeispiel ?

Nein, ich habe jetzt auch nicht nach einem gesucht. Daß da irgendeine Komponente bei Umfang, Radius, Fläche etc. immer irrational sein muß, ist eine Erkenntnis, die am Ende steht, wenn man die Eigenschaften der Komponenten kennt. D.h. wenn man bereits weiß, daß Pi irrational ist, kann man die Irrationalität des Umfangs oder des Radius herleiten. Allerdings kann man nicht umgekehrt auf die Irrationalität von Pi schließen, wenn man einen Kreis mit einem rationalen Radius in unendlich viele Rechtecke unterteilt.

Z.

@zaeld
Du hattest mich ja noch gefragt:

Die Irrationalität gibt es auch bei eckigen Berechnungen. siehe Wurzel aus 2

Ja, und?

Es ist ja hierbei so, daß die "Schuldigkeit" der Irrationalität von Pi, hierbei durch Summe der Wurzelfunktionen verursacht wird bei der Integralrechnung. :)
Wurzel aus 24/25 etc...
Deshalb habe ich vor 2 Seiten auch darauf hingewiesen.
Siehe nochmals http://www.mathematrix.de/flacheninhalt-kreis-herleitung-pi/

Noumenon schrieb:Pi wird nicht hergeleitet, sondern definiert... und zwar als Verhältnis von Umfang eines Kreises zu seinem Durchmesser.

Herleitung und Definition sind zwei paar Schuhe mein lieber @Noumenon

Noumenon schrieb:Auch "Annäherung" scheidet also als jedwedes Argument für Irrationalität aus...

Nö, denn Annäherung ist nicht gleich Annäherung, daraus alleine ergibt sich einfach noch kein Beweis für die Irrationalität.

@zaeld

zaeld schrieb:Da man selber unterteilt, weiß man das ja. Allerdings kommt wegen der unendlichen Unterteilung nicht unbedingt eine irrationale Zahl heraus.

Da hast du natürlich recht, denke ich verstehe nun worauf du hinaus willst. Die "irrationalität" einer Zahl festzustellen bzw. zu Beweisen ist ein wenig komplexer. Eine irrationale Zahl ist unendlich, jedoch ist nicht jede unendliche Zahl irrational.

zaeld schrieb:Wie lautet die Schlußfolgerung denn nun? "Weil man für die Berechnung von Pi ein Unendlicheck konstruiert, muß Pi irrational sein"?

Nein, ich kann höchstens sagen "sie könnte irrational sein, für den Beweis braucht es aber mehr als nur die Feststellung der Unendlichkeit von pi, wie ich oben bereits erwähnte.

zaeld schrieb:Um sich klar zu machen, daß eine Unterteilung in unendlich viele Rechtecke nicht zwingend zu einem irrationalen Ergebnis führt:

Eigentlich Logisch, die ursprüngliche Aussage bezog sich ja auch auf die Unendlichkeit von Pi und nicht auf die Irrationalität davon.

@skmo

skmo schrieb:Es ist ja hierbei so, daß die "Schuldigkeit" der Irrationalität von Pi, hierbei durch Summe der Wurzelfunktionen verursacht wird bei der Integralrechnung.

Na das ist doch mal eine Aussage, die bisher noch nicht gefallen ist, und an der etwas dran sein könnte. Die fehlte allerdings in der Behauptung, die die ganze Diskussion auslöste.

Jetzt muß man nur noch feststellen, ob das tatsächlich der Fall ist. Denn es gibt ja schließlich auch Wurzelziehungen, bei denen das Ergebnis rational ist.

@Bumbelbee

Bumbelbee schrieb:Eigentlich Logisch, die ursprüngliche Aussage bezog sich ja auch auf die Unendlichkeit von Pi und nicht auf die Irrationalität davon.

Ich gehe die ganze Zeit davon aus, daß mit "Unendlichkeit von Pi" genau die Irrationalität davon gemeint ist. Was ist denn ansonsten damit gemeint?

Mir schwant da etwas: Ist mit Unendlichkeit von Pi gemeint, daß die Verfahren zur Berechnung von Pi unendlich viele Teilkomponenten verwenden, also konkret die Summe über unendlich viele Einzelterme?

Bumbelbee schrieb:Nein, ich kann höchstens sagen "sie könnte irrational sein, für den Beweis braucht es aber mehr als nur die Feststellung der Unendlichkeit von pi, wie ich oben bereits erwähnte.

Abgesehen davon, daß mir wie gesagt noch nicht klar ist, was in dem Zusammenhang mit Unendlichkeit gemeint ist, ist das doch schon mal ein Konsens.

Z.

@zaeld

zaeld schrieb:Ich gehe die ganze Zeit davon aus, daß mit "Unendlichkeit von Pi" genau die Irrationalität davon gemeint ist.

Ich verstehe nicht wo du in der untenstehenden Aussage die Behauptung der Irrationalität siehst? Vieleicht check ichs ja grad einfach selber nicht ;)

skmo schrieb:Beste Antwort, weil wir tatsächlich nur "eckig" Flächeninhalte errechnen können, selbst die Integralrechnung ist eine Annäherung mit eckigen Körpern um die Flächeninhalte der wildesten Formen nachzustellen.

--------

zaeld schrieb:Mir schwant da etwas: Ist mit Unendlichkeit von Pi gemeint, daß die Verfahren zur Berechnung von Pi unendlich viele Teilkomponenten verwenden, also konkret die Summe über unendlich viele Einzelterme?

Mal ganz einfach gefragt, weshalb hat Pi unendlich viele Nachkommastellen?

@Bumbelbee

Bumbelbee schrieb:Ich verstehe nicht wo du in der untenstehenden Aussage die Behauptung der Irrationalität siehst?

Das "Beste Antwort" bezieht sich auf diese Aussage:

"weil Pi, meines Wissens, zur Annäherung an ein Unendlicheck genutzt wird (Kreis) und da dieser bekanntlich über unendlich viele Ecken verfügt muss die Zahl auch unendlich lang sein."

Unendliche lange Zahl heißt für mich irrationale Zahl. Unendlich lang bezieht sich ja wohl auf die Nachkommastellen...

Bumbelbee schrieb:Mal ganz einfach gefragt, weshalb hat Pi unendlich viele Nachkommastellen?

Es ist eben einfach eine Eigenschaft der Zahl Pi, irrational zu sein und damit unendlich viele Nachkommastelle zu haben. Es gibt keinen Grund dafür.

Es ist aber andererseits auch nicht weiter verwunderlich, weil es viel mehr irrationale als rationale Zahlen gibt.

Und was meinst du nun mit "Unendlichkeit der Zahl Pi", wenn damit nicht die Irrationalität gemeint ist?

Z.