Kann Pi plötzlich enden?

Man kann aber im Übrigen durchaus einen zu IR Isomorphen Körper finden in dem pi nicht unendlich viele nachkommestellen hat.

Just saying!

@zaeld

zaeld schrieb:Vielleicht ist das so, vielleicht auch nicht. Aber das genügt schon als Gegenbeispiel um aufzuzeigen, daß man alleine aus einer Approximation durch sehr viele bis unendlich viele Rechtecke eben nicht auf Irrationalität schließen kann.

Irgendwie doch, würde ich sagen. Es ist einfach der falsche geometrische Grundkörper für die Integralfunktion. Hätte man andere bogenförmige Geometrien die restlos einen Kreis ausfüllen könnten und selbst ohne Pi oder einen anderen irrationalen Wert auskämen, würde es gehen.
Eine Parabelfunktion die exakt einen Halbkreis beschreibt bräuchte kein Pi, jedoch würde ihr Parabelbogenlänge wiederum sich nur mit Hilfe von Pi beschreiben lassen. Ohne sin,cos etc, dem Pi zugrunde liegt geht´s nicht.
Letztendlich ist Dein Beispiel mit dem Dreieck und den Stufen deshalb endlich, weil ein Dreieck sich genau 2mal in Deine Integralgeometrie einfügen lässt, ohne Rest.

Selbst wenn man Dein Dreieck mit unendlich vielen Punkten füllt, stellt sich die Frage:
Was ist ein Punkt ?
Für Dein Dreieck würde man ihn als unendliche kleines Quadrat definieren MÜSSEN, weil sonst
Das Einheitsdreieck: 1/2g x h =1x0,5= 0,5 ebenfalls zu einer unendlichen Zahl führen würde, wenn man sagen würde "der unendlich kleine Punkt ist rund":



Hierbei ist es umgekehrt, die runde geometrische Integralgeometrie ist ungeeignet etwas eckiges zu beschreiben, das Ergebnis 1/2gxh würde ebenfalls eine irrationale Zahl für Dein Dreieck ausspucken.

wenn man sich mit der mathematik einlässt, dann verändert sich nicht die mathematik. Die Mathematik verändert dich.

Ich find den hype um pi ziemlich sinnlos. Ihr auch?

Es gibt unendlich viele andere irrationale zahlen, aber an pi geilen sich alle auf. Meist erkennt man daran Leute die mehr so ein rudimentäres interesse an populärwissenschaft haben.

Warum nicht e?

@skmo

skmo schrieb:Irgendwie doch, würde ich sagen. Es ist einfach der falsche geometrische Grundkörper für die Integralfunktion. Hätte man andere bogenförmige Geometrien die restlos einen Kreis ausfüllen könnten und selbst ohne Pi oder einen anderen irrationalen Wert auskämen, würde es gehen.

Und dieser Unterschied soll ausmachen, ob das Ergebnis der Approximation rational oder irrational sein wird? Das finde ich überhaupt nicht anschaulich. Gibt es dafür noch irgendeine Begründung?

Z.

zaeld schrieb:Ob es sich bei Pi um eine irrationale Zahl handelt, lese ich aus dem Titel.

Ja genau! :D ...

zaeld schrieb:Da, schon wieder. Was soll denn eine "Unendlichkeit einer Zahl" sein?

Ich fragte ja schon, ob damit die Anzahl der Nachkommastellen gemeint ist, aber zu einem eventuellen "Ja" oder "Nein, sondern damit ist gemeint, daß..." kannst du dich ja leider nicht durchringen.

Aha, Ich merke schon, du versuchst mir einen Strick daraus drehen das ich Pi als unendlich bezeichne weil sich die Nachkommastellen unendlich weiter berechnen lassen.

Was du hier machst ist Wortklauberei. Keine Ahnung ob dus letztendlich verstanden hast oder nicht.... naja für mich hat sich die Diskussion hier erledigt, Sinnlos da kann ich @shionoro nur zustimmen ;)

Also aus einer approximation kann man nicht darauf schließen, dass etwas irrational ist.
Insofern muss ich zaeld recht geben.

Dass pi irrational ist kann man beweisen, und das ist auch gar nicht schwer.

Man kann natürlich sehr wohl aus der definition von pi auf irrationalität schließen also letztendlich aus der reihendarstellung.

Aber je nachdem was man als approximation versteht kann man daraus natürlich auf gar nix schließen.

@Bumbelbee

Bumbelbee schrieb:Aha, Ich merke schon, du versuchst mir einen Strick daraus drehen das ich Pi als unendlich bezeichne weil sich die Nachkommastellen unendlich weiter berechnen lassen.

Was ist los? Ich frage dich, was "Unendlichkeit einer Zahl" sein soll, du antwortest erst nicht, und jetzt unterstellst mir, ich würde irgendeinen Strick daraus drehen wollen?

Bumbelbee schrieb:Was du hier machst ist Wortklauberei.

Nein, du sagst, Irrationalität und "Unendlichkeit einer Zahl" wären etwas unterschiedliches, willst aber nicht verraten, was "Unendlichkeit einer Zahl" denn überhaupt sein soll.

Damit hat sich die Diskussion dann tatsächlich erledigt.

@shionoro

shionoro schrieb:Dass pi irrational ist kann man beweisen, und das ist auch gar nicht schwer.

Unbestritten, aber eben nicht einfach damit, indem man sagt, daß für die Berechnung eines Näherungswertes ein Kreis in unendlich viele Rechtecke unterteilt wird und deswegen das Ergebnis unendlich lang sein muß.

shionoro schrieb:Man kann natürlich sehr wohl aus der definition von pi auf irrationalität schließen also letztendlich aus der reihendarstellung.

Kann man das? Die Reihendarstellung von 1/2 + 1/4 + 1/8 usw. hat ja auch immer nur rationale Näherungsergebnisse, trotzdem ist das Endergebnis eine natürliche Zahl. Vielleicht ist das Pi ja auch so.

Außerdem hat der ursprüngliche Satz, den ich kritisierte, gar nicht mit der Reihendarstellung argumentiert.

Zäld

http://www.fab.hs-rm.de/~dueck/mathematik/semester3/Lesen_wissenschaftlicher_Texte/Irrationalitaet.pdf

Um mal die Suche nach dem Beweis zu erleichtern.

@intruder
In Deinem pdf steht folgender komischer Satz:

Wenn π rational wäre, dann wäre auch π² rational. Es genügt also zu beweisen, dass π² irrational ist.
Wir nehmen das Gegenteil an, dass π² = a/b ist, für bestimmte positive ganze Zahlen a und b.

Die Wurzel aus 2 ist ebenfalls wie Pi eine irrationale Zahl, (Wurzel 2)² ist jedoch genau 2 und rational und für (Wurzel 2)² = a/b, gibt es auch 2 positive ganze Zahlen: 2/1=2, was nun ?

Wenn π rational wäre, dann wäre auch π² rational

Dieser Satz kann doch nicht stimmen. Oder ?

@zaeld
@zaeld

Ja kann man, weil du ja mit der reihendarstellung die Zahl genau definierst. wenn du über die definition der Zahl nicht die irrationalität folgern kannst, worüber dann? :p


Bei reihen macht man sowas über konvergenzüberlegungen.

Wurzel zwei ist auch unendlich summe rationaler zahlen, und du kannst dann eben beweisen, dass diese reihe Zwar konvergiert (so wie auch meine reihe oben konvergiert), aber du kannst eben auch beweisen, dass sie gegen keine rationale zahl konvergieren kann, also du keinen rationalen grenzwert angeben kannst, daher muss die Zahl irrational sein

@zaeld

zaeld schrieb:Und dieser Unterschied soll ausmachen, ob das Ergebnis der Approximation rational oder irrational sein wird? Das finde ich überhaupt nicht anschaulich. Gibt es dafür noch irgendeine Begründung?

Du hast Recht, stimmt tatsächlich nicht.
In dem folgendem Bild wurde es mir klar, wenn man das dort gegebene Quadrat mit Rechtecken approximiert, müsste nach meiner Erklärung ein rationales Ergebnis raus kommen, ist aber nicht so:

@skmo

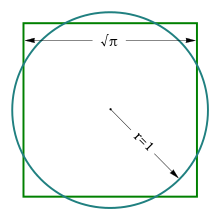
Wenn π rational wäre, dann wäre auch π² rational

Dieser Satz kann doch nicht stimmen. Oder ?

Es wird hier gesagt, daß das Quadrat einer rationalen Zahl rational sein muß. Nicht, daß die Wurzel einer rationalen Zahl es im Umkehrschluß ebenfalls sein müsse.

Das ist wie die Druckgeschichte von Corespin.

Nur weil man mit einem Hammer ein Glas zertrümmert bedeutet die nicht, dass man mittels eines Unterdruckes Gläser reparieren kann.

Nun gut :)
Bis zum 17. Jahrhundert hätte ich mit dem folgenden Bruch alle reinlegen können ;)

So stimmt x/y=226517876251716162692149071050771828410490449602080890536575346 / 72102879408277751642507260419334203501590758230297414247167791 mit Pi auf 86 Stellen überein!

Aber nur, weil du Pi schon kennst.

zaeld schrieb:Nein, du sagst, Irrationalität und "Unendlichkeit einer Zahl" wären etwas unterschiedliches, willst aber nicht verraten, was "Unendlichkeit einer Zahl" denn überhaupt sein soll.

Ich hab es dir mehrmals verraten, du wolltest es nicht verstehen und beschuldigst mich es nicht gesagt zu haben. Möchtest dus noch immer nicht verstehen oder Trollst du schon?

zaeld schrieb:Damit hat sich die Diskussion dann tatsächlich erledigt.

Immerhin ein Konsens.

@zaeld

zaeld schrieb:Kann man das? Die Reihendarstellung von 1/2 + 1/4 + 1/8 usw. hat ja auch immer nur rationale Näherungsergebnisse, trotzdem ist das Endergebnis eine natürliche Zahl. Vielleicht ist das Pi ja auch so.

Es ist jetzt eher als Anmerkung zum Thema Reihen zu verstehen, aber es gibt u.a. die namenhafte Wikipedia: Leibniz-Reihe - eine unendliche Reihe mit Grenzwert pi/4.
Ein möglicher Beweis dazu arbeitet mit dem Arkustangens, bspw. hier (http://en.wikipedia.org/w/index.php?title=Leibniz_formula_for_%CF%80&oldid=464980455#Proof nachzulesen) und der arctan selbst lässt sich auch wiederum als eine Reihe darstellen, siehe Wikipedia: Arkustangens und Arkuskotangens#Reihenentwicklung .

(Unendliche) Reihen begegnen einem immer wieder (vor allem die von e) und deshalb muss man auch (wie @shionoro ja schon sagte) Konvergenzbetrachtungen durchführen, um verstehen zu können, wohin einen eine Reihe überhaupt führt.
So kann man bspw. Sinus und Kosinus direkt über Reihen einführen.
Beim Stichwort Leibniz gelangt man zum Leibniz-Kriterium, was eine Aussage zur Konvergenz alternierender Reihen macht und daneben gibt es noch eine Vielzahl weiterer Kriterien.

Reihen und deren mögliche Konvergenz sind sehr ergiebige Themen und man sieht ja hier, dass man früher oder später nicht daran vorbeikommt, sich damit auseinanderzusetzen.

@shionoro

shionoro schrieb:Ja kann man, weil du ja mit der reihendarstellung die Zahl genau definierst. wenn du über die definition der Zahl nicht die irrationalität folgern kannst, worüber dann?

Pi wird aber nicht über die Reihendarstellung definiert, sondern als "Verhältnis von Umfang zu Durchmesser eines Kreises".

Aus dieser Definition (und weiteren Überlegungen) kann man dann diese Reihendarstellung ableiten, mit der man dann auch einen Wert berechnen kann. Aber nur, weil man da eine Reihendarstellung hat, heißt das ja noch lange nicht, daß das Ergebnis irrational ist.

shionoro schrieb:Bei reihen macht man sowas über konvergenzüberlegungen.

Habe ich nichts dagegen, daß man aus solchen Überlegungen auf die Irrationalität von Pi schließen kann. Allerdings war von solchen Überlegungen in

Beitrag von unecht (Seite 1)

nichts zu lesen. Da stand nur [Pi hat unendlich viele Nachkommastellen] "weil Pi, meines Wissens, zur Annäherung an ein Unendlicheck genutzt wird (Kreis) und da dieser bekanntlich über unendlich viele Ecken verfügt muss die Zahl auch unendlich lang sein."

Keine Reihe, Keine Konvergenzbetrachtung...

@Bumbelbee

Bumbelbee schrieb:Ich hab es dir mehrmals verraten, du wolltest es nicht verstehen

Was, wo hast du denn irgendwann mal erklärt "Mit Unendlichkeit von Pi meine ich, daß..."?

Stattdessen gab es Gegenfragen und Ratespiele:

Ich: Ich gehe die ganze Zeit davon aus, daß mit "Unendlichkeit von Pi" genau die Irrationalität davon gemeint ist. Was ist denn ansonsten damit gemeint?

Du: ("Was ist denn ansonsten damit gemeint?" wurde in der Beantwortung von dir weggeschnitten) Ich verstehe nicht wo du in der untenstehenden Aussage die Behauptung der Irrationalität siehst?

Ich: Mir schwant da etwas: Ist mit Unendlichkeit von Pi gemeint, daß die Verfahren zur Berechnung von Pi unendlich viele Teilkomponenten verwenden, also konkret die Summe über unendlich viele Einzelterme?

Du: Mal ganz einfach gefragt, weshalb hat Pi unendlich viele Nachkommastellen?

Ich: Und was meinst du nun mit "Unendlichkeit der Zahl Pi", wenn damit nicht die Irrationalität gemeint ist?

Du: Wenn wir mal die Nummerphilie beiseite legen und uns Bildlich vorstellen wie pi zustande kommt dann ist es meiner Meinung nach einfach einleuchtend das sie unendlich sein Muss (unendlicheck) (Keine Erklärung, was du unter "unendliche Zahl" verstehst)

Ich: Ja was heißt denn bei dir nun "eine Zahl ist unendlich"? Ist das eine Zahl, die unendlich viele Nachkommastellen hat, die nicht periodisch sind?

Du: Lies mal den Disskussionstitel und überlege dir was damit gemeint sein könnte.


Gut, anscheinend ist es dir nicht möglich, auf eine Frage eine klare Antwort zu geben, selbst wenn es nur ein "Ja" oder "Nein" wäre. Dann nehme ich das mal so hin.

Vielleicht habe ich den Post ja auch überlesen, wo es eine klare Antwort gab. Glaube ich aber nicht.

@zaeld

Naja, diese geometrischen kisten definierst du alle über sinus und cosinus und die definiert man über die verhältnisse von katheten auf dreiecken, und für sinus und cosinus gibt es reihen aus denen man dann letztendlich pi folgern kann.

Die begründung 'weil man mit pi ein unendlicheck annährt' ist natürlich nicht richtig^^

Pi ist schließlich nicht in jedem denkbaren zahlensystem irrational.
Ich könnte genausogut alle zahlen die es gibt durch pi teilen.
Dann wäre pi im neuen zahlensystem die 1 und 1 wäre 1/pi und damit irrational.
Gewinnen tu ich damit nix, natürlich, aber das heißt, dass der kreisumfang nicht zwangsläufig irraitonal ist.

Das wäre dann aber der kreisradius bei nem rationalen Kreisumfang :p