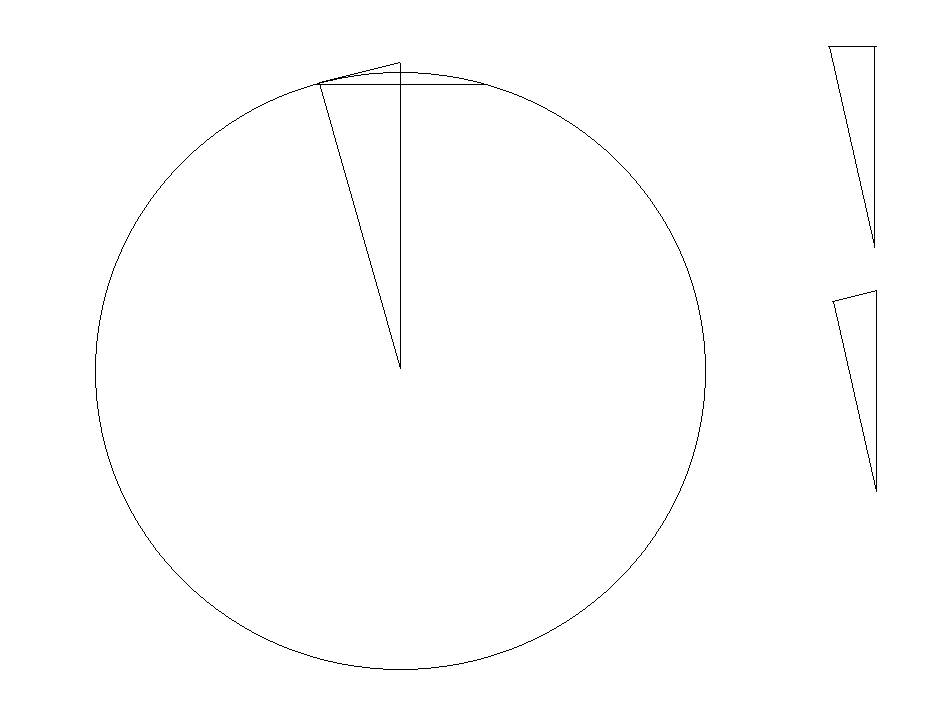carsten_167 schrieb:wir brauchen ja die tangentiale Abweichung .. nicht den Wert der Krümmungshöhe ... diese tangentiale Abweichung habe ich geometrisch mit einem Lineal und der Tatsache dass der Kreis nicht im rechten Winkel also tangential anschließt wo er sollte , geschätzt und dann dividiert, weil es ja geometrisch linear ist...hab ich zumindest so gedacht
Was auch immer Du willst, ich rate mal hierzu:
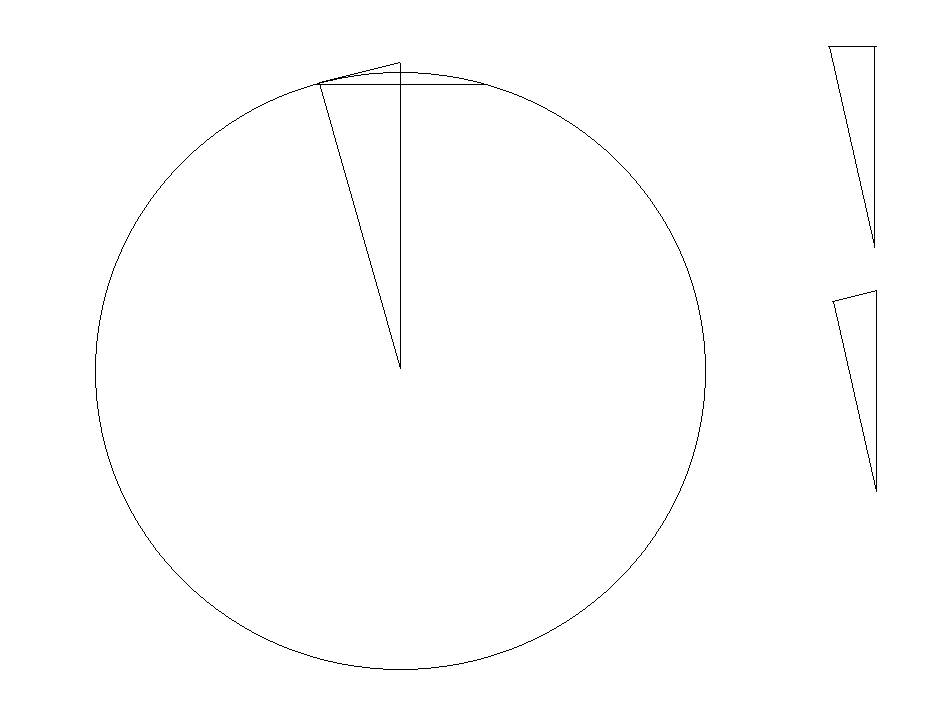
und dazu noch diese Seite zum Rechnen:
Rechts von meiner Zeichnung der Erde siehst Du zwei rechtwinklige Dreiecke, die Du auch im Hauptbild eingezeichnet findest. Der untere, der spitze Winkel in beiden Dreiecken liegt am Erdmittelpunkt. Mit der Größe dieses Winkels und dem Erdradius (im oberen wie unteren Dreieck die linke Seite) kannst Du auf der verlinkten Seite die Länge der rechten Seite berechnen. Imoberen Dreieck ist diese rechte Seite etws kürzer als der Erdradius, im unteren etwas länger. Das liegt daran, daß die obere Seite des oberen Dreiecks die Sekante ist, die innerhalb der Erdkrümmung gerade verläuft, und im unteren Dreieck ist es die Tangente.
Wenn Du nun (wie es auch in der vonDir verlinkten Seite berechnet wird) wissen willst, wie hoch sich die Erdkrümmung als Hügel zwischen Start und Zielpunkt erhebt, mußt Du in meiner verlinkten Seite bei "alpha" die hälfte des oben angegebenen Winkels eintragen (also 0,002083[3periode]) und den äquatorialen Erdradius (laut
Wikipedia: Erdradius am Äquator 6.378.137 Meter) ins Fenster der Seite "c". Wenn Du hingegen wissen willst, wie weit oberhalb des Erdbodens eines Erdpunktes eine Gerade entlangläuft, die "in einer Rotationssekunde Entfernung"am Boden im rechten Winkel zur Lotrechten losgeht, dann mußt Du den vollenWinkel bei "alpha" eintragen (also die 0.004166666...) und den Erdradius bei "b".
Du wirst feststellen, daß der Höhenunterschied in der ersten Rechnung nicht mal einen, in der zweiten nicht mal zwei Zentimeter beträgt.
Da dieser Rechner automatisch auch den Wert der Seite a ergänzt, kannst Du erstens sehen, daß dieser Wert der nichtgeraden Oberflächenentfernung der beiden Äuqatorpunkte entspricht, die der Strecke für "eine Sekunde Erdrotationsbewegung" entspricht (in der ersten Rechnung natürlich nur die Hälfte davon), was zeigt, wie minimal die Krümmung hier noch ist. Und zweitens kannst Du nun mit dem Satz des Pythagoras a²+b²=c² gegenprüfen, ob die Längenverhältnisse und damit die behauptete Abweichung vom Erdradius korrekt sind/ist oder nicht.
Den Rest Deines Beitrags samt Nachtrag klemm ich mir lieber.
