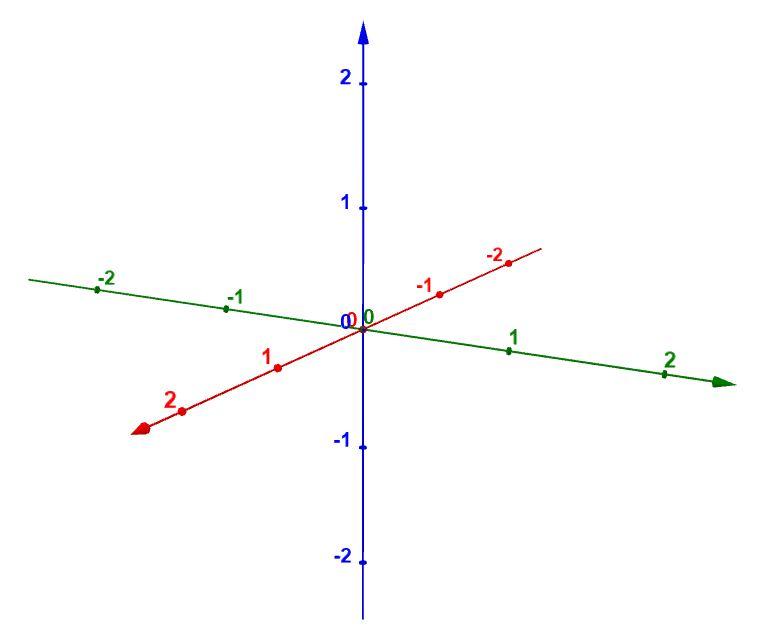
@Kephalopyr Es gibt 3 Linien, die können gerne auch X,Y,Z sein, dazu nehmen wir den Punkt M.
Zum Gegenbeweis nehmen wir Linie Q dazu.
Zwei Linien die sich kreuzen liegen immer in einer Ebene
X (grün) kreuzt Y bei M im Winkel von 90°, diese zwei liegen auf der XY Ebene.
X (rot) kreuzt Z bei M im Winkel von 90°, diese zwei liegen auf der XZ Ebene.
Y (blau) kreuzt Z bei M im Winkel von 90°, diese zwei liegen auf der YZ Ebene.
Jeder der Linien hat zwei "Partner" und zu jeder Zeit 90° zu beiden.
Gegenbeweis: Q kann diese Bedingungen nicht erfüllen, entweder sind die Winkel nicht mehr 90° und wenn, liegt sie auf auf X,Y oder Z (kollinear)
 https://de.serlo.org/mathe/2043/zeichnen-im-3d-koordinatensystem
https://de.serlo.org/mathe/2043/zeichnen-im-3d-koordinatensystem
Abahatschi schrieb am 23.06.2022:Tun wir das? Welche sehen wir außer den 4 bekannten und mit welcher Technologie?
Abahatschi schrieb am 23.06.2022:Richtig und genau deswegen können mehrdimensionale Objekte >4D in unserem Raum existieren.



