Das Geburtstagsparadoxon

@perttivalkonen
Ich gratuliere, bei mir war das nicht so. Wenn ich so zurück denke, kam sowas nur einmal vor,
in der Lehre, da hatte eine am gleichen Tag Geburtstag wie ich, da war das so ;) Ich war seit der Vorschule in ca. 9 verschiedenen Klassen/Gruppen (Schulwechsel, eine Eherenrunde usw.), und es kam nur einmal vor.

Zum Geburtstag von 3/4 meiner Familie kenne ich Menschen, die am selben Tag Geburtstag haben.

Natürlich deckt die statistische Streuung das auch ab, daß ein Einzelner auch mal nur mit Gruppen zu tun hat, in denen Doppelgeburtstage so gut wie nie auftreten. Wenn beim Würfel laut Statistik jede Augenzahl mit Wahrscheinlichkeit 1/6 vorkommt, kann es dennoch passieren, daß Du 10 mal hintereinander die selbe Zahl würfelst. Wahrscheinlicher, als daß Du unter hundert Würfen eine Punktzahl nicht würfelst.

Multiversum schrieb:Ich verwette meinen rechten Schuh darauf,
das es aber nicht so ist.

Weil Bauchgefuehl oder wie? :-)

@Rho-ny-theta

Die Gleichverteilung muesste doch eine untere Schranke darstellen. Je verzerrter die Verteilung ist, desto wahrscheinlicher wird eine Kollision doch, bis zum Extremfall mit 100%, oder irre ich mich da?

Fuer allgemeine Verteilungenen P(i) sieht man das ja schon bei 2 Leuten.
Die Wahrscheinlichkeit dass 2 Personen nicht am gleichen Tag Geburtstag haben ist:
sum_i p(i) * (1 - p(i)) = 1 - sum_i p(i)^2
Bin jetzt zu muede fuer den n Leute Fall, aber die Wahrscheinlichkeit muesste in der Realitaet deutlich hoeher sein durch die Geburtenverteilung.

@McNeal
Ne, Realität...

@Multiversum

Wenn du von deinen persoenlichen Erfahrungen Statistiken ableitest, dann ist das nicht mehr als ein Bauchgefuehl.

@McNeal
Tut mir leid, leider fehlen mir die Mittel, um es dir an Hand einer representativen Umfrage
darzulegen. Kannst ja mal bei Emnid anfragen^^ Aber mal andersherum, was, außer den fiktiven Zahlen, hast du um die These zu beweisen?

@Multiversum

Im Wikipediaartikel steht aber nun, dass es mit "Echtdaten" übereinstimmt .. Du oder Wikipedia mhm..

Zum Thema Schulklassen, bei mir hatten manchmal sogar 3 Leute am selben Tag Geburtstag..

Und ich hab 2 Exen die beide am selben Tag wie ich Geburtstag haben..

@Multiversum
In der Stochastik kann die eigene Intuition unheimlich schnell aufs Glatteis geführt werden.
Die Methodik, die einem das Geburtstagparadoxon auswirft, die sagt einem beispielsweise auch, dass man beim 100-maligen Werfen einer Münze mit etwa 80%iger Wahrscheinlichkeit irgendwo eine Kette von 8 aufeinanderfolgenden Zahl- oder Kopf-Würfen hat.

Stellt man diese Aufgabe irgendjemandem, bspw. Schülern, neigen viele dazu eine solche Liste einfach zu fälschen, die aber leicht zu erkennen sind, weil viele intuitiv annehmen die Ergebnisse müssten mit einer gewissen Regelmäßigkeit einmal wechseln.

Es geht zwar eingangs um ein bestimmtes Paradoxon, aber das Thema Intuition ist scheint hier auch ein Knackpunkt in der Diskussion zu sein.
Dazu vielleicht auch einmal kleiner Ausflug in die Wikipedia: Bedingte Wahrscheinlichkeit , da diese Geschichte auch gern mal die eigene Intuition über den Haufen wird.

Ein Beispiel zum Thema Münzen werfen.
Die Wahrscheinlichkeit, dass man eine Münze 5 mal wirft und man 5 mal das gleiche Symbol erhält - das deckt sich noch mit der Intuition - ist gerade (1/2)^5 = 1/32 = 0,03125 - also etwa 3 Prozent.

Jetzt betrachten wir dazu eine bedingte Wahrscheinlichkeit:
Betrachten wir 20 Münzwürfe. Wieder wollen wir die Wahrscheinlichkeit für 5 mal Kopf bei den ersten 5 Würfen betrachten, sagen aber jetzt, dass wir bspw. dazu wissen, dass bei den 20 Würfen insgesamt genau 15 mal Kopf geworfen wurde.
Ändert diese Zusatzinformation das Ergebnis?
Intuitiv würfe man wohl "Nein." sagen, aber das ist die falsche Antwort.
Die Wahrscheinlichkeit ändert sich zu 1001/5168 = (rund) 0,1937 - also fast 20 Prozent.

Wessen Intuition noch nicht völlig verwirrt ist, dem kann man noch dazu sagen, dass diese ~20 Prozent auch auftreten, wenn man eine manipulierte Münze verwendet, d.h. wenn das Eintreten von Kopf die Wahrscheinlichkeit p und die von Zahl die Wahrscheinlichkeit 1-p hat.

---

Intuition und Zufallsexperimente haben nur eine kleine Schnittmenge, wie man gesehen hat.
Und man darf auch nicht vergessen, dass die Stochastik häufig so allgemeine Aussagen macht, die einer großen Zahl an Einzelexperimenten braucht, damit sich die Theorie mit der Realität deckt. (Stichwort: Gesetz der großen Zahlen)

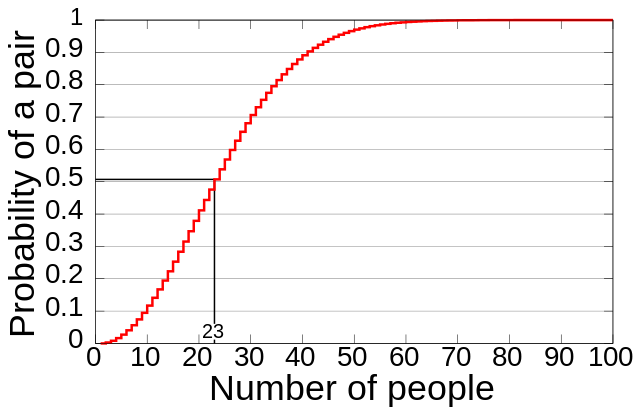
Ich persönlich habe in meinem Leben auch nur eine Person getroffen, die am selben Tag Geburtstag hatte wie ich. Dagegen hatte ich in meinem Umfeld (u.a auch in meiner Schulzeit) eine Hand voll von Personenpaaren, sogar eine Dreierkonstallation mit den selben Geburtstagen.
Letztlich sagt das Geburtstagsparadoxon auch nur wenig über den Einzelfall aus, sondern betrachtet halt "unendlich viele" solcher Einzelexperimente. Das sollte man nicht vergessen, wenn man sich in seinem Umfeld umschaut.

Multiversum schrieb:Aber mal andersherum, was, außer den fiktiven Zahlen, hast du um die These zu beweisen?

Mathematik, die auf Annahmen aufbaut. Du kannst entweder die Annahmen anzweifeln oder einen Fehler im Beweis finden. Im uebrigen sind das keine fiktiven Zahlen sondern Wahrscheinlichkeiten. Die Intuition versagt bei denen gerne mal; auch schoen bei anderen Raetseln zu sehen.

Die Annahmen: Das Jahr hat 365 Tage, die Geburtstage sind gleichverteilt und unabhaengig. Die Gleichverteilung sorgt dafuer, dass die Wahrscheinlichkeit fuer gleiche Geburtstage leicht veringert wird, es bringt also nix diese Annahme anzugreifen.
Bleibt noch die Unabhaengigkeit, die ich auch fuer gegeben halte weil das Kinderkriegen ja nicht mit den andern Eltern in einer Klasse abgesprochen wird und sowieso relativ schlecht zu planen ist weil man ja nie weiss, wanns klappt. Mir waere auch nicht bewusst dass beim Zusammenstellen der Schulklassen versucht wird eine Geburtstagkollision zu vermeiden.

Der 'Beweis':
Wahrscheinlichkeit selben Geburtstag von 2 Leuten bei insgesamt

n=2 Leuten 1 - (365-1) / 365 = 0.00273972602
n=3 Leuten 1 - (365-1) * (365-2) / 365^2 = 0.00820416588
n=4 Leuten 1 - (365-1) * (365-2) * (365-3) / 365^3 = 0.01635591246
...
n Leuten 1 - Produkt_i=1..n [ (365-i) / 365 ]
Der Plot sieht dann so aus:

Und ab 23 Leuten ist die Wahrscheinlichkeit > 50%.

Ich glaube du hast gerqten @Mayar ..du wusstest nivhtmal worums geht..sieht man an deiner frage anfangs :D auch dein loesungsvorschlag is wirr :) aber nichts fuer ungut..weitermachen.

mrfeelgood schrieb:Im Wikipediaartikel steht aber nun, dass es mit "Echtdaten" übereinstimmt .. Du oder Wikipedia mhm..

wir haben auf seite vorher auch den grund dafür gesehen, die geburten sind zwar nicht gleichmäßig übers jahr verteil, der wechsel der hauptgeburtssaison sorgt aber dafür das eine normalverteilung bei schlecht angelegten untersuchungen vorgegaukelt wird.

Paradox finde ich auch, dass dieser Thread an meinem Geburtstag eröffnet wurde.
Wie wahrscheinlich ist das, wenn man sich sogar den Titel anschaut? :)

52 - Wochen
23 - Gäste
Bis 52 sind es 15 Primzahlen. Da wir nun das ganze mit den Gästen vergleichen kommt der Faktor der Primzahlzwillinge hinzu.

um die 60 przt ergo

@Mayar
Also wenn du schon einen Thread eröffnest, dann schreibe doch bitte im Threadeingang mehr Informationen rein.

Wie lautet nun das Rätsel wirklich?
2 Menschen haben an einen Tag Geburtstag und 23 menschen kommen hinzu???

Sogar die Wahrscheinlichkeit auf einen Sechser im Lotto beträgt 50%...

...entweder gewinnste oder eben nicht.

Und wieso sagt Lotto selbst dann, dass die Wahrscheinlichkeit auf einen 6er im Lotto bei 1 zu 139.838.160 liegt?

--> https://www.lotto.de/de/informationen/lotto-6aus49/gewinnwahrscheinlichkeit.html (Archiv-Version vom 13.01.2016)

Du meinst wohl eher, die Chance (den Jackpot) zu gewinnen liegt bei 50/50 ;)

@Zerox

Alles ist 50/50
Ist doch einfacher so, als irgendwelche berechnungen anzustellen.
Entweder klappt etwas...oder nicht ;)