Naja, das gilt für die Eigenzustände in einem idealisiertem Coulombschen Potential, mit einem idealisierten Elektron das seine Energie aus eben diesem Potential bezieht. Überlagerungen von Eigenzuständen sind dann logischerweise nicht mehr statisch, weil durch die unterschiedlichen Eigenfrequenzen es zu anderen Beträgen kommt.
Aber das ist alles nicht so kompliziert wie es auf den ersten Blick scheint. Man muss es nur richtig erklären können:
Fangen wir mal mit einem simplen Potentialtopf an:
http://www.falstad.com/qm1d/ (Archiv-Version vom 06.02.2012)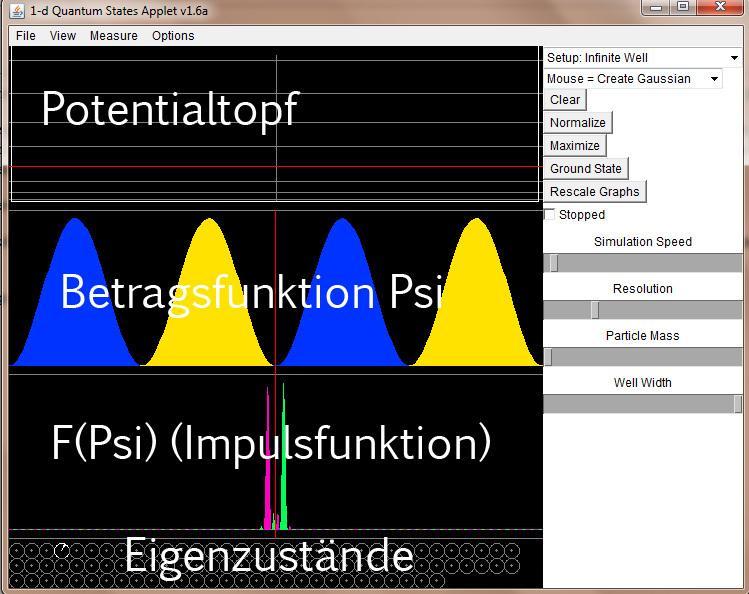
Original anzeigen (0,2 MB)Oben siehst du den Potentialtopf, alles ist auf dem Niveau Null, die Ränder auf unendlich hohem Potential. Dazwischen ist das Teilchen, das diesem Potential folgt. Eingezeichnet sind des weiteren die berechneten Eigenzustände, das sind die Querlinien. Die kannst du anklicken, wodurch du das System in diesen Zustand überführst.
Das mittlere Fenster ist dann die Wellenfunktion des Teilchens. Lass dich erstmal von dem farbigen Geblinke nicht verwirren. Du kannst es ausstellen, in dem du View->Wave Function->Probability wählst.
Die obere Grafik ist der Betrag, die untere ist die Fouriertransformierte, also der Impuls des Systems.
Wählst du also oben die verschiedenen Energiezustände aus siehst du die zu erwartenden Sinus² Beträge, die sich ja ganz einfach aus der zeitunabhängigen Schrödingergleichung ergeben.
So, jetzt wirds interessant. Such dir einen Energiezustand aus, und dann wähle View->Wave Function-> Real + Imaginary Parts.
Du siehst, dass der Eigenzustand sich aus zwei Komponenten zusammensetzt (blaue und weiße Linie). Das eine ist der reale, der andere der imaginäre Anteil der Wellenfunktion. Diese beiden Funktionen treiben sich gegenseitig vorran und verhalten sich demnach entsprechend einer Welle (zwei Komponenten, die sich dynamisch vorrantreiben).
Die Zeitabhängige Schrödingergleichung spuckt dir diese beiden Funktionen aus.
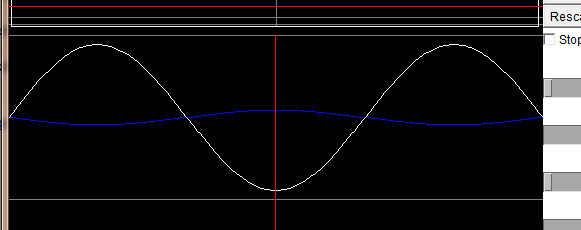
Was dir auffallen wird: Im Eigenzustand sehen der reale und der imaginäre Anteil genau gleich aus. Sie sind einfach um 90° phasenverdreht. Das gilt für alle Eigenzustände.
Was auch auffällt: Je mehr Energie das System hat, desto schneller dreht sich die Phase.
Richte jetzt deinen Blick ganz nach unten ans Fenster. Dort siehst du Kreise, wobei alles still stehen, und einer sich dreht. Dies ist der aktuelle Zustand, und seine Phase. Wählst du verschiedene Zustände aus so werden sich verschiedene Phasen drehen.
Du kannst die Kreise auch direkt anklicken und somit mehrere Zustände gleichzeitig anwählen. Das System befindest sich dann in dem berühmten "Schwebezustand", wo die Katze sowohl lebendig, als auch tot ist ;-)
Mit Magie hat das allerdings nicht viel zu tun, es werden einfach die Real- und Imaginäranteile addiert.
Lass dir jetzt wieder den Betrag anzeigen. Nun wird das System nicht mehr still stehen, sondern umherwabern.
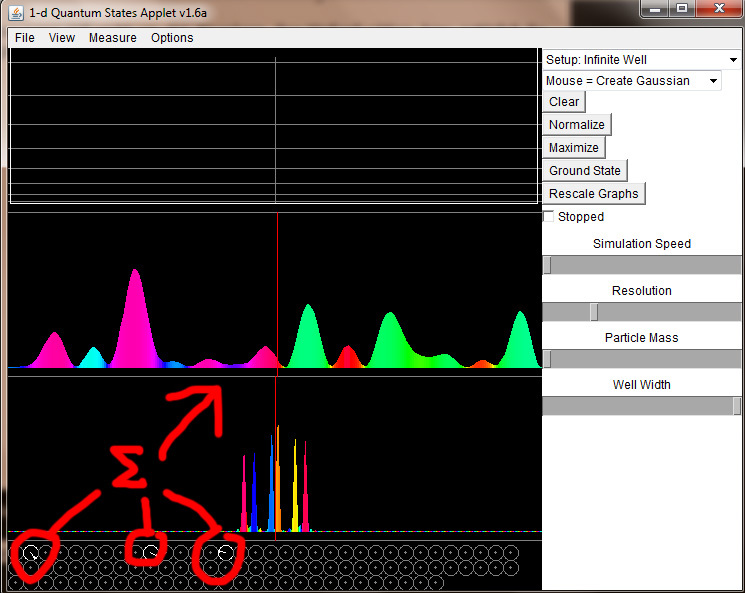
Du kannst in Betragsfunktion hineinklicken und direkt eine Gaußglocke injizieren, mit der du das System initialisieren möchtest. Danach siehst du, wie die Wellenfunktion auseinander gleitet.
So, jetzt sehen wir uns mal einen "Quantensprung" an:
http://www.falstad.com/qm1drad/ (Archiv-Version vom 06.02.2012)Hier siehst du sofort einen Sprung vom ersten ins zweite Energieniveau. Dazu wird das Potential in einer bestimmten Frequenz gekippt, was man auch erkennen kann, wenn man genau hinschaut. Das Programm gibt dir auch die Möglichkeiten direkt in andere Zustände zu springen (die richtige Frequenz für den Sprung wird automatisch eingetragen) oder du kannst auch selber mit den Werten rumspielen.
Was du hieraus mitnehmen solltest ist ein Verständnis für den Quantensprung an sich, und was dabei mit der Wellenfunktion passiert. Ich denke hier kann man prima erkennen, was wirklich passiert und warum der Zustand während des Übergangs "undefiniert" ist. Ist natürlich alles stark vereinfacht, aber das Prinzip sollte klar werden.
Und wenn du das verstanden hast, dann kannst du dir das jetzt in einem dreidimensionalen Coulombpotential anschauen.
http://www.falstad.com/qmatomrad/Auch wird gleich eine Zustandstransition simuliert. Das ganze ist zwar nicht mehr so übersichtlich (weil dreidimensional) aber man sieht jetzt schön, was eine Elektron ist, wann es sich "bewegt" (oder vielmehr: herumwabbelt) und was es für Eigenzustände gibt (die bei einer Messung beobachtbar ist) und wie es zu Überlagerungen kommt (weil die Summe zweier Lösungen der Schrödingergleichung ebenfalls eine valide Lösung ist)
http://www.imagebanana.com/view/rityc204/4.jpg
Wie gesagt, spiel einfach mit den Programmen herum, man lernt wahnsinnig viel über die Schrödingergleichung, ihre Lösungen und wie sich sich zusammensetzen.
___
Nun also mit diesem ganzen Wissen nochmal zur Frage:
"Bewegen sich Elektronen um Atomkerne?"
Antwort: Nein, auf keinen Fall kreisen sie um den Kern. Es sind "verschmierte" (also nicht-lokale) Objekte, die in den quantisierten Eigenzuständen absolut still stehen. Das einzige was sich "bewegt" sind die realen und imaginären Anteile, die aber nicht beobachtbar sind und nur mathematisch wichtig werden, wenn es zu Superpositionen kommt.
Wird dem System von außen Energie zugeführt, oder gibt das System Energie ab, dann befindet sich das System nicht mehr in einem Eigenzustand, sondern in einer Überlagerung von mehrern Zuständen. Der "Schwerpunkt" des Elektrons scheint sich dann tatsächlich zu bewegen, allerdings trotzdem nicht wie ein klassisches Teilchen. Durch diese Verschiebungen in der Ladungsverteilung kommt es dann zu elektromagnetischen Effekte, über die die Energie abgestrahlt, bzw, aufgenommen wird.
jeremybrood schrieb:Du hast ein naives Verständnis von "statisch", statisch heißt nicht orts- und zeitunabhängig
