SRT, RdG, Uhrenparadoxon was zum Grübeln

mojorisin schrieb:Das ist richtig.

Soll bedeuten: Ich stimme dir zu, dass es sich dabei nicht um eine Uhrensynchronisation handelt.

mojorisin schrieb:Was ist das gewünschte Ergebnis? Soweit ich verstanden habe, dass sich zwei gegeneinder bewegte Uhren nach einer bestimmten Zeit an einem gemeinsamen Ort treffen und dort dann die gleiche Uhrzeit anzeigen.

Im von @nocheinPoet skizzierten Experiment scheitert es bereits daran, dass die Piloten nicht wissen können, wann genau sie 0,6 Ls voneinander entfernt sind:

nocheinPoet schrieb:Dann startet jede mit 0 s wenn die jeweils andere Uhr genau 0,6 Ls entfernt ist

Von daher wäre das gewünschte Ergebnis zunächst einmal, dass beide Uhren bei einer Distanz von 0,6 Ls tatsächlich auf 0 s stehen. Der Rest ist in einer vollständig symmetrischen Situation dann eh trivial.

@Arrakai

Arrakai schrieb:dass die Piloten nicht wissen können, wann genau sie 0,6 Ls voneinander entfernt sind:

Wieso nicht? Theoretisch kann jeder exakt einen Abstand zwischen sich und einem anderen Piloten messen. Sehe da kein Problem.

mojorisin schrieb:Wieso nicht? Theoretisch kann jeder exakt einen Abstand zwischen sich und einem anderen Piloten messen. Sehe da kein Problem.

Naja, ein Vorgehen analog einer Einsteinsynchronisation sollte tatsächlich funktionieren. Für den Uhrenvergleich ist es ja egal, ob die Raumschiffe zueinander ruhen.

Arrakai schrieb:Naja, ein Vorgehen analog einer Einsteinsynchronisation sollte tatsächlich funktionieren. Für den Uhrenvergleich ist es ja egal, ob die Raumschiffe zueinander ruhen.

Nein, so habe ich das nicht gemeint. Es gbit nur dem Piloten eine Handlungsvorgabe wenn er seine Uhr starten soll. Dies bedeutet allerdings nicht, dass aus seiner Sicht die beiden Uhren synchronisiert sind. Wenn beide Piloten die Handlungsvorgabe bekommen bei Erreichen eine bestimmten Distanz zum anderen (z.B. 0.6 LS) die eigene Uhr zu starten, dann sehen sie beim jeweils Anderen das diese Handlung verzögert ausgeführt wird.

Nur im symmetrischen Bezugssystem, d.h. dort wo die Beträge der beiden Geschwindigkeiten gleich sind, nur mit umgekehrten Vorzeichen, werden die beiden Vorgänge (Pilot A starte die Uhr und Pilot B startet die Uhr) gleichzeitig statt finden.

mojorisin schrieb:Nur im symmetrischen Bezugssystem, d.h. dort wo die Beträge der beiden Geschwindigkeiten gleich sind, nur mit umgekehrten Vorzeichen, werden die beiden Vorgänge (Pilot A starte die Uhr und Pilot B startet die Uhr) gleichzeitig statt finden.

Die Bezugssysteme sollen in diesem Fall schon symmetrisch sein, denke ich. Ganz klar ist das nicht, daher habe ich vorsichtshalber "analog einer Einsteinsynchronisation" geschrieben. Analag in dem Sinne, dass natürlich immer die Lichtlaufzeit gemessen werden kann, um den Abstand zu einem bestimmten Zeitpunkt zu ermitteln.

Um ehrlich zu sein verstehe ich bisher nicht wirklich, auf was @nocheinPoet hinaus will. (Die Diskussion mit dem "Spezi" in gleich zwei anderen Foren habe ich zwar gesehen, aber nicht verfolgt.)

Arrakai schrieb:Um ehrlich zu sein verstehe ich bisher nicht wirklich, auf was @nocheinPoet hinaus will. (Die Diskussion mit dem "Spezi" in gleich zwei anderen Foren habe ich zwar gesehen, aber nicht verfolgt.)

@nocheinPoet, ich denke auch es wäre hilfreich wenn du klarer formulieren kannst was denn genua diskutiert werden soll.

@nocheinPoet

nocheinPoet schrieb:Man muss unterscheiden, ob man ein symmetrisches Szenario hat, wie ich es mit den beiden Uhren beschreibe, oder nicht.

Wenn man zwei gegeneinander bewegte Objekte hat, was ist der Unterschied zwischen symmetrischem und unsymetrischem Szenario? Es ist mir nicht klar wie das gemeint ist.

Arrakai schrieb:Nein, geht nicht, zumindest nicht so ohne Weiteres. Wie soll der Pilot entscheiden, wann genau er 0,6 Ls entfernt ist? Im Endeffekt ist genau das die Uhrensynchronisation.

Klar geht das, es ist auch ein Gedankenexperiment, da ist die Methode nicht relevant, selbstverständlich aber kann man feststellen, wie weit man von einem Objekt entfernt ist, oder dieses von einem.

mojorisin schrieb:In den beiden Ruhesystemen der Uhren, starten die Uhren nicht gleichzeitig sind also nicht synchronisiert, wie du schon sagtest.

Doch, in jedem Ruhesystem starten alle Uhren gleichzeitig, ich gebe hier mal die Ereignisse an:


E₀₁ [x₀₁ = − 00,27 Ls; t₀₁ = ± 00,00 s | x'₀₁ = − 00,33 Ls; t'₀₁ = + 00,20 s] ➞ in S bewegte Uhr startet mit 0,20 s
E₀₀ [x₀₀ = ± 00,00 Ls; t₀₀ = ± 00,00 s | x'₀₀ = ± 00,00 Ls; t'₀₀ = ± 00,00 s] ➞ alles auf 0
E₀₂ [x₀₂ = + 00,33 Ls; t₀₂ = ± 00,00 s | x'₀₂ = + 00,42 Ls; t'₀₂ = − 00,25 s] ➞ in S ruhende Uhr startet

Diese drei Ereignisse sind bei t = 0 s in S, bei E₀₁ ist die in S bewegte Uhr, bei E₀₀ der Ursprung beider Systeme, also x, x', t, t' = 0. Und bei E₀₂ ruht die andere Uhr in S.


Drei Ereignisse nach 1 s, gleichzeitig in S:

E₀₃ [x₀₃ = − 00,27 Ls; t₀₃ = + 01,00 s | x'₀₃ = − 01,08 Ls ; t'₀₀ = + 01,45 s]
E₀₄ [x₀₄ = ± 00,00 Ls; t₀₄ = + 01,00 s | x'₀₄ = − 00,75 Ls ; t'₀₄ = + 01,25 s]
E₀₅ [x₀₅ = + 00,33 Ls; t₀₅ = + 01,00 s | x'₀₅ = − 00,33 Ls ; t'₀₅ = + 01,00 s] ➞ beide Uhren treffen zusammen, die in S bewegte Uhr zeigt wie die ruhende Uhr 1,00 s an

Reisedauer in S':

Δt' = t'₀₅ − t'₀₁ = 0,80 s


Die ganze Szenerie nun noch mal aus S' beschrieben:

E₀₆ [x₀₆ = + 00,33 Ls; t₀₆ = + 00,20 s | x'₀₆ = + 00,27 Ls; t'₀₆ = ± 00,00 s] ➞ in S' bewegte Uhr startet mit 0,20 s
E₀₀ [x₀₀ = ± 00,00 Ls; t₀₀ = ± 00,00 s | x'₀₀ = ± 00,00 Ls; t'₀₀ = ± 00,00 s] ➞ alles auf 0
E₀₇ [x₀₇ = − 00,42 Ls; t₀₇ = − 00,25 s | x'₀₇ = − 00,33 Ls; t'₀₇ = ± 00,00 s] ➞ in S' ruhende Uhr startet

Diese drei Ereignisse sind bei t' = 0 s in S', bei E₀₆ ist die in S' bewegte Uhr, bei E₀₀ der Ursprung beider Systeme, also x, x', t, t' = 0. Und bei E₀₇ ruht die andere Uhr in S'.


Drei Ereignisse nach 1 s, gleichzeitig in S':

E₀₈ [x₀₈ = + 01,08 Ls; t₀₈ = + 01,45 s | x'₀₈ = + 00,27 Ls; t'₀₈ = + 01,00 s]
E₀₉ [x₀₉ = + 00,75 Ls; t₀₉ = + 01,25 s | x'₀₉ = ± 00,00 Ls; t'₀₉ = + 01,00 s]
E₀₅ [x₀₅ = + 00,33 Ls; t₀₅ = + 01,00 s | x'₀₅ = − 00,33 Ls; t'₀₅ = + 01,00 s] ➞ beide Uhren treffen zusammen, die in S' bewegte Uhr zeigt wie die ruhende Uhr 1,00 s an

Reisedauer in S:

Δt = t₀₅ − t₀₆ = 0,80 s


E₀₀ ist das Ereignis in beiden Systemen, an dem die Uhren synchronisiert werden, ...

@mojorisin

Eventuell helfen ja die Ereignisse weiter. Mir geht es um den Unterschied zwischen dem klassischen Zwillingsparadoxon und dem Uhrenparadoxon, so wie ich es beschrieben habe.

Beim Zwillingsparadoxon bewegt sich ein Objekt (Uhr) eben über eine gegebene Strecke an beiden Enden auch je eine Uhr. Wobei Uhren als Objekte nicht nötig sind, sie zeigen ja eh nur die Ortszeit an, man kann einfach alles aus der Raumzeit schneiden, sind nur Ereignisse, Punkte eben.

Damit wir mal Werte für das alte Beispiel haben, Rakete H fliegt von der Erde über 18,14 Ls zum Mond mit 0,672 c. Werte sind etwas gerundet, die Uhr in der Rakete zählt 20 s hoch, die auf der Erde und dem Mond 27 s. Als H auf Höhe der Erde ist, werden die Uhren gestartet.

Wir haben also klassisch eine Uhr die bewegt in S "langsamer" läuft und 20 s < 27 s.

Nun wurde fälschlich behauptet, man könnte die Uhren ja auch beim Mond synchronisieren, und dann würden sich beide Zeiten vertauschen, weil das ja symmetrisch sei. Ist natürlich falsch, will man zeigen, dass in S' auch die nun dort bewegte Uhr auf dem Mond (und der Erde) langsamer läuft, als die in er Rakete, welche ja 20 s zählt, reicht es schon aus die 20 s mit γ⁻¹ zu multiplizieren und dann bekommt man so eben 14,81 s. Da die Uhr auf dem Mond nun aber 27 s anzeigt, bedeutet es, sie muss eben mit + 12,19 s gestartet sein.

Kann das auch alles noch mal im Minkowski-Diagramm zeigen.

So weit so gut, das Beispiel eben ist nicht symmetrisch, wir haben die Ruhelänge von Erde/Mond ist S mit 18,14 Ls und die ist in S' auf 13,44 Ls kontrahiert. Man kann also die Zeiten nicht einfach umdrehen. Darüber hinaus wurde noch behauptet, man könnte durch das Beobachten von Uhren feststellen, ob man selber gegenüber dem Mond oder der Mond gegenüber einem bewegt sei, als das Relativitätsprinzip widerlegen. Ja schon recht abgedreht.

Im Lauf der Debatte wurde nun ein voll symmetrisches Beispiel geschraubt und aus dem habe ich hier nun das mit der 1 s gezimmert.

Und ich kann die Gleichung gerne zeigen, dachte aber es ist was zum Grübeln, denn so wie ich es sehe ist es schon interessant die Werte der Orte so zu finden, dass man am Ende auf beiden Uhren gleiche Zeiten hat.

nocheinPoet schrieb:Doch, in jedem Ruhesystem starten alle Uhren gleichzeitig,

Ich habe noch Nachfragen um Missverständnissen vorzubeugen:

Es gibt genau drei Ereignisse:

• Ereignis 1: Uhr 1 startet
  
• Ereignis 2: Uhr 2 startet
  
• Ereignis 3: Beide Uhren treffen sich.
  

Dabei bewegen sich Uhr 1 und Uhr 2 aufeinande zu. Richtig soweit?

@mojorisin

Ja, aber die ersten beiden Ereignisse sind nicht gleich wenn ich das System wechsel. Also man baut es auf, sucht sich ein System, dort starten die Uhren gleichzeitig mit 0 s und dann treffen sie zusammen und zeigen beide 1 s an.

Wechselt man das System, können diese ersten beiden Ereignisse dort ja nicht auch gleichzeitig sein, wegen der RdG, dort hat man dann zwei andere Ereignisse, die gleichzeitig dort mit 0 s die beiden Uhren starten.

nocheinPoet schrieb:Ja,

Gut.

nocheinPoet schrieb:sucht sich ein System,

Das System in dem die beiden Ereignisse "Uhr starten" gleichzeitig stattfinden ist automatisch das System in dem die Betraege der Geschwindigkeiten gleich gross und entgegengerichtet sind oder einfgach gesagt: Ein Beobachter in der Mitte der beide Uhren mit gleicher Geschwindigkeit auf sich zukommen sieht, eine von links die andere von rechts, und sich beide Uhren dann beim Beobachter treffen.

Was mit jetzt aber nicht klar ist, was genau diskutiert weden soll? Was ist genau das Problem?

mojorisin schrieb:Das System in dem die beiden Ereignisse "Uhr starten" gleichzeitig stattfinden ist automatisch das System in dem die Beträge der Geschwindigkeiten gleich groß und entgegen gerichtet sind oder einfach gesagt: Ein Beobachter in der Mitte der beide Uhren mit gleicher Geschwindigkeit auf sich zukommen sieht, eine von links die andere von rechts, und sich beide Uhren dann beim Beobachter treffen.

Nicht wirklich, sicher kann man ein drittes System so definieren, dass sich beide Uhren darin gleicher Geschwindigkeit entgegen gerichtet bewegen, habe ich aber nicht.

Der Hintergrund ist nicht in ein paar Worten geschrieben, ging um eine Diskussion zur Zeitdilatation, dem Zwillingsparadoxon, dann dem Uhrenparadoxon, dann kam ein Crank und meinte er könnte durch das Beobachten einer Uhr in einem Zug welche sich vor und zurück bewegt die SRT widerlegen, dann kam ein anderer User und erklärte, der Crank irrt, aber wenn man aus dem Fenster des Zuges schaut, könnte man durch das Beobachten der Uhren die am Fenster vorbeiziehen unterscheiden, ob man selber oder eben die Uhren vor dem Fenster wirklich bewegt sind.

Dafür stützte und verwies er auf das Video von Peter Kroll, wo der eine fiktive Reise von der Erde zu Alpha Centauri mit 0,8 c in 3 Jahren beschreibt, während auf der Erde und Centauri 5 Jahre vergehen sollen. Aus dem Fenster des Raumschiffes werden nun Uhren beobachtet, und die laufen anscheinend schneller als die Borduhr, denn die zählen ja in nur 3 Jahren eben 5 Jahre rauf. Peter zeigt das im Video so ab 602 s.

Der User ist nun im Glauben gefangen, seine Borduhr würde die sein, die wirklich dilatiert, die an denen er vorbeifliegt die dilatieren nicht, die gehen ja schneller, was beweist, er sei mit der Rakete der wirklich bewegte, denn sonst müssten die Uhren an denen er vorbeifliegt ja langsamer und nicht schneller als die Borduhr laufen.

Er konstruierte darauf ein Szenario, in dem die Rakete von der Erde zum Mond fliegt und das mit 0,672 c in 27 s über 18,14 Ls, die 27 s wurde die Uhr auf dem Mond hochzählen und die an Bord der Rakete hingegen nur 20 s. Würde man das aber nun "umdrehen", Erde und Mond wären gegenüber der Rakete bewegt und die Rakete ruhend, würde die Uhr in der Rakete die 27 s anzeigen und die auf dem Mond nur 20.

Darauf erklärt ich, dass das im Widerspruch zum Relativitätsprinzip steht, man natürlich keine solche Fallunterscheidung machen kann und das die Uhren - auch im Beispiel von Peter - natürlich bewegt dilatiert laufen. Das die Uhren am Fenster der Rakete im Beispiel von Peter, im Video hingegen schneller zu laufen scheinen, als die an Bord würde an der RdG liegen, die Uhren gehen eben immer weiter auch ein Stück vor, einzeln betrachtet würde aber jede bewegt gegenüber dem Raumschiff dennoch dilatiert laufen.

Das wurde endlos bestritten, es gab einen längeren Disput, im Laufe dessen wurde ein weiteres Szenario entwickelt, in dem zwei gleich lange Züge (ich übertrage die Szene mal auf zwei Züge) mit einer Ruhelänge von 18,14 Ls aneinander mit 0,672 c vorbeifliegen, die Uhren in den Zügen starten, wenn die beiden Loks sich bei t, t', x, x' = 0 treffen.

Am Ende treffen dann noch beide Enden der beiden Züge aufeinander, die beiden Uhren dort zeigen dann beide gleiche Werte.

Das war die Story, kürzer konnte ich nicht. :D

Dazu wurden dann zwei Minkowski-Diagramme für S und S' erstellt und mir viel eine Symmetrie auf, ich betrachte nun mal nur beide Uhren hinten im Zug, jede Uhr muss sich über die Ruhelänge des eigenen Zuges plus der kontrahierten Länge des anderen Zuges bewegen und somit bewegen sich beide über die gleiche Streckenlänge.

Alle Uhren werden auch mit dem Treffen der beiden Loks gestartet. Normal hat man in so einem Beispiel ja nicht gleiche Werte auf der Anzeige der Uhren die sich treffen.

Nun dann habe ich mir eine Gleichung gebastelt, um bei beliebigen Abstand und Geschwindigkeit immer gleiche Zeiten auf den Uhren zu bekommen, dazu muss ich den Ort der hinteren Uhr berechnen.

v = 0,6 c
γ = 1,25

Δx = x₀₁ – x₀₂ = 0,6 Ls

x₀₂ = Δxγ / (γ +1) = 0,33 Ls
x₀₁ = + x₀₂ – Δx = - 0,27 Ls

Die Gleichung die ich hier meine ist die für x₀₂, man kann so für jeden Abstand bei jeder Geschwindigkeit eben die passenden Orte so finden, dass die Uhren beim Treffen dann denselben Wert zeigen. Und nein es hat nicht wirklich einen großen Nährwert.

---

mojorisin schrieb:Was mit jetzt aber nicht klar ist, was genau diskutiert werden soll? Was ist genau das Problem?

Es gibt kein Problem, nicht wirklich, und diskutieren kann man die Relativität der Gleichzeitigkeit, konkret wie Lorentzkontraktion und Zeitdilatation zusammenhängen.

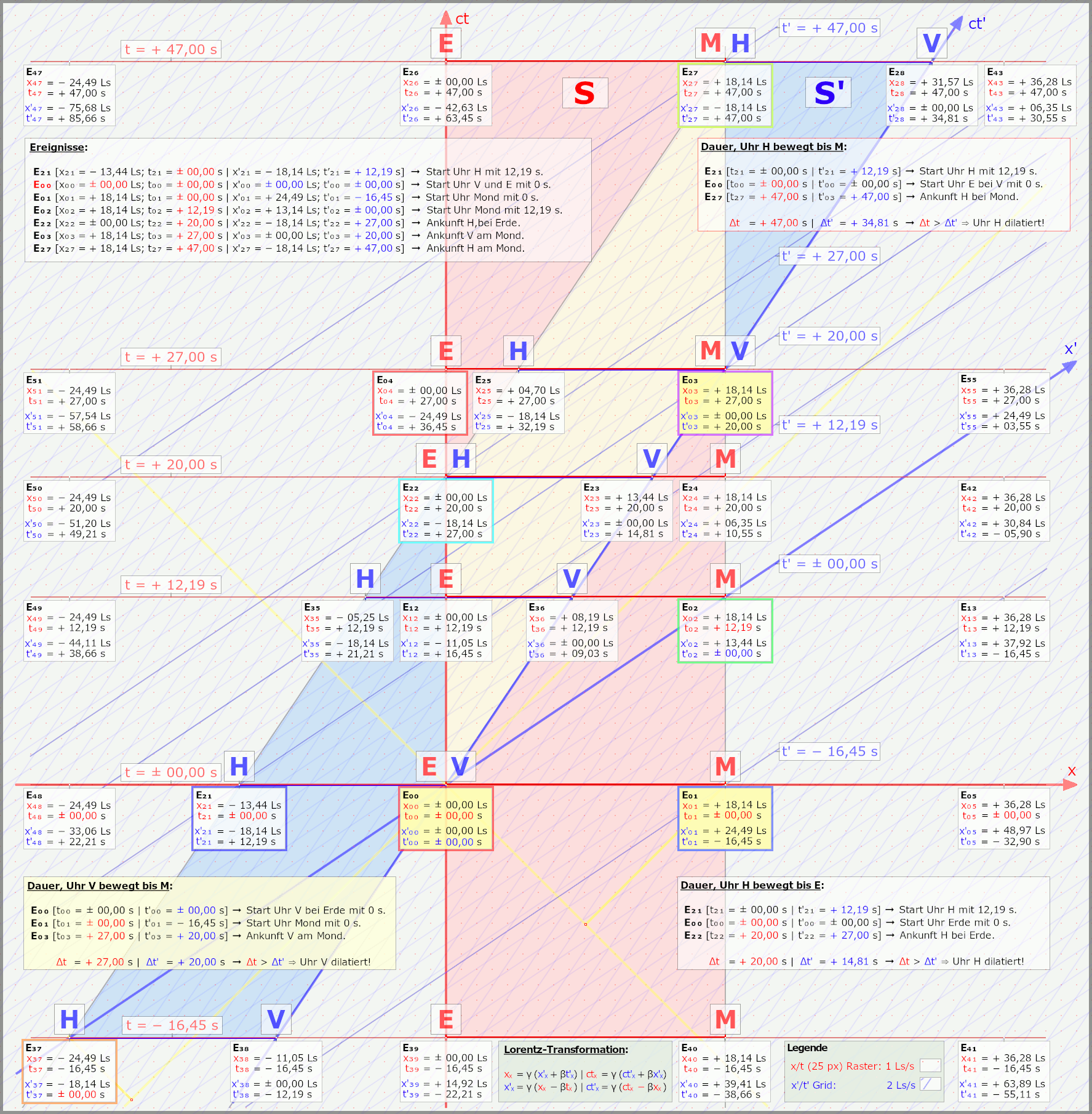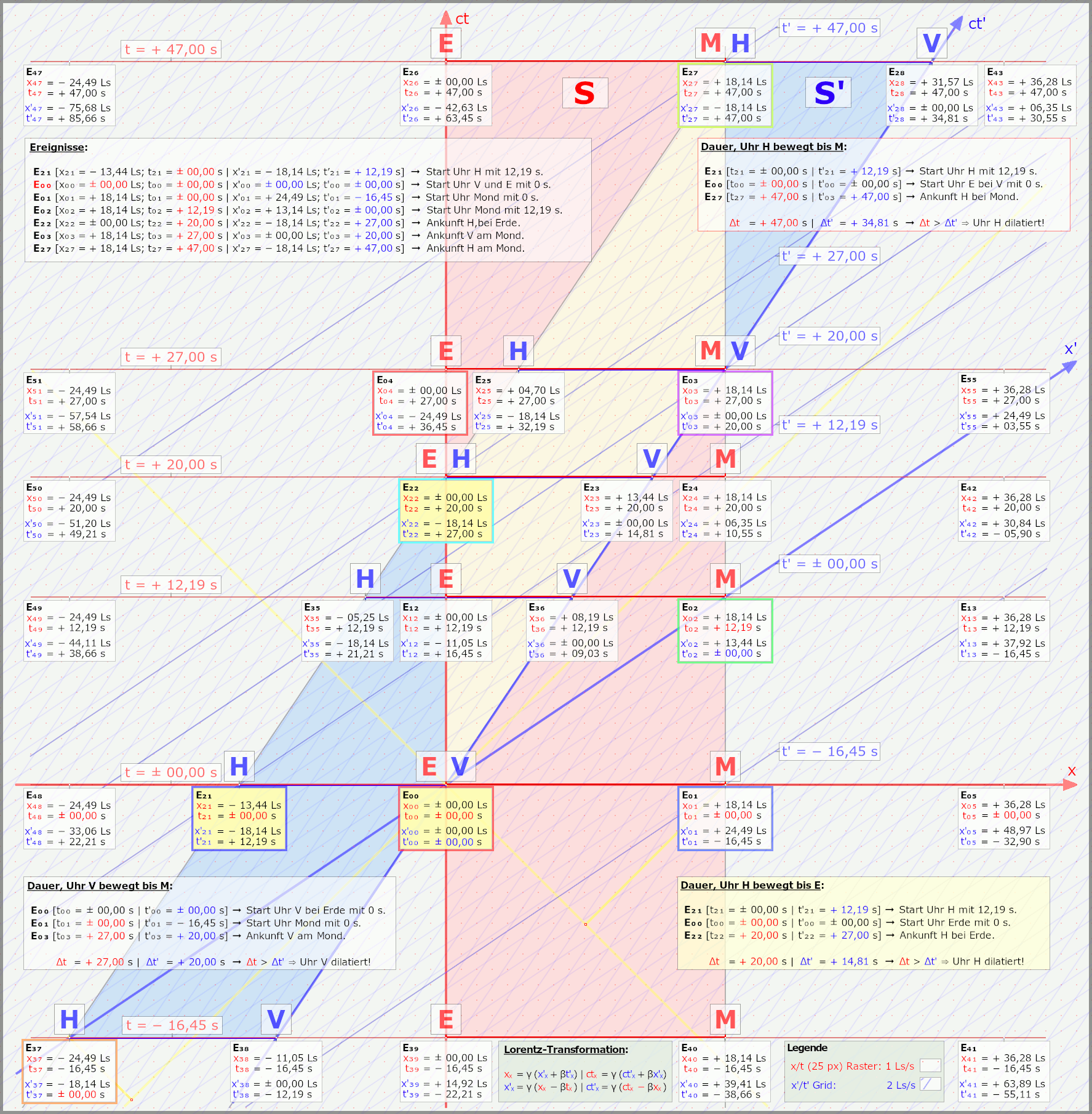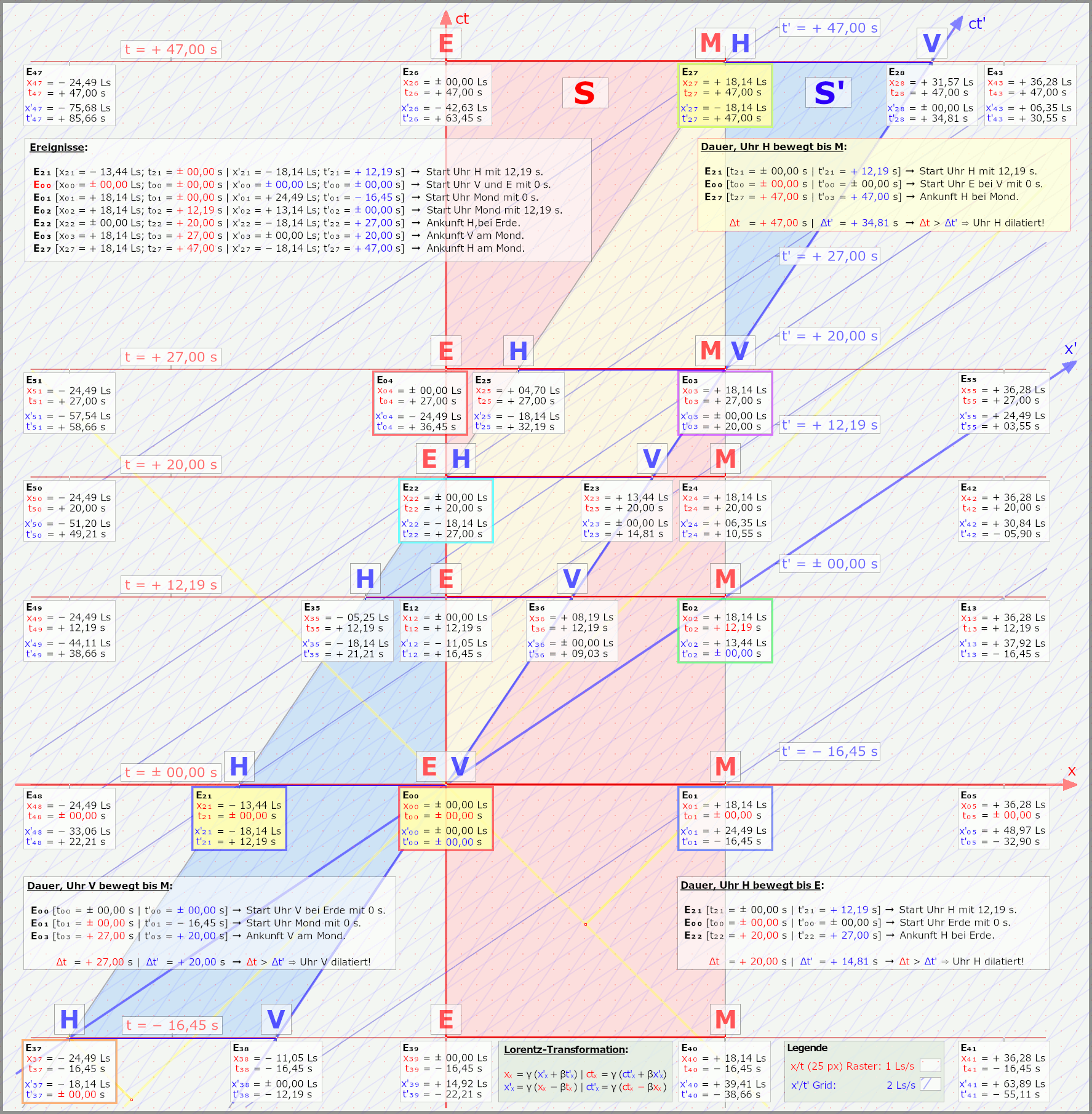
Kann da die Szene von Peter nehmen oder das mit der Reise zum Mond, gehen wir zum Ereignis bei der Erde, wo die Uhren im Raumschiff und der Erde mit 0 s starten, bei x, x' = 0. In S dem Ruhesystem von Erde und Mond ist der Mond 18,14 Ls (dieser Wert ergibt sich aus der Vorgabe von 20 s zu 27 s, schon klar das der Mond nicht so weit weg ist) von der Erde entfernt, auch da startet die Uhr mit 0 s als die Rakete auf Höhe der Erde ist.

Betrachten wir das nun aus S' dem Ruhesystem der Rakete, ist der Mond hingegen nur 13,44 Ls weiter entfernt, da Erde/Mond bewegt und die 18,14 Ls eben kontrahiert sind. Ja alles sicher bekannt und kalter Kaffee. Aber das Ereignis auf dem Mond in S' in 13,44 Ls Entfernung vom Raumschiff hat 12,19 s auf der Uhr, durch die RdG geht die Uhr in S' eben vor. Nun hüpft man im Gedanken mal zum Mond eben dort zum Zeitpunkt von 12,19 s, einem gegenüber ist eine in S' ruhende Uhr die 0 s anzeigt.

Jetzt unterhalten sich der Beobachter auf dem Mond und der bei der Uhr gegenüber dem Mond, für den in S' startet ja gerade seine Uhr und die im Raumschiff in 13,44 Ls Entfernung bei der Erde mit 0 s, für den auf dem Mond liegt das Treffen bei der Erde aber schon 12,19 s zurück, für den Beobachter dort ist das Raumschiff schon an der Erde vorbei.

Gut, viel Text, sollte dennoch wenig sein, glaube nicht, dass Du nun wirklich mehr Durchblick hast. :D

Aber egal, Thema ist ja dennoch immer wieder spannend, konkret frage ich mich nun, wenn der fiktive Beobachter in S' beim Start seiner Uhr am Mond mit 0 s und die auf dem Mond 12,19 s anzeigt, dann blickt der in S' ja im Grunde in die Zukunft von S. Er könnte ja nun ein Foto der Monduhr mit 12,19 s machen und dann stoppt man das Raumschiff.

Damit fällt die RdG wieder raus, er hat aber ein Foto aus der Zukunft auf dem Mond, er wird das sicherlich nicht in 12,19 s dort vor Ort zeigen können, wegen der Kausalität, aber dennoch wäre es doch die Zukunft, die müsste dann doch voll determiniert sein.

Also so weit mal eben vor dem Wochenende, wollte das nicht offen lassen, hast viel Text, eventuell findest Du ja was ...

@nocheinPoet
Mal so als Laie gefragt, geht es darum, davon zu überzeugen dass es sich "lediglich" und faktisch um zwei gleichberechtigte Beobachter des jeweiligen Systems handelt?

nocheinPoet schrieb:Der User ist nun im Glauben gefangen, seine Borduhr würde die sein, die wirklich dilatiert, die an denen er vorbeifliegt die dilatieren nicht, die gehen ja schneller, was beweist, er sei mit der Rakete der wirklich bewegte, denn sonst müssten die Uhren an denen er vorbeifliegt ja langsamer und nicht schneller als die Borduhr laufen.

Sollte er das so geschrieben haben - ich habe es wie gesagt nicht näher verfolgt -, dann irrt er sich in der Tat. Ich glaube auch, dass ich mit deiner Begründung konform gehe, bin mit aber nicht ganz sicher. Daher:

Man stelle sich eine Reihe von Uhren vor, die zwischen der ersten und der letzten Uhr geradlinig aufgereiht sind und relativ zur ersten und letzten Uhr ruhen. Alle diese Uhren bilden gemeinsam ein Inertialsystem S. Die Uhr in der Rakete ist kein Teil dieses Inertialsystems, da sie sich relativ zu den anderen Uhren bewegt, und zwar mit gleichförmiger Geschwindigkeit genau geradlinig an allen Uhren vorbei. Sie befindet sich in ihrem eigenen Inertialsystem S'. Jetzt vergleicht die Uhr (Beobachter) in der Rakete bei jeder der aufgereihten Uhren die Zeiten (jeweils die eigene Zeit mit der, die die Uhr vor Ort anzeigt). Und wird feststellen, dass jede einzelne Uhr etwas schneller gelaufen ist als sie selbst. Die letzte Uhr (am Ziel) wird dann am schnellsten gelaufen sein (sie "rast" aber nicht am Ende wie wild, sondern sie wird halt nur am Ende verglichen).

Das liegt tatsächlich an der Relativität der Gleichzeitigkeit. Es wurden alle Uhren in S synchronisiert, aber eben nicht in S'. Die grüne Uhr war in S' von Anfang an nicht korrekt mit der letzten Uhr synchronisiert (das gilt auch für alle anderen Uhren auf dem Weg). Eben das ist es, was aus Sicht der Uhr in der Rakete dann dafür sorgt, dass alle Uhren auf dem Weg schneller laufen (und zwar jede einzelne davon noch ein Wenig schneller als die vorherige). Und das, obwohl die Zeitdilatation an sich symmetrisch ist, d.h. die Symmetrie zwischen der bewegten Uhr und jeder einzelnen Uhr auf dem Weg erhalten bleibt (im direkten 1:1-Vergleich). Man muss halt nur die Desynchronisation der Uhren berücksichtigen, dann ergibt sich der Rest von selbst.

Passt so auch aus deiner Sicht?

@nocheinPoet

nocheinPoet schrieb:Der User ist nun im Glauben gefangen, seine Borduhr würde die sein, die wirklich dilatiert, die an denen er vorbeifliegt die dilatieren nicht, die gehen ja schneller, was beweist, er sei mit der Rakete der wirklich bewegte, denn sonst müssten die Uhren an denen er vorbeifliegt ja langsamer und nicht schneller als die Borduhr laufen.

Ist halt nicht so. Wenn das jemand nicht versteht, kann man dann halt nichts machen.

nocheinPoet schrieb:Doch, in jedem Ruhesystem starten alle Uhren gleichzeitig, ich gebe hier mal die Ereignisse an:

Ich wuerde dir ein komplett anderes Format vorschlagen:


(Achtung: Zahlen nur symbolisch nicht masstabsgetreu!!!)
Man sieht im oberen Teil die Minkowski-Diagramme inklusive der drei Eregnisse. E1 ist wenn Uhr 1 startet, E2 wenn Uhr 2 startet, E3 wenn sich die Uhren treffen. das ungestrichene System is das Schwerpunktsssytem (der Geschwindigkeiten), sprich beide Uhren bewegen sich mit derseleben Geschwindigkeit aufeinande zu.

Im unteren Teil sieht man die Daten der Koordinaten. Die Tabelle zeigt die Koordinaten der drei Eregnisse aus den jeweiligen Inertialsystemen an. Im System S sieht man die Uhren synchronisiert starten (Startzeit von E1 und E2 is gleich) und die Synchronisation bleibt beibehalten. In den jeweiligen Eigensystem der Uhren ist das nicht der Fall (Startzeit von E1 und E2 is ungleich und jeweils negativ fuer die andere Uhr). Dort startet die jeweils andere Uhr verfrueht.

Bei E3 zeigen die beiden Uhren die gleiche Zeit an.

Arrakai schrieb:Passt so auch aus deiner Sicht?

Ja passt voll und ganz.

@mojorisin

Ja sieht nett aus, ich mag wenn es symmetrisch ist. Aber wie auch immer, es ist ja gewachsen, wenn ich die beiden Digramme hier aus der Diskussion zeige, wird es sicher den Thread erschlagen ...






Es geht hier um H und M, in beiden Diagrammen oben treffen sich H und M(ond) dann mit 47 s auf der Uhr.