Die Paradoxa des Wahrscheinlichkeitsidioten und weitere Rätsel

@bgeoweh
okay, so weit hab ich natürlich nicht gerechnet. Dachte nur, da die Strecke pro Stunde ja immer kürzer wird. Und dann hab ich nur geschätzt.

Er hat zwar unendlich viel Zeit, aber die kürzeste Länge ist doch die Planck-Länge, oder nicht? Also kann er ja auch nicht unendlich weit kommen.

skagerak schrieb:Dachte nur, da die Strecke pro Stunde ja immer kürzer wird.

Tja, Unendlichkeit ist tricky :D Die Strecke wird immer kürzer, aber die Strecke wird langsamer kürzer, als die Stunden mehr werden :D

skagerak schrieb:Er hat zwar unendlich viel Zeit, aber die kürzeste Länge ist doch die Planck-Länge, oder nicht? Also kann er ja auch nicht unendlich weit kommen.

Das ist Physik, das hat mit der reinen Mathematik nichts zu tun ;)

bgeoweh schrieb:Die Strecke wird immer kürzer, aber die Strecke wird langsamer kürzer, als die Stunden mehr werden

Ebendrum.

Das ist Physik, das hat mit der reinen Mathematik nichts zu tun

Joa, aber Dein Ergebnis klingt viel zu einfach. Angenommen er kommt immer pro Stunde 1 km. Denn kommt er ja auch unendlich weit bei unendlich viel Zeit. Aber in dem Fall wird die Strecke ja immer kürzer. Paradox halt :)

skagerak schrieb:Aber in dem Fall wird die Strecke ja immer kürzer. Paradox halt

Da ist nichts paradox, es sieht nur so aus. Mathematisch gesagt: bei den bekannten Beispielen konvergiert die Summe (zu einem Grenzwert), wie es z.B. der Fall wäre, wenn sich seine stündliche Geschwindigkeit immer halbieren würde - hier divergiert die Summe, es gibt keinen Grenzwert. Das kann man z.B. auch daran sehen, dass man sich jeden beliebigen Startpunkt (also z.B. nach fünf Stunden) rausnehmen kann und auch ab dort noch beliebig weit kommt.

@bgeoweh
Sorry, bin nur Laie, verstehe also nicht genau was Du meinst. Also muss man ja noch nicht mal rechnen wenn man weiß dass er unendlich viel Zeit hat, da dies ja anscheinend auch bedeutet dass er so oder so auch unendlich weit kommt.

Ich werf mal das in den Ring.

Wir haben 1/2, 1/4 usw, doch Schema bleibt.

@skagerak
Wenn er wie folgt gehen würde:

1 + 1/2 + 1/4 + 1/8 ...

Würde er nicht unendlich weit kommen, trotz unendlich langer Zeit. Die Reihe konvergiert gegen einen Wert (in dem Fall 2).

Bei der Reihe von @mojorisin ist es anders. Sie divergiert.

Ob eine Reihe konvergiert oder divergiert kann man auf viele Arten feststellen (und ich kenne mich mit keiner aus :D )

Versuch mal @bgeoweh 's Ansatz auf die konvergierende Folge anzuwenden. Es funktioniert nicht. Du siehst, die unendlich lange Zeit alleine reicht nicht.

wuec schrieb:Wir haben 1/2, 1/4 usw, doch Schema bleibt.

Es ist hier ein eklatanter Unterschied, ob der Nenner exponentiell abnimmt wie in deinem Beispiel oder nicht. Das Schema bleibt eben nicht!

@bgeoweh
Nur der Startwert ist ein anderer. Laufindex und Funktion nicht.

@wuec
Nein. Bei deinem Beispiel handelt es sich um eine geometrische Reihe. Bei der Aufgabe von @mojorisin nicht.
@bgeoweh hat recht.

wuec schrieb:Laufindex und Funktion nicht.

Doch.

Dein Bildchen ist Summe

die Funktion von mojorisin ist Summe

@bgeoweh
@Izaya
Sorry, aber denn komme ich eben nicht mit, hab´s aber versucht ;)
Wenn das Ergebnis so sein soll, denn isses eben so, auch wenn es mir nicht ganz einleuchtet und schlüssig klingt :)

Kann mit den Begriffen Konvergenz und Divergenz nichts anfangen.

Eine Reihe (bzw. Summenfolge) konvergiert (erreicht bei "unendlich viel Zeit" einen diskreten Wert), wenn Folgeglieder sich beliebig nahe kommen können. Was bedeutet das?

Der Unterschied, nach der Addition des nächsten Glieds wird quasi unendlich gering. Das macht Sinn, denn wenn wir endgültig einen Wert erreichen wollen, dürfen wir nicht immer wieder etwas merklich hinzufügen.

Also, beweisen wir einfach, dass bei der vorliegenden Reihe die Folgeglieder sich eben nicht beliebig nahe kommen können.

Jetzt kommt die dunkle Magie, bei der ich mir den passenden Ansatz aus dem Hut ziehe.

Wir betrachten den Abstand vom n-ten Glied bis zum 2n_ten Glied:



Und reicht es, zu beweisen, dass es einen Mindestwert für den Abstand gibt. Wir schätzen also einfach den unteren Wert ab. Dafür ersetzen wir alle Brüche durch den letzten 1/2n, welcher den geringsten Wert hat.
Dann haben wir den Bruch \frac{1}{2n} und den haben wir n mal.
Würden wir beispielsweise 5 für n einsetzen, kämen wir zu:


Die Summe ist also, wenn wir wieder zur Schreibweise mit n zurückkehren, äquivalent zu:

Daraus folgt, es gibt einen Mindestabstand größer 0.

Folgeglieder können sich also nicht beliebig nahe kommen, wie es für eine Konvergenz notwendig wäre. Die Reihe divergiert also. Bei unendlich viel Zeit kommt Unendlich als Ergebnis raus.

Somit haben wir (wenn ich nicht zu viele Fehler gemacht habe), das Cauchy-Kriterium angewandt.
Nichts zu ernst nehmen. Ich habe keine Ahnung von Reihen.

Damit kann man auch beweisen, dass die Folge von @wuec konvergiert. aber den Beweis jetzt auch noch aufzuschreiben, würde meinen inneren Schweinehund mehr quälen, als er verdient hat :troll:
Kann man sich hier anschauen: https://de.wikibooks.org/wiki/Mathe_f%C3%BCr_Nicht-Freaks:_Cauchy-Kriterium_f%C3%BCr_Reihen#Anker:Konvergenzaufgabe

Oder man nutzt die Idee von @bgeoweh anstelle eines rigorosen mathematischen Beweises.
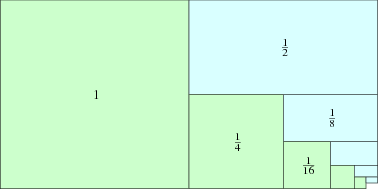
Erster Schritt: 1
Zweiter Schritt: 1/2 + 1/4 + 1/5 + 1/6 + ... < 1
Man kriegt den zweiten Schritt nicht richtig hin (kommt nicht über 1), geschweige den noch mehr. Also konvergiert die Reihe gegen einen Wert.

---

wuec schrieb:Nur der Startwert ist ein anderer

Es ist derselbe Startwert. 1. Nur so nebenbei.

Jopp. Aufgabe falsch gelesen, über Nacht vergessen oder altersbedingte Degeneration.
Ich hatte mich auf den ollen Zenon eingeschossen und freute mich wie blöd, dass ich mich noch an meine jungen Jahre erinnern konnte.
Egal. Wieder ein Grund mich sinnlos zu besaufen.

@wuec
Die Erzählung spielt auf Zenons Paradoxon an:

mojorisin schrieb:Nachdem Achilles nach der Rennen mit der Schildkröte heimgeht

Wahrscheinlich daher. :)

Vermutlich. So ein Lump, der Aufgabenkryptiker.

@Izaya
Sorry, aber das ist mir einfach zu hoch so erklärt. Falls die Mühe für mich war, besten Dank trotzdem :)

Ich versuche es logisch zu betrachten, und dann leuchtet es mir schon ein dass die Strecke dann auch unendlich sein muss. Aber irgendwie auch nicht. Je länger die Zeit, desto kürzer die zu addierende zurückgelegte Strecke....naja, also unendlich null komma .... arrrrgh, ich raffs einfach nicht.

Deswegen habe ich Mathe immer gehasst, ich kann der Logik einfach nicht folgen bei bestimmten Dingen.

@Izaya
Vielleicht lasse ich mich auch einfach nur zu sehr beeinflussen von der Formulierung der Frage

Wie weit kommt Achilles wenn sein Tempo in diesem Maß weiter nachlässt, er aber unendlich lange Zeit weiter laufen kann?

Das klingt so als wenn es eine bestimmte Strecke, also eine Grenze gäbe.

@Izaya

skagerak schrieb:Das klingt so als wenn es eine bestimmte Strecke, also eine Grenze gäbe.

Ja das ist das bösartige daran ;-)

Ich habe die Aufgabe von hier:

https://books.google.de/books?id=-5ioCgAAQBAJ&pg=PA233&lpg=PA233&dq=arens+mathematik+die+idee+der+reihen&source=bl&ots=epScUAxLTK&sig=5lUrrdkf_IcTDtNMUCneNxKtQGQ&hl=de&sa=X&ved=2ahUKEwi1wYOh7-jfAhV5AxAIHZtRDgAQ6AEwDXoECAIQAQ#v=onepage&q=arens%20mathematik%20die%20idee%20der%20reihen&f=false

Arens - Mathematik (Aufgabenstellung in der EInleitung zum Kapitel 8)

Die Aufgabe ,die ich hier eingestellt habe, bildet die sogenannte harmonische Reihe. Interessant daran ist, dass obwohl die Summanden eine Nullfolge bilden (höhere Summanden gehen immer mehr gegen Null), divergiert die Reihe (strebt nicht gegen einen bestimmten Wert sondern geht gegen unendlich.)

Für mich war das interessante daran, das eigentlich das Paradoxon von Achilles sehr bekannt ist (Dort behandelt man eine geometrische Reihe). Dort versteht man oder lernt an das eine unendliche Reihe auch eine endliche Summe haben kann (gilt für nicht für alle geometrischen Reihen!). Das erscheint einem nach einer kurzen Überlegung recht logisch, und ich habe das dann in meiner gnadenlosen Weisheit direkt auch auf diese Aufgabe angewandt, und ordentlich auf de Schnauze gefallen.

Zur Summe der harmonischen Reihe:
Man kann beweisen, dass die Summe von 1+1/2+1/3+ ...+1/n ungefähr gleich ln n ist (genauer ln n + Euler-Mascheroni Konstante, etwa 0,577) ln ist der Natürliche Logarithmus.
Um also eine Summe größer als x zu erreichen muss man "nur" e hoch x Glieder addieren. Die englische wiki hat dafür ein Beispiel:
the sum of the first 10 hoch 43 terms is less than 100