Auftriebskraftwerk

Thorsteen schrieb:Dann würde die Tonne trotz der 200 Kg Auftrieb am Grund bleiben

Hallo Thorsteen,
falsch verstanden und richtige Schlußfolgerung 😀😀😀
Das Fass würde am Grund bleiben.
Poipoi hat es kurz und gut erklärt.
Meine Ergänzung wird etwas länger...

Also nach der Kräftebilanz schauen. Dafür sind die
Vertikalkomponenten interessant.

Im Fall des Fasses am Grund :
senkende Komponente ist der Druck auf die obere Stirnfläche
hebende Komponente mangels Druck auf die untere Stirnfläche Null
-->das Fass wird auf den Grund gedrückt.

Ich hoffe das war jetzt nicht zu langatmig.

Noch kleine Ergänzung :
Auftrieb ist also nur wirksam wenn mindestens die untere Fläche
mit Druck beaufschlagt ist (Körper schwimmt an der Oberfläche)
und erhöht sich je weiter der Körper eintaucht.
Ist der Körper komplett eingetaucht, hat der Auftrieb sein
Maximum erreicht. Es ist keine weitere Steigerung des Auftriebs
möglich.

Pflaume schrieb:Ich hoffe das war jetzt nicht zu langatmig.

Ist immer noch viel zu lang :D

Im Grunde genügt nur ein Wort: Klospülung

@Thorsteen: Es ist am Besten, sich von der Vorstellung, dass Auftrieb durch Volumen ensteht, ganz zu lösen. Auftrieb entsteht ausschliesslich durch Druck auf Flächen. Das Volumen ist lediglich nützlich, um im Standardfall den Betrag des Auftriebs zu berechnen.

Ein anschauliches Beispiel wäre ein luftgefüllter Zylinder, den man von unten abgedichtet in einen Wasserbehälter einführt. Obwohl sich sein Volumen (bzw. ein Teil davon) im Wasser befindet, erfährt er keinen Auftrieb, sondern im Gegenteil eine Kraft nach unten.

Peter0167 schrieb:Im Grunde genügt nur ein Wort: Klospülung

😀😀
Um das zu sehen muss man aber den Deckel heben
( und hoffen dass es kein Plumpsklo ist 😀)

Ausserdem hätte Thorsteen vermutlich komisch gekuckt
wenn ich ihm nur “Klospülung“ hingeschmissen hätte. 😀

Das Phänomen Auftrieb ist in allen seinen Einzelheiten schon ziemlich spannend und interessant. Im Wesentlichen dadurch, dass es unserer Alltagserfahrung scheinbar entgegenläuft. Es ist Gravitation "umgekehrt". Was zB auch viele nicht so ohne Weiteres auf dem Schirm haben, ist die Tatsache, dass alles was auf dem Grunde des Luftmeeres rumliegt (also auf der Erdoberfläche) ebenfalls einen Auftrieb erfährt.

Es ist übrigens eine Antwort gekommen.

SpoilerHallo Forum
Zugegeben, die Richtigkeit und die Bildliche Darstellung sowie Auslegung der Auftriebskraft hat
bewirkt das ich zum ersten mal den Auftriebsbereich Aufarbeite. Das Einfache Denken resultiert
auf dem Messverfahren der Versuchsanlage in der zwischen dem Kolben 14 der Kraftübertragung
und der Zylindersäule eine Hydraulische Waage ist die im stillstand und im Arbeitshub die wirkende Kraft einschließlich der Reibung immer Anzeigt. Einfachhalber lehne ich mich an Ihre Darstellung
Seite 2550 am 03.01.2018 0,7:29 an, der aktivierten 3-Kammer Säule. wir nehmen an, der Zylinder 1. befindet sich in der Schleusen Öffnung ohne der Zylinder Säule. Die Ventile der Zylinder Kammern a und b sind Geschlossen mit einer Restflüssigkeit 1cm. Der Schweredruck der Vorrichtung wirkt
mit 9,t auf den Zylinder und erhöht der Druck in den Kammern nach der Gleichung
p = Kraft 9.000 kg : Kolbenflächen 20.000 cm2 = 4.5 at, das bewirkt eine Kraft auf den Kolben 14
der Kraftübertragung s Anlage = 9t. Die steigende Reaktionskraft wirkt mit 9t nach oben und das
Kräfte Ergebnis im Heben Hub = 0. die übrige Zylindersäule Gewichtskraft - Auftrieb.

Poipoi schrieb:Es ist übrigens eine Antwort gekommen.

Whow, hört sich ja richtig ergebnissoffen an.
Bin mal gespannt wann der Rückfall in alte Stereotype kommt (seufz).

uatu schrieb:Es ist am Besten, sich von der Vorstellung, dass Auftrieb durch Volumen ensteht, ganz zu lösen. Auftrieb entsteht ausschliessich durch Druck auf Flächen. Das Volumen ist lediglich nützlich, um im Standardfall den Betrag des Auftriebs zu berechnen.

Bin auch noch leicht verunsichert:



1) = kein Auftrieb.
2) und 3) auch kein Auftrieb oder doch?

@delta.m

2) und 3) haben Auftrieb.

einen Pfeil hab' ich vergessen bei 2.

delta.m schrieb:1) = kein Auftrieb.
2) und 3) auch kein Auftrieb oder doch?

1 keine hebende Komponente, der Fall ist klar.

Falls 2 und 3 nicht maßstäblich gezeichnet wären könnte
man ein hübsches Gedankenexperiment machen :

Man verlängere den Körper so dass sich die untere Stirnfläche
am Grund und die obere an der (Wasser)Oberfläche befindet.

Dann würden beide Fälle eine hebende Kräftebilanz aufweisen,
da der Druck an der oberen Stirnfläche null ist ( Atmosphärendruck
mal vernachlässigt).

Ob die Körper schwimmen hängt dann vom
Dichteunterschied Körper/Fluid und Durchmesserverhältnis
untere Stirnfläche zum Körperdurchmesser ab (nehme obige
Körper Kraft eigener Willkür mal als zylinderförmig an).

@delta.m:

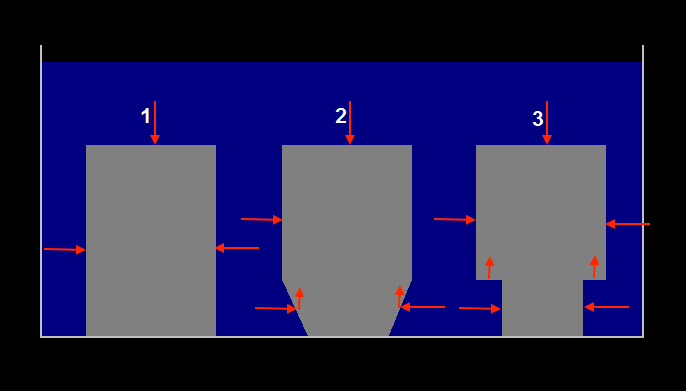
delta.m schrieb:1) = kein Auftrieb.
2) und 3) auch kein Auftrieb oder doch?

Sofern man den Begriff "Auftrieb" in physikalischem Sinne interpretiert, haben die Objekte 2 und 3 Auftrieb. Sobald es eine Fläche gibt, an der der Wasserdruck "von unten" angreifen kann, entsteht Auftrieb. Interpretiert man den Begriff "Auftrieb" umgangssprachlich in dem Sinne, ob ein Objekt schwimmt, hängt das natürlich von den konkreten Gegebenheiten ab (u.a. Dichte des Fluids und des Objekts) ab.

Ich möchte an dieser Stelle den Zusammenhang erläutern, warum Auftrieb im Standardfall anhand des Volumens eines Objekts berechnet werden kann, obwohl er ursächlich durch Druck auf die Flächen entsteht. Dazu sei der einfache Fall eines Objekts mit in Bezug auf die Hochachse konstantem Querschnitt betrachtet (z.B. ein Quader oder Zylinder). Für das Volumen eines solchen Objekts gilt:

V = A * h

Für den absoluten Wasserdruck in einer bestimmten Tiefe gilt (da der normalerweise für die Wassertiefe übliche Buchstabe h schon belegt ist, verwende ich anstelle dessen s, entsprechend der Strecke von der Wasseroberfläche bis zur jeweiligen Wassertiefe):

p = p_atm + rho_wasser * g * s

Für die Kräfte, die der Wasserdruck auf die obere und untere Querschnittsfläche des Objekts ausübt, gilt dementsprechend (beide Kräfte als positiv betrachtet):

F_oben = A * p_oben = A * (p_atm + rho_wasser * g * s_oben)

F_unten = A * p_unten = A * (p_atm + rho_wasser * g * s_unten)

Für die Auftriebskraft folgt daraus:

F_auftrieb = F_unten - F_oben = A * ((p_atm + rho_wasser * g * s_unten) - (p_atm + rho_wasser * g * s_oben))

Vereinfachen ergibt:

F_auftrieb = A * rho_wasser * g * (s_unten - s_oben)

Die Differenz s_unten - s_oben entspricht der Höhe h des Objekts, die multipliziert mit der Fläche A dem Volumen V entspricht. Daher gilt:

F_auftrieb = V * rho_wasser * g

Man könnte also in gewissem Sinne sagen, dass sich die Abhängigkeit des Auftriebs vom Volumen nur "zufällig" aus der Kraftwirkung des Wasserdrucks auf die Flächen ergibt. Für komplexer geformte Körper wird die Rechnung komplizierter, am Prinzip ändert sich jedoch nichts.

uatu schrieb:Ich möchte an dieser Stelle den Zusammenhang erläutern,

Ich hatte es geahnt. Da ich mir sicher war das uatu schneller ist
habe ich den Formeleditor von LibreOffice gar nicht erst bemüht.

Gut gemacht👍

@uatu

Vielen Dank für deine ausführliche Erklärung.

Etwas ist mir aber bei diesem Satz immer noch nicht ganz klar:

uatu schrieb:Sobald es eine Fläche gibt, an der der Wasserdruck "von unten" angreifen kann, entsteht Auftrieb.

Nochmals von mir eine Zeichnung dazu mit modifiziertem Objekt 3a) :



Das Objekt soll wieder einen luftgefüllten Zylinder darstellen, der plan unten aufliegt.
Es gibt hier also eine Fläche A1), an der der Wasserdruck "von unten" angreifen kann (mit Richtung nach oben).
Unterhalb gibt es jedoch nochmals eine Fläche A2), an der ebenfalls der Wasserdruck angreifen kann - diesmal Richtung nach unten.

Da der Druck auf A2) > A1) ist, sollte der Körper in diesem Fall nicht aufsteigen.

Ist das richtig?

Der Löwenanteil ist die fehlende hebende Komponente
an der unteren Stirnfläche.
Der Zylinder bleibt deswegen unten.

@delta.m: Zunächst kurz zu einem Punkt am Rande:

... nicht aufsteigen.

Man muss physikalisch streng zwischen der Auftriebskraft und der effektiv vertikal auf das Objekt wirkenden Kraft unterscheiden. Die effektiv vertikal auf das Objekt wirkende Kraft ergibt sich aus der Differenz zwischen der Auftriebskraft und der Gewichtskraft (F = m * g). Ist die Auftriebskraft grösser als die Gewichtskraft, steigt das Objekt auf, ist sie kleiner, sinkt es. Es kann also durchaus sein, dass eine erhebliche Auftriebskraft vorhanden ist, und das Objekt trotzdem sinkt (weil die Auftriebskraft kleiner als die Gewichtskraft ist).

Mal einfacher:
Ein Körper der perfekt am Boden des Beckens liegt ist ein "Saugnapf" - der hat auch keine Kraftkomponenten von unten.

@uatu
Ich bin echt erstaunt.
Da dachte man immer ganz lapidar bei gewissen Obejkte „Ja, schwimmt halt nach oben, weil die Luft es nach oben drückt.“
Jetzt öffnet sich mir eine ganz neue komplexe Welt und ich muss mir selber ein Facepalm geben. Ist mal wieder sehr erkenntnisreich :-)

Nun leuchtet mir die Tauchglocke noch mehr ein, also warum sie überhaupt absinkt so lange man sie absolut in Waage hält.

Mal ne blöde Frage: In einem früheren Leben habe ich mal den ehrenwerten Beruf eines Werkzeugmachers erlernt, und da hatten wir immer solche Endmaßkästen...



...die wir, wenn es nach unserem Lehrmeister ging, mit unserem Leben verteidigen mussten :D

Naja, egal, wenn man 2 dieser Endmaße aneinanderdrückte und gegeneinander verschob (wir sagten immer "ansprengen" dazu), waren beide Teile quasi wie verschweißt, und nur schwer voneinander zu trennen. Kann es sein, dass dieser Effekt etwas damit zu tun hat, dass die Luft zwischen den Endmaßen keine Angriffsfläche mehr hat, und beide Teile nun vom äußeren Luftdruck aneinandergepresst werden?

Wenn dem so wäre, dann würde mein Respekt gegenüber dem Luftdruck eine rapide Steigerung erfahren ... :D

skagerak schrieb:Da dachte man immer ganz lapidar bei gewissen Obejkte „Ja, schwimmt halt nach oben, weil die Luft es nach oben drückt.“

Man hat oft falsche oder unvollständige Vorstellungen von alltäglichen Phänomenen. Der erwähnte Saugnapf zum Beispiel "saugt" gar nicht, sondern wird vom Luftdruck auf die Fläche gedrückt, auf der sitzt. Ich benutze ab und zu solche "Sauger" zum Glas tragen, dabei ist es interessant sich vorzustellen, wie die Luft die Gummiflächen auf die Scheibe presst.